Ramanathan Sh. (Ed.) Thin Film Metal-Oxides: Fundamentals and Applications in Electronics and Energy

Подождите немного. Документ загружается.

78 D. Ruzmetov and S. Ramanathan

In Fig. 2.18, the peaks near 1 eV, above the O-2p peak are due to the V-3d bands

[16,50,60,67]. We see qualitatively the same behavior of the spectra as was reported

for bulk VO

with photon excitation of 21 eV [68] – a peak around 1 eV present in

both metallic and insulating phases and a weaker satellite appearing at the Fermi

level in the metallic VO

– with the difference that in our data the peaks are con-

siderably better resolved. The latter allows us to extract the precise peak positions

and widths by ﬁtting to the measured data. The line shape of each peak employed

in the ﬁtting is a numerical convolution of a Lorentzian with a Gaussian where the

latter represents the broadening due to the experimental instrument function. The

calculated spectra are shown in Fig. 2.18b by solid lines. The O-2p shoulder was

taken into account as an extra peak in the ﬁtting, so, for example, the metallic phase

was ﬁtted with an algebraic sum of three component peaks and a linear background.

The extracted peak parameters are discussed below: the single V-3d peak in the in-

sulating phase is located at 1.2 eV with linewidth of 1.0 eV. In the metallic phase the

doublet peak locations are 0.23 and 1.25 eV, linewidths being 0.76 and 1.5eV.

Photoemission studies on bulk VO

have shown well-resolved V-3d structure

with an unusual feature that the spectral weight was shifted mainly on the ﬁrst peak

(at E

) in the metallic phase [50]. Such spectral weight ratio agreed with the calcu-

lations by Biermann et al. based on cluster dynamical mean ﬁeld theory (CDMFT)

[50, 51]. In the spectra in Fig. 2.18, however, we see an opposite spectral weight

ratio, i.e., the peak at E

is at least three times less intense than the lower peak at

1.25 eV. It has been shown by Eguchi et al. that this ratio depends on the incident

photon energy [69], i.e., higher photon energies provide bulk sensitivity and the

spectra demonstrate higher DOS at the Fermi level. It is thus possible that the V-3d

spectra might be inﬂuenced by near-surface effects of the VO

ﬁlm. Nevertheless,

the fact that we clearly see the closure of the band gap upon MIT in Fig. 2.18b

strongly suggests that the presented spectra describe the valence band structure of

2.7 Optical Properties

Sharp changes of the electrical properties of VO

upon the MIT are accompanied

with the abrupt changes in the optical properties. Below we show the evolution of

the reﬂectance dispersion curves across the MIT and relate the changes of the optical

properties to electrical parameters. We demonstrate that the jump of the reﬂectivity

at the MIT can be as high as 92% (from 2 to 94%) at certain wavelengths.

Figure 2.19a shows the electrical resistance plot from a thin ﬁlm VO

sample.

The resistance change is over 4 orders of magnitude comparable to the sharpest

reported MIT in single crystals [7] and epitaxial ﬁlms [9]. The point of the highest

gradient of this log R curve is usually taken to deﬁne the MIT temperature, T

MIT

Fig. 2.19b shows the derivative of log R curve, d.log R/=dT , ﬁtted with a Gaussian.

The center and width of the Gaussian are 71 and 6

C, respectively, and correspond

to conventionally deﬁned T

MIT

and transition width 

MIT

, respectively.

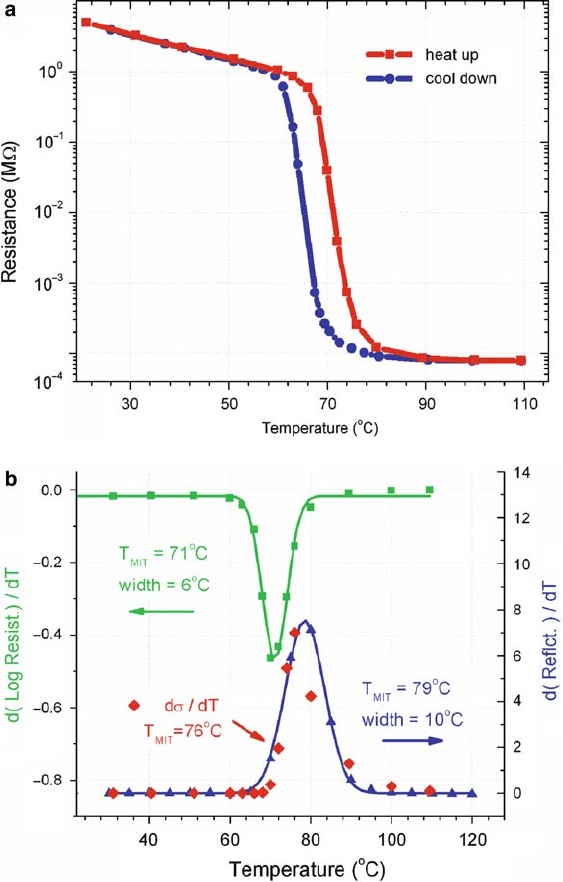
2 Metal-Insulator Transition in Thin Film Vanadium Dioxide 79

Fig. 2.19 Hundred-nanometer-thick VO

ﬁlm on Al

substrate. (a) Electrical resistance .R/;

(b) Green squares and solid line connecting them – the temperature derivative of log R during

heating shown in (a) and a Gaussian ﬁt to the data; red diamonds the derivative of the conductivity

.1=R/ corresponding to heating data in (a) on a linear scale; blue triangles the derivative of the

reﬂectance of 0.13 eV photons from Fig. 2.20b, blue line Gaussian ﬁt. (From Ruzmetov et al. [16]

with permission. Copyright (2008) by the IOP Publishing Ltd)

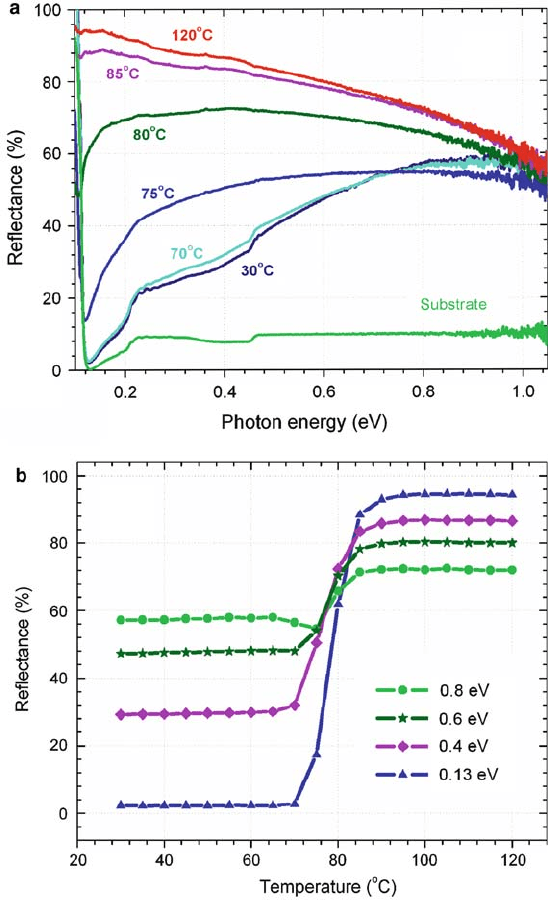
80 D. Ruzmetov and S. Ramanathan

Fig. 2.20 (a) Infrared reﬂectance taken from VO

ﬁlm as a function of incident photon energy

at different temperatures; (b) Reﬂectance change upon heating at selected photon energies. (From

Ruzmetov et al. [16] with permission. Copyright (2008) by the IOP Publishing Ltd)

The mid-infrared reﬂectance spectra from a VO

ﬁlm on c-plane Al

substrate

are shown in Fig. 2.20. These optical measurements were done on the same ﬁlm

whose electrical transition is shown in Fig. 2.19 allowing a direct comparison

2 Metal-Insulator Transition in Thin Film Vanadium Dioxide 81

between electrical and optical data [16]. The temperature dependence of reﬂectance

at selected incident photon energies is shown in Fig. 2.20b. One can see a sharp

increase in reﬂectance when the ﬁlm is heated across the metal–insulator transition.

Larger magnitude of the reﬂectance switching occurs at lower photon energies. For

example, at h D 0:13 eV. D 9:54 m/ the reﬂectance switches from 2 to 94%

upon the MIT, which well exceeds the largest reported magnitudes of optical re-

ﬂectance and transmittance switching in this material [4, 70–72]. One can see from

Fig. 2.20a that most of the change in the spectra with temperature occurs within

C interval including the transition temperature. The magnitude of the switch-

ing seen in Fig. 2.20b is monotonically decreasing with increasing photon energy,

while the transition interval remains the same 15

C. The sharp slopes at MIT and

the ﬂat portion of the curves below and above the transition are potentially valuable

for developing applications such as optical switches.

An interesting feature is observed in the 0.8 eV reﬂectance curve in Fig. 2.20b.

There is a distinct decrease of the reﬂectance at the onset of MIT near 75

C. This

feature is also seen in the spectra in Fig. 2.20a. The 75

C curve is lower than

C in the energy interval from 0.75 up to 1 eV. It is worthwhile to note that the

value of the band gap in semiconducting (monoclinic lattice) VO

is 0:6–0:7 eV

[60, 64]. The inelastic scattering involving excitations across the band gap become

possible in the h range 0.75–1eV where a decrease in reﬂectance is observed.

However this may not directly explain the temperature dependence of the effect,

i.e., its appearance right near the T

MIT

. More likely, this phenomenon may be sim-

ilar to the critical opalescence in liquid–vapor phase transitions. It has been shown

that the semiconductor-to-metal phase transition in VO

occurs percolatively: ﬁrst

metallic puddles nucleate, then their size grows until the metallic phase percolates

throughout the whole material [58, 70]. During the transition, there is coexistence

of spatially separate metallic and insulating phases. When the wavelength of the in-

cident radiation is comparable with the characteristic size of the metallic puddles,

enhanced scattering is expected which would lead to the decline in reﬂection. The

typical size of the metallic puddles in the middle of the transition can be estimated

to be 1–2m[58]. Further growth of the metallic puddles results in complete merg-

ing of the metallic phase and consequently an increase of the reﬂectance. Enhanced

scattering is then expected at  D 1–2m .PE D 1:2  0:6 eV/ in agreement with

our observation.

Another interesting feature can be noted from a comparison of the electrical and

optical MIT characteristics shown in Fig. 2.19b. The derivative of the reﬂectance

is ﬁtted with a Gaussian to determine the optical transition temperature and width.

If one assumes the MIT temperature to be the highest gradient point in the log of

resistance curve, then the T

MIT

would be equal to 71

C, which is 8

C apart from the

highest gradient point in the reﬂectance data, 79

C. The maximum error between the

sample temperature readings in electrical and optical experiments was determined

to be less than 2

C and cannot explain the mentioned 8

C difference. To understand

the origin of the discrepancy we have plotted in Fig. 2.19b the derivative of the

electrical conductance d=dT upon heating calculated from the data in Fig. 2.2a

. D 1=R/. We found that the point of highest gradient of the conductance, 76

82 D. Ruzmetov and S. Ramanathan

is closer to the optical transition point, 79

C, and, more importantly, that the interval

of the conductance change overlaps with the interval of the optical transition. The

latter indicates that the ﬁlm’s optical characteristics can be better described as a

direct function of conductance, or consequently the free carrier density, and the

center of the reﬂectance transition occurs at the threshold conductance value close

to the highest gradient of .T/.

The remarkably large switching of the optical properties described above, the

fact that the material is in thin ﬁlm form, which can potentially be integrated into

electronic and optical devices, and relatively simple way of the synthesis of our

polycrystalline ﬁlms (DC sputtering as opposed to epitaxial methods of ﬁlm growth)

make these results to be of potential signiﬁcance to switching technologies.

2.8 Magneto-Transport

As it is discussed in Sect. 5, there are a number of theoretical models developed

describing MIT in VO

. The carrier density is a critical parameter in some of those

models (e.g., Mott theory [37]) and is an important reference parameter in the oth-

ers (e.g., for comparison with the predictions of the electronic occupancies of the

molecular orbitals). The knowledge of the carrier density across MIT is important

in order to distinguish between competing theories and understand the origin of the

phase transition.

Early Hall effect measurements in VO

showed that electrons were predominant

carriers on the both sides of the MIT [66, 73–76]. The values of the electron den-

sity reported by research groups could differ by 2 orders of magnitude both in the

semiconducting phase at room temperature [66, 73, 75] and high-T metallic phase

[73, 75]. As mentioned in the literature [66, 77], the Hall effect measurements in

is a challenging task due to the following difﬁculties: low Hall mobility, high

carrier density resulting in low Hall voltage, and unusually large amount of noise

ascribed to be due to the strain present in the sample arising from the discontinu-

ous lattice transformation at the structural phase transition (SPT). Carrier density

determination in high-quality vanadium oxide ﬁlms is important, given the recent

interest in exploiting the Mott transition for computational elements that may over-

come limitations due to Si CMOS scaling [78].

We now discuss recent results on Hall and magnetoresistance measurements in

thin ﬁlm VO

in DC magnetic ﬁeld of up to 12T [77]. The temperature depen-

dence of the electrical resistivity, carrier density, and Hall mobility across the MIT

is shown below. The measured n-type conductance in the semiconducting phase is

consistent with recent photoemission spectroscopy results [16]. The novelty and im-

portance of these results are that the high ﬁeld measurement technique allowed for

reliable Hall coefﬁcient determination in both semiconducting and metallic states of

high quality thin ﬁlm VO

ﬁlm (100-nm thick) on a sapphire substrate was photo-lithographically pat-

terned into a clover-leaf shape for van der Pauw measurements (Fig. 2.21a) [77].

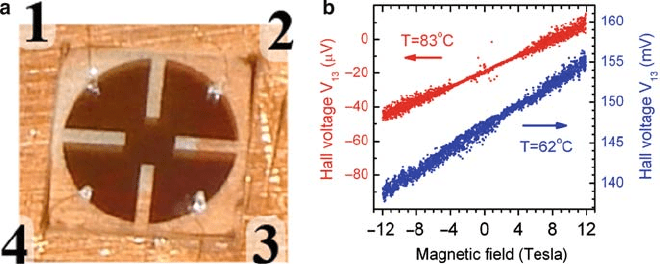
2 Metal-Insulator Transition in Thin Film Vanadium Dioxide 83

Fig. 2.21 (a)VO

sample mounted on a copper base and set up for Hall measurements. Dark

clover-leaf pattern is a VO

ﬁlm on transparent square sapphire substrate of 1 cm  1 cm size.

(b) The Hall voltage V

in the metallic (upper red dot group) and semiconducting (lower blue

dot group) state. (From Ruzmetov et al. [77] with permission. Copyright (2009) by the American

Physical Society)

The sample was silver paste mounted on a copper block equipped with a resistive

heater. This custom made setup with LakeShore 340 temperature controller insured

sample temperature stability within 0:05

C, which proved to be a necessary require-

ment since the sample resistance exponentially varied with temperature. Gold wires

were indium-soldered to the sample. Another wiring method where a second layer

of photo-lithography was used to connect 15-m-wide thin ﬁlm gold leads to the

pattern yielded similar results. Electrical measurements on the sample were

done with a DC current source and voltmeter. The copper block with the sample was

placed inside a room temperature bore of a 14T cryogen-free magnet. Constant cur-

rent I

was set through the sample. The current magnitude was set to maximum

before the current heating effects became present and varied from 35 Aat33

Cto

120 Aat64

C in the semiconducting phase and up to 10 mA in the metallic phase.

Hall voltage V

was measured while the magnetic ﬁeld was continuously ramped

0 ! 12T !12T ! 0 at a preset temperature. The resistivity was measured

by van der Pauw method and calculated by solving numerically the transcendental

equation (1) in [79].

In the magneto-transport measurements on the 12T apparatus [77], the tempera-

ture was incrementally increased through the MIT. An example of the Hall voltage

curves in semiconducting and metallic phases is shown in Fig. 2.21b. Hall re-

sults are interpreted within a single band model, so that the slopes of the V

.B/

curves were used to extract Hall carrier densities using the equation (SI units):

n D IB=.V

ed/,whereI D I

is the current through the sample, B – magnetic

ﬂux density directed perpendicular to the sample plane, V

D V

– Hall voltage,

e D 1:60  10

19

C;dD 10

7

m – ﬁlm thickness. The measured resistivity and

carrier density for the thin ﬁlm VO

sample are presented in Fig. 2.22.

The resistivity experiences a drop of over 3 orders of magnitude at the transition

temperature T

MIT

D 70

C, which is characteristic to vanadium dioxide. Together

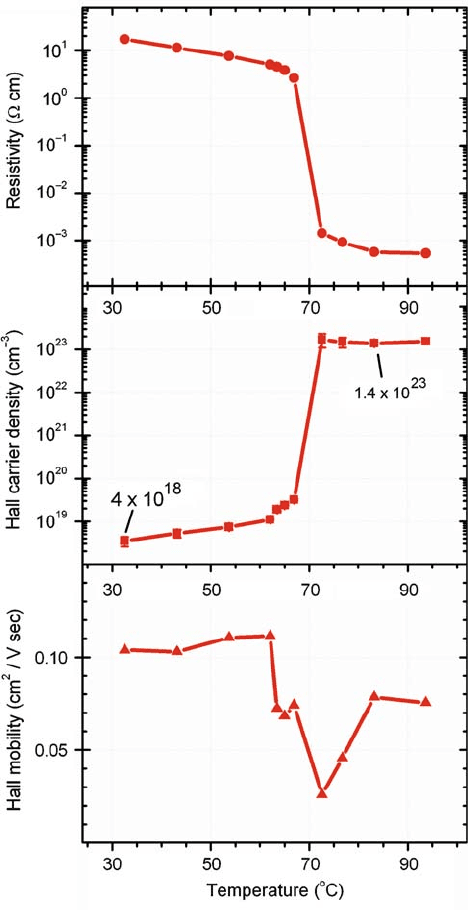
84 D. Ruzmetov and S. Ramanathan

Fig. 2.22 Electron transport properties of a thin ﬁlm VO

on an Al

substrate measured by

12T sweeping ﬁeld apparatus. The Hall coefﬁcient sign corresponds to electrons as the dominant

current carriers. (From Ruzmetov et al. [77] with permission. Copyright (2009) by the American

Physical Society)

2 Metal-Insulator Transition in Thin Film Vanadium Dioxide 85

with the results of the X-ray diffraction analysis [77] this demonstrates the high

quality and stoichiometry of the synthesized VO

ﬁlms. The mobility  D 1=.e n /

was determined from known resistivity  and carrier density n andplottedinthe

bottom panel of Fig. 2.22. Positive magnetoresistance, i.e., a resistance increase

upon application of magnetic ﬁeld, was measured in the semiconducting phase at

room temperature. Speciﬁcally, the magnetoresistance is R=R D .0:09 ˙0:02/%

in the ˙12Tﬁeldat26

C, where R D V

(in notations of Fig. 2.21a).

One can see in Fig. 2.22 that the Hall electron density increases by 4 orders of

magnitude from 1:1 10

3

at 64

Cto1:7 10

3

at 75

C upon the MIT.

The increase of the number of carriers accounts almost entirely for the decrease of

electrical resistance, which is also manifested in the small change in the mobility .

The fact that in the Hall measurements there appear to be more than one itinerant

carrier per V ion may be explained by the presence of two types of conduction,

n- and p-type, with electrons being the majority carriers [12].

2.9 Devices

More evidence is emerging ascribing the metal–insulator transition in VO

to be

a Mott transition [37]. In the Mott picture, the insulating state is achieved due to

the correlations between itinerant carriers [80]. The free carrier density is a key pa-

rameter that, upon the change of some external parameter such as temperature or

electric ﬁeld, increases to a certain critical value causing the transition to metallic

state. Once the Coulomb repulsion between the electrons is overcome, further in-

crease of the carrier density occurs continuously. The fact that the MIT is activated

by the carrier density makes these materials promising for applications. The carrier

density in conventional semiconductors can be readily manipulated, for example,

by means of electric ﬁeld or photo-excitation. There are a number of device con-

ﬁgurations allowing efﬁcient carrier density control in a semiconductor channel that

are already being utilized in modern electronics. Making use of those conﬁgurations

and device schemes to develop devices that show explicitly that the MIT in VO

can

be induced solely by means of carrier density manipulation is a big challenge on the

way toward incorporating VO

materials in novel applications in electronics.

It has been found by a number of researchers that the application of sufﬁciently

high voltage across a two-terminal VO

device induces a metal–insulator transition

even if the sample is kept at room temperature [57, 81–83]. In early reports [81],

the MIT switching was explained by the Joule heating of the VO

material over the

MIT

by the current ﬂowing through the two-terminal device. In some recent reports,

the switching is argued to be due to the electric ﬁeld (not thermally)-induced MIT

in accordance to the Mott theory [83].

B.-J. Kim et al. performed electrical measurements on two-terminal VO

de-

vices consisting of a thin (100 nm) ﬁlm VO

stripe contacted with Ni electrodes

on both sides [84]. The device dimensions are shown in the inset of Fig. 2.23.In

the experiments of B.-J. Kim et al. [84], the temperature dependence of the current

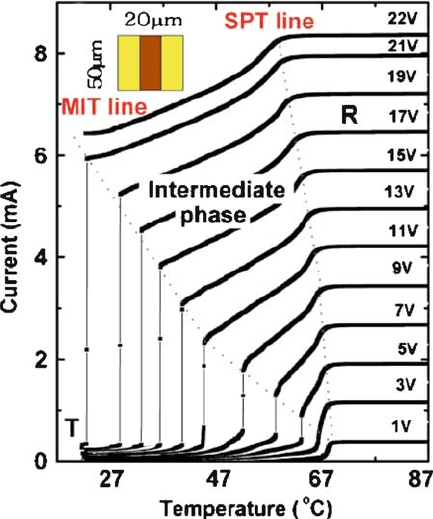
86 D. Ruzmetov and S. Ramanathan

Fig. 2.23 The temperature dependence of a current through a two-terminal VO

device (inset)

at different applied voltages. At higher applied voltages the current jump corresponding to MIT

shifts to lower temperatures. (From Kim et al. [84] with permission. Copyright (2007) by American

Institute of Physics)

through the device was measured at different applied voltages ranging from 1 to

22 V (Fig. 2.23). At a small applied voltage of 1 V, a jump in the current due to

MIT is observed near 67

C, which is close to the conventional MIT temperature in

single crystal (T

MIT

D 68

C[12]) and thin ﬁlm VO

MIT

D 71

C, see Fig. 2.19).

At higher applied voltages the current jump occurs at lower temperatures. This ef-

fect is explained by an electric ﬁeld-induced metal–insulator transition (MIT): the

electric ﬁeld produced by an applied voltage favors the MIT so that at higher volt-

ages lower temperature is sufﬁcient to trigger the phase transition [84]. According

to B.-J Kim et al., the ﬁeld-assisted transition to metallic state is not necessarily ac-

companied by the structural phase transition (SPT), i.e., lattice transformation from

monoclinic to tetragonal structure. So that there is an intermediate metallic phase,

which remains to have monoclinic lattice. The current in this intermediate phase

continues to increase with temperature at constant applied voltage until the SPT

occurs. The temperature increase beyond SPT results in almost constant saturated

current, which allows delimiting the boundaries of all three phases in the graph

of Fig. 2.23: monoclinic semiconductor phase, monoclinic metallic (intermediate

phase), and tetragonal metallic phase. Further arguments in favor of the intermediate

phase and the separation of MIT and SPT can be found elsewhere [37].

2 Metal-Insulator Transition in Thin Film Vanadium Dioxide 87

One needs to consider carefully the electric ﬁeld-induced MIT in two-terminal

devices. The current that passes through the device causes Joule heating that can

raise the temperature of VO

toward T

MIT

. The latter would result in conventional

temperature activated MIT rather than ﬁeld induced one. If there is nonuniform con-

ductance in the VO

ﬁlm, then the applied voltage may raise the temperature of VO

in a narrow ﬁlament of the material causing thermal MIT in the ﬁlament. The rest of

the ﬁlm that does not participate in conduction will remain at low temperature. In or-

der to eliminate the possibility of this and similar scenarios more experiments need

to be considered. Three-terminal devices are especially of interest since an electric

ﬁeld induced by the third terminal (gate) causes only minimal leakage current and,

consequently, heating.

There are only a few reports on the measurements of three-terminal VO

devices

consisting of a source, drain, and gate [57, 85]. The application of an electric ﬁeld

in VO

through a gate seems to shift the critical source–drain ﬁeld that induces the

MIT. However, the interpretation of the ﬁeld effect is complicated by the fact that the

same polarity of the gate voltage may either increase or decrease the critical source–

drain ﬁeld [57]. Careful studied of three-terminal VO

devices are still desirable in

order to clarify the effect of the electric ﬁeld induced by a gate on the transport

properties of VO

There have been attempts to discriminate heating and ﬁeld effects in two-terminal

devices by means of time-resolved measurements. The switching time of the MIT

was measured and arguments were given that thermally activated switching would

occur at a slower rate than it was observed leaving the electric ﬁeld induced MIT as

the mechanism of the phase transition [86].

Another important type of VO

devices to be studied is two-terminal devices

with the C urrent ﬂowing P erpendicular to sample P lane (CPP geometry) as op-

posed to in-plane devices (Current InsamplePlane or CIP geometry) described in

Fig. 2.23. Ko et al. performed experiments comparing electron transport in CPP and

CIP geometries and demonstrated that the MIT can be induced by application of

electric ﬁeld across a thin VO

ﬁlm [87]. Experiments on devices in CPP conﬁgu-

ration are important from the scientiﬁc point of view since MIT in VO

is probed

on the nanoscale that is equivalent to the thickness of the VO

thin ﬁlm. Also CPP

devices are attractive from the perspective of potential applications in electronics

because CPP geometry allows high device density.

In the experiments of Ko et al. [87] palladium electrodes (0:5 mm  0:5 mm

squares, 200-nm thick) were placed on top of a 150-nm thick VO

ﬁlm deposited

on a conductive silicon substrate. The latter was used as the bottom electrode, so

that a voltage was applied across the thickness of the ﬁlm and the current was mea-

sured (Fig. 2.24). The current curves at temperatures below 55

C feature jumps near

2 V bias could be due to the electric ﬁeld assisted MIT (E-MIT). An abrupt current

change in Fig. 2.24 seen in the direction of a constant voltage (e.g., 0.6 V) between

70 and 75

C curves corresponds to a conventional thermally induced MIT (T-MIT).

The convergenceof the high .T > T

MIT

 70

C/ and low temperature curves at high

ﬁelds indicate that both effects, T-MIT and E-MIT, produce the transition to a similar

metallic phase of the VO

material. This conclusion makes alternative explanations