Раинкина Л.Н. Гидромеханические расчеты трубопроводных систем с насосной подачей жидкости
Подождите немного. Документ загружается.


Глава 4. Расчеты на прочность элементов гидравлической сети 51
Иллюстрация к определению разрывающих сил
На выделенные объемы жидкости
действуют:
1. Реакции со стороны поверхностей
R
i
(они равны по модулю и противо-
положны по направлению искомым
силам давления
Р
i
).
2. Силы давления N
i
со стороны от-
брошенных частей жидкости.
3. Вес выделенных объемов.
Рис.32.
Учитывая, что силы давления
Р
i
равны произведению давления на соответ-
ствующие площади сечений, и весом жидкости
G
i
можно пренебречь вследствие
его малости по сравнению с другими силами, из уравнений равновесия
N
i
= R
i
по-
лучим:
“a”
PR p
D
11
2
4
==⋅
⋅
π
;
“б”
PR p
D
PR plD
D
11
2
22
2
44
==⋅
⋅
==⋅⋅+
⋅
ππ
;();
(62)
“в”
P R p hD ghhD p
м11 0
0=
=
⋅⋅
=
⋅
⋅
⋅
⋅
≈
max
;
ρ
().
Для схемы "в" сила
P определяется по ожидаемому максимальному давле-
нию.
Сила сопротивления
F, возникающая в материале стенки, равна произведе-
нию напряжения
σ
на соответствующую площадь разрыва (ввиду симметрии ре-
зервуаров сечения, по которым происходит разрыв, равны изображенным на
Рис.31):
“a”
FD
1
=⋅
⋅
⋅
σ
π
δ
;
“б”
FDF lD
12
2=⋅⋅⋅
=
⋅
⋅
+
⋅
σ
π
δ
σ
δ
π
;();
(64)
“в”
FhD
1
22=⋅
⋅
+
σ
δ
();
Искомую минимальную толщину стенки определяем из равенства сил
P и F
при условии, что напряжения на разрыв равны допускаемым [
σ
]:
“а”
[]
δ
σ
min
=
⋅
⋅
pD
4
;

52
Гидромеханические расчеты трубопроводных систем
с насосной подачей жидкости
“б”
[] [] []
δ
σ
δ
π
σ
π
σ
12
22
4
4
2
4
2
4
min min
=
⋅
⋅
=
⋅⋅+
⋅
⋅⋅+
=
⋅⋅+
⋅
⋅
⋅⋅+
pD
plD
D
lD
pD l
D
lD
;
()
()
()
()
;
“в”
[]
δ
ρ
σ
min
=
⋅
⋅
⋅
⋅
⋅⋅+
ghhD
hD2 ()
;
(65)
Из (65"б") следует, что
δ
2 min
= 2
δ
1 min
, то есть наиболее опасным сечением
является сечение
2-2, и толщина стенки резервуара должна быть больше
δ
2 min
.
На практике расчетную толщину стенок резервуара увеличивают с учетом
запаса прочности на сварные швы.
Глава 5. Определение времени опорожнения резервуаров от жидкости 53
Глава 5
Определение
времени опорожнения
резервуаров от жидкости
Инженерные расчеты гидравлических систем включают в себя и определе-
ние параметров, характеризующих процесс наполнения (опорожнения) резервуа-
ров. Такими параметрами являются время наполнения (опорожнения), диаметр
отверстия или насадка и др.
Получим расчетные зависимости для анализа таких процессов.
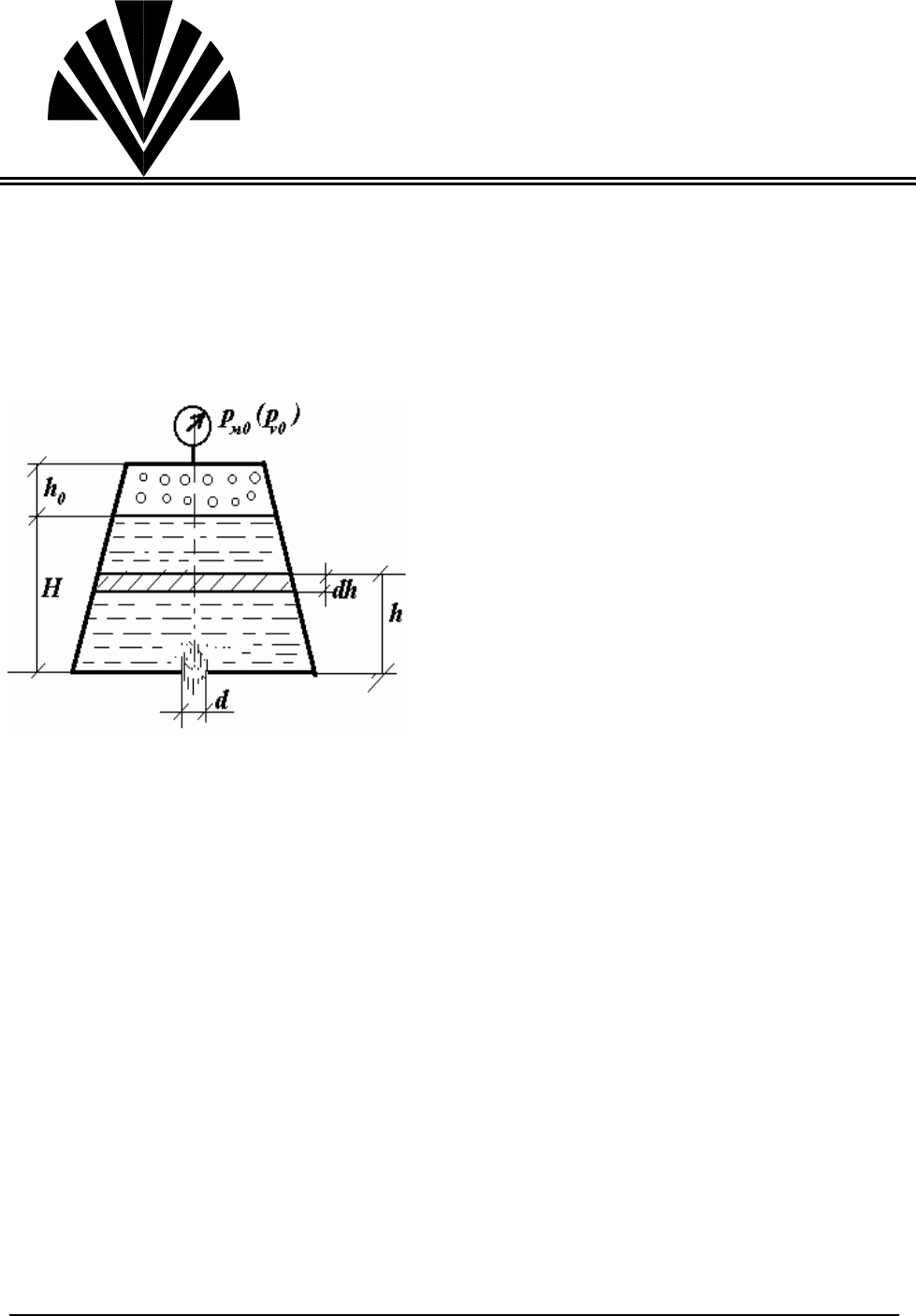
Расчетная схема
Жидкость плотностью
ρ
вытекает из
резервуара через отверстие диамет-
ром
d. К отверстию может быть при-
ставлен насадок любой формы. В об-
щем случае резервуар закрыт и над
жидкостью находится газ, давление
которого не равно атмосферному (по-
казание манометра равно
р
м0
или р
v0
).
Площадь поперечного сечения резер-
вуара меняется в зависимости от вы-
соты жидкости по произвольному за-
кону, т.е.
Ω
=
Ω
(h).
Рис.33.
При решении таких задач полное время истечения обычно разделяют на
бесконечно малые промежутки, в каждом из которых высоту
h считают постоян-
ной, а движение не зависящим от времени. Такой прием позволяет для каждого
бесконечно малого промежутка времени использовать законы для установившего-
ся движения жидкости. При этом получается дифференциальное уравнение, путем
интегрирования которого и определяется полное время истечения. Кстати, если
время задано, можно определить высоту
H или какой-нибудь другой параметр,
например, давление
p
oм
.
Пусть в некоторый промежуток времени уровень жидкости равен
h. К этому
моменту времени часть жидкости вытекла из резервуара, при этом объем газа уве-
личился, а его давление уменьшилось и стало равно
p(h). За время dt уровень
жидкости уменьшился на
dh, а объем жидкости уменьшился на величину dV = -
Ω
(h)
⋅
dh. В течение бесконечно малого промежутка времени dt можно считать рас-
ход жидкости через отверстие постоянным и равным:
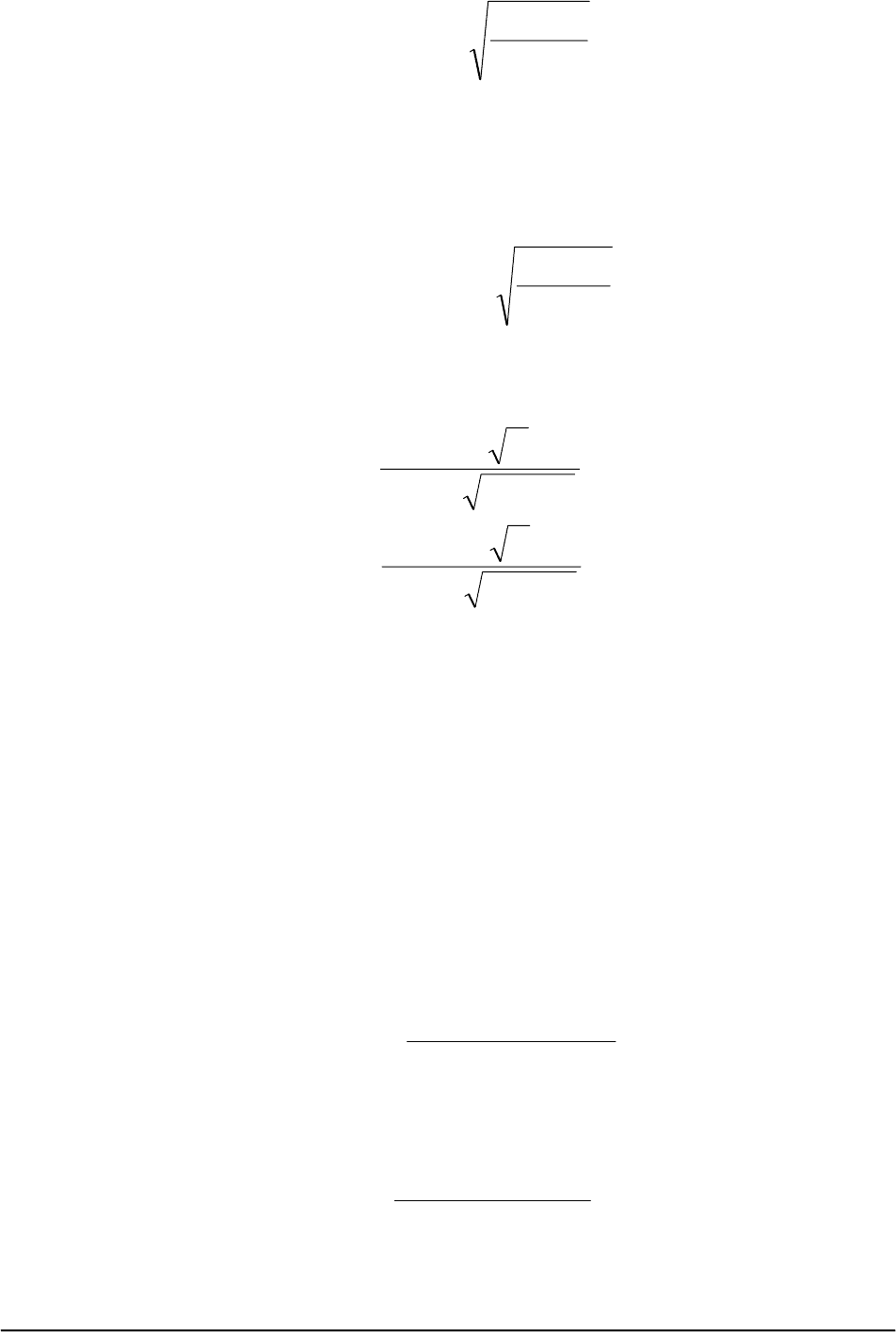
54
Гидромеханические расчеты трубопроводных систем
с насосной подачей жидкости
Q
ph
=⋅⋅
μω
ρ
2
Δ
()
,
где
ω
=
π⋅
d
2
/4 - площадь сечения отверстия,
μ
- коэффициент расхода отверстия, а
Δ
р(h) - перепад давления на отверстии.
За время
dt через отверстие вытекает объем жидкости, равный Qdt.
Приравнивая объемы, получим следующее дифференциальное уравнение:
−⋅=⋅⋅ ⋅
Ω
Δ
()
()
hdh
ph
dt
μω
ρ
2
.
Это уравнение с разделяющимися переменными. Для определения времени
истечения жидкости необходимо разделить переменные и взять интеграл от обеих
частей уравнения.
dt
hdh
ph
t
hdh
ph
=
−⋅⋅
⋅⋅
=
−⋅⋅
⋅⋅
∫
Ω
Δ
Ω
Δ
()
()
;
()
()
.
ρ
μω
ρ
μω
2
2
(66)
Для вычисления интеграла (66) необходимо раскрыть функции
Ω(
h) и
Δ
p(h)
в конкретной задаче и вычислить значение верхнего предела. При этом следует
руководствоваться следующим:
1. В процессе истечения жидкости газ расширяется по изотермическому за-
кону. Если давление газа в начальный момент больше атмосферного, уравнение
изменения состояния газа имеет вид:
(p
мо
+ p
ат
)
⋅
V
o
= p(h)
⋅
V(h)
(67)
Здесь V
o
- начальный объем газа, известная величина, а V(h) - объем газа в
момент времени
t. Конкретный вид функции V(h) зависит от формы сосуда.
Из уравнения (53) определяется давление газа в момент времени
t, то есть
при высоте жидкости
h:
ph
ppV
Vh
()
()
()
=
+
⋅
ат мо o
(68)
Если давление газа в начальный момент меньше атмосферного, давление в
момент времени
t определяется так:
ph
ppV
Vh
o
()
()
()
=
−
⋅
ат Vo
(69)
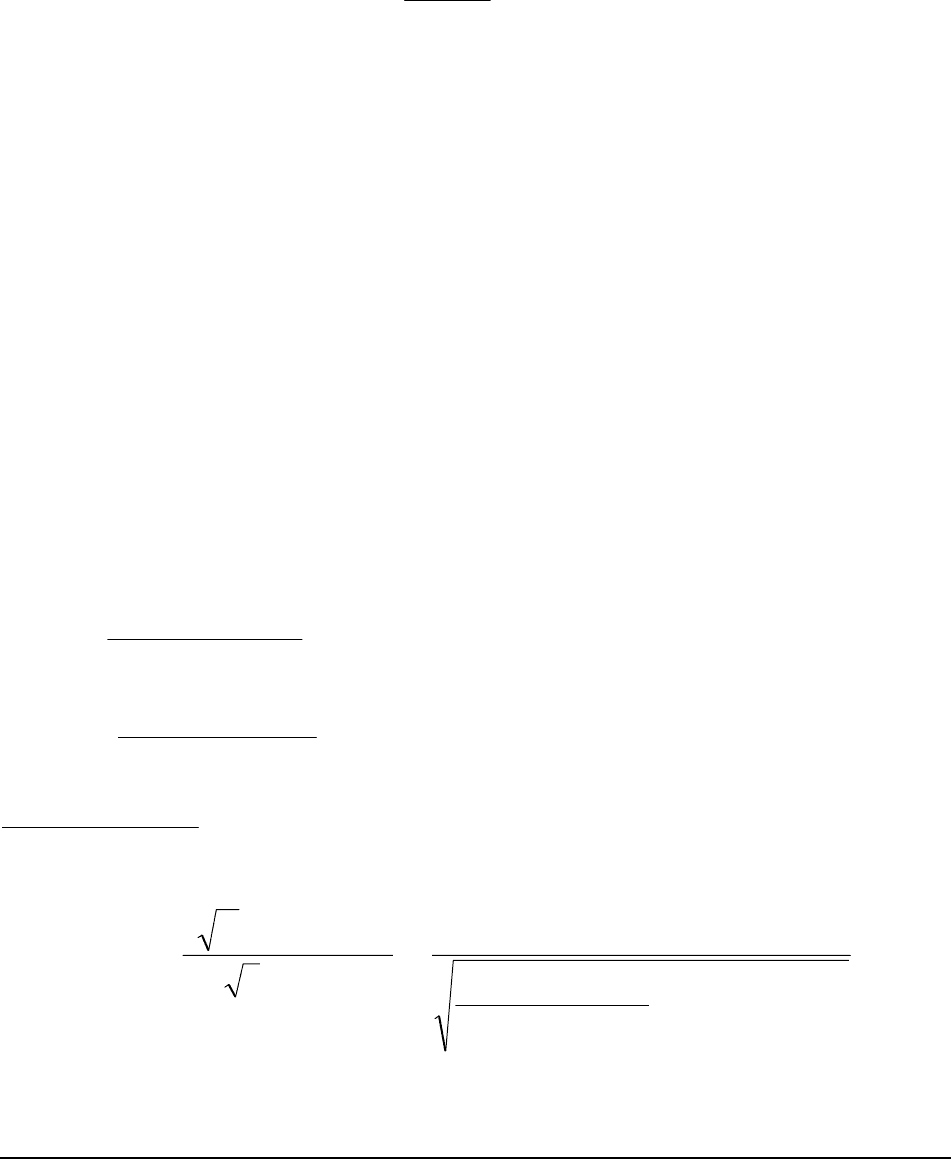
Глава 5. Определение времени опорожнения резервуаров от жидкости 55
2. Перепад давления
Δ
p(h) в момент времени t на отверстии равен разности
давлений на входе и на выходе из отверстия:
Δ
p(h)=p(h) +
ρ⋅
g
⋅
h - p
ат
3. Верхний предел при интегрировании определяется из условия, что пере-
пад давления
Δ
p(h
к
) равен нулю, и истечение прекращается. Для определения h
к
необходимо решить систему уравнений:
ph g h p
ph
pV
Vh
kk
k
oo
k
()
()
()
+
⋅
⋅
−
=
=
⋅
ρ
ат
0
(70)
Здесь
р
о
- начальное абсолютное давление газа.
р
о
= p
мо
+ p
ат
, если р
о >
p
ат
р
о
= p
ат
- p
vо
, если р
о <
p
ат
Из системы (70) определяется предельная высота жидкости h
k
, при которой
истечение прекращается.
4. Конкретный вид функции
Ω
(h) зависит от формы резервуара.
5. В большинстве практических случаев интеграл (66) не вычисляется в
квадратурах и его можно вычислить численно на ЭВМ.
Пример: резервуар цилиндрический, давление газа меньше атмо-
сферного,
D - диаметр цилиндра.
Ниже представлены все уравнения и зависимости, необходимые для реше-
ния задачи.
Ω
() /hDconst=⋅ =
π
2
4
- закон изменения площади
сечения по высоте
VDh
oo
=⋅ ⋅(/)
π
2
4
- начальный объем газа
ph
pph
Hh h
а o
o
()
()
=
−⋅
+−
т vo
- давление газа в момент вре-
мени
t.
Δ
ph
pph
Hh h
gh p
o
o
()
()
=
−⋅
+−
+⋅⋅−
ат vo
ат
ρ
- перепад давления на отвер-
стии в момент времени
t.
()pph
Hh h
gh p
o
o
ат vo
ат
−⋅
+−
+⋅⋅− =
ρ
0
- уравнение для оп-
ределения
h
k.
(71)
T
D
d
dh
pph
Hh h
gh p
o
o
а
H
h
k
=−
⋅⋅
⋅⋅⋅
⋅
−⋅
+−
+⋅⋅−
∫
ρπ
μπ
ρ
2
2
4
24
/
/
()
ат vo
т
;
- формула для определения времени истечения. (72)

56
Гидромеханические расчеты трубопроводных систем
с насосной подачей жидкости
Из уравнения (71) определяется верхний предел при интегрировании, а ин-
теграл (72) вычисляется численно (методом прямоугольников, трапеций и др.).
Перед вычислением уравнение (72) необходимо привести к безразмерному
виду. Для этого вводим характерное время
T
0
:
T
H
gH
0
2
=
⋅
⋅⋅ ⋅⋅
Ω
μω
(73)
По формуле (73) определяется время вытекания из открытого резервуара
площадью
Ω
объема жидкости высотой H через отверстие площадью
ω
при по-
стоянном уровне (в случае, когда в резервуар поступает такое же количество жид-
кости, что и вытекает).
Обозначим:
T/T
0
=T
безр.
; h/H=h
безр.
; h
к
/H=h
к.безр
; h
0
/H=h
0.безр
и разделим обе
части уравнения (72) на
T
0
. Тогда получим:
T
dh
pph
gH h h
h
p
gH
v
h
безр.
безр
ат безр.
0.безр. безр.
безр.
ат
к.безр
=−
−⋅
⋅⋅ ⋅ + −
+−
⋅⋅
∫
()
()
;
.00
1
1
ρρ
(74)
Перед вычислением интеграла (74) необходимо вычислить значение
верхнего предела
h
k
. В данном примере длл этого нужно решить квадратное
уравнение (71).
Применим для вычисления интеграла (74) формулу прямоугольников:
ydx h y y y
a
b
n
⋅=⋅ +++
∫
−
( ... )
01 1
Опуская индекс “безр.”, для нашей задачи имеем:
yx fhh
yfh
pph
gH h h
h
p
gH
xhah b h
ba
n
h
n
a
b
h
v
k
k
k
k
⋅=
==
−⋅
⋅⋅ ⋅ + −
+−
⋅⋅
====
−
=
−
∫∫
ΔΔ
ΔΔ Δ
() ;
()
()
()
;
;;; ;
1
00
1
1
1
ат ат
ρρ
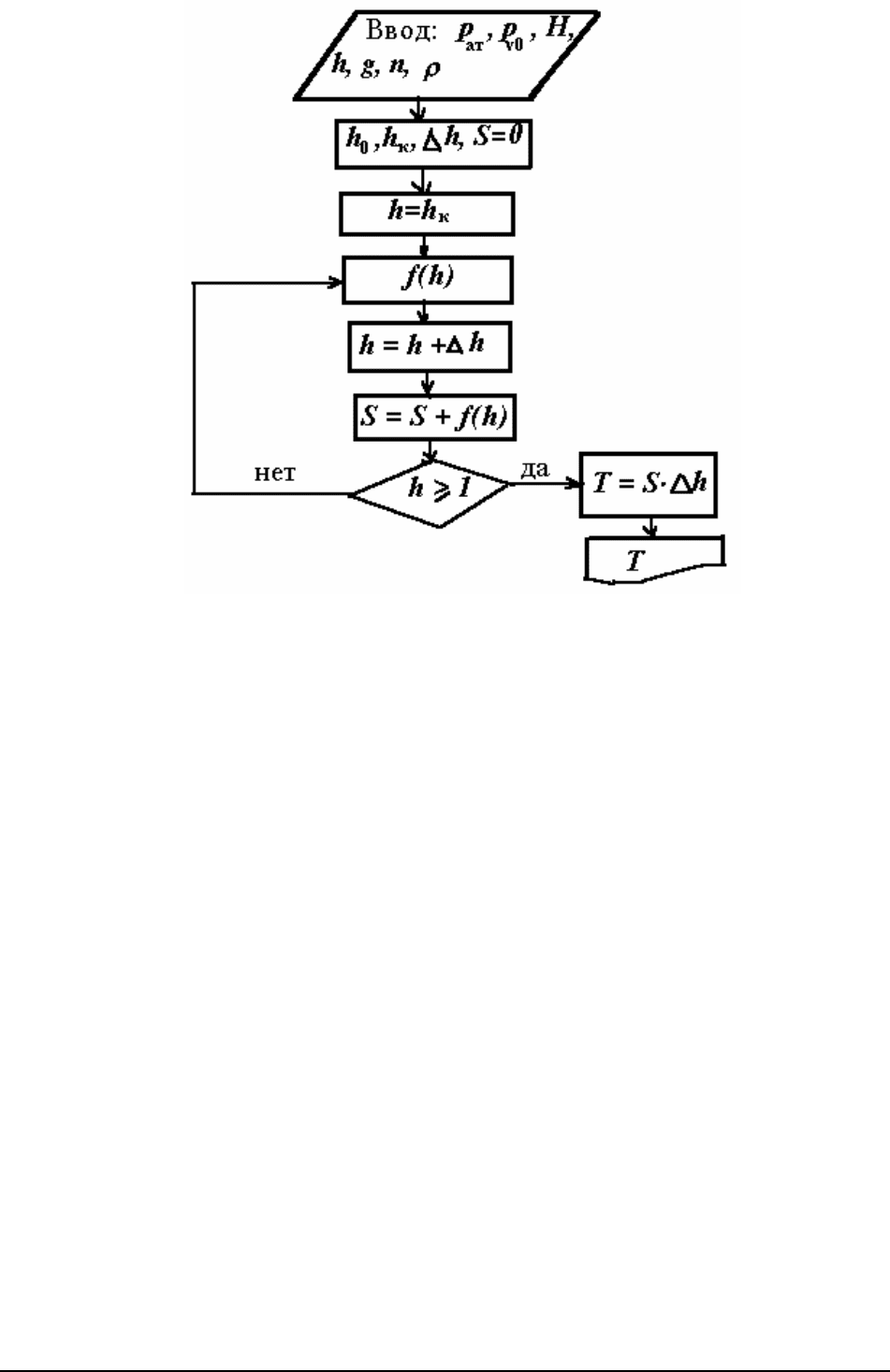
Блок-схема вычисления интеграла (74) по формуле прямоугольников
Глава 5. Определение времени опорожнения резервуаров от жидкости 57
Рис.34.

58
Гидромеханические расчеты трубопроводных систем
с насосной подачей жидкости
Глава 6
Рекомендации
по выполнению
курсовой работы
Для выполнения курсовой работы необходимы знания следующих
разделов курса "Гидромеханика":
l. Уравнение Бернулли для потока реальной несжимаемой жидкости.
2. Практическое применение уравнения Бернулли.
3. Два режима движения жидкости, число Рейнольдса.
4. Гидравлические сопротивления.
5. Гидравлический расчет простых и сложных трубопроводов.
6. Расчет всасывающей линии насосной установки. Насосная установка и ее
характеристика.
7. Работа насоса
на сеть.
8. Сущность кавитационных явлений.
9. Истечение жидкости через отверстия и насадки.
10. Неньютоновские жидкости.
11. Гидравлический удар в трубопроводе.
12. Определение давления в жидкости и силы давления жидкости на по-
верхность твердого тела.
Решение поставленной студенту задачи выполняется аналитически, часть
задачи, указанной преподавателем, рассчитывается при помощи ЭВМ.
Решение задачи связано
, главным образом, с нахождением рабочих па-
раметров системы "насосная станция (резервуар) — трубопровод" и измене-
нием параметров работы установки при подключении параллельных или по-
следовательно соединенных участков труб, а также при изменении характе-
ристик насоса.
При работе всасывающей линии насосной установки надо иметь в виду, что
давление перед насосом можно
снизить до значения, меньшего давления упруго-
сти паров. В таком случае возникает кавитация и необходимо предложить ме-
ры, предотвращающие это явление (увеличение диаметра всасывающей ли-
нии насосной установки, подключение лупинга и т.д.), и провести повторный
расчет установки.
При выполнении задания требуется обратить внимание на указания в
примечаниях, в которых
даны условия, зависимости и значения, необходимые
для выполнения курсовой работы.
Недостающие величины (физические свойства жидкостей, шероховатость
трубопровода, характеристика насоса и т .д.) могут быть взяты из любых спра-

Глава 6. Рекомендации по выполнению курсовой работы 59
вочных пособий по гидравлическим расчетам. Некоторые справочные вели-
чины приведены в Приложении к данному учебному пособию.
Пояснительная записка к курсовой работе формируется в следующей по-
следовательности:
1. Титульный лист.
2. Задание на курсовую работу.
3. Введение, в котором излагаются аспекты прикладного применения зада-
чи, ее использования на практике.
4. Постановка задачи, где
приводится схема гидравлической системы, ис-
ходные данные, расчетные и геометрические параметры, физические свойства
жидкости, подробно формулируется задание.
5. Содержательная (расчетная) часть пояснительной запаски включает в се-
бя ряд разделов, соответствующих отдельным пунктам задания.
В каждом разделе необходимо вначале привести теоретическое обоснование
решаемой задачи, далее сделать соответствующие расчеты и привести результаты
расчетов в виде таблиц, графиков, программы для вычисления на ЭВМ.
6. Выводы, где должен быть сделан анализ полученных результатов и вне-
сены предложения по улучшению работы установки.
Ниже приводится примерный вид содержания пояснительной записки для
одного из вариантов.
Введение (не нумеруется).
1. Постановка задачи.
2. Определение минимального диаметра всасывающего трубопровода
.
2.1. Сущность кавитационных явлений.
2.2. Расчет минимального диаметра из условия отсутствия кавитации.
3. Определение рабочей точки насосной установки.
3.1. Основные сведения о насосах и построение характеристики насоса.
3.2. Построение характеристики сети.
3.3. Определение координат рабочей точки и мощности на валу насоса.
4. Регулирование подачи насоса.
4.1. Определение числа оборотов вала насоса при измененной
подаче.
4.2. Определение диаметра лупинга.
5. Определение времени опорожнения резервуара.
Выводы (не нумеруются).
Пояснительная записка должна быть выполнена в соответствии с ГОСТом
и иметь определенный порядок вложения и оформления листов:
- на титульном листе рамка соответствующего размера и содержания;
- стандартный лист “Пояснительная записка”;
- стандартный лист “Задание на курсовую работу”;
- “Содержание” пояснительной записки с большим штампом в нижнем правом
углу;
- упрощенный штамп в нижнем правом углу каждого последующего листа с
номером страницы;

60
Гидромеханические расчеты трубопроводных систем
с насосной подачей жидкости
- все рисунки и графики должны иметь заглавие (вверху) и сквозной порядко-
вый номер (внизу);
- при проведении расчетов на калькуляторе графики должны выполняться на
миллиметровке.
Курсовую работу студент защищает перед комиссией, которая и выставля-
ет оценку.
Библиографический список
1. Рабинович Е.З., Евгеньев А.Е. Гидравлика.- M.: Недра, 1987.-234с.
2. Мирзаджанзаде А.Х., Ентов В.М. Гидродинамика в бурении.- М.: Недра, 1986. -
196с.
3. Раинкина Л.Н., Санина Г.И. Определение коэффициента гидравлического тре-
ния,- Ухта: УИИ, 1995,- 25с.
4. Раинкина Л.Н. Гидромеханические расчеты в бурении.- Ухта: УИИ, 1993.- 95с.
5. Башта Т.
М. и др. Гидравлика, гидромашины и гидроприводы,- M.: Машино-
строение, 1982.- 422с.
