Раинкина Л.Н. Гидромеханические расчеты трубопроводных систем с насосной подачей жидкости

Подождите немного. Документ загружается.

Глава 3. Расчет всасывающей линии насосной установки 41

Глава 3

Расчет всасывающей ли-

нии насосной установки

В большинстве практических случаев жидкость поступает в насос из резер-

вуара, расположенного ниже оси установки насоса.

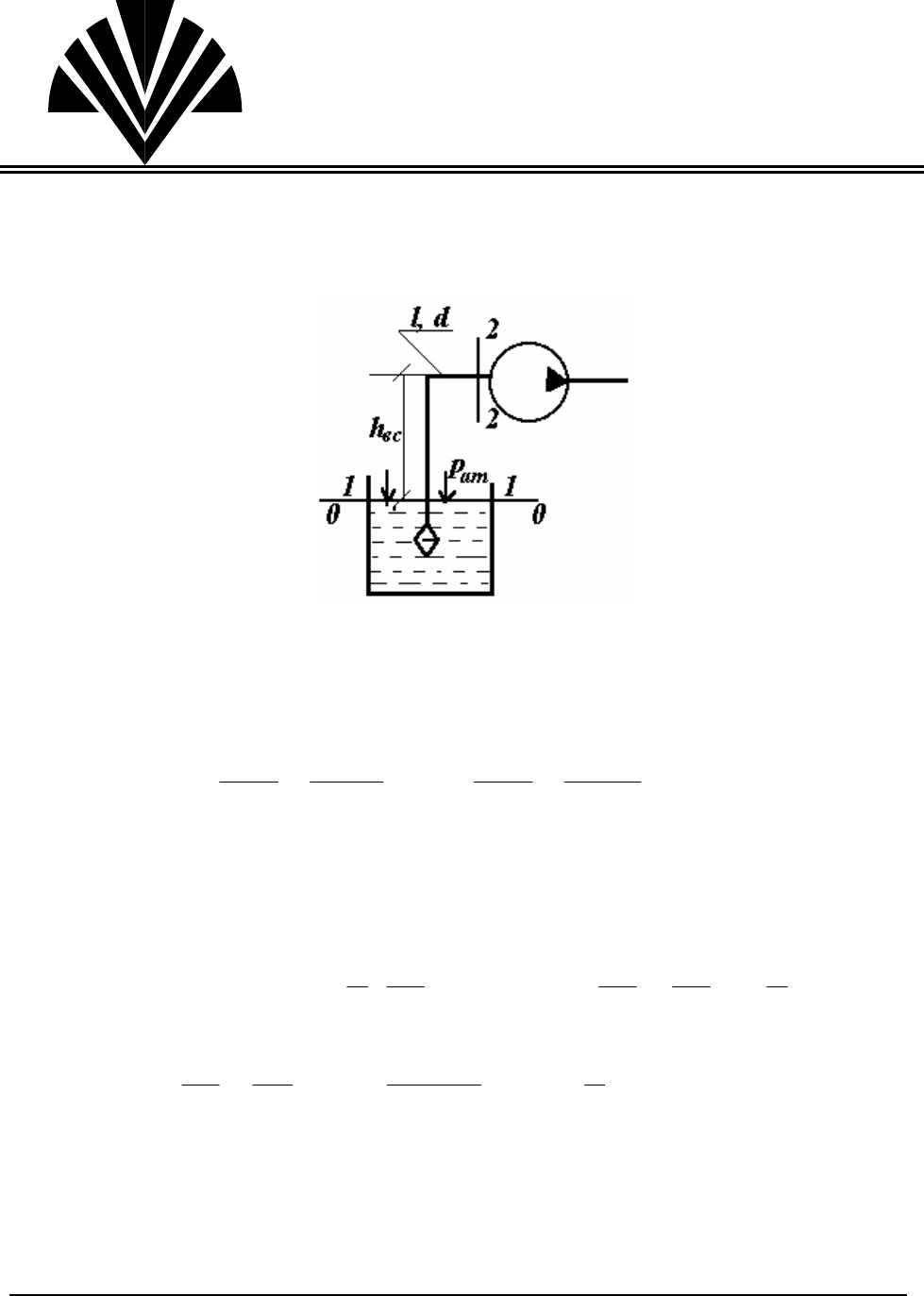
К расчету всасывающей линии

Рис.24

Запишем уравнение Бернулли для сечений

1-1 и 2-2 относительно плоско-

сти сравнения

0-0, преобразуем его в соответствии с данной задачей и определим

давление на входе в насос:

111

222

⋅

+=+

⋅

−

αϑ

(49)

=0; p

ат

;

≈

=Q/

тр

; z

вс

;

тр

/4;

hh h

dg g g

дл м ф12

222

−

=+ =⋅⋅+ + =⋅ +

∑∑

ξξ

ϑϑ

λξ

222

() ( )

пов

ρρ ω

αλ ξ

=−−

⋅

∑

ат

вс

тр

()

(

50)

Анализ уравнения (50) показывает, что абсолютное давление на входе в на-

сос меньше атмосферного, и при некоторых значениях параметров

Q, h

вс

и d его

величина может стать равной нулю и даже принимает отрицательное значение.

Возможны ли такие ситуации в реальной жизни? Нет!

Гидромеханические расчеты трубопроводных систем

с насосной подачей жидкости

Минимально возможное давление в жидкости равно давлению насыщенного

пара, то есть тому давлению, при котором жидкость начинает кипеть. Давление

насыщенного пара зависит от рода жидкости и температуры (Рис.25, Приложение

3).

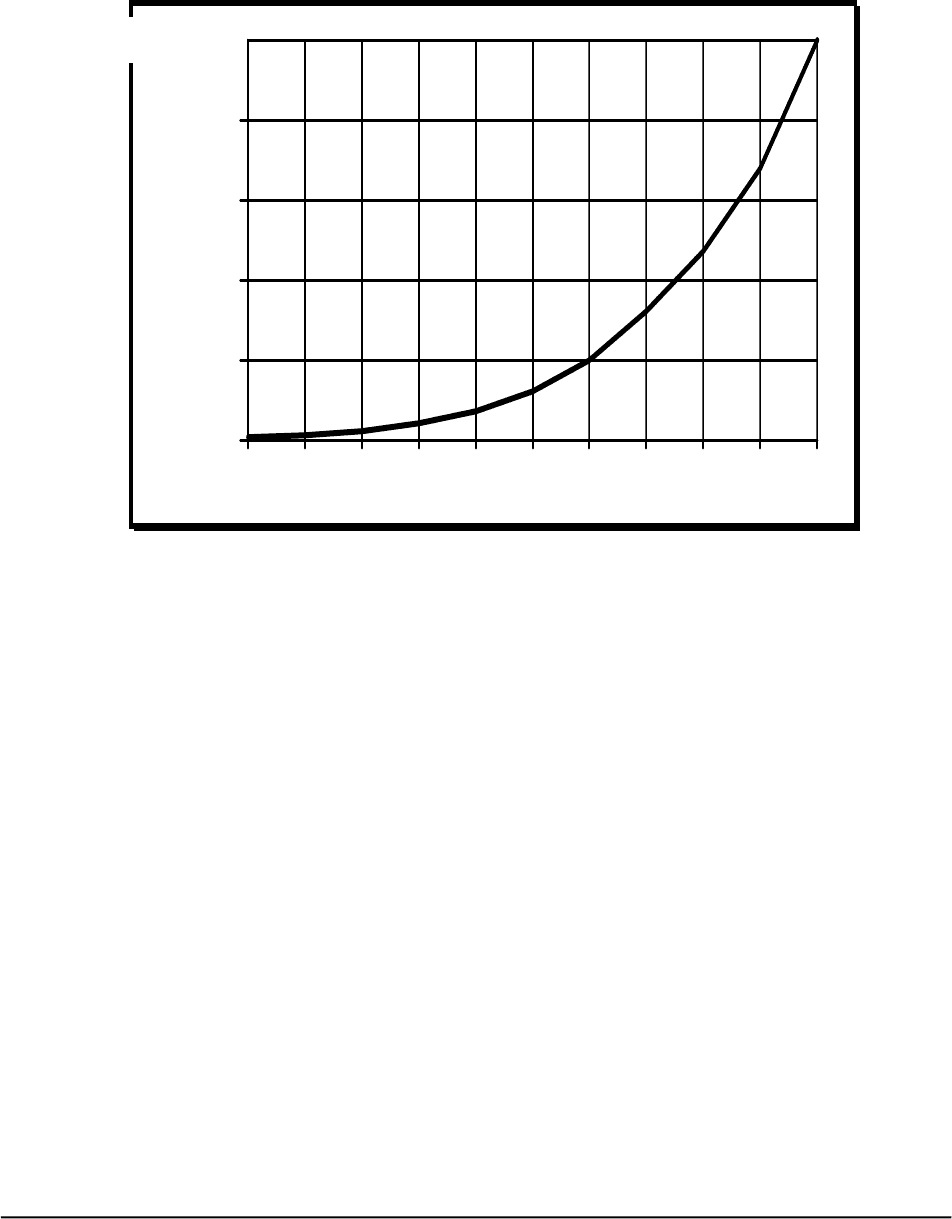
Зависимость давления насыщенного пара воды от температуры

20000

40000

60000

80000

100000

0 102030405060708090100

Рис.25.

Явление кипения жидкости при давлениях меньших атмосферного и

нормальных температурах (10

°, 20°,30°,.....), сопровождающееся схлопыванием

пузырьков пара в областях повышенного давления, называется кавитацией.

Пузырьки пара, выделяющиеся при кавитации, разрывают межмолекуляр-

ные связи, поток жидкости при этом теряет сплошность, столб жидкости во вса-

сывающем трубопроводе отрывается от насоса и процесс всасывания прекращает-

ся. Кроме того, пузырьки пара, попадая вместе с жидкостью внутрь насоса, где

давление больше давления насыщенного пара, лопаются. При схлопывании пу-

зырька на твердой поверхности жидкость, устремившаяся в освободившееся про-

странство, останавливается. При этом ее кинетическая энергия превращается в

потенциальную и происходят местные гидравлические удары. Это явление сопро-

вождается существенным ростом давления и температуры и приводит к разруше-

нию материала поверхности.

инженерной практике существует правило: Не допускать кавитации!

Для этого необходимо, чтобы в сечениях потока, где давление меньше ат-

мосферного, было выдержано условие:

Давление в жидкости больше давления насыщенного пара (

р > p

н.п

). Это

условие отсутствия кавитации.

н.п

, Па

t,°C

Глава 3. Расчет всасывающей линии насосной установки 43

Кавитационные расчеты всасывающей линии насосной установки заключа-

ются в следующем:

1. Проверка условия

> p

н.п.

- давление на входе в насос р

определяется из

уравнения (50) при известных параметрах

Q, d, h

вс

2. Определение предельных значений параметров

Q, d, h

вс

из уравнения

(50) при

= p

н.п..

3.1. Определение минимального диаметра трубопровода

Для примера расчета, рассмотренного в разделе 1.4., определим минималь-

ный диаметр всасывающего трубопровода из условия отсутствия кавитации.

Дано:

Подача насоса Q=90

⋅10

-3

/с ; длина трубопровода l=35м; высота всасыва-

ния = 3 м; коэффициент сопротивления фильтра

= 5,2; коэффициент сопротив-

ления поворота

пов

= 1,32; давление насыщенного пара воды при температуре

°С - р

н.п.

= 7350 Па; абсолютная шероховатость поверхности трубопровода

0,5 мм; атмосферное давление равно 10

Па.

Последовательность решения задачи

1. Преобразуем уравнение Бернулли (50) следующим образом: в

левой час-

ти сгруппируем слагаемые,

не зависящие от диаметра, а в правой части - зави-

сящие от диаметра

ат

вс

−

−=

⋅

⋅⋅

∑

αλ ξ

()

(

51)

Задача заключается в определении диаметра из уравнения (51). Поскольку

при разных значениях диаметра может быть различный режим движения в трубо-

проводе (

Re=

ϑ⋅

⋅ρ

), и коэффициент гидравлического трения

зависит от диа-

метра сложным образом:

=64/Re при ламинарном режиме и

=0,11

⋅

(68/Re+

)

0,25

при турбулентном режиме, уравнение (51) в общем случае является транс-

цендентным. Трансцендентным называется уравнение, которое не решается ал-

гебраическими методами. Такие уравнения решаются графическим способом или

численными методами с помощью ЭВМ.

2. Графический метод решения уравнения (51).

Этот метод уже был изложен ранее при определении параметров лупинга (пара-

граф 2.1.2.).

Обозначим:

8⋅

⋅⋅

++ =

∑

αλ ξ

()()

Задается несколькими значениями диаметра d, вычисляем значение функ-

ции

f (d) и строим график этой функции. Далее откладываем на оси ординат вы-

численное значение левой части уравнения (51) и находим при этом значении

функции расчетное значение диаметра. Иными словами, решение уравнения есть

Гидромеханические расчеты трубопроводных систем

с насосной подачей жидкости

точка пересечения двух функций диаметра - левой и правой частей уравнения

(51).

Вычисления выполнены с помощью

Microsoft Excel.

диаметр,

мм

40 80 120 160 200 240

число Re

4,37E+06 2,19E+06 1,46E+06 1,09E+06 8,75E+05 7,29E+05

3,68E-02 3,10E-02 2,80E-02 2,61E-02 2,48E-02 2,38E-02

(d)

123,13 24,32 7,70 3,15 1,52

левая часть 6,53 6,53 6,53 6,53 6,53 6,53

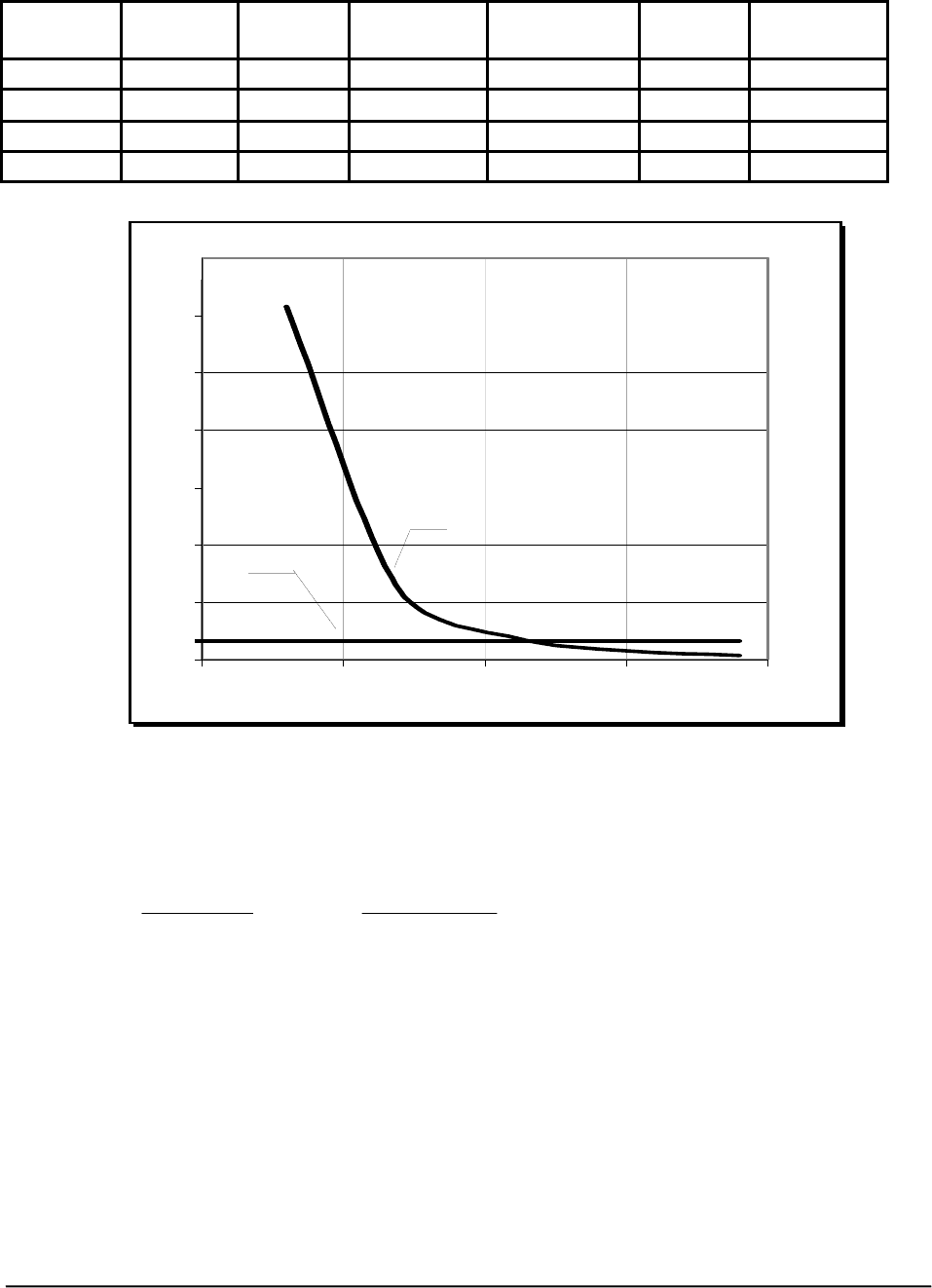
Определение минимального диаметра всасывающего трубопровода

100

120

140

50 100 150 200 250

d,мм

1- график правой части уравнения (51), 2- график левой части уравнения

(51).

Рис.26.

Левая часть уравнения (51) равна:

ат

вс

−

−=

−

⋅

−= −=

10 7350

992 9 8

39533653

На пересечении графика функции f(d) с расчетным значением этой функции

числом 6,53 получаем точку, абсцисса которой равна 165 мм. Это и есть ис-

комое минимальное значение диаметра трубопровода из условия отсутствия кави-

тации:

min

= 165 мм.

3.2. Определение максимального расхода жидкости

во всасывающем трубопроводе

Определим максимально возможный расход жидкости во всасывающем трубо-

проводе заданного диаметра

d = 200 мм (пример 1.4) из условия отсутствия кави-

тации. Для этого в уравнении Бернулли (51) обозначим:

Глава 3. Расчет всасывающей линии насосной установки 45

8⋅

⋅⋅

++ =

∑

αλ ξ

()()

(

52)

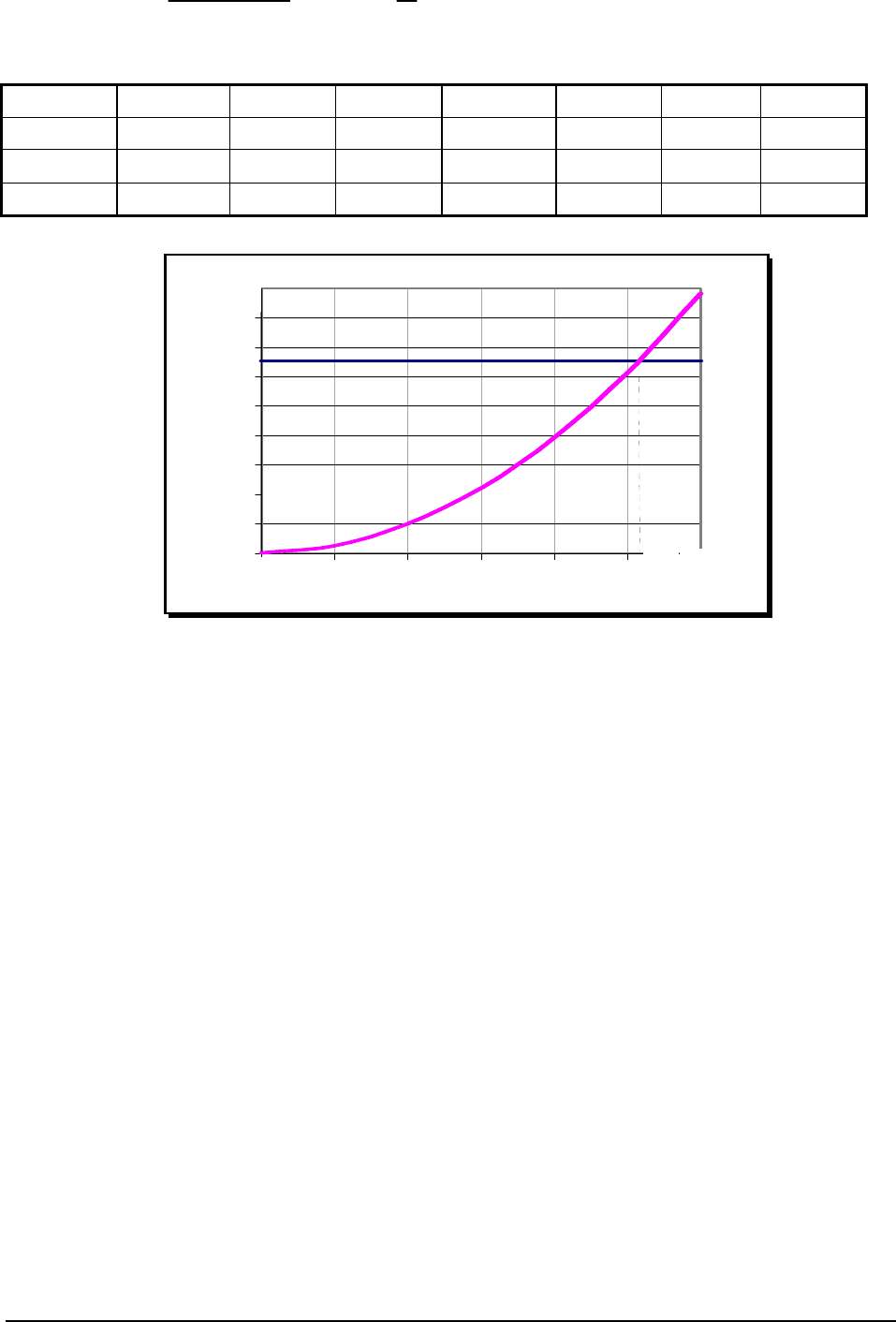
Уравнение (52) решено графическим способом с помощью Microsoft Excel.

расход Q

0,00001 20 40 60 80 100 120

число Re

1,08E-01 2,16E+05 4,32E+05 6,48E+05 8,64E+05 1,08E+06 1,30E+06

5,51E-01 2,53E-02 2,50E-02 2,49E-02 2,48E-02 2,48E-02 2,47E-02

(Q)

0,00 0,25 0,98 2,21 3,93 6,13 8,83

Определение максимального расхода во всасывающем трубопроводе

1E-05 20 40 60 80 100 120

(Q)

Q,л/с

Рис.27.

Из Рис.27 следует, что

max

=104 л/с.

3.3. Определение максимального коэффициента сопротивления

фильтра или максимально возможной высоты всасывания

Анализируя уравнение (51), замечаем, что при заданных значениях пара-

метров

Q и d давление на входе в насос может стать меньше давления насыщен-

ного пара при условии, если:

1. Высота всасывания

вс

превысит допускаемую ;

2. Засорится фильтр 4 и коэффициент сопротивления фильтра превысит

свое предельно возможное значение.

Расчет предельных значений

вс

или

производится непосредственно по

уравнению (51) при

=р

н.п.

и не вызывает затруднений.

Гидромеханические расчеты трубопроводных систем

с насосной подачей жидкости

Глава 4

Расчеты на прочность

элементов

гидравлической сети

Гидравлическая сеть представляет собой систему трубопроводов и резер-

вуаров, соединенных между собой определенным образом. Стенки трубопрово-

дов, равно как и стенки закрытых резервуаров, могут находиться под действием

высоких избыточных давлений. При этом возникают большие разрывающие уси-

лия, которые могут превысить предельно допускаемые для данной конструкции

из условий прочности.

Для предотвращения

аварийных ситуаций необходимо прогнозировать

максимально возможные давления в системе и определять предельные значения

конструктивных элементов гидравлической сети. В данном разделе показано, как

это делается.

4.1. Определение минимальной толщины стенки

из условия прочности при гидравлическом ударе

На практике в трубопроводе возможно резкое повышение давления (гид-

равлический удар) вследствие внезапного торможения движущейся в нем жидко-

сти. Это явление возникает, например, при быстром закрытии различных запор-

ных устройств, устанавливаемых на трубопроводах (задвижка, кран), клапанов,

внезапной остановке насосов, перекачивающих жидкость и др. Гидравлический

удар может привести к повреждениям мест

соединения отдельных труб (стыки,

фланцы), разрыву стенок трубопровода, поломке насосов.

Повышение давления при гидравлическом ударе определяется по формуле

Н. Е. Жуковского :

р =

ρ⋅

⋅ϑ

(53)

где:

- плотность жидкости,

- скорость движения жидкости в трубопроводе

до удара,

с - скорость распространения волны гидравлического удара.

⋅+

⋅

()1

тр

(54)

где:

- модуль упругости жидкости (справочная величина, Приложение

6),

тр

- модуль упругости материала стенок трубопровода (Приложение 7), d-

внутренний диаметр трубопровода,

- толщина стенки трубопровода.

Глава 4. Расчеты на прочность элементов гидравлической сети 47

При резком закрытии крана 5 на напорном трубопроводе (Рис.13) происхо-

дит гидравлический удар, и давление

р перед краном становится равным:

р = р

(55)

где

- давление на выходе из насоса в момент удара,

р - повышение давления

при гидравлическом ударе.

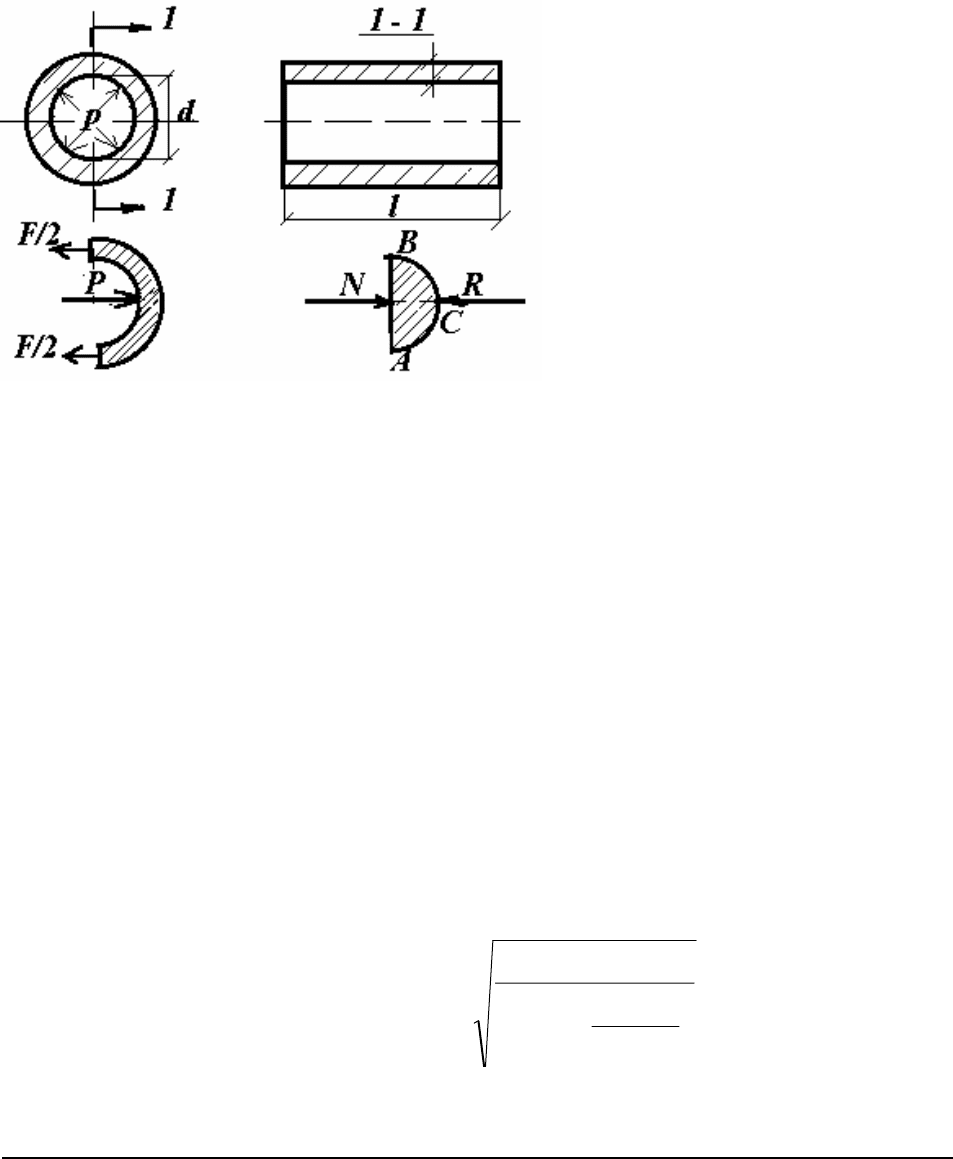
Определим разрывную силу

P, которая будет действовать на стенки трубо-

провода при гидравлическом ударе. Для этого рассмотрим равновесие жидкости в

объеме полуцилиндра

ABC (Рис.28).

Иллюстрация к расчету толщины стенки трубопровода

Условие равновесия жидкости в

объеме полуцилиндра

ABC:

R = N,

где R - реакция полуцилиндриче-

ской поверхности ABC. Она рав-

на по величине и противополож-

на по направлению искомой раз-

рывающей силе

N -

реакция сжатой жидкости,

находящейся слева от

поверхности

AB.

Рис.28.

Сила

N равна силе давления жидкости на поверхность прямоугольника с размера-

ми

d, l.

Учитывая, что N=p

⋅

l , получим:

R =N= P = p

⋅

(56)

Разрывающая сила

P вызывает появление силы сопротивления F в мате-

риале стенки трубопровода и внутренних растягивающих напряжений, связанных

с силой

F следующим уравнением:

F =

σ⋅

⋅

(57)

В момент разрыва

= [

] - допускаемому напряжению на разрыв, а толщи-

на стенки

при этом минимальна,

min

Приравнивая в этой ситуации силы

P и F, получим:

⋅

l = [

]

⋅

min

⋅

l ,

откуда:

min

= p

⋅

d / 2[

]

(58)

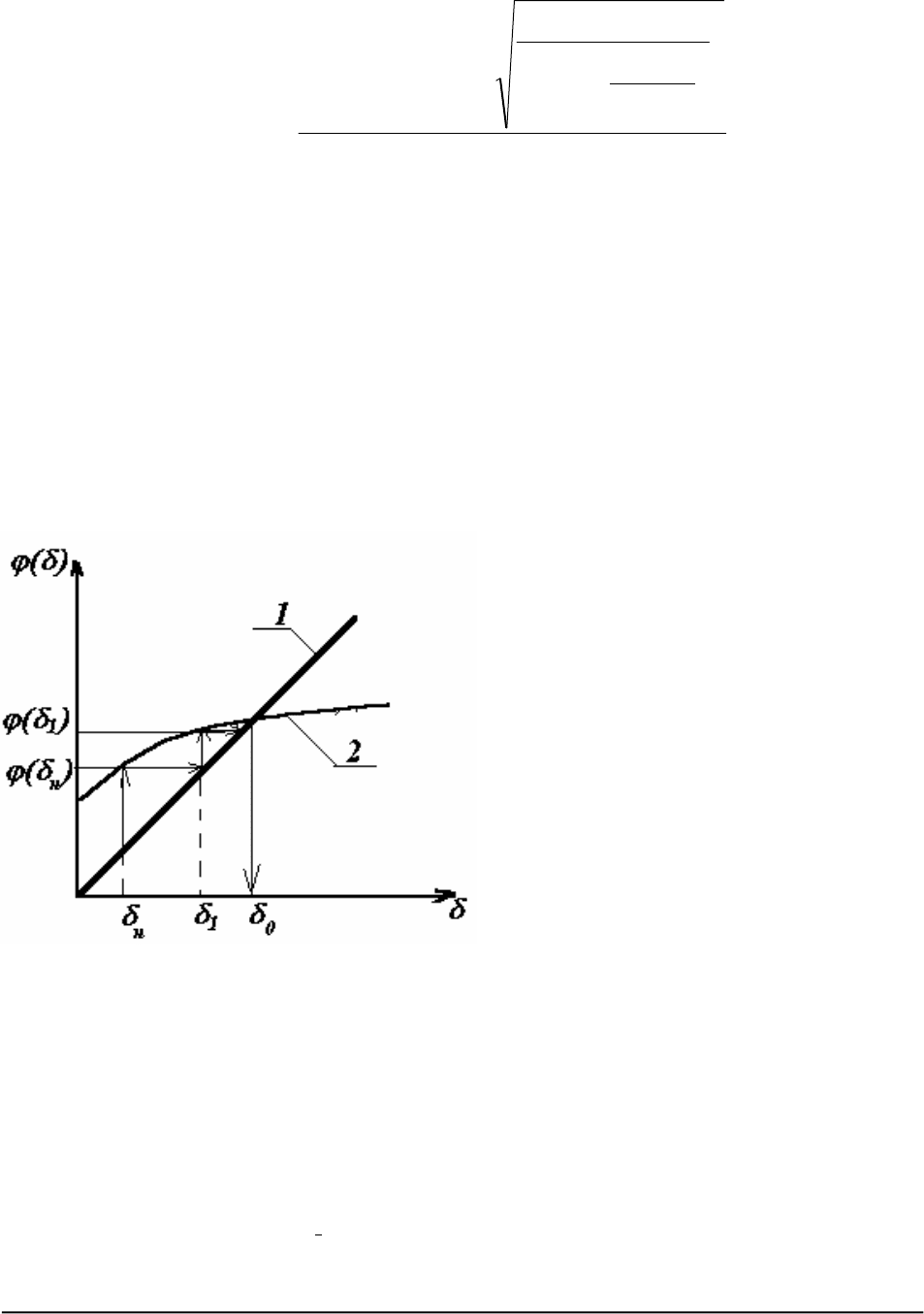
Из зависимостей (53), (54) и (55) имеем:

=+⋅⋅

⋅+

⋅

тр

ρϑ

()1

(59)

Гидромеханические расчеты трубопроводных систем

с насосной подачей жидкости

Подставляя (59) в (58), получим уравнение для определения

min

[]

ρϑ

min

тр

⋅+⋅⋅

⋅+

⋅

(

()

)

(60)

Зависимость (60) есть трансцендентное уравнение относительно

min

Это уравнение можно решить графическим способом или с помощью ЭВМ одним

из известных численных методов (итераций, половинного деления и др).

Графический способ подробно изложен в Разделе 3. Здесь покажем, как ре-

шается трансцендентное уравнение на ЭВМ методом

итераций.

Для использования этого метода

необходимо представить исходное

уравнение в виде: параметр равен функции от параметра

. Уравнение (60) уже

имеет такой вид:

= f (

Графическое изображение левой и правой частей уравнения (60) показано

на Рис.29.

Иллюстрация метода итераций

1.Задаемся любым значением пара-

метра

, например,

2. Определяем при этом значении па-

раметра значение функции

(

3. Присваиваем значение функции

значению параметра

4. Находим при

значение

(

) и

так далее до тех пор, пока последую-

щее и предыдущее значение функции

не совпадут с заданной точностью.

- изображение левой части уравнения (60)-

; 2 - изображение правой части

уравнения (60)-

пр

(

);

- решение уравнения (60).

Рис.29.

Последовательность численного решения уравнения (60)

методом итераций.

1. Приводим уравнение (60) к безразмерному виду. Для этого вводим

безразмерную переменную

безр.

/d и вместо (60) получим:

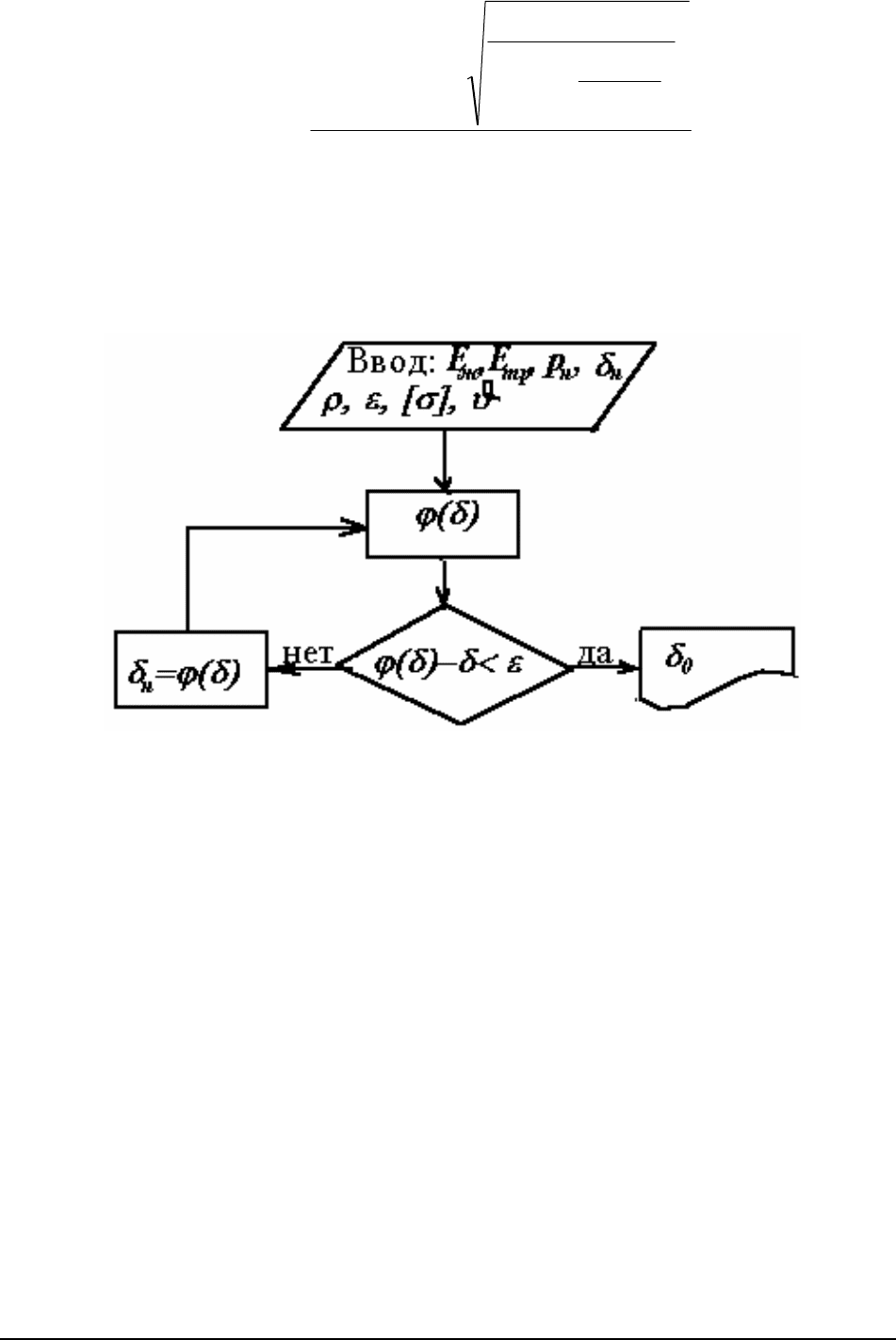
Глава 4. Расчеты на прочность элементов гидравлической сети 49

[]

ρϑ

безр

тр

+⋅⋅

⋅+

⋅

(

()

61)

2. Составляем блок-схему вычисления величины

0 безр

(в дальнейшем ин-

декс “безр.” опущен).

Блок-схема вычисления параметра

0 безр

методом итераций

Рис.30.

4.2. Определение минимальной толщины стенки

закрытого резервуара, находящегося

под внутренним избыточным давлением жидкости

При автомобильном или железнодорожном транспорте нефти или нефте-

продуктов жидкость обычно нагнетается с помощью насоса в закрытые сфериче-

ские или цилиндрические емкости, затем их погружают на

транспортные средства.

По соображениям экономии средств на перевозку желательно поместить в

сосуд определенного геометрического объема максимально возможное количест-

во жидкости, при этом создается

высокое избыточное давление в резервуаре и, ес-

ли стенки его недостаточной толщины или сварные швы выполнены без нужного

запаса прочности, может произойти авария.

Аналогичные задачи возникают при расчете на прочность резервуаров для

сбора нефти на нефтяных промыслах.

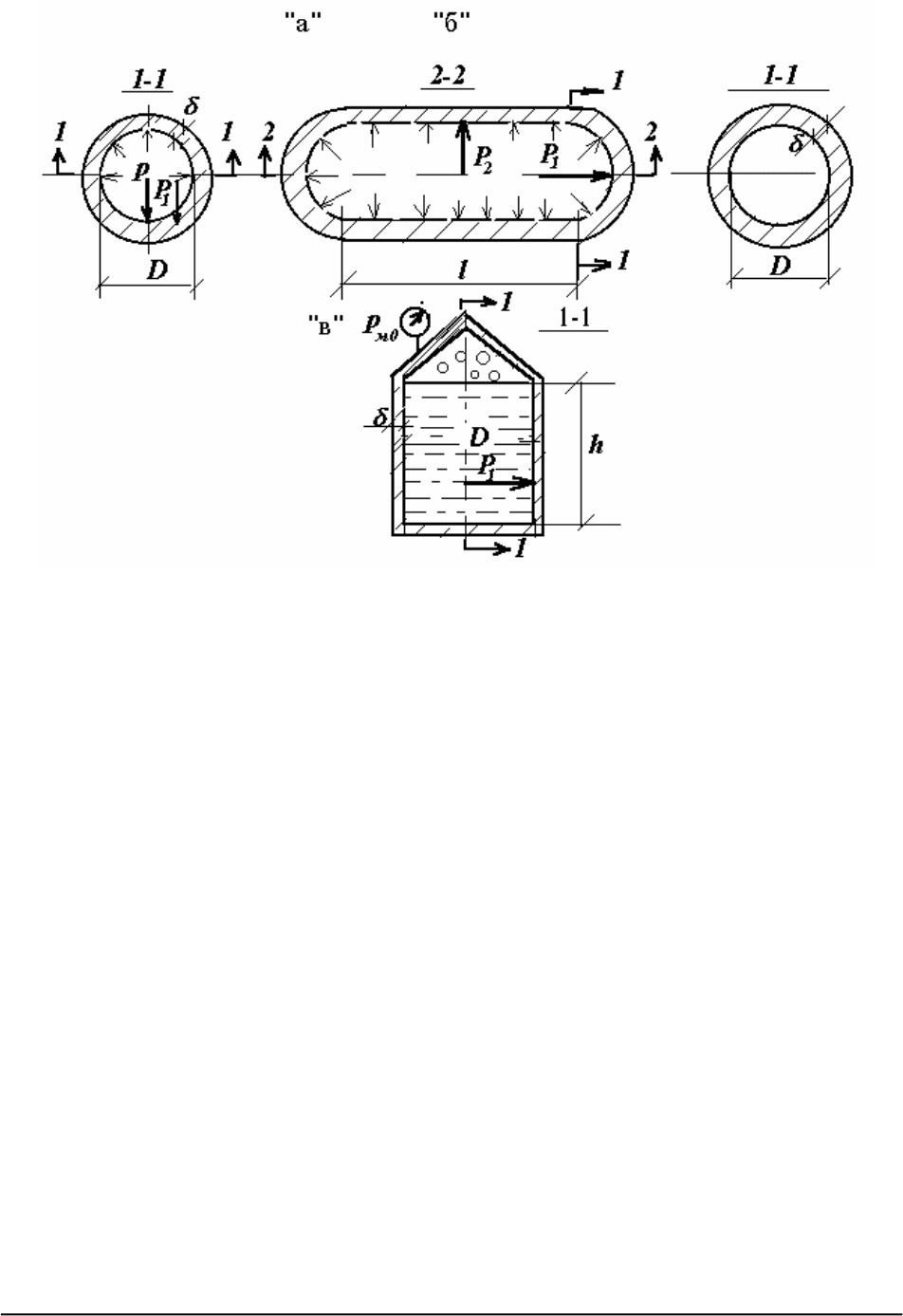
Получим расчетные зависимости для резервуаров, изображенных на Рис.31.

Иллюстрация к определению толщины стенки

резервуара

Гидромеханические расчеты трубопроводных систем

с насосной подачей жидкости

"a" - сферический резервуар ; "б" - цилиндрический резервуар со сфериче-

скими боковыми крышками; "в" - вертикальный цилиндрический резервуар для

хранения нефти: дно - плоское, крыша - коническая,

м0

- избыточное давление

паров над уровнем жидкости.

Рис.31.

Для получения расчетных зависимостей необходимо приравнять разры-

вающую силу силе сопротивления, возникающей в материале стенок. В свою оче-

редь разрывающая сила определяется из условия равновесия соответствующего

объема жидкости (Рис.32).