Пытьев Ю.П., Шишмарев И.А. и др. Задачи по теории вероятностей и математической статистике

Подождите немного. Документ загружается.

I у мощность потока

излучения.

I !.'). Обозначим

через

("t^) —О и

(M(i) = 0)

события,

|Ц*|>м"|И1'

в излучении

и неизлучении частицы радиоактивным

Мнмпм \п

время

Ь .

Используя независимость

вероятности не-

||«у ПИ

от

расположения промежутка

на оси времени и

не-

ННВМЯность производной

4хР

(тЦ

)=0) , доказать,

что

p(m(i)=

В** 1Й.Ч.

Пусть

в условиях задачи

12.3

- период

IMVI"

шада.

Полное количество излученных

частиц (однород-

на радиоактивным веществом) к

моменту временив равно

М({)~

L | '"«(О.

где сумма берется по

М. радиоактивным атомам в

•I'i'mminh

момент времени

4*0 .

Пусть

~K(Ej)- вероятность

1М»чп||ИЯ частицы с энергией

Е^.

€ & ,

WJ i .

Предположив,

что события, связанные

с излуче-

ш«м атомов, независимы,

получить распределение

вероятностей,

Ми<ипппцпс

векторный поток излучения

частицМ(£)= ...,№„(!!))

1пп«ный потокM(i)*Mitt)t""+M*(4) , где

Mj(i) -

поток

Мтии

энергией

Ej .

| II."э.

Пусть векторный поток излучения

р1(i)

= (M

(l),...

LMJi))

описывается

распределением вероятностей:

и.

о#»)«м., Oi^jr^M., а

Ншннпть,

что парциальные потоки

ЩИАКтнм распределением вероятностей

«.г), С^

(CLjU-<;"f

(i- a.;(t-*

)) 0#ГчМо

• чк>

инбые пары парциальных потоков

М{(4), Mj

(i),

L*},

1|1в1, , И

задастся

распределением вероятностей

U^rjS: л

е>

"Vit'jf * По,

M.!

п '

' =

L/M„ " Z/KM.-fc-rj-)!

12.6.

Рассчитать

характеристическую

функцию

пуассонов<

ского распределения векторного потока излучения

N(t)

по:

ного потока

NW) (задача 12.2), характеристическую функ-

цию распределения векторного потока

М радиоактивного

распада и полного потока

М(4)

с тем

*е распределением по

спектру энергий, что и

NCf)

(задача

12.4) .

Показать,

имеет место сходимость по

распределению: ,

M&^/Vft)

при

*1-+О

так, что

М."* = ty = Cons* -

мощность

излучения.

12.7.

Для пуассоновского векторного потока

излучения

W£0= (NiCf),Wn. (i)) с

распределением по спектру

энерги!

мощностью ty

найти

среднее

Nj (i)

» дисперсию Й

Nj (i)

мощности усредненных

пар

циальных излучений

12.8.

Для векторного потока излучения

радиоактивного

распадаM{i)=(Mj&),..., M^d))

(задача

12.4 )

найти

среднее

, дисперсию Ъ Mj[i)

CX)v(M

(

(h)Mjt

= 1

>->

12.9.

Пусть на миаень падает векторный поток

частиц

Nn li))

с заданным

распределением вероятное

Мишень пропускает частицы с энергией Е^е

g> с вероятностью

Р/

•••» ^ •

Найти распределение

вероятностей

векторного потока излучения, прошедшего через михень.

Найти

распределение вероятностей суммарного потока излучения,

про

шедшего через мишень

случае пуассоновской модели

и в слу-

чае модели радиоактивного распада

(см. задачи 12.2 и

12.4 ) .

12.10.

Пусть

задаче

12.9 частицы

за мипенью

регист-

рируются детектором

в определенном

телесном угле

2 . Пред-

полагая,

что источник излучения изотропный и что

частицы

фаашфувтоя детектором

вероятностью

00 ,

найти

вероятность

что детектор за время

~Ь зарегистрирует Ъ частиц.

12.II.

Измерение излучения осуществляется до

накопления

имреиг «енного суммарного количества частиц

N(t")

= t . Пока-

••ft.,

что вклады парциальных потоков

случае

пуассоновской

ИМ»ли

излучения

модели излучения радиоактивного раопада

нр<1двлением

по

спектру энергий

GLj =К ^

р®/*

описываются

распределением вероятностей

У,'.12.

Для пуассоновского процесса

P{Nft)=kj=

~ Kl ^ , К«ОД,_ ,

начинающегося

нуле

P{A/(0)=0j =

щучпиный момент

достижения целой положительной

величи-

ну

определяется из

Р = Р{ * М} .Найти

мютнооть распределения

Т*м и

среднее значение

7м .

12.13.

Рассмотрим два независимых пуассоновских

процес-

са,

начинающихся

в нуле:

Ияйти распределение вероятностей случайной величины,^

A/^fe),

|Ц 7'м -

случайный момент, определяемый

из

12.14.

Найти математическое ожидание

и дисперсию случай-

ной величины ,

рассмотренной

предыдущей

задаче.

I/.I5.

Пусть

сумма

К.

независимых случайных

вели-

чин

^ ,

одинаково распределенных

по

закону,

полученному в

МДаче 12.13.

Найти распределение

^h. и относительную точ-

иооть: МК-

12.16. Показать,

что

из

среднеквадратичной непрерывнос-

ти

процесса

точке

вы-

l-*io

отохастическая непрерывность процесса

точке

т... lim P{|£ft)-^)/>e}=o, £>о.

-»te

12.17. Показать,

что пуассоновский процесс

и процесс

радиоактивного

распада стохастически непрерывны в точках

12.18. Гильбертов случайный процесс

-оо дифференцируем в среднеквадратичном в то

ке "to ,

если

существует

А-*о

-п.

Случайная величина называется среднеквадратичной

про

изводной случайного процесса

^ (О в

точке

Ьо . Показать

что М ^ tt)

^ £ & и производная

справа

существуе

12.19. Доказать,

что

нормального стационарного

марко:

ского процесса корреляционная функция равна

с1>0

(теорема

Дуба) .

12.20.

Найти распределение случайной

величины:

где ^(f) -

координата броуновской частицы,

при t= О

находившейся

начале

координат.

12.21.

Найти распределение

случайной величины S (О ,

где ^ -

момент достижения броуновской

частицы максимальной

координаты в

интервале

£) : % (S)

§13. Распределение

ортогональных проекций.

Понятие

задаче статистической проверки

гипотез

13.1. С 187I

по

1900

гг.

Швейцарии родилось

I 359 67

мальчиков

и I 285 086

девочек. Используя

критерий 36" провв'

рить две

гипотезы:

первая

вероятность рождения

мальчика

равна

0.515,

вторая

вероятность рождения мальчика

равна

0.5.

13.2.

Стальная проволока выдерживает

в среднем растяги-

вающее усилие

«6720 кг/см^. Стандартное уклонение*

£Г от-

дельных

образцов от этого среднего равно

220 кг/см^. Извест-

но,

что

в отношении растягивающих

усилий

9С£ , выдерживаемых

отдельными

образцами

проволоки,

имеет место

нормальный закон

распределения. Результаты

испытаний двух партий

проволоки

Стандартное уклонение

то

же,

что

среднеквадратичное ук-

лонение.

Термин употребляется

в математической статистике.

•••тин

таблице: ^

1-я

партия

(Ocf) 2-я

партия

(ОС* )

г,300 6900 7150 7280

6670 7130 6950 7120

d720 6690 7230 6690

6900 6750 7240 7070

6780 6560 7090 6950

6780 6700 6800 6590

6780 6930 7000 6890

6720 6720 7070 6910

6630 6950 6700 6630

6660 6960 7140 7220

^|||М»вно

ли

на

основании этих испытаний утверждать, что

обе

[•Аргии

проволоки требуемого качества

результаты испытаний

^Ндуят

объяснить

случайностью выборки?

Воспользоваться

кри-

fариям % .

13.3. Известно,

что

определенный

сплав не

поддается

|йр|>ояии

среднем

течение

875

дней

со

стандартным ^.оне-

иаам,

|in иным

дням.

Указать,

какое количество листов

дан-

опяпва должно быть подвергнуто испытанию,

чтобы с веро-

•ТМШ1Т1.» 0.90

ожидать величину уклонения

от

средней не

боль-

аа,

чем на

5*.

I ).4. Приводимая

ниже таблица дает

среднюю

длину

0С

••Инн пукувки вообще, среднюю

длину

ОС;

яйца кукушки,

поло-

манною

гнездо

определенного

вида птиц

ошибки измерений

иияп оценок стандартных

уклонений.

Измерения

производились

У МЯИ|П

обнаружить разницу

размерах

яиц, опускаемых кукуш-

ка *

гнезда различного вида

птиц.

ИШрЯи»———— — — — ——

Число

измерений!

Средняя

длина! Стандартное

Отктпнные яйца! ! в

мм

! уклонение

(п-о, п.О I С0с

,0С^ ! Cg-

6-Q

Пообце 1572 22.3 0.96

й вид

91 21.9 0.79

вид

115 22.4 0.76

I и вид 58 22.6 0.86

шшштт пшч I

—

|ино»1.1ун

распределение Стьюдента, проверить на уровне

значи-

ИИРТИ d «0.11

гипотезу

о том,

что разница

длине

размеров

|ЙН нукушки

от птиц

L-го

вида носит случайный

характер,1=1,

I 1.

13.5. Чтобы

проверить, оказывает ли влияние на

прочное

бетона особый способ его приготовления, были

взяты 6 выборо

разделены случайным образом

на две

группы

из каждой

выбор;

был

сделан пробный

куб, причем

выборки

из

группы II подверг!

лись особой обработке. После

готовности

кубов определили

их

сопротивление

на

сжатие, получив следующие

результаты опыта

Бетон I 290 311 284

Бетон II 309 316 318

Используя распределение Стьюдента, проверить на уровне

знач|

мости

сС

= 5$

гипотезу

о том,

что бетон обеих групп

одинаков<

прочен.

13.6. Были взяты 16

клубней картофеля

и к

каждому

клуб!

были применены

два метода измерения содержания крахмала.

таблице

даны

численные

результаты -

разности между

проценто»

содержания крахмала, определенного I и II методами.

Разности

! *

Разности

0.2 9 0.1

0.0 10

0.2

0.0 II

0.3

4 0.1

12 0.0

0.2 13 -0.1

0.2

0.1

0.3 15

-0.2

-0.3

0.1

С помощью

критерия Стьюдента проверить гипотезу

о том, что

оба метода не дают

систематического

различия

в определении

процентного содержания

крахмала.

Принять ot = 0.05.

13.7.

Для

того

чтобы

исследовать эффект

использования

специальной

сеялки, десять участков земли

были засеяны при

помощи обыкновенной

сеялки

десять соседних

ними

участков

земли были засеяны

при

помощи специальной

сеялки.

Затем сра-

внивались полученные урожаи

зерна, причем

пару

составляли

два соседних

участка.

№ пары

Специальная

Обыкновенная

Разница

сеялка

урожае

8.0

5.6

2.4

2 8.4

7.4

1.0

8.0

7.3

0.7

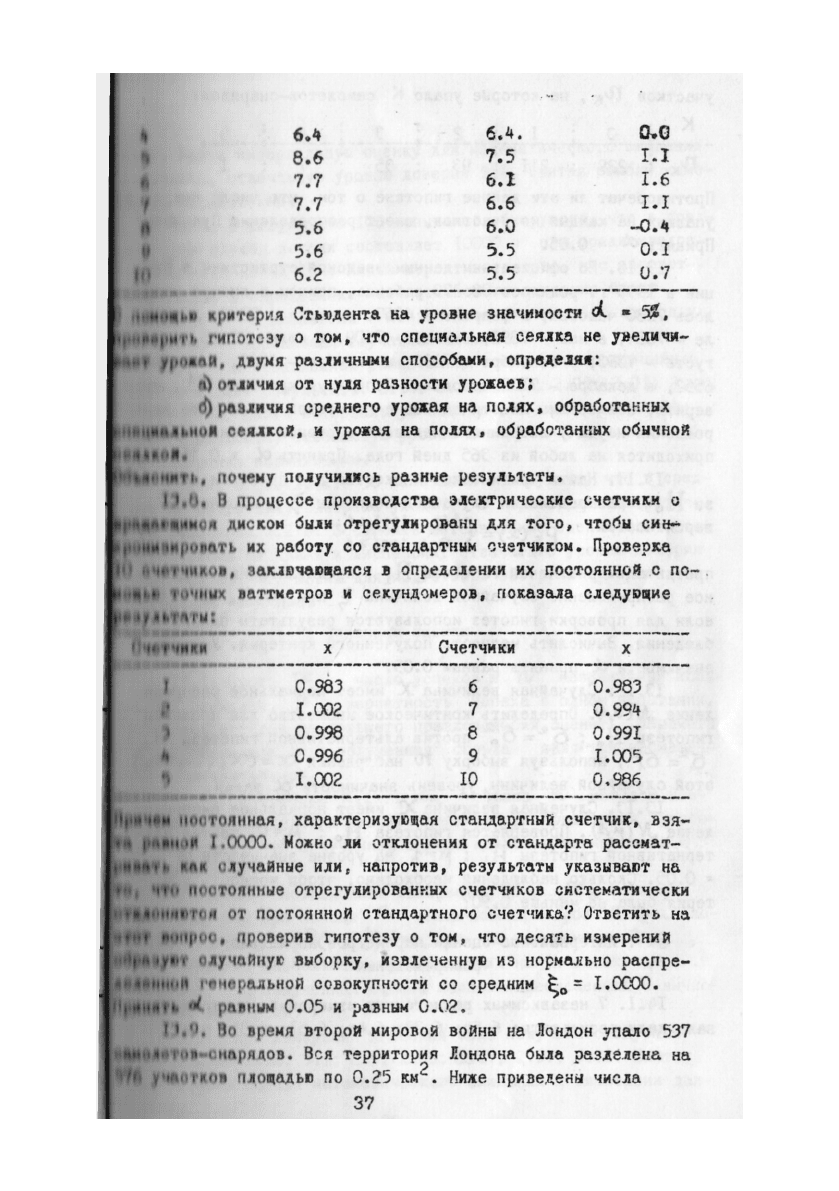
6.4 6.4. Q»G

8.6 7.5 I.I

7.7 6.1 1.6

7.7 6.6 I.I

5.6 6.0 -0.4

5.6 5.5 0.1

6.2 5.5 0.7

^—

критерия Стьюдента на уровне значимости

<к •

•ИТк

гипотезу о том, что специальная сеялка не

увеличи-

уроаай,

двумя различными способами,

определяя:

(О отличия от нуля разности

урожаев;

различия среднего урожая на полях,

обработанных

аьиой сеялкой,

урожая на полях,

обработанных обычной

•«•а.

ии11,

почему получились разные

результаты.

И.м. И

процессе производства электрические счетчики

•ииоя

диском были

отрегулированы

для того, чтобы

син~

яириплть их работу со

стандартным

счетчиком.

Проверка

•Чичиков,

заключающаяся

определении их постоянной с

по-

lb*

точных ваттметров и секундомеров, показала

следующие

lu«Mfttu:

ifHHRM х Счетчики х

I I-.-- —

0.983 6 0.983

1.002 7 0.994

0.998 8 0.991

0.996 9 1.005

1.002 10 0,986

— —

постоянная, характеризующая

стандартный счетчик,

взя-

||1ной I.0000.

Можно ли отклонения от стандарта

рассмат-

•к

кпк случайные

или, напротив, результаты

указывают

на

мочтолнные отрегулированных счетчиков

систематически

ииютом от постоянной стандартного

счетчика?

Ответить

на

ВвЛроо,

проверив гипотезу о

том,

что десять

измерений

IT случайную

выборку,

извлеченную

из нормально

распре-

гпнеральной совокупности со средним

= I.OCOO.

Ifk

рпвным

0.05

и равным

0.02.

11.'J. Во

время второй мировой войны на Лондон упало

537

»епя-'скпряаов.

Вся территория Лондона была разделена

на

уЧАоткпв

площадью

по

0.25 км'.

Ниже

приведены числа

участков

ГС^к

, на

которые упало

К самолетов-снарядов:

К : Q : j :

з ^

*—

—

—±—

—=—4.—

—4.—2—

—

: 229 : 211 : 93 : 35 : 7 : I

Противоречат

ли эти данные гипотезе

том, что

число

снарядо

упавших

на каждый из

участков,

имеет распределение

Пуассона?

Принять

ot = 0.05.

13.10.

По

официальным

данным шведской статистики

в Шве-

ции

в 193'.> г.

родилось

88 273

ребенка,

причем в

январе

роди

лось

728С

человек,

феврале

- 6957, в март

- 7883, в апре

ле

- 7884,

в мае

- 7892,

в июне

- 7609, в

июле

- 7585,

ав

густе

- 7393, в

сентябре

- 7203, в

октябре

- 6903, в ноябре

6552,

в декабре

- 7132 человека. Используя критерий , про

верить, совместимы

ли

эти

данные

гипотезой

о том,

что

день

рождения наудачу выбранного человека

равной

вероятностью

приходится на любой из

365

дней года. Принять

ot 0.1$.

13.11. Найти

критическое множество для проверки

гипоте-

зы

о распределении

случайной величины

^ с плотностью

вероятностей

/-v'\- I*!*-*-,

Р%

Сэ0

-"1 О, |%|>1

против

альтернативной гипотезы Н^ . предполагаюсь нормаль-

ное

распределение

случайной

величины ^ при О, б

если для проверки гипотез используются

результаты

одного

на-

блюдения.

Вычислить мощность полученного критерия.

Уровень

значимости

принять

равным 0.05.

13.12.

Случайная величина

имеет нормальное

распреде-

ление

jyTfOjd).

Определить критическое множество для

проверки

гипотезы Не 6^=6о

против

альтернативной гипотезы H

используя выборку

И/

наблюдений

ОС=

("Х±

"Х^)

этой случайной величины, уровень значимости

Ы. задан.

13.13.

Случайная

величинах

имеет нормальное

распреде-

ление .

Проверяется гипотеза

(Л

о против

аль-

тернативной гипотезы Hi :

на уровне значимости

оI =

- 0.05.

Сколько наблюдений необходимо, чтобы мощность

кри-

терия была не меньше

0.90?

§14. Интервальные

оценки параметров

нормального

распределения

14.I. 7

независимых равноточных измерений

жесткости

вала дали

резу.-ьтаты: 6.54; 6.38; 6.44; 6.51; 6.35; 6.47;

jfii Нести интервальную

оценку для

математического ожидания

"" |и, отвечающую уровню

доверия

95%,

считая ошибки изме-

[ИЙМ* нормальными.

|4 '. R результате 100

испытаний

обнаружено,

что

в сред-

Ни |*ftи

службы детали

составляет 10000 ч при среднеквадра-

Нципи отклонении 15ч. Найти

вероятность того, что

абсолют-

Ifjg ниокп в определении математического ожидания будет

Впцикг *>

и дисперсии -

меньше

I ч, считая,

что

срок

слул-

Я« цмIмпн • нормальная

случайная

величина.

* I'i.I. 8 независимых равноточных измерений коэффициекта

НЦвИшти лили результаты: 2.12; 2.34; 2.18; 2.25; 2.31; 2.Л;

m|U| П. Найти интервальную

оценку для

дисперсии коэффи-

11 и» 1111 • mi (Кости, отвечающую уровню

доверия

9С%,

считая

ошиб-

»н

и он р"пия

нормальными.

14,4. В результате 50

испытаний

обнаружено,

что

в сред-

; Н#" ИА

подготовку выстрела уходит

при среднеквадратич-

ны уклонении 1.2 с.

Построить интервальные оценки

для

матс-

H|tK4B<iKoi'()

ожидания

и дисперсии,

отвечающие

уровню доверия

читан,

что

время

для

подготовки

выстрела

- нормальная

Мучпйнаи величина.

§Т5.

Точечные

оценки

I I'i.I,

Пусть

число успехов

в 1Ъ независимых исгы-

tAii

• ч-

Бнрнулли, Р - вероятность

успеха

в одном испытании.

ИМму*

". методом

наибольшего правдоподобия оценить

параметр

, Показать,

что получанная

оценка является несмещзн-

Щ'И и

mi гнительной.

Г |9*2. По

выборке

Ki,... , Кц, объема fb методом наи-

iMIiiet o щшвдоподобия

оценить параметр

распределения Пуассо-

•14. ЦвКввать,

что

полученная

оценка является

несмещенной и

'II- |П4Тельной.

' l*i.J. ГЪ независимых измерений OCi,... величины

р получены

при

помощи ^ различных приборов. В предполо-

(»НИИ.

что

ОС{.

6 по измерениям

'1%, методом

наибольшего правдоподобия

найти оценку /л

Ннлн,

что

полученная

оценка является

несмещенной,и вычиг-

»*tI • лиеиерсию.

' l't.4. При

измерении давления были

получены следующие

1у«ьгяты: 3.12; 3.1; 2.9; 2.85; 3.17; 2.97; 3.08. Найти

•Нмвчшшие оценки математического

ожидания

и дисперсии дав-

|*НИ4.

имеет

место

15.5.

Пусть

•!,„., ft - независимые, одинако

распределенные

случайные

величины с

конечной дисперсией.

П<

зать,

что для любой оценки

среднего

причем

равенство достигается лииь при

u^st/h, , 1=

4,.,.,

15.6. Известно,

что

статистика

= г—тft) где

*^^^,

является

несмещенной

оценкой

минимальной дисперсией параметра

бпри неизвес

ном р . Показать,

что для

смещенной оценки

Л*-

параметра U справедливо неравенство

15.7.

Пусть

^ -

выборка объема

из

пуассоновокого

распределения К=С,1

... . Показать, что

не

существует

несмещенной

оценки

для

15.8. Выборочные значения Xj , 1 = описывают

си

равномерным

на интервале

(о,а) распределением. Методом

наибольшего правдоподобия найти оценку параметра

ОС. и пока

зать ее

достаточность.

15.S. Показать,

что

суммарное

количество

частиц

Ы(^) з

пуассоновской модели

излучения и

суммарное количество

части^

М tO

модели излучения радиоактивного распада

с распределе

нием по спектру энергий

= /((£)>0 2Г, dj^i

я /

J~i-

являются достаточными

статистиками

относительно

параметров

распределений и (см. задачи 12.2 и 12.4) .

§16.

Линейный анализ

регрессий

16.Т. Пусть Oi

и -

истинные веса двух

предметов

пусть (абсол.^)

ошибки

5"- взвеаивания случайны, независимы,

имеют о и "jbS't -S

; {.-=1,2.,... . Найти оценки

весов oii. и oIjl и

их дисперсии

для

каждой из

трех стратеги

взвешивания: