Pumping Station Desing - Second Edition by Robert L. Sanks, George Tchobahoglous, Garr M. Jones
Подождите немного. Документ загружается.

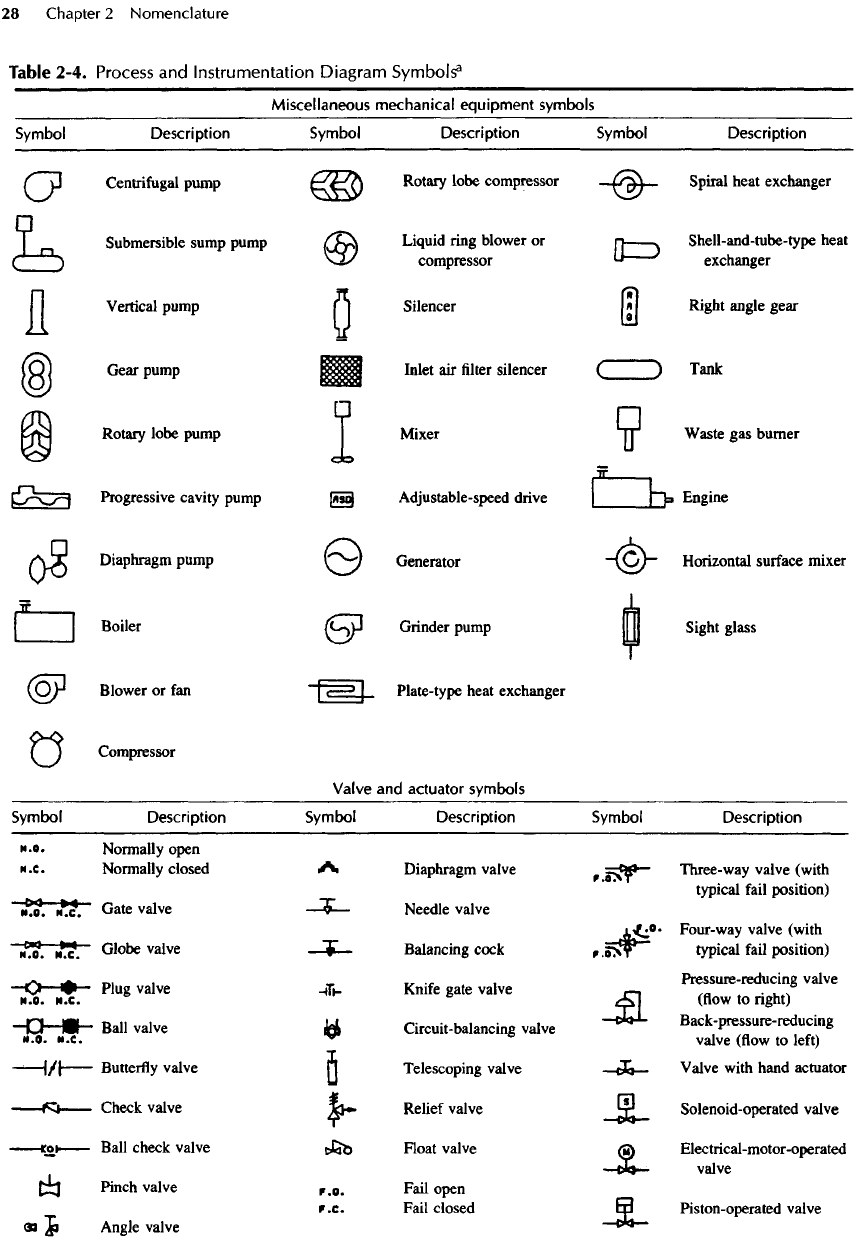
Table 2-4. Process
and
Instrumentation
Diagram
Symbols
3
Miscellaneous mechanical equipment symbols
Symbol
Description Symbol Description Symbol Description
Centrifugal
pump Rotary
lobe
compressorSpiral
heat exchanger
Submersible sump pump Liquid ring blower
orShell-and-tube-type
heat
compressorexchanger
Vertical pump
SilencerRight
angle gear
Gear pump Inlet
air
filter
silencerTank
Rotary lobe pump
MixerWaste
gas
burner
Progressive cavity pump Adjustable-speed
driveEngine
Diaphragm pump
GeneratorHorizontal
surface mixer
Boiler Grinder
pumpSight
glass
Blower
or fan
Plate-type heat exchanger
Compressor
Valve
and
actuator symbols
Symbol
Description Symbol Description Symbol Description
Normally
open
Normally
closed Diaphragm
valveThree-way
valve (with
typical
fail
position)
Gate
valveNeedle
valve
Four-way valve (with
Globe valve Balancing
cocktypical
fail
position)
™
,
T
_
..Pressure-reducing
valve
Plug
valve
Knife
gate
valve
/a
...
6
(flow
to
nght)
Ball
valve
Circuit-balancing
valveBack-pressure-reducing
valve
(flow
to
left)
Butterfly
valve Telescoping
valveValve
with hand actuator
Check valve Relief
valveSolenoid-operated
valve
Ball
check valve Float
valveEiectrical-motor-operated
valve
Pinch
valveFail
open
Fail
closedPiston-operated
valve
Angle
valve
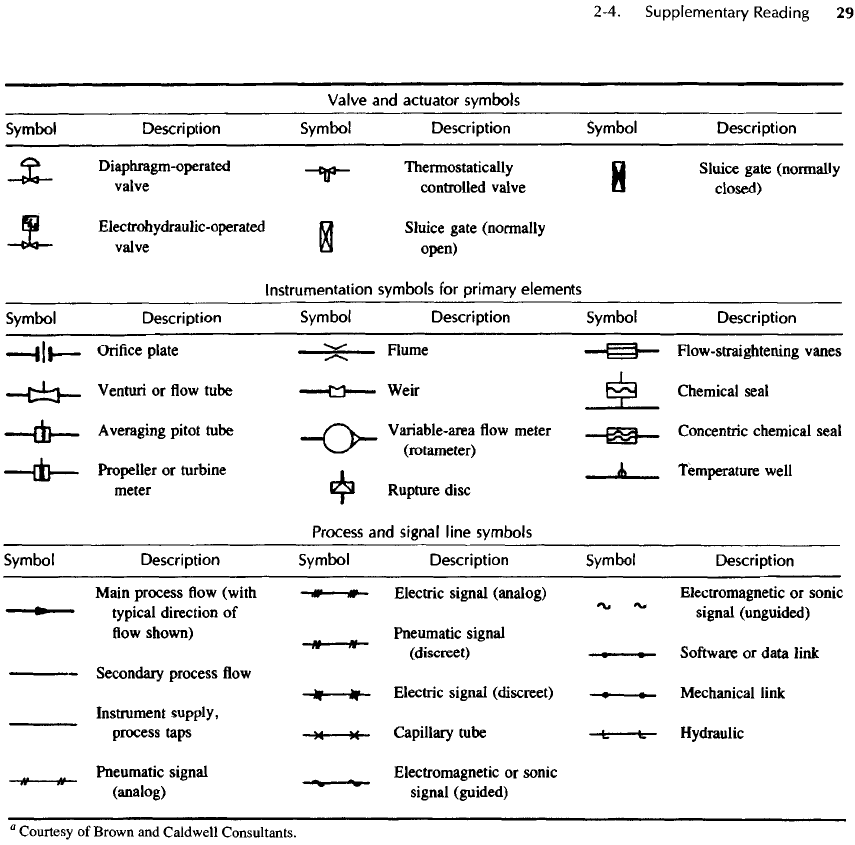
Valve
and
actuator
symbols
Symbol
Description Symbol Description Symbol Description
Diaphragm-operatedThermostaticallySluice
gate (normally
valvecontrolled
valve closed)
Electrohydraulic-operatedSluice
gate (normally
valve
open)
Instrumentation
symbols
for
primary
elements
Symbol
Description
Symbol
Description Symbol Description
Orifice
plateFlumeFlow-straightening
vanes
Venturi
or
flow
tubeWeirChemical seal
Averaging pitot
tubeVariable-area
flow
meterConcentric
chemical seal
(rotameter)
Propeller
or
turbineTemperature
well
meter Rupture disc
Process
and
signal line
symbols
Symbol
Description Symbol Description
Symbol
Description
Main
process
flow
(withElectric signal (analog)Electromagnetic
or
sonic
typical
direction
ofsignal
(unguided)
flow
shown)Pneumatic signal
(discreet)Software
or
data link
Secondary process
flow
Electric signal (discreet)Mechanical
link
Instrument
supply,
process
tapsCapillary
tube Hydraulic
Pneumatic signalElectromagnetic
or
sonic
(analog)
signal (guided)
a
Courtesy
of
Brown
and
Caldwell
Consultants.
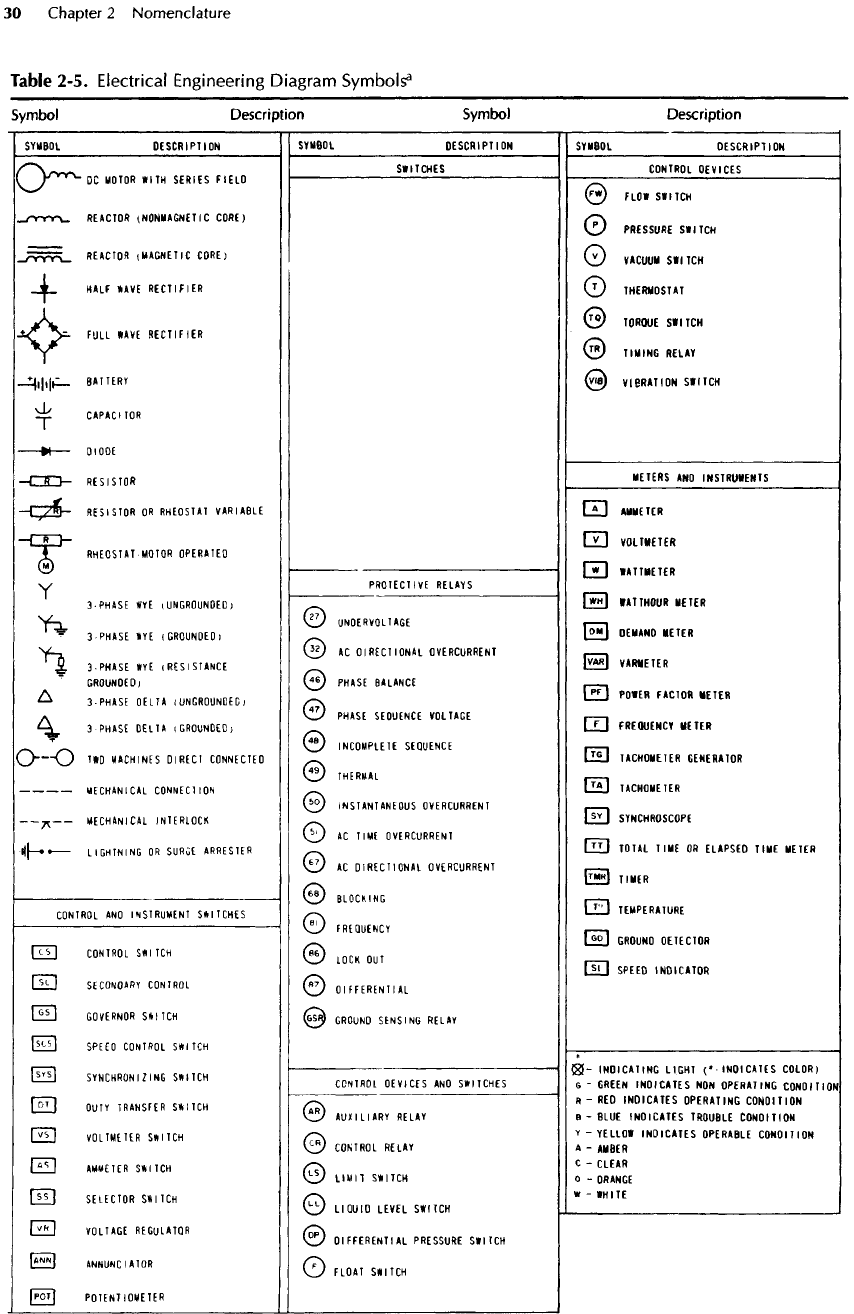
Table
2-5.
Electrical Engineering Diagram
Symbols
3
Symbol
Description
Symbol
Description
SYMBOL DESCRIPTION
SYMBOL
DESCRIPTION
SYMBOL
DESCRIPTION
SWITCHES
CONTROL
DEVICES
DC
MOTOR
WITH
SERIES FIELD
——
@
FLO*
SWITCH
REACTOR
(NONMAGNETIC
CORE)
S~\
\£J
PRESSURE
SWITCH
REACTOR
(MAGNETIC
CORE)
(7)
VACUUM
SWITCH
HALF
WAVE
RECTIFIER
(T)
THERMOSTAT
\*)
TORQUE
SWITCH
FULL
WAVE
RECTIFIER
^^^
(™)
TIMING RELAY
BATTERV
(vie)
VIBRATION SWITCH
CAPACITOR
0!ODE
RES(STOR
METERS
AND
INSTRUMENTS
RESISTOR
OR
RHEOSTAT
VARIABLE
I
*
1
AMMETER
I
vl
VOLTMETER
RHEOSTAT-MOTOR
OPERATED
f"*1
WATTMETER
PROTECTIVE
RELAYS
3-PHASE
WYE
(UNGROUNDED;
~~TT
t*3
WATTHOUR
METER
(^)
UNOERVOLTAGE
1
,
3-PHASE
WYE
(GROUNDED,
^
1™J
№**"<>
«'ER
Qf)
AC
DIRECTIONAL
OVERCURRENT
.
.
3-PHASE
WYE
(RESISTANCE
_^
I
VAR
I
VARMETER
GROUNDEDj
Gf)
PHASE BALANCE
,
.
3-PHASE
DELTA
(UNGROUNDED;
^
B
P
°
WER
FACT
°
R
«
T
"
\1I/
PHASE SEQUENCE
VOLTAGE
.
,
3
PHASE
DELTA
(GROUNDED)
LZJ
FREQUENCY METER
(^)
INCOMPLETE
SEQUENCE
,
,
TWO
MACHINES
DIRECT
CONNECTED
^-
LIlJ
TACHOMETER GENERATOR
(^)
THERMAL
,
,
MECHANICAL
CONNECTION
^^
LIlJ
TACHOMETER
(*°)
INSTANTANEOUS
OVERCURRENT
,
.
MECHANICAL
INTERLOCK
^
l_!LI
SYNCHROSCOPE
Ciy
AC
TIME
OVERCURRENT
LIGHTNING
OR
SURGE
ARRESTER
^.
LLlJ
TOTAL
TIME
OR
ELAPSED
TIME
METER
fc/
AC
DIRECTIONAL
OVERCURRENT
.
,
[™K|
TIMER
(**)
BLOCKING
j—T-j
CONTROL
AND
INSTRUMENT
SWITCHES
s~^
*-^-*
TEMPERATURE
v!V
FREQUENCY
.
,
-.^
I
60
I
GROUND
DETECTOR
ED
CONTROL
SWITCH
@
^
^
[
Si
]
SPEED
INDICATOR
QD
SECONDARY CONTROL
@
DIFFERENTIAL
EE
GOVERNOR
SWITCH
@
GROuND
SENSING
RaAy
l
scs
l
SPEED
CONTROL SWITCH
F^l
SYNCHRONIZING
SWITCH
~~
®~
INOICATING
UGHT
(*'INOlMTES
COLOR)
I
1
MNlHKUNUiNb
CONTROL
DEVICES
AND
SWITCHES
G -
GREEN
INDICATES
NON
OPERATING
CONDITION
ED
DUTY
TRANSFER
SWITCH
(^
R
"
RE
°
IN
°'
CMES
OP£R
*
TING
CONDIT
'°
N
O
1
AUXILIARY
RELAY
B-BLUE
INDICATES
TROUBLE
CONDITION
n/T]
VOLTMETERSWITCH
f^\
Y-YELLOWINDICATESOPERABLECONOlTION
(^)
CONTROL RELAY
A -
AMBER
I
AS
I
AMMETERSWITCH
fC^\
C-CLEAR
\^)
LIMIT
SWITCH
O -
ORANGE
1
SS I
SELECTORSWITCH
/TTN
W-WHITE
<ii/
LIQUID
LEVEL
SWITCH
J
El]
VOLTAGE REGULATOR
/O
VC/
DIFFERENTIAL
PRESSURE SWITCH
S
"NNWClAIO.
Q
fL04T
Sf|ICH
JPQTJ
POTENTIOMETER
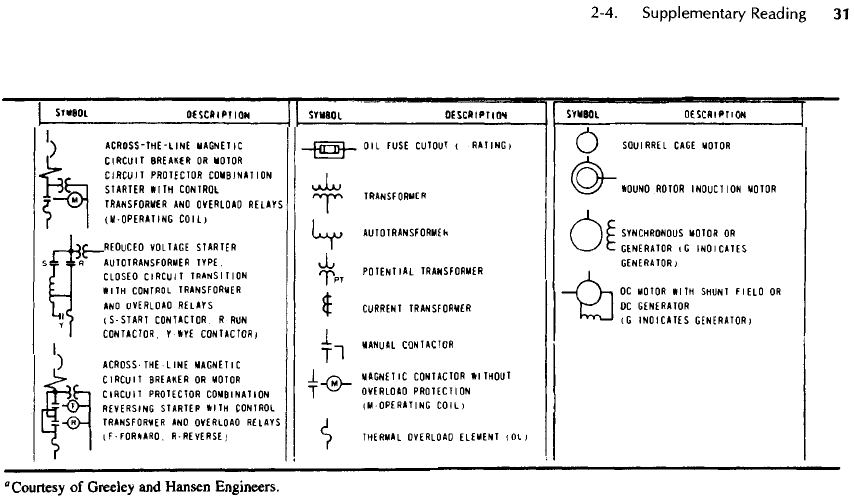
STMBOl
OCSCUIPTIQN
SmOl
OCSCRIPTIONSYMBOL
OCSCHlPTiQN
T
ACROSS-THE-LINE MAGNETICOIL FUSE CUTOUT
{
RATING)SQUIRREL CAGE MOTOR
CIRCUIT
BREAKER
OR
MOTOR
CIRCUIT
PROTECTOR COMBINATION
STARTER
*ITH
CONTROLTRANSFORMER»OUND
.ROTOR
INDUCTION MOTOR
TRANSFORMER
AND
OVERLOAD
RELAYS
(M-OPERATING
COIL)
AUTOTRANSFORMENSYNCHRONOUS
MOTOR
OR
.REDUCED
VOLTAGE STARTERGENERATOR
(G
INDICATES
AUTOTRANSFORMER
TYPE.GENERATOR)
CLOSED
CIRCUIT
TRANSITIONPOTENTIAL
TRANSFORMER
*ITH
CONTROL
TRANSFORMEROC
MOTOR
KITH
SHUNT
FIELD
OR
AND
OVERLOAD RELAYSCURRENT
TRANSFORMERDC
GENERATOR
(S-START
CONTACTOR
R
RUN(G
INDICATES
GENERATOR)
CONTACTOR.
Y
*YE
CONTACTOR)
MANUAL
CONTACTOR
ACROSS-THE
LINE
MAGNETIC
CIRCUIT
BREAKER
OR
MOTORMAGNETIC CONTACTOR
*ITHOUT
CIRCUIT
PROTECTOR
COMBINATIONOVERLOAD
PROTECTION
REVERSING
STARTEP
WITH
CONTROL(M-OPERATlNG COIL)
TRANSFORMER
AND
OVERLOAD RELAYS
(f-FOR*ARD.
R-REVERSE)
THERMAL OVERLOAD ELEMENT
(OL)
0
Courtesy
of
Greeley
and
Hansen
Engineers.
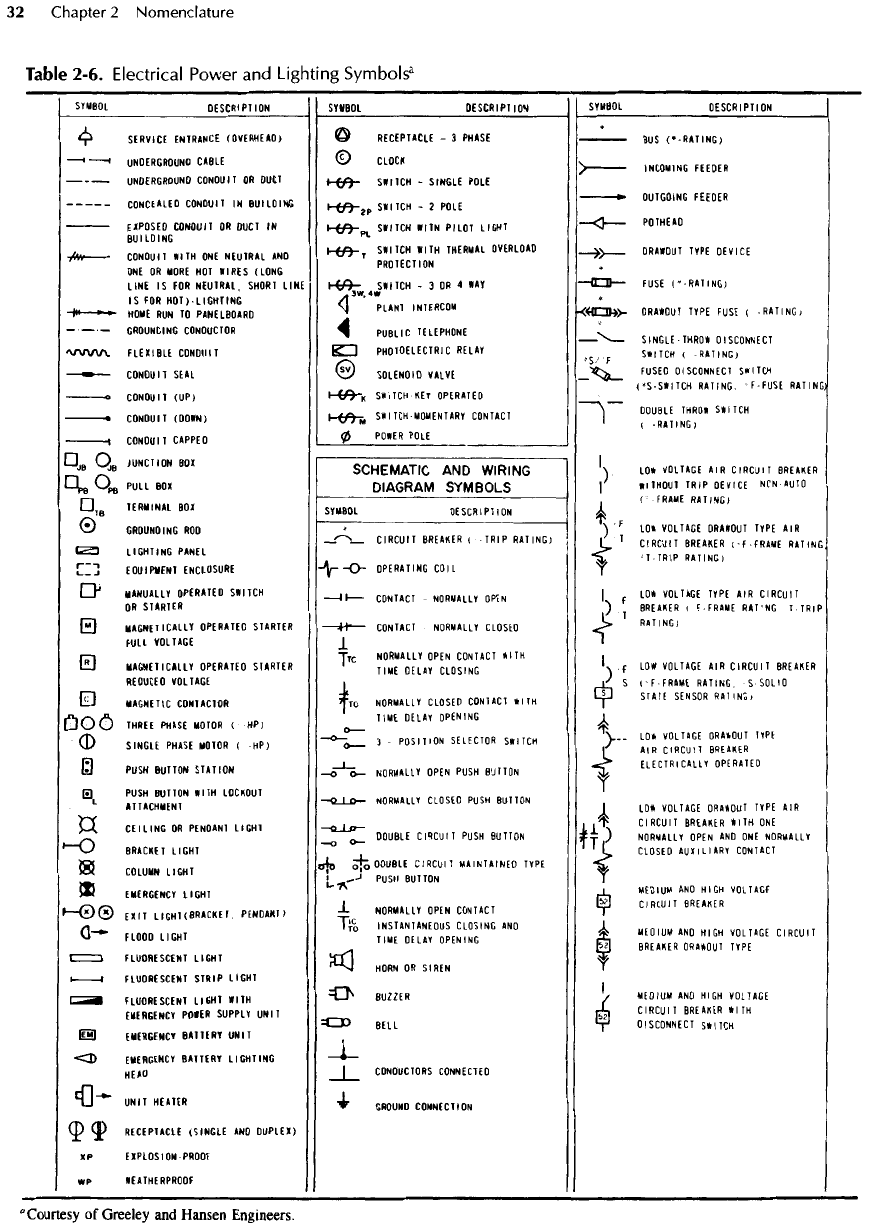
Table
2-6.
Electrical Power
and
Lighting
Symbols
3
SYM
BOL
DESCRIPTION
SYMBOL
DESCRIPTION
I I
SYMBOL
DESCRIPTION
SERVICE
ENTRANCE
(OVERHEAD)RECEPTACLE
- 3
PHASE
j
BUS
('.RATING;
UNKMMUNDCMUCLOC.
!,
NC
0«,
N
C
FtEDE*
UNDERGROUND
CONDUIT
OR
DUCTSWITCH
-
SINGLE POLE
CONCEALED
CONDUIT
IN
BUILDING^
SWITCH
- 2
POLEOUTGOING
FEEDER
EXPOSED
CONDUIT
OR
OUCT
INSWITCH
WITH
PILOT
LIGHTPOTHEAD
BUILDING
CONDUIT
W.TH
ONE
NEUTRAL
AND
S
*'
TCH
*'
TH
THERM
*
L
°
VERL
°
AD
™**^
TYPE
DEVICE
ONE OR
MORE
HOT
WIRES
(LONGPROTECTION
LINE
IS FOR
NEUTRAL,
SHORT
LINESWITCH
- 3 OR 4
WAYFUSE
("-RATING)
IS
FOR
HOT)-LIGHTING'*
,MTFRmM
HOME
RUN TO
PANELBOARDINItKLUMORAUfOUT
TYPE FUSE
(
-RATING,
GROUNDING CONDUCTORPUBLIC TELEPHONE
HJBUl
itLimuNtSINGLE-THRO*
DISCONNECT
FLEXIBLECONDUITPHOTOELECTRICRELAYSWITCH
(•-RATING)
CONDUIT
SEALSOLENOID
VALVE
FUSEO
DISCONNECT
SWITCH
(*S-SWITCH
RATING,
-
:
F-FUSE
RATING)
CONDUIT
(UP)SWITCH
KEY
OPERATED
CONDUIT
(DOWN)
SWITCH-MOMENTARY
CONTACT^1™*
"'^
CONDUIT
CAPPED
PO
*
ER
p
Dl£
|
JUNCTION
BOX
I
SCHEMATIC
AND
WIRING
ILO*
VOLTAGE
AIR
CIRCUIT
BREAKER
PULL
BOX
DIAGRAM
SYMBOLSWITHOUT
TRIP
DEVICE NCN-AUTO
TFRUlNAl
HfIX
(FRAME
RATING)
ItKMiNAL
BUA
SYMBOL
DESCRIPTION
GROUNDING
RODLOW
VOLTAGE
DRAWOUT
TYPE
AIR
UGHT(NG
pANEL
CIRCLIIT
BREAKER
<
-
TRIP
RA11NGJ
CIRCUIT
BREAKER
<-F-FRMIE
RATING
•'
T-TRIP
RATING)
EQUIPMENT
ENCLOSUREOPERATING
COIL
MANUALLY
OPERATED
SWITCH
CQNTACT
NOR||AUY
QPEN
LO*
VOLTAGE
TYPE
AIR
CIRCUIT
OR
STARTERBREAKER
i
F-FRAME
RAT'NG
T-TRIP
MAGNETICALLY
OPERATED STARTERCONTACT
NORMALLY
CLOSEDRATING)
FULL
VOLTAGE
NORMALLY
OPEN
CONTACT
*ITH
MAGNETICALLY
OPERATED
STARTER
T|ME
DELAy
CLO
SING
LOW
VOLTAGE
AIR
CIRCUIT
BREAKER
REDUCED
VOLTAGErF-FRAME
RATING.
S-SOUO
MAGNETIC
CONTACTORNORMALLY
CLOSED
CONTACT
*ITH
STA1E
SENSOR
RATING
'
THREE
PHASE
MOTOR
(HP)1.«
DElN
OPEHING
S.NGLE PHASE MOTOR
(
HP)3
-
POSIT.ON
SELECTOR
SW.TCH
L0
*
VOLTAGE
DRA
*
OL)T
Tm
blNbLt
HHAbt
MUlUN
(
-W)
fc|R
Q,
RCyn
BREAKER
PUSH
BUTTON
STAT.ON
NORMAUY
QPEN
PUSH
B
,
JTTON
ELECTRICALLY
OPERATED
PUSH
BUTTON
WITH
LOCKOUT
ATTACHMENT™™'^
CLOSED
PUSH
BUTTON^
^^
^^
^
^
CEILING
OR
PENDANT
LIGHT
C1RCU1T
BR
^KER
WITH
ONE
DOUBLE
CIRCUIT
PUSH BUTTONNORMALLY OPEN
AND
ONE
NORMALLY
BRACUU
LIGHTCLOSED
AUXILIARY
CONTACT
COLUMN
LIGHTDOUBLE
CIRCUIT
MAINTAINED
TYPE
PUSH
BUTTON
EMERGENCY LIGHTMEDIUM
AND
HIGH
VOLTAGF
EXIT
LIGHT(BRACKET.
PENDANT)NORMALLY
OPEN
CONTACT
CIRCUIT
BR£AK£R
INSTANTANEOUS
CLOSING
AND
FLOOD
LIGHT
T|ME
DELAy
OPEN|NG
MEDIUM
AND
HIGH
VOLTAGE
CIRCUIT
BREAKER
ORA»OUT
TYPE
FLUORESCENT
LIGHT
HORN
OR
SIREN
FLUORESCENT
STRIP
LIGHT
FLUORESCENT LIGHT
WITHBUZZERMEDIUM
AND
HIGH
VOLTAGE
EMERGENCY
POWER
SUPPLY
UNITCIRCUIT
BREAKER
WITH
BELLDISCONNECT
SWITCH
EMERGENCY BATTERY UNIT
EMERGENCY
BATTERY
LIGHTING
HEADCONDUCTORS
CONNECTED
UNIT
HEATERGROUND
CONNECTION
RECEPTACLE
(SINGLE
AND
DUPLEX)
XP
EXPLOSION-PROOF
WP
WEATHERPROOF
"Courtesy
of
Greeley
and
Hansen
Engineers.

Chapter
3
Flow
in
Conduits
ROBERT
L.
SANKS
CONTRIBUTORS
Appiah
Amirtharajah
Alfred
B.
Cunningham
William
F. H.
Gros
George
E.
Hecker
James
J.
McCormick
Rhys
M.
McDonald
Charles
D.
Morris
Dennis
R.
Neuman
Constantine
N.
Papadakis
Robert
E.
Phillips
Sanjay
P.
Reddy
Earle
C.
Smith
Thomas
M.
Walski
Gary
Z.
Watters
William
Wheeler
This chapter
is a
primer
for
those with little
or no
knowl-
edge
of
hydraulics
and a
review
for
those with more
experience. Even experts
may find
some
of the
material
(such
as
that dealing with pipe
flow
tables
and
formulas,
field
measurements
of flowrate and
friction coefficients,
and
the use of
tracers
or
models)
to be new and
useful.
Standards
and
specifications, such
as
ANSI
B36.10,
are
commonly (and
sufficiently)
identified
by the
call
number
and, hence,
are not
referenced
in
Section
3-14.
Double designations, such
as
ANSI/AWWA
104/
A21.4,
means that
AWWA
104 is the
same
as
ANSI
A21.4.
Titles
and
publishers
are
listed
in
Appendix
E.
Addresses
of
publishers
are
given
in
Appendix
F.
3-1.
Fundamentals
of
Hydraulics
The
analysis
of
water
flow in
closed
and
open con-
duits
depends
on
three fundamental
principles
—
the
conservation
of (1)
mass,
(2)
energy,
and (3)
momen-
tum.
Each
principle
is
considered
in
terms
of the
equation(s) derived
from
its
application.
Continuity
Equation
for
Mass
Based
on the
conservation
of
mass,
a
material balance
for
steady, continuous
flow in any
conduit means that
the flowrate of
material weight
in
equals
the flowrate
of
material weight out,
or
P
1
Q
1
=
p
2
2
2
-
constant
where
p is
density
and Q is flowrate or
discharge.
However,
Q
equals average velocity times cross-
sectional area,
and for
water
P
1
=
p
2
,
so
Q
=
A
1
V
1
=
A
2
V
2
=
constant (3-1)
Energy
Equation
Energy
per
unit
mass
in
flowing
water, expressed
in
kg •
m/kg
(or ft •
Ib/lb),
is the
summation
of
three
quantities:
•
Elevation head (potential energy) above
a
datum
(an
assumed level), usually termed
z and
expressed
in
meters
(or
feet);
•
Pressure head (also potential energy).
To put
this
into
the
same
units
as z
(elevation),
the
pressure
(p)
is
divided
by the
specific
weight
(y) and is
expressed
in
meters
(or
feet);
pressure head
is
shown
by the
height
to
which
the fluid
would rise
in a
piezometer
(an
open tube),
as
shown
in
Figure
3-1;
•
Velocity head (kinetic energy).
To put
this into
the
same
units
(meters
or
feet),
it is
expressed
as
V
2
^g,
where
v is
velocity
in
meters
per
second
(feet
per
second)
and g is
acceleration
due to
gravity,
9.81
m/s
2
(32.2
ft/s
2
).
In
equation form,
for
either open channels
or
closed
and
pressurized conduits,
the
total energy head
is
given
by
2
E
= z +
2
+
IL
(3-2)
Y
Ig
In
open channel
flow, if the
datum plane
is
taken
at the
invert
(bottom
of the
conduit)
and if the
invert
is
level,
z
becomes zero
and E is
defined
as the
specific
energy,
E
s
:
E
s
=
£
+
^
=
y
+
£
(3-3)
8
Y
Ig Ig
where
y is the
depth
of
water.
Conservation
of
Energy
The
energy
of
water
flowing
between
two
points
in
either
an
open channel
or a
closed conduit
is
derived
from
Equation
3-2 and
becomes
the
Bernoulli equa-
tion
2 2
77i
V
1
O
9
V
9
Z]
+
7
+
2^
=
Z2
+
7
+
2|
+
/if+I/l
™
(3
'
4)
where
h
f
is the
energy
per
unit mass dissipated
by
fric-
tion between points
1 and 2 and
Z/z
m
is the
summation
of
headlosses
due to
turbulence
in
pipe
fittings.
The
datum
plane
can be
assumed
at any
level
in
Equation
3-4
because
as z
increases,
p/j
decreases
by the
same
amount.
The
application
of
Equation
3-4 to
pipes
is
shown
in
Figure
3-1.
Note
how the
pressure head,
the
height
to
which water would rise
in a
piezometer
(an
open vertical tube), decreases
as the
velocity increases
(as it
must)
in the
smaller pipe.
Energy
and
Hydraulic
Grade
Lines
The
energy grade line
is a
plot
of the
energy head,
E
(as
defined
by
Equation 3-2),
vs.
horizontal distance.
In
Figure
3-1,
the
energy grade
line
drops both grad-
ually
(due
to
friction head
loss)
and in
steps (due
to
the
turbulence
in
bends
and
discontinuities).
The
pressure
at
point
1
forces
the
water
to
rise
in the
pie-
zometer.
A
pressure gauge
at
point
1
would read
P
1
,
which,
divided
by y, is the
pressure head
H
1
.
The
locus
of all
pressure head values
is the
hydraulic
grade
line
—
always
below
the
energy grade line
by
Figure
3-1.
Pipe,
piezometers,
and
energy
and
hydraulic
grade lines.

the
amount
of
velocity head,
v
2
/2g.
At
each bend
or
constriction
there
is a
small energy loss
due to
turbu-
lence.
At
expansions (point
8), the
energy
loss
is
sub-
stantially
greater. Even
if the
pipe were straight
and
prismatic
from
point
1 to
point
10,
there
would
be an
energy
loss
due to
friction
caused
by (1)
shear
at the
wall
and in the fluid and (2)
turbulence
due to
eddy
formation.
If the
velocity
in a
medium-sized
pipe
(300
mm or 12
in.)
is
less
than about 0.01
m/s
(0.03
ft/s),
there
is no
turbulence, friction depends only
on
shear,
and the flow is
called laminar
or
tranquil.
The
velocity
distribution
for
laminar
flow is
pictured
in
Figure 3-2a.
At the
velocities usual
in
pipes, there
are
secondary, crosswise currents that cause mixing,
the
flow is
turbulent,
and the
velocity distribution
across
a
pipe appears
as in
Figure
3-2b.
Between
laminar
and
turbulent
flow is a
transitional zone
where
the flow
might
shift
from
laminar
to
turbulent
and
back again
(or it
might
be a
combination
of
both).
The
pitot tube
in
Figure
3-1
penetrates
the
pipe
wall
and the
probe
is
bent with
its
open
end
facing
upstream.
In
this open
end of the
probe
of the
pitot
tube,
the
velocity
is
zero because there
is no flow in
the
tube.
But a
short distance upstream,
the
velocity
in
the
center
of the
pipe
is
v
c
.
Between that upstream
point
and the end of the
probe,
the
kinetic energy
head,
v
2
c
1
2g,
is
converted
to
potential
energy head
and
the
water
in the
tube rises
to the
energy grade line.
Actually,
the
water level
in the
pitot
tube
rises
slightly
above
the
energy line because
v
c
is the
maximum,
not
the
average, velocity.
An
average
of all
possible
pitot
tube
readings
from
wall
to
center would match
the
energy
grade line.
Momentum
Equation
The
force acting
on a
mass accelerates
it
according
to
Newton's third
law of
motion:
F
=
J(
7
V)
(3-5)
at
where
F is
force,
m is
mass,
v is
velocity,
and t is
time.
F and v are
vectors,
and F can be
considered
the
resultant (the
vectorial
sum)
of any
number
of
forces.
If
the
mass remains constant, then
F =
m^-
= ma
(3-6)
at
where
dv/dt
is
acceleration
in the
direction
of F. In
flowing
water,
it is
convenient
to
rearrange Equation
3-6 to
//v
F =
m^-
t
=
pQAv
=
PS(V
2
^v
1
)
(3-7)
where
F is the sum
(resultant)
of all
forces acting,
p is
mass density,
Q is flowrate or
discharge,
and the
arrow
sign indicates vectorial
subtraction
—
change
of
velocity.
A
force acting
on a
free
jet to
deflect
it is
applied
by
the
curved vane
in
Figure
3-3.
Vectorial subtraction
is
made
by
changing
the
sign
of
vector
PQv
1
then add-
ing
it
vectorially
(as
depicted
in
Figure
3-3b
or
3-3c)
to
obtain
F. The
reaction
of the jet
against
the
vane
is
equal
and
opposite.
The
momentum equation
is
needed
to find the
required strength
of
tie-downs, anchors,
and
thrust
blocks
to
restrain piping
at
elbows, tees, etc.
An
example
of the use of
Equation
3-7 is
given
in
Section 3-8.
3-2. Friction Losses
in
Pipe
The first
well-known formula
for flow in
pipes
was
proposed
by
deChezy.
The
deChezy
friction
coeffi-
cient
was
given
by a
complicated equation developed
Figure 3-2.
Velocity
profile
in a
300-mm
(12-in.)
pipe,
(a)
Laminar
flow;
(b)
turbulent
flow.

by
Kutter.
These
formulas
are no
longer
in
common
use.
The
Hazen-
Williams
(H-W) formula
has
been
used
in the
United States
for 90 yr. It is
simple
and
easy
to
use,
and it has
been
verified
by
many
field
observations
for
common sizes
of
pipes
at
conven-
tional
flowrates. The H-W
formula
is
essentially
required
by the
Ten-State Standards
[I].
Unfortu-
nately,
the
formula
is
irrational,
it is
valid only
for
water
at or
near room temperature
and flowing at
con-
ventional
velocities,
the flow
regime must
be
turbu-
lent,
and the C
factor varies with pipe size. These
disadvantages
seem
to be
generally ignored,
but
errors
are
appreciable
for
pipes less than
200 mm (8
in.)
and
larger than, say, 1500
mm (60
in.),
for
very cold
or hot
water,
and for
unusually high
or low
velocities.
Never-
theless,
its
continuous
use has
engendered
a
nearly
blind
faith
in it.
The
Manning equation (Section 3-5)
is
somewhat
similar
to the H-W
formula
and is
subject
to the
same
limitations.
It is
widely used
in the
United
States
for
open channel
flow,
such
as
pipes that
are
partly
full.
Sometimes
it is
used
for
full
pipes,
but for
this
application
it has no
advantage over
the H-W
formula.
The
Colebrook-
White
equation
is
more accurate
than
the H-W
formula
and is
applicable
to a
wider
range
of flow,
pipe size,
and
temperature.
It is
widely
used
in the
United Kingdom
and
elsewhere
in
Europe.
The
Darcy-Weisbach equation
is the
only rational
formula,
and it is
applicable
to
turbulent, laminar,
or
transitional
flow, all
sizes
of
pipe,
and any
incom-
pressible Newtonian
fluid at any
temperature.
It has
not
been popular because, being
an
implicit equation,
it
must
be
solved
by
successive trials.
It was
therefore
inconvenient
to
use,
but
now, modern computers (even
programmable
pocket calculators)
can be
used
to
solve
the
equation
in
seconds.
In
this
text, only
the
H-W, Manning,
and
Darcy-
Weisbach
equations
are
discussed. Benedict
[2] has
discussed
formulas
for
pipe
flow
extensively.
Hazen-Williams
Equation
The
Hazen-Williams
equation, developed
from
exten-
sive reviews
of
data
on
pipes
installed
all
over
the
world,
was
made public
in
1905
[3].
The
appeal
of the
equation
is due
partly
to its
simplicity
and
ease
of
use,
partly
to the
source
of the
data (real pipes
in the
field
—
not
just laboratory pipes), and,
by
now,
to a
tra-
dition
of
nearly
a
century
of use and
faith
in the
results.
The
original
form
of the
Hazen-Williams
equation
[3] was
developed
in
U.S. units.
In SI
units,
the
equation
is
v
=
0.849Cfl°-
63
S°-
54
(3-8a)
where
v is
velocity
in
meters
per
second,
C is a
coeffi-
cient
ranging
from
about
80 for
very rough pipes
to
150 or
more
for
smooth pipes,
R is the
hydraulic
radius
in
meters,
and S is the
friction
headloss
per
unit
length
or
slope
of the
energy grade line
in
meters
per
meter.
The
hydraulic radius
is
defined
as the
water
cross-sectional area divided
by the
wetted penmeter.
For
full
pipes,
R
reduces
to
D
/4
where
D is the ID.
In
U.S. customary units,
the
equation
is
v
=
1.318Cfl°-
6
Y-
54
(3-8b)
where
v is in
feet
per
second,
R is in
feet,
and S is in
feet
per
foot.
Friction
headloss
is
expressed
more conveniently
as the
gradient,
/z
f
,
in
meters
per
1000
m
(or
feet
per
1000
ft)
instead
of S.
Velocity
can
also
be
expressed
as
discharge,
<2,
divided
by
water cross-sectional area,
A.
Substituting
and
rearranging Equation
3-8
yields
another, somewhat more convenient
form.
In SI
units,
*,
-
(,0,70o(§)
L<
y»
.
(^C)"
«3-9a,
where
h
f
is
meters
per
1000
m, Q is
cubic meters
per
second,
and D is
pipe diameter
in
meters. Values
of C
are
given
in
Table
B
-5
(Appendix
B).
Figure
3-3.
Impulse
momentum,
(a)
Schematic
diagram;
(b)
vector
diagram;
(c)
equivalent
vector
diagram.

Equation
3-9a,
expressed
in
U.S.
customary units,
is
.,
-
(IWOO®'
V"
. (
»;
2
e)"
S
(3-
9b
)
where
h
f
is
feet
per
1000
ft, Q is
gallons
per
minute,
D
is
pipe diameter
in
inches,
and C,
again,
is
given
in
Table
B-5
(Appendix
B).
See
Subsection
"Friction
Coefficients"
for a
dis-
cussion
of the H-W C
factor.
Darcy-Weisbach
Equation
The
equation
for
circular pipes
is
*
=
/Z^
(3-10)
where
h is the
friction
headloss
in
meters
(feet),
/is
a
coefficient
of
friction
(dimensionless),
L is the
length
of
pipe
in
meters
(feet),
D is the
inside
pipe
diameter
in
meters
(feet),
v is the
velocity
in
meters
per
second
(feet
per
second),
and g is the
acceleration
of
gravity,
9.81
m/s
2
(32.2
ft/s
2
).
The
advantages
of the
Darcy-
Weisbach equation
are as
follows:
• It is
based
on
fundamentals.
• It is
dimensionally consistent.
• It is
useful
for any fluid
(oil, gas, brine,
and
sludges).
• It can be
derived analytically
in the
laminar
flow
region.
• It is
useful
in the
transition region between laminar
flow and
fully
developed turbulent
flow.
• The
friction
factor
variation
is
well documented.
The
disadvantage
of the
equation
is
that
the
coeffi-
cient
/
depends
not
only
on
roughness
but
also
on
Reynolds
number,
a
variable that
is
expressed
as
R
=
v
-»
(3-11)
V
where
R is
Reynolds number (dimensionless),
v is
velocity
in
meters
per
second
(feet
per
second),
D is
the
pipe
ID in
meters
(feet),
and V is
kinematic viscos-
ity
in
square meters
per
second (square
feet
per
sec-
ond)
as
given
in
Appendix
A,
Tables
A-8 and
A-9.
Determination
of
f
In
the
laminar
flow
region where
R is
less than
2000,/
equals
64/
R
and is
independent
of
roughness.
Between Reynolds numbers
of
2000
and
about
4000,
flow is
unstable
and may fluctuate
between laminar
and
turbulent
flow, so / is
somewhat
indeterminate.
When
R is
very large (greater than about
10
5
),
the
flow is
fully
turbulent
and
/depends
only
on
rough-
ness.
In the
transition zone between turbulent
and
laminar
flow,
both roughness
and R
affect/, which
can
be
calculated
from
a
semianalytical expression devel-
oped
by
Colebrook
[4]:
1
Oi
(zlV
,
2.5l}
n
1T
.
jf-
-
210
H
3
-
7
v/J
(
}
where
e is the
absolute roughness
in
millimeters
(or
inches
or
feet)
and D is the
inside diameter
in
millime-
ters
(or
inches
or
feet),
so
that
z/D
is
dimensionless.
The
Moody diagram, Figure
B-I
(Appendix
B), was
developed
from
Equation
3-12
[5].
Note that
the
curves
are
asymptotic
to the
smooth-pipe curve
(at the
left).
To the right,
curves calculated
from
the
Cole-
brook (also
called
Colebrook-White)
equation
are
indistinguishable
from
the
horizontal lines
for
fully
developed turbulent
flow
given
in
Prandtl
[6].
The
probable variation
of
/
for
commercial pipe
is
about
±10%,
but
this variation
is
masked
by the
uncertainty
of
quantifying
the
surface roughness.
An
explicit,
empirical equation
for
/was
developed
by
Swamee
and
Jain
[7]:
/ =
—
2
(3-13)
,
(e/D
5.14]
10gl
{37
+
^J
The value
of
/calculated
from
Equation
3-13
differs
from
/calculated
from
the
Colebrook equation
by
less
than
1%.
Friction headloss
can be
determined
from
the
Darcy-Weisbach
equation
in a
number
of
ways:
• Use one of the
Appendix tables
(B-I
to
B
-4)
to find
the
appropriate pipe size. Compute
R, find
/from
the
Moody diagram,
and
compute
an
accurate value
of h
from
the
Darcy-Weisbach equation. Because
/
changes only
a
little
for
large changes
of R, no
second
trial
is
needed. Compare
the h so
obtained with
the
value
in
Tables
B-I
to
B
-4
for an
independent check.
•
Program
Colebrook's
Equation 3-12
to find
/as
an
iterative subroutine
for
solving Equation
3-10
with
a
computer. Once programmed
(a
simple task even
for
a
hand-held, card-programmable calculator),
any
pipe problem
can be
solved
in a few
seconds.
• Use the
Swamee-Jain
expression
for / in the
Darcy-Weisbach
equation. Equation
3-13
could
even
be
used
as a first
approximation
for
iteration
of
Equation
3-12.
•
Refer
to the
extensive tables
of flow by
Ackers
[8].
