Пташкина-Гирина О.С.; Щирый В.Д. Гидравлика. Учебное пособие
Подождите немного. Документ загружается.

91
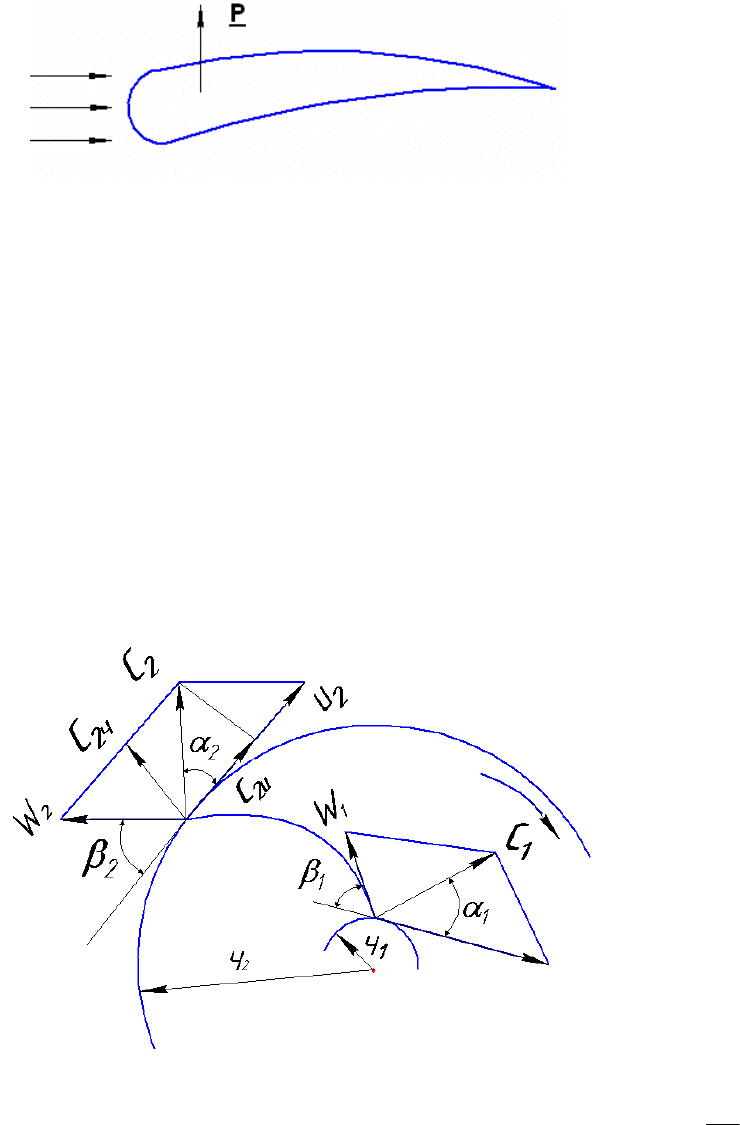
вихревая (теория Н.Е. Жуковского). Суть ее заключается в том,
что лопасть рабочего колеса, при обтекании которого возникает
подъемная сила, заставляющая перемещать жидкость внутри ко-
леса (рис.10.2)
Рис.10.2
Вихревая теория более приемлема для объяснения работы
осевых насосов и менее удобна для центробежных.
Вторая – струйная (теория Л.Эйлера). Суть этой теории за-
ключается в том, что сложное движение жидкости внутри рабо-
чего колеса насоса идеализируется и принимается строго упоря-
доченным – струйным. Для этого рабочее колесо должно иметь
бесконечно большое число бесконечно тонких лопастей.
Для такого упорядоченного движения жидкости можно
представить параллелограммы скоростей на входе и выходе ло-
пастей (рис.10.3) с индексами «1» - на входе и «2» - на выходе.
Для этого выделим только одну лопасть (рис.10.3).
Рис.10.3
При вращении рабочего колеса с угловой скоростью
30
n
π
=Ω
жидкость приобретает переносную скорость U, направленную
касательно к окружностям радиусов r
1
и r
2
: U = Ωr. При бесконеч-
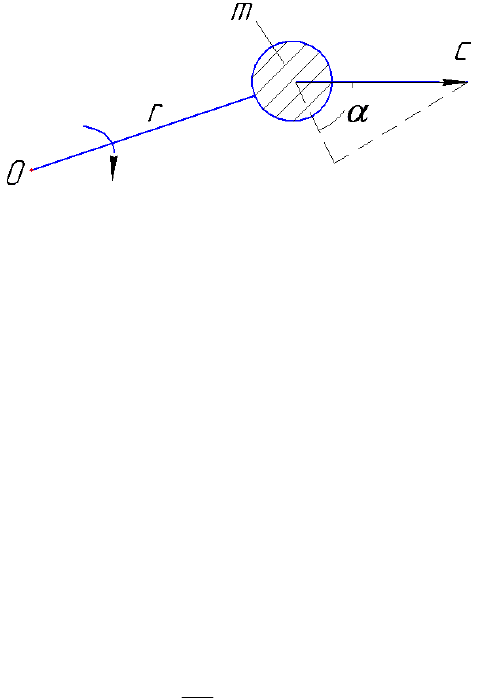
92
но большом числе лопастей траектория каждой струйки будет
соответствовать профилю лопасти, поэтому под действием цен-
тробежной силы каждая частица жидкости относительно и каса-
тельно к лопасти приобретает относительную скорость W. Угол
между относительной скоростью и обратным направлением пе-
реносной скоростью называют углом наклона лопастей β
1
и β
2
.
Для вывода основного уравнения центробежного насоса
воспользуемся теоремой механики об изменении момента коли-
чества движения для движущейся жидкости, которую в этом слу-
чае можно сформулировать так:
Изменение момента количества движения массы жидко-
сти в единицу времени относительно оси вращения рабочего
колеса равно сумме моментов всех внешних сил относитель-
но той же оси, т.е. крутящему моменту.
Иллюстрация теоремы представлена на рис.10.4.
Рис. 10.4
В потоке жидкости, сходящей с лопастей рабочего колеса
центробежного насоса, происходит непрерывное увеличение мо-
мента количества движения в результате также непрерывного
подвода к жидкости механической энергии от двигателя, вра-
щающего рабочее колесо.
Целью вывода указанного уравнения является получение
уравнения напора, развиваемого центробежным насосом.
Рассмотрим элементарную струйку, движущуюся вдоль ло-
пасти рабочего колеса насоса.
Моменты количества движения струйки:
на выходе из колеса
222
'
2
rcosC
g
q
М ⋅α
γ
=
;
на входе в колесо

93
1
r
1
сosб
1
C
g
гq
1
M =
′
.
Изменение момента количества движения
( )
111222
rcosCrcosC
g
q
М ⋅α−⋅α
γ
=
′
∆
.
Для всей совокупности струек Q = Σq; Σ∆М` = М. Тогда
( )
111222
rcosCrcosC
g
Q
М ⋅α−⋅α
γ
=∆
.
Так как
Ω
=
N
М
; N =
∞
γ
т
QH
,
∞
γ
т
QH
=
( )
111222
rcosCrcosC
g
Q
⋅α−⋅α
γ
Ω
.
Так как Ω·r=U, то
(
)
1
сosб
1
C
1
U
2
сosб
2
C
2
U
g
1
Н
Т
−=
∞
. (10.1)
При проектировании центробежных насосов угол α
1
=90°, т.е.
отсутствует предварительная закрутка жидкости; тогда
g
2
сos
б
2
C
2
U
Н
Т
=
∞
. (10.2)
Так как С
2
·сosα
2
=C
2u
, то
g
CU
Н
u22
т
=
∞
. (10.3)
Из параллелограмма скоростей следует, что
2
r
2
2
u
2
ctgCUC
β
−
=
; с учетом этого можно записать
(
)
2r22
2
2
т
ctgCUU
g
1
H β⋅+=
∞
. (10.4)
Каждая в отдельности зависимость (10.1, 10.2, 10.3, 10.4) яв-
ляется основным уравнением центробежного насоса, из которого
следует основной вывод, что развиваемый напор не зависит от
рода перекачиваемой жидкости.
В действительности такой напор насос развить не может, так
как число лопастей у реального насоса не бесконечное, а конеч-
ное. В этом случае мгновенной передачи механической энергии
жидкости не произойдет. Учитывается этот факт коэффициентом
ε=0,7…0,9.

94
Теперь уже в реальном насосе с конечным числом лопастей
произойдут гидравлические потери
95,0...9,0
г
=
η
вследствие вих-
реобразования при движении жидкости в рабочем колесе, а также
в результате недостаточно плавного входа потока на рабочее ко-
лесо (потери на удар при входе) и, наконец, в результате трения
жидкости о лопасти и стенки корпуса насоса.
Таким образом, аналитическое выражение действительного
напора реально насоса имеет вид
g
CU
Н
u22
г
εη=
. (10.5)
Из уравнений (10.1 - 10.5) следует, что развиваемый центро-
бежным насосом напор зависит в основном от двух факторов:
частоты вращения колеса и его диаметра. Для цели получения
большего напора тот и другой путь весьма ограничен, поэтому
для достижения более высокого напора насосы выполняют мно-
гоступенчатыми, когда на одном валу могут быть смонтированы
от двух до нескольких сот рабочих колес.
10.1.3. Подача центробежного насоса
Представим схематически рабочее колесо центробежного
насоса (рис.10.5).
Рабочее колесо насоса наружным диаметром D
2
жидкость
покидает с радиальной составляющей абсолютной скорости С
2r
через окна, образованные лопастями шириной b
2
. С учетом
уменьшения (стеснения) лопастями пространства между дисками
колеса теоретическая подача
Q
T
=
r
2
2
2
СbD
⋅
ϕπ
, (10.6)
где
ϕ
- коэффициент загромождения, учитывающий толщину ло-
пастей,
ϕ
=0,87…0,92.
Рис.10.5
95
Действительная подача с учетом объемных потерь будет не-
сколько меньше:
Q=
Т
о
Q
η
,
где
о
η
- объемный к.п.д,
о
η
=0,95…0,98.
10.1.4. Теоретические характеристики центробежного насоса
Характеристикой насоса называется зависимость напора от
подачи при постоянной частоте вращения рабочего колеса:
Н
Т
∞
= f(Q)
Т
.
Из выражения (10.6) определим радиальную составляющую
абсолютной скорости:
2
2
2
T
r2
bD
Q
С
πϕ
=
и подставим ее в выражение (10.4):
T
Q
2
b
2
рD
2
g
2
ctgв
2
U
g
2
2
U
T
Н
ϕ
−=
∞
. (10.7)
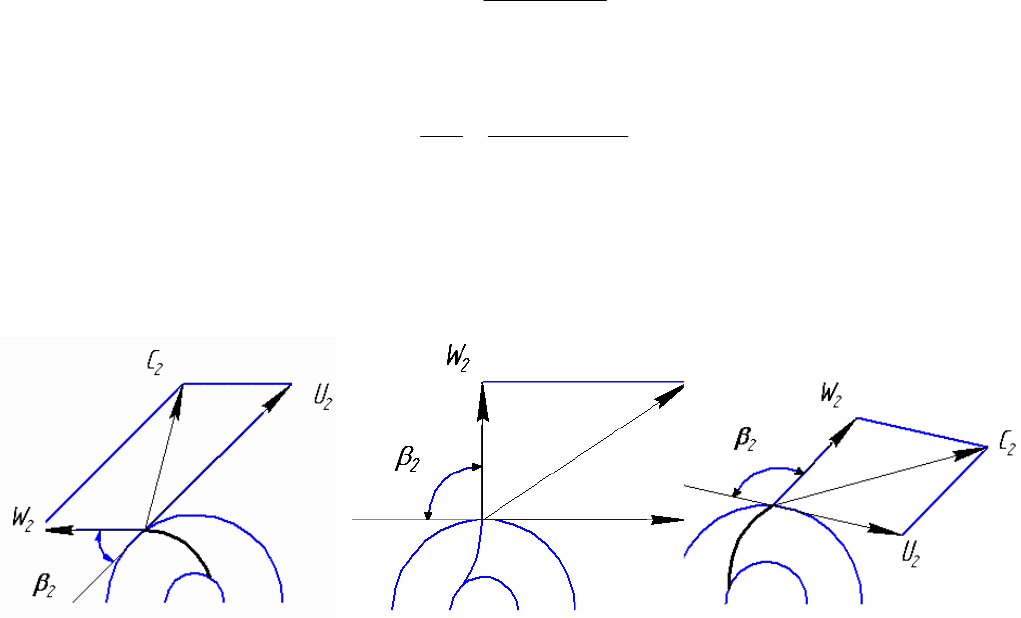
Из выражения (10.7) следует, что теоретическая характери-
стика центробежного насоса зависит от характера изогнутости
лопасти на выходе из рабочего колеса (угол β
2
) (рис.10.6).
β β
2
<90
о
β
2
=90
о
β
2
>90
о
Рис. 10.6
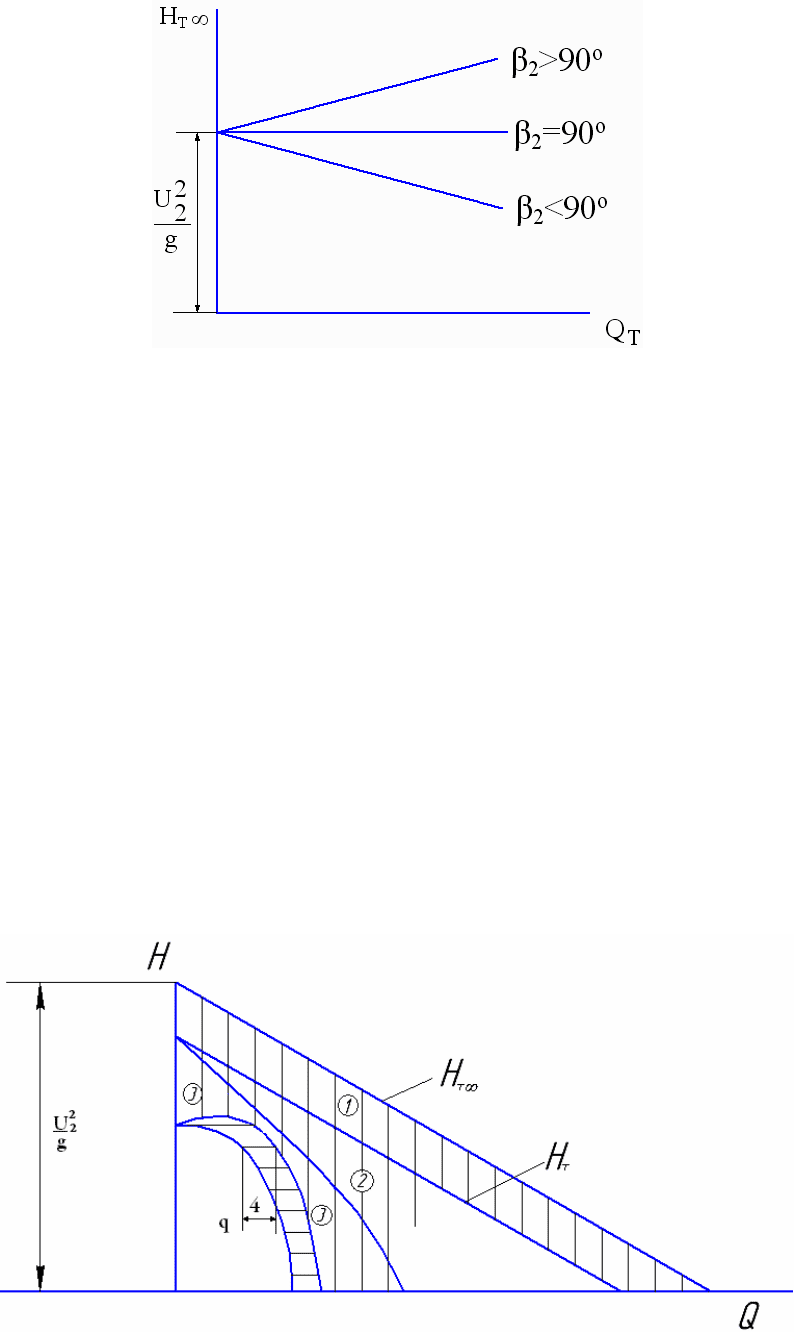
Эти характеристики представлены на рис. 10.7.
Установлено, что оптимальными к.п.д. обладают рабочие
колеса, у которых угол наклона лопастей на выходе β
2
=14-50
о
,
т.е. значительно меньше 90
о
.
96
Рис.10.7
10.1.5. Действительная характеристика центробежного наоса
В предыдущем разделе мы рассматривали работу по идеаль-
ного центробежного насоса, т.е. насоса с бесконечно большим
числом лопастей и коэффициентом полезного действия, равным
единице. Чтобы приблизиться теперь к рабочему процессу реаль-
ного насоса, отбросим сначала первое из принятых допущений,
оставив в силе второе, т.е. число лопастей конечное.
Обычно на практике число лопастей составляет от шести до
двенадцати. В этом случае относительное течение в межлопаст-
ных каналах колеса уже не является таким струйным, как пред-
полагалось ранее, и поэтому приводит к потере напора (1)
(рис.10.8).
Рис. 10.8
97
При работе насоса с конечным числом лопастей происходят
гидравлические потери (2), которые из-за турбулизации жидкости
пропорциональны скорости во второй степени.
Центробежный насос спроектирован и изготовлен с таким
расчетом, что максимальное значение его к.п.д. соответствует оп-
тимальной подаче Q
опт
. Это означает, что относительная скорость
на входе в рабочее колесо W
1
касательна к кривизне лопасти.
Этим обеспечивается безударный вход жидкости в рабочее коле-
со. Работа насоса при Q
опт
может осуществляться только случай-
но. При эксплуатации же реальная подача Q
опт
< Q< Q
опт
и поэто-
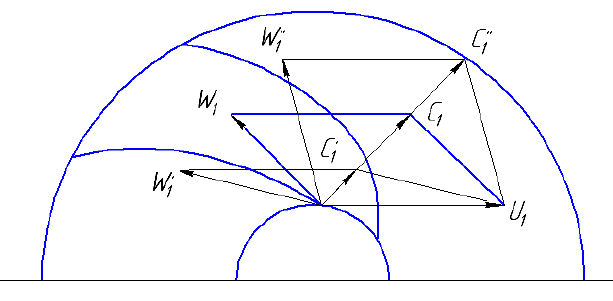
му удар на входе неизбежен. Это видно из параллелограммов
скоростей (рис.10.9).
Рис. 10.9
На рис.10.8 потери на удар обозначены позицией 3.
В реальном насосе происходит утечка жидкости (4) из об-
ласти высокого давления в область низкого. Утечки приводят к
сдвигу кривой напоров влево на величину утечек q.
Таким образом, действительная характеристика насоса име-
ет вид кривой второго порядка.
Приведенные выше рассуждения являются приближенными,
так как они не учитывают ряд факторов, влияющих на напор и
мощность. Поэтому характеристики на основании описанных
рассуждений плохо согласуются с данными опыта. Действитель-
ная характеристика насоса может быть получена лишь опытным
путем на основании его стендового испытания. При этом, кроме
характеристики Н = f(Q), получают еще N = f(Q),
η
= f(Q) и
доп
вак
Н
= f(Q) при частоте вращения n.
98
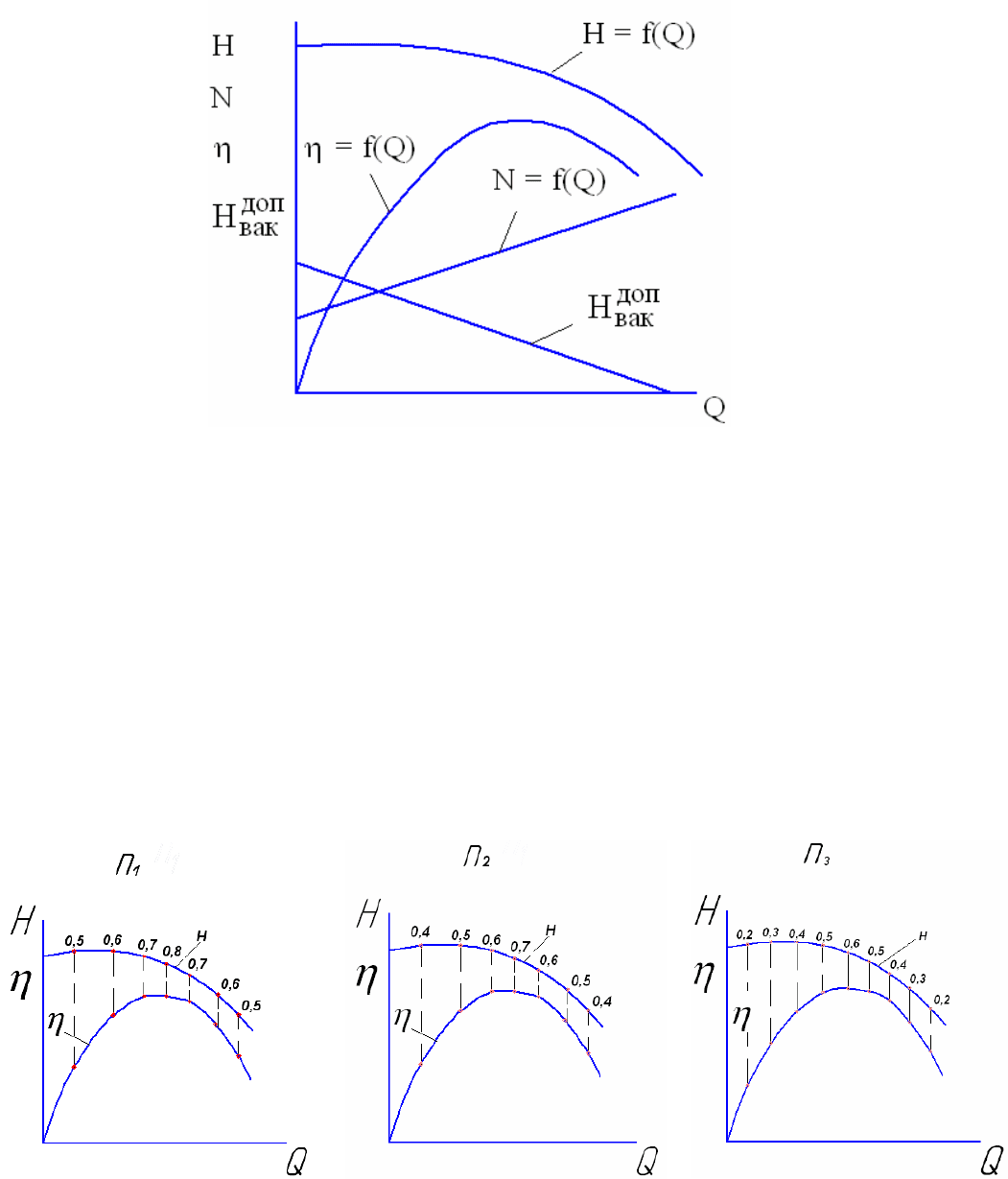
Характер указанных зависимостей представлен на рис.
10.10. В результате анализа этих зависимостей можно составить
полное представление о работе насоса и произвести его подбор
для конкретных условий.
Рис. 10.10
10.1.6. Универсальные характеристики центробежного насоса
Для уточнения оптимальной частоты вращения насоса опре-
деленной серии производят его испытания при различных часто-
тах вращения рабочего колеса, например, при n
1
, n
2
и n
3
с по-
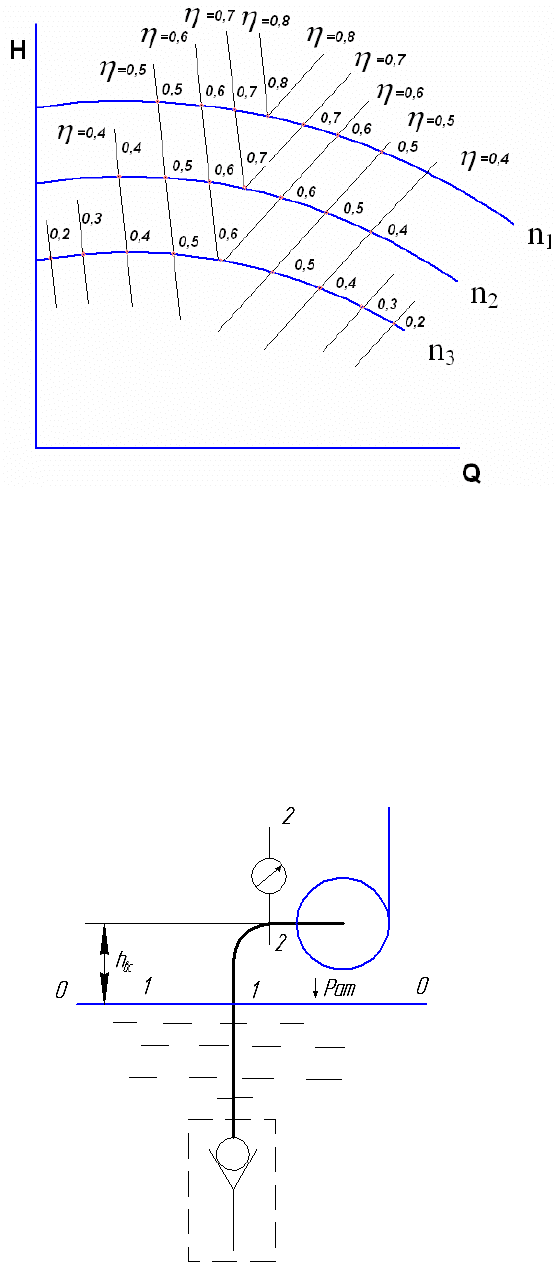
строением зависимостей Н = f(Q) и
η
=f(Q) и переносом к.п.д. на
кривые зависимостей Н = f(Q) (рис.10.11). Затем на один график
переносят кривые Н = f(Q) с отметками значений к.п.д.
Рис. 10.11
99
Одинаковые значения к.п.д. соединяют тонкими линиями
подобно горизонталям на топографических картах (рис.10.12).
Рис. 10.12
10.1.7. Процесс всасывания и явление кавитации
в центробежном насосе
Рассмотрим наиболее распространенный случай работы
центробежного насоса, когда он установлен выше уровня жидко-
сти, находящейся под атмосферным давлением (рис. 10.13).
Рис. 10.13
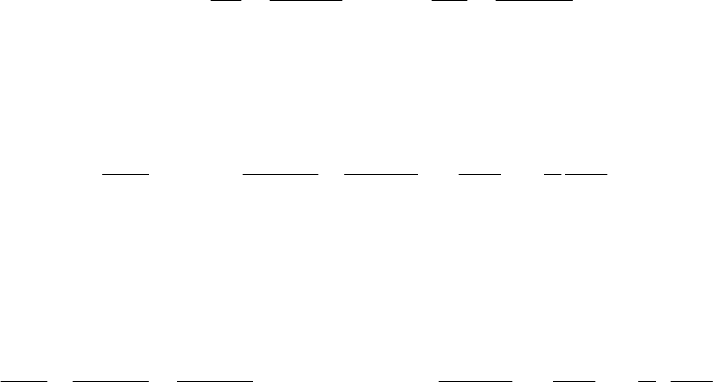
100
Расстояние по вертикали от поверхности жидкости до оси
насоса называют высотой всасывания h
вс.
Составив уравнение Бернулли для сечения 1-1, взятого по
поверхности жидкости, и сечения 2-2 на входе, где установится
давление ниже атмосферного, относительно плоскости сравнения
0-0, совпадающего с сечением 1-1.
Расчетная форма уравнения Бернулли для потока реальной
жидкости, как известно, имеет вид
п
2
222
2
2
111
1
h
g2
Vp
z
g2
Vp
z +
α
+
γ
+=
α
+
γ
=
.
После его анализа для выбранных сечений это уравнение можно
записать в виде
g2
2
2
V
d
л
g2
2
2
V
ж
g2
2
2
V
2
б
г
абс2
p
вс
h
г
ат
p
l
++++=
,
где ζ – суммарный коэффициент местных потерь (обратный кла-
пан, сетка, различные повороты и т.д.).
Выполним элементарное преобразование:
g2
2
2
V
б
л
g2
2
2
V
ж
g2
2
2
V
2
б
вс
h
вак
Н
г
вак
2
p
г
абс2
p
г
ат
p
⋅+++===−
l
. (10.8)
Когда абсолютное давление на входе в насос становится
меньше или равным давлению насыщенного пара (р
2 абс
≤
.
п
н
абс
р
)
перекачиваемой жидкости, что соответствует предельно допус-
тимому вакууму (
доп
вак
Н
), жидкость мгновенно вскипает, т.е. пре-
вращается в пузырьки пара. Перемещаясь далее в межлопастном
пространстве к периферии рабочего колеса, они конденсируются
ввиду повышения давления. Процесс образования пузырьков и их
конденсации называется кавитацией (от латинского «каверна»,
что означает «пустота»). В рассматриваемом случае кавитация
будет гидродинамической. Скоростной киносъемкой (2 млн 250
тыс. кадров в секунду) установлено, что в течение 1 с на площади
лопасти 1 см
2
образуется порядка 30·10
6
пузырьков.
В момент конденсации пузырька происходит местное повы-
шение давления (до 3500 атмосфер) и температуры (1000-1200º
С), и если пузырек задерживается на лопасти, произойдет ее раз-
рушение. В разрушении участвует один из 30·10
3
образовавшихся
