Prinz H. Numerical Methods for the Life Scientist
Подождите немного. Документ загружается.

triliganded, etc. occupation. If we know the intrinsic affinities of each individual
binding site at each step, we can compute the simplified affinities of a sequential
scheme. This reasoning does not work in the opposite direction: Since equilibrium
binding studies can only determine one effective equilibrium dissociation constant
for the different occupation of sites, intrinsic equilibrium dissociation constants for
the different sites cannot be deduce d without further assumptions.
Only if we assume that affinities of all n individual binding sites are equivalent,
can intrinsic equilibrium dissociation constants K
D
i
intrinsic
for the ith steps be
calculated from the effective (seq uential) equilibrium dissociation constants (2.30).
K
D
i
intrinsic
¼ ((n i þ 1)/i) K
D
i
sequential
(2.30)
As an example, let us assume two step sequential binding sites with K
D
1
sequential
¼
K
D
2
sequential
¼ 10 mM according to reaction scheme (2.18). These equilibrium disso-
ciation constants of scheme (2.18) translate to K
D
1
intrinsic
(¼K
D
2
intrinsic
) ¼ 20 mMand
K
D
3
intrinsic
(¼K
D
4
intrinsic
) ¼ 5 mMofreactionscheme(2.19). Therefore, identical
equilibrium dissociation constants for each step of a sequential mechanism (like
(2.18)) translate into cooperative binding when intrinsic equilibrium dissociation
constants of accessible sites are computed.
Calculating equilibrium binding curves from any given reaction scheme is quite
straight-forward. One simply writes one equation (2.31) for each molecule of the
reaction
Total concentration ¼ free concentration þ bound concentration (2.31)
This corresponds to (2.24) and (2.25). The bound concentration is the sum of all
molecules bound to all complexes. The set of (2.31) can be solved numerically.
These equations need not be linear, and there may be more than one solution.
A reasonable initial estimate ensures that the right solution is found. This is
discussed in Chap. 5.
2.4 Writing Differential Equations for Two Site Binding
Differential equations can readily be solved with numerical methods, but they have
to be set up first. For example, analyzing reaction scheme (2.18) involves the
calculation of four concentrations, namely [R], [L], [LR], and [L
2
R]. The four
differential equations for the four concentration changes are given in (2.32)–(2.35)
d[R]/dt ¼k
1
[R] [L] þ k
1
[LR] (2.32)
d[L]/dt ¼k
1
[R] [L] þ k
1
[LR] k
2
[LR] [L] þ k
2
½L
2
R] (2.33)
10 2 The Basics
d[LR]/dt ¼ k
1
[R] [L] k
1
[LR] k
2
[LR] [L] þ k
2
½L
2
R] (2.34)
d[L
2
R]/dt ¼ k
2
[LR] [L] k
2
½L
2
R] (2.35)
Note the algebraic signs. Since all concentrations and rate constants are positive,
a decrease in concentration, that is a negative rate, always is indicated by a negative
sign. Note (2.34), where LR is decreased by the dissociation part of reaction 1 and
the association part of reaction 2. Any second order reaction involves three
components of the reactions. Therefore, reaction 1 with k
1
and k
1
affects the
concentration changes of R, L and LR in (2.32 ), (2.33) and (2.34). Likewise,
reaction 2 with k
2
and k
2
involves the components L, LR and L
2
R and thus affects
(2.33), (2.34) and (2.35). For more complex schemes, such a check that a given rate
constant must be involved in three (or two, for reversible first order) reactions helps
in debugging a program. One can use the “find” function included in any text editor
to make sure that each rate constant of a reversible reaction of the second order
appears three times.
Differential equations for reaction scheme (2.19) requi re the calculation of five
concentrations, namely [R], [L], [LR], [RL], and [LRL]. This is shown in equations
(2.36)–(2.40):
d[R]/dt ¼k
1
[R] [L] þ k
1
[LR] k
2
[R] [L] þ k
2
[RL] (2.36)
d[L]/dt ¼k
1
[R] [L] þ k
1
[LR] k
3
[LR] [L] þ k
3
[LR]
k
2
[R] [L] þ k
2
[LR] k
4
[RL] [L] þ k
4
[LRL]
(2.37)
dLR½/dt ¼ k
1
R½L½k
1
LR½k3 LR½L½þk
3
LRL½ (2.38)
d[RL]/dt ¼ k
2
[R] [L] k
2
[RL] k
4
[LR] [L] þ k
4
[LRL] (2.39)
d[LRL]/dt ¼ k
3
[LR][L] k
3
[LRL] þk
4
[LR] [L] k
4
[LRL] (2.40)
The more complex a reaction scheme becomes, the more and longer differential
equations have to be computed. Each reversible reaction corresponds to two
products of rate constant and component of the reactions. Note that the free ligand
L is involved in all four reactions, so that there are eight products in (2.37). There
are two reactions involving the free receptor R in reaction scheme (2.19), so that
there are four products in (2.36). Likewise, two pathways for the dissociation of the
complex LRL are reflected in four products in (2.40).
One important restriction must be considered: Reaction scheme (2.19) contains
a closed loop which corresponds to coupled equilibria calculated in (2.23).
This reduces the number of independent rate constants from 8 (4 reversible
reactions) to 7. Equation (2.23), written for rate constants instead of equilibrium
constants, translates into:
2.4 Writing Differential Equations for Two Site Binding 11
k
1
k
3
k
2
k
4
¼ k
2
k
4
k
1
k
3
(2.41)
Again (2.41) ensures consistency, just like (2.23). It may be interpreted as a rule
for circular reactions: The p roduct of rate constants in one (clockwise) direction of
reaction scheme (2.19) must be the same as the product of rate constants in the other
(counterclockwise) direction. One of the rate constants in a closed loop therefore
can be calculated from the other ones.
2.5 Writing Differential Equations for Any Reaction Scheme
Writing differential equations for a complex reaction scheme may look compli-
cated, but it does not require much fantasy. First, one counts all complexes and free
ligands. Then one has to write one, and possibly a long one, differential equation for
the concentration change of each of these components. For reversible reactions in a
fixed volume in solution, these concentration changes can only be expected from
second or first order reactions. Each second order reaction has to be considered in
the concentration changes of all three components of the reaction. There may be
first order conformational changes which involve only two components (one for
each conformation) or first order decay which only involves one component,
provided the product is irrelevant and the decay is not reversible. Closed circles
in reaction schemes have to fulfill the criterion of (2.41), namely that the products
of all rate constants in one direction must be the same as the products of rate
constants in the other direction.
That is all. But when differential equations are written as part of a progr am code,
no typing error is allowed. It helps to use a “find” function in a program editor and
look for all the rate constants individually. Any rate constant involved in a bimo-
lecular reversible reaction must appear thrice. Whenever a given concentration
appears in the differential equation of this concentration, the algebraic sign in front
of the accompanying rate constant must be negative. For reversible reactions, the
number of products in each differential equation must be even. Those little controls
may help.
2.6 Analytical and Numerical Solutions
Only for the simplest cases, the sets of equations described above can be solved
analytically. But when an analytical solution is found, it is precise and reliable for
all feasible concentrations. Finding analytical solutions needs a lot of effort, but
calculating them can be done from one formula with simple spread sheets or pocket
calculators. Some of the most important analytical solutions are covered in Chap. 3.
12 2 The Basics
Numerical methods are different. They are well established, but they depend on
a computer and a program to run them with. The algorithms are based on
approximations. Th e results are the same within reasonable errors, but they are
not identical to analytical formulas. Figure 5.2 illustrates this with one example. All
calculations done by computers are limited by the precision of the stored variables.
When small differences of large numbers approach the precision of those large
numbers, they become unreliable. Octave and MATLAB typically issue warnings
when the internal precision is not sufficient. In general, whenever stochastic results
are computed with numerical methods, one should repeat the calculations with
other parameters (concentrations or rate constants). Use a computer, but keep
checking it and do not develop unconfined trust!
2.6 Analytical and Numerical Solutions 13
.
Chapter 3
Classical Analytical Solutions
Reversible binding to one site can be calculated with analytical solutions. On the
basis of these formulas, data can be transformed to appear linear. Straight lines of
equilibrium-binding studies in double reciprocal plots or of enzyme kinetics in
Lineweaver-Burk plots or of dissociation kinetics in half logarithmic plots indicate
simple mechanisms. Deviations from these are discussed in detail as cooperative or
independent sites. Logistic funct ions commonly used to calculate dose–response
curves, only correspond to a binding mechanism when the Hill coefficient is one. At
the end of this chapter, the reader should be able to identify simple biochemical
reactions.
3.1 Analytical Solutions for Equilibrium Binding
Simple reversible binding (scheme (2.9)) under equilibrium conditions may be
calculated from (2.15) to (2.17). Computi ng [R] from (2.16) and inserting it into
(2.15) results in the well-known hyperbolic binding function:
[LR] ¼ [L] R0/([L] þ K
D
Þ (3.1)
3.1.1 Direct Binding Curves
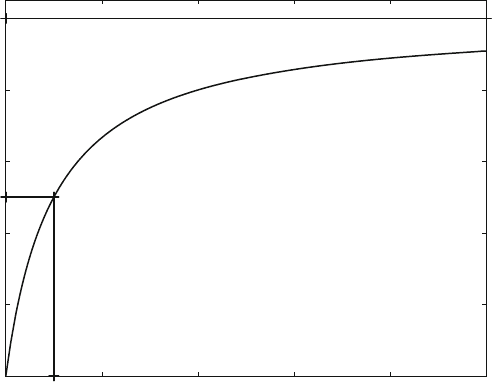
Figure 3.1 shows a binding curve corresponding to (3.1) with a receptor concentra-
tion of 100 mM, a K
D
value of 10 mM and a maximum free ligand concentration of
100 mM. It is characterized by a linear, maximal concentration increase at low free
ligand concentration, followed by a steady decrease in its slope, leading to an
asymptotic approach to its maximal value at high ligand concentrations.
Almost all figures in this textbook show the calculations with Octave programs,
and the names of the program files (like ana1.m) are indicated in brackets after
H. Prinz, Numerical Methods for the Life Scientist,
DOI 10.1007/978-3-642-20820-1_3,
#
Springer-Verlag Berlin Heidelberg 2011
15
the title. The program files are listed as source code and are supplied in the
supplementary material. They are not the topic of Chap. 3, but may serve later as
independent exercises.
The maximal bound ligand is equal to the total receptor concentration R0 ¼ 100
mM, and is indicated as a solid line in Fig. 3.1. The concentration of free ligand
which leads to 50% saturation of receptor (50 mM bound ligand) is equal to the
equilibrium dissociation constant K
D
. This is also indicated as a solid line in
Fig. 3.1.
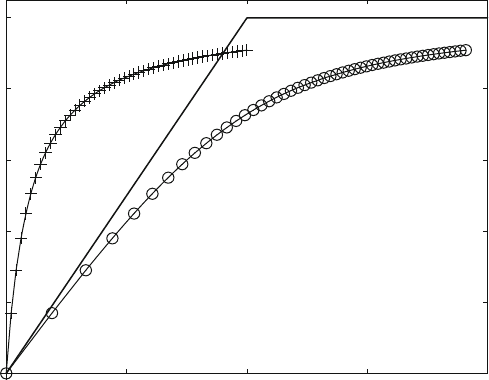
Figure 3.1 shows the calculation with a receptor concentration ten times the
equilibrium dissociation constant. Usually, binding curves are measured with recep-
tor concentrations around the K
D
value. This is not relevant for the shape of the curve
when bound ligand is plotted versus the free ligand concentration (Fig. 3.1 and (+)
in Fig. 3.2). When bound ligand is plotted versus total ligand concentration ((o)
in Fig. 3.2), the curves differ, depending on receptor concentration and affinity. For
extremely high affinities (low K
D
value) or for irreversible reactions, the ligand binds
quantitatively until saturation is reached. This yields a straight line with a sharp bend,
the solid line in Fig. 3.2. The bend marks the total receptor concentration R0.
K
D
values can be determined directly from 50% binding only when binding is
plotted versus the free ligand concentration (Fig . 3.1). When plotted versus total
concentration (Fig. 3.2), the curves may differ considerably, depending on the
receptor conce ntration. In most cases the receptor concentration is in the order of
0
20
40
60
80
100
0 20 40 60 80 100
Concentration of [LR] (bound ligand)
Concentration of [L] (free li
g
and)
Equilibrium Binding curve (ana1.m)
Fig. 3.1 Equilibrium-binding curve (bound ligand vs. free ligand), calculated with R0 ¼ 100 mM
and K
D
¼ 10 mM. The maximal bound ligand R0 and half-maximal bound ligand are indicated by
solid lines, giving the asymptote and the K
D
values, respectively
16 3 Classical Analytical Solutions
magnitude lower than the ligand concentration. For these common cases, bound
ligand is only a tiny fraction of the total ligand concentration so that the difference
between total and free ligand concentration can be disregarded. The concentrations
of pharmacological receptors are much more than thousand times lower than the
administered drugs so that 50% occupation of these receptors is expected when the
total drug concentration (at the target tissue) equals to the K
D
value. If a physiolog-
ical effect is caused only by the binding of a drug to the receptor molecule [1], then
half-maximal b inding to this receptor will lead to a half-maximal effect. The
effective drug concentration for 50% activity (EC
50
) must therefore be equal the
equilibrium dissociation constant K
D
of the drug to the receptor.
3.1.2 Double Reciprocal Plots
If one takes the inverse values of both sides of (3.1), it becomes:
1/[LR] ¼ (1/[L]) ðK
D
/R0Þþ1/R0 (3.2)
0
20
40
60
80
100
0 50 100 150 200
Concentration of [LR] (bound ligand)
Concentration of L0 (o) or [L] (+) (total or free li
g
and)
Equilibrium Binding curve vs. total and free ligand concentration (ana2.m)
Fig. 3.2 Equilibrium-binding curve vs. total and free ligand concentration. R0 ¼ 100 mM,
K
D
¼ 10 mM. Bound ligand [LR] is plotted vs. free (+) and total (o) ligand concentration. Analytical
solutions are calculated with ana2.m. The solid line corresponds to the limiting case of extremely
high affinity or irreversible binding, where all ligands are bound and no free ligand is available until
the receptor is saturated. The sharp bend therefore is observed at L0 ¼ R0 ¼ 100 mM
3.1 Analytical Solutions for Equilibrium Binding 17

Therefore, when 1/[LR] is plotted versus 1/[L], the resulting curve should be a
straight line with a slope of K
D
/R0 and the intersection of 1/R0 at the y-axis. If the
line is extrapolated toward negative values, the intersection with the x-axis will be
at 1/K
D
. This is shown in Fig. 3.3.
Indeed the double reciprocal plot of bound and free ligand (indicated by the
symbol (+)) is linear. Many functions appear linear, or almost linear, in a double
reciprocal plot (compare Figs. 3.4 and 3.5). A double reciprocal plot of bound
ligand versus total ligand ((o) in Fig. 3.2) also appears linear. If this curve would
inadvertently be fitted to a straight line, the resulting K
D
values and receptor
concentrations might be far too high.
3.1.3 Comparison of Scatchard Plots and Double Reciprocal Plots
Double reciprocal plots (Fig. 3.3) sometimes appear linear, even when the plotted
function is not a simple binding curve (o). Another transformat ion of (3.1) is shown
in (3.3)
[LR]/[L] ¼[LR]/K
D
þ R0=K
D
(3.3)
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
-0.1 -0.05 0 0.05 0.1 0.15 0.2 0.25 0.3
1 / [LR] (1/ bound ligand)
1 / [L] (+) or 1 / L0 (o)
Double reciprocal Plot (ana3.m)
Fig. 3.3 Double reciprocal Plot with R0 ¼ 100 mM, K
D
¼ 10 mM (same data as shown in
Fig. 3.2). 1/[LR] is plotted vs. 1/free (+) and 1/total (o) ligand concentration. The theoretical
straight line is extrapolated to (0, 1/K
D
)
18 3 Classical Analytical Solutions
Plotting bound ligand divided by free ligand versus the bound ligand concentra-
tion will give a straight line with a negative slope 1/K
D
. This is called a Scat chard
plot [2–5] and shown in Fig. 3.4. The corresponding double reciprocal plot is shown
in Fig. 3.5.
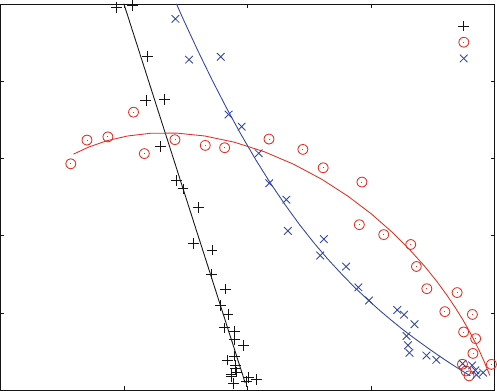
Scatchard plots are more sensitive or responsive than double reciprocal plots.
Higher sensitivity also means that experimental errors influence the shape of the
curve to a larger extent. This becomes obvious when theoretical curves (solid lines
shown in Figs. 3.4 and 3.5) are supplemented with “experimental” data
corresponding to a 5% random noise.
The data points shown in Figs. 3.4 and 3.5 were calculated from ligand
concentrations distributed in a logarithmic scale. Logarithmic distributions help
to get more significant information with the same number of data points. This can
be seen when a double reciprocal plot with linear distribution of data points
(Fig. 3.3) is compare d with the same type of plots and a logarithmic distribution
(Fig. 3.5). Linear distributions plotted in a double recipr ocal scale simply do not
have enough data points at low ligand concentrations. Experimental noise of these
sparsely distributed points influences the shape of the curve disproportionally.
Transformed data such as generated from double reciprocal or Scatchard plots
0
0.01
0.02
0.03
0.04
0.05
0 0.5 1 1.5 2
Bound / Free ligand concentration
Concentration of bound li
g
and
Scatchard Plots (ana4.m)
one binding site
cooperative binding
2 independent sites
Fig. 3.4 Scatchard Plots. R0 ¼ 1 mM. (+) Binding to one site with K
D
¼ 10 mM. (o) cooperative
binding to two equivalent sites (scheme 1.19, K
D
2 ¼ K
D
1), K
D
1 ¼ 100 mM, K
D
3 ¼ 10 mM. (x)
Two independent binding sites [scheme (2.19), K
D
3 ¼ K
D
2] with K
D
1 ¼ 10 mM, K
D
2 ¼ 100 mM.
The theoretical curves plotted are shown as solid lines. A random noise of 5% was assumed for
both free and bound ligand. Data points were calculated from logarithmic distributions of ligand
concentrations
3.1 Analytical Solutions for Equilibrium Binding 19
