Principles of Finance with Excel (Основы финансов c Excel)
Подождите немного. Документ загружается.

PFE Chapter 24: Facts about option prices page 23
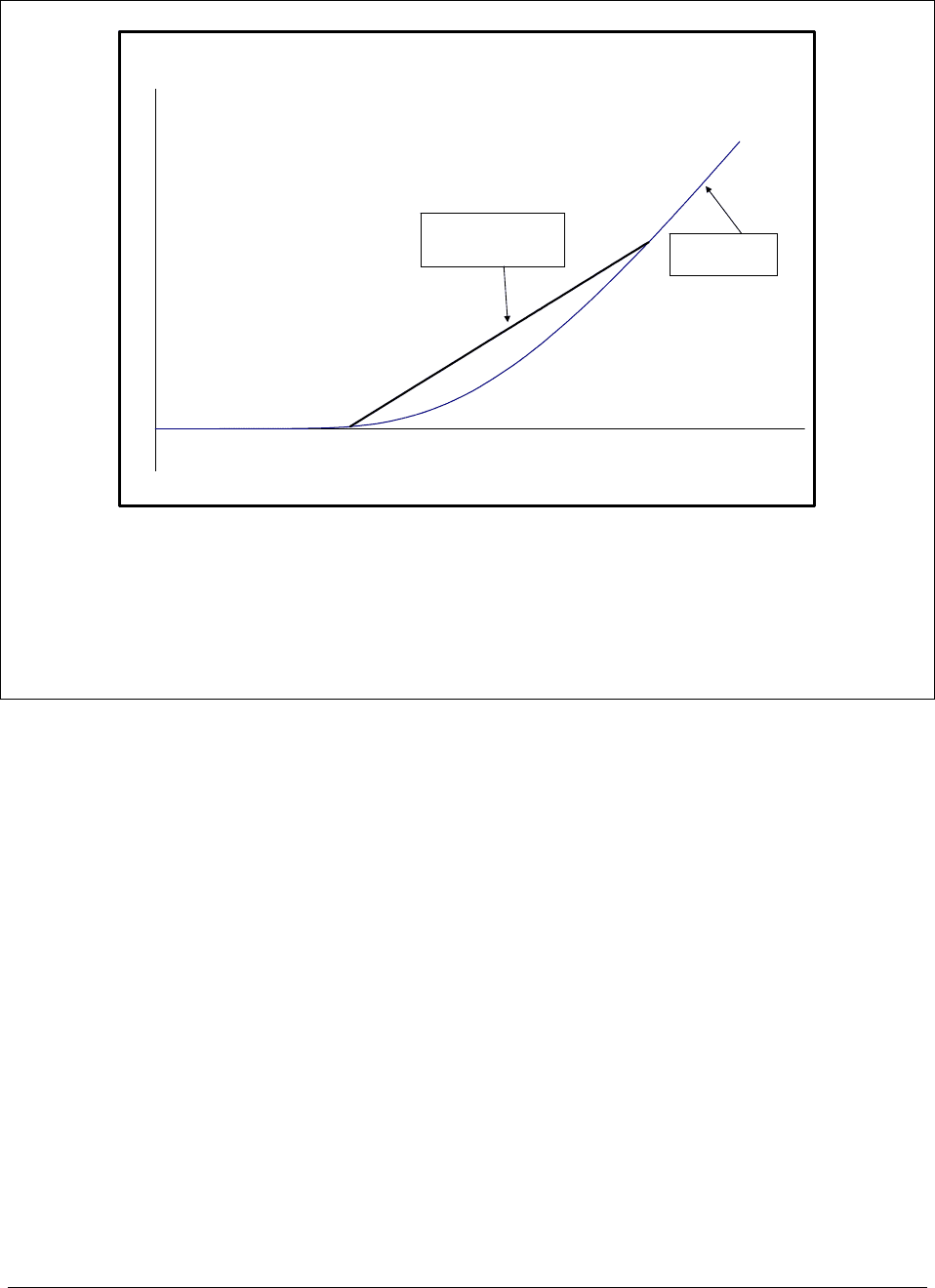
Put Price Convexity
Put exercise price, X
Put price
Put price: Increases
as exercise price
increases
Straight line connecting 2 put
prices: always above
the put pricing line (this is the
convexity)
Figure 24.2: The curved line illustrates the actual put prices for various exercise prices. Put
price convexity means that the line connecting two put prices is always above the actual put
pricing curve.
Summary
In this chapter we have derived restrictions on option prices which stem from their being
related to other securities in the market. These arbitrage restrictions help us bound option prices
(that is, establish minimum prices for put and call options) as well as establish relations between
the prices of various options and the underlying security (as in the case of the put-call parity
theorem).
In this chapter we have dealt with seven such option pricing restrictions, but there are
many more which deal with cases involving dividends and transactions costs. Understanding the

PFE Chapter 24: Facts about option prices page 24
seven restrictions discussed in this chapter will help you understand not only the pricing of
options (we will have more to say on this topic in the next chapter), but it will also help you
understand the way option traders think—they are constantly busy trying to figure out how to
arbitrage option prices.

PFE Chapter 24: Facts about option prices page 25
Exercises
1. You want to buy one American call option contract on Dell Computer Corporation, expiring
in six months, with a strike price of $25. The current stock price is at $24.80. Can the option
price be lower than $0.60? Assume that the interest rate is 8%.
2. Assume that you can buy the above call for $0.50 (which is less than the theoretical
minimum). How can you exploit the mispricing to make a riskless gain?
3. Your generous uncle gives you 10,000 units of the above option as a birthday gift. The stock
price has risen to $28. Will you exercise the option early or rather sell it? Explain.
4. Cash dividends affect option prices through their effect on the underlying stock price.
Because the stock price is expected to drop by the amount of the dividend on the ex-dividend
date, high cash dividends imply lower call premiums. Suppose you own a call option with a
strike price of 90 that expires in one week. The stock is currently trading at $100 and is expected
to pay a $2.00 dividend tomorrow. The call option has a value of $10. What are you going to do:
hold the option or exercise the option early?
5. The Fashion Corporation has stock outstanding that is currently selling for $83 per share.
Both a put and call with a strike price of $80 and an expiration of 6 months are trading. The put
option premium is $2.50, and the risk-free rate is 5 percent. If put-call parity holds, what is the
call option premium?

PFE Chapter 24: Facts about option prices page 26
6. The current market price of a two-month European put option on a non-dividend-paying stock
with strike price of $50 is $4. The stock price is $47 and the risk-free interest rate is 6%.
6.a. If a two-month call option with the same strike price is currently selling for $1, what
opportunities are there for an arbitrageur? How can she exploit arbitrage?
6.b. Would the above market prices still provide an arbitrage opportunity if the stock
would be $46.8/per share in 1 month?
7. In general, what is the problem of using Wall Street Journal prices to search for violations of
the put-call parity relationship?
8. Recall that a Butterfly spread is an options strategy built on four trades at one expiration date
and three different strike prices. For call options, one option each at the high and low strike
prices are bought, and two options at the middle strike price are sold. A Butterfly spread for
ABC stock is created as follows: Sell 1 ABC Jun $180 Call for $20 and buy 2 ABC Jun $200
Call each at $10 and sell 1 ABC Jun $220 Call for $5 (Net premium receive $20-2*$10+$5=5$).
For put options, the trades are reversed: Sell 1 ABC Jun $180 Put, buy 2 ABC Jun $200 Put and
sell 1 ABC Jun $220 Put. Use put-call parity to show that the cost of a butterfly spread created
from the European calls is identical to the cost of the butterfly spread created from European
puts.
9. (Challenge). You have the following information, 25 calendar days before the March 2004
option expiration day:
Strike Put/Call Price

PFE Chapter 24: Facts about option prices page 27
1025 Call $19.8
1025 Put $14.5
1040 Call $12.5
1040 Put $22.17
In the absence of arbitrage, what does the annualized riskfree rate have to be?
10. A European put and a call option both expire in a year and have the same exercise price of
$20. The options are currently traded at the same market price of $3. Assume that the annual
interest rate is 8%. What is the current stock price? In general: If a European put and a call have
the same price and expire at the same time, what can you say about the relationships between the
stock price and the exercise price. S
0
>X? S
0
<X? S
0
=X?
11. You consider buying an American put option on Dell Computer Corporation, expiring in six
months, with a strike price of $25. The current stock price is at $18. What is the minimum price
that you are willing to pay? If you can buy the above put for $5 (which is less than the theoretical
minimum), how can you exploit the mispricing to make a riskless gain?
12. ABC is a non-dividend paying stock. Suppose that S=$17, X=$20, r=5% per annum.
12.a. Can a
European put option that expires in 6 month trade at $2.50? Note that a
European put option may sometimes be worth less than its intrinsic value.
12.b. Consider a situation where the European put option is traded at $2.4. Show how
you can gain from arbitrage.

PFE Chapter 24: Facts about option prices page 28
13. Suppose that you are currently holding an American put option on National Australia Bank
that has an exercise price of $45. The option expires in 6 months. The share price is currently
traded at $23.00.
13.a. Consider a situation where the American put option is traded at $21. Show how
you can gain from arbitrage.
13.b. What is your net payoff if
i.
you exercise the put option today (assume that you invest your proceeds in
bonds with an interest rate of 8%).
ii.
you hold the option until its expiration date.
14. You need to weigh the benefits of early exercise of a put option you hold that expires in 6
month, X=$50, r=20%, with profit you may be giving up by selling the stock today instead of
later. Assume:
14.a. S=$20
14.b. S=$3
In which case you are sure better off exercising the option?
15. Refer to the call options prices given in exercise 8 above. Show that the convexity property
of call prices holds.
16. A butterfly spread is created using the following put options: The investor buys a put option
with a strike price of 55 and pays $15, buys a put with a strike price of 65 and pays $5 and sells
two put with an intermediate strike price of $60.

PFE Chapter 24: Facts about option prices page 29
16.a. What is the upper bound for the X=$60 put price, according to the convexity
property?
16.b. Assume that the X=$60 put price is $12. Draw the profit pattern at maturity for the
butterfly using Excel (let the stock prices at maturity range between $40 and $80). Does
the chart indicate an arbitrage opportunity?
17. At the expiration date the put call parity
000
)()()( SXPVXCallXPut −
+
=
has the
following form
:
TTT
SXXCallXPut
−
+
= )()( or XXPutXCallS
TTT
+
−
=
)()( . Verify this
equation using Excel: Let S
T
range from $20 to $100 and the exercise price X=$60. The option
value at expiry are: Put(X)=Max(S
T
-X,0), Call(X)=Max(X- S
T
,0).
18. Cisco (CSCO) stock sells for $25. The CSCO April 24 call sells for $3 3/8 and the CSCO
April 24 put sells for $1 3/4. The call, put and a Treasury Bill all mature in 4 months. Today’s
price for a Treasury bill which pays off $100 in four months $94.92. Assume that Cisco does not
pay dividends in this period. Use the put-call parity relation to find the arbitrage profit today, if
exists.

PFE Chapter 24, Black-Scholes and binomial page 1
CHAPTER 24: OPTION PRICING—THE BLACK-SCHOLES
FORMULA
*
Current version: September 22, 2002
Chapter contents
Overview......................................................................................................................................... 2
24.1. The Black-Scholes Model..................................................................................................... 4
24.2. What do the Black-Scholes parameters mean? How to calculate them?............................. 5
24.3. Computing
σ
from stock prices ............................................................................................ 7
24.4. Calculating the implied volatility from option prices......................................................... 11
24.5. An Excel Black-Scholes function ....................................................................................... 12
24.6. Doing sensitivity analysis ................................................................................................... 14
24.7. Does the Black-Scholes model work? Applying it to Microsoft options .......................... 16
Summary....................................................................................................................................... 21
Exercises ....................................................................................................................................... 22
*
Notice: This is a preliminary draft of a chapter of Principles of Finance by Simon Benninga
(benninga@wharton.upenn.edu
). Check with the author before distributing this draft (though
you will probably get permission). Make sure the material is updated before distributing it. All
the material is copyright and the rights belong to the author.

PFE Chapter 24, Black-Scholes and binomial page 2
Overview
In the two previous chapters on option pricing, we’ve discussed some facts about options,
but we haven’t discussed how to determine the price of an option. This is the subject of this
chapter.
In this chapter we discuss the Black-Scholes formula. This is the most important option
pricing formula—it’s in wide use in option markets. Everybody “knows” this formula, in the
sense that even non finance people (lawyers, accountants, judges, bankers . . . ) know that
options are priced using Black-Scholes; they may not know how to apply it, and they certainly
wouldn’t know why the formula is correct, but they know that it’s used.
In our discussion of the Black-Scholes model, we’ll make no attempt whatsoever to give
a theoretical background to the model. It’s hopeless, unless you know a lot more math than 99%
of all beginning finance students will ever know.
1
The next chapter discusses the other major technique for solving option prices, the
binomial option pricing model. This model gives some insights into how to price an option, and
it’s also used widely (though not as widely as the Black-Scholes equation). This approach is
somewhat idiosyncratic, since most books discuss the binomial model—which, in a theoretical
sense, underlies the Black-Scholes formula—first and then discuss Black-Scholes. However,
since we have no intention of making the theoretical connection between the binomial model and
Black-Scholes, we’ve chosen to reverse the order and deal with the more important model first.
1
A bitter truth, perhaps. But get this—your professor probably can’t prove the Black-Scholes equation either (don’t
ask him, he’ll be embarrassed). On the other hand—you know how to drive a car but may not know how an internal
combustion engine works, you know how to use a computer but can’t make a central processing unit chip, ....

PFE Chapter 24, Black-Scholes and binomial page 3
What does “pricing an option” mean?
Suppose we’re discussing a call option on Microsoft stock which is sold on 8 February
2002: On this date, Microsoft’s stock price is $60.65. We will look at options on this stock
which have an exercise price of X = $60, and which expire on July 19, 2002. Here’s what
you’ve learned so far:
● From Chapter 21, we know what the terminology means.
● Chapter 21 also tells us what the payoff pattern and profit pattern of the call
option looks like—by itself and in combination with other assets
● Chapter 22 tells us some pricing restrictions on the call option. A simple
restriction (“Fact 1” from Chapter 21) says that
(
)
0
,0Call Max S PV X
>−
. A more
sophisticated restriction (“Fact 3,” put-call parity) says that—once we know the price of
Microsoft stock, the call price, and the interest rate—the put price is determined.
All of these facts are –by themselves—interesting. However, they don’t tell us what the
price of the call option should be. This is the subject of this chapter—the Black-Scholes formula
gives us the an answer—a good one, as you’ll see—to how to price the option.
Finance concepts in this chapter
• Black-Scholes formula
• Put-call parity
• Stock price volatility
• Implied volatility
