Principles of Finance with Excel (Основы финансов c Excel)

Подождите немного. Документ загружается.

PFE Chapter 24: Facts about option prices page 3

Dividends: Throughout the chapter we assume that the stock on which the options are

written does not pay dividends before the option maturity date.

This is not an overly-restrictive

assumption: Stocks which pay dividends tend to do so at regular intervals (quarterly, semi-

annually, or annually). Holders of options on these stocks are thus reasonably sure when the

stocks will pay a dividends. There are thus long periods of time when market participants can be

assured that a stock will not pay a dividend.

For example: General Motors pays a regular quarterly dividend in February, May,

August, and November. An investor who purchases an option on GM in March with an April

maturity knows that in the intervening period no dividends will be paid on the stock.

Many other stocks have never paid a dividend and investors in these stocks’ options can

be reasonably assured that the dividend pricing restriction imposed in this chapter is not

restrictive. Stocks which fall into this category include many of the high-tech stocks whose

options tend to attract the most investor interest.

Finance concepts discussed in this chapter

•

Option pricing restrictions

• No early exercise of calls

• Put-call parity

• Early exercise of American puts

• Option price convexity

The one exception is Section 24.6, where we briefly discuss the effect of dividends.

PFE Chapter 24: Facts about option prices page 4

Excel functions used

• Max

• Sum

• If

24.1. Fact 1: Call price of an option >

(

)

,0Max S PresentValue X−

⎡

⎤

⎣

⎦

It’s 15 August 2001, and you’re considering buying a call option on Microsoft. Currently

the MSFT share itself is selling for

= $63; you want to buy a call on MSFT with an exercise

price

X = $60 and with time to maturity T = 1 year. Furthermore, we’ll suppose that the option

is an

American call option, and can be exercised at any time on or before T.

We will examine Fact 1 in two stages. We start with a “dumb fact,” something that is

obvious once we say it, and then proceed to demonstrate Fact 1 for you.

Dumb fact:

[

]

,0Call price Max S X≥−

Now it’s probably clear to you that the Microsoft option should be selling for at least

$3 $63 $60SX=−= − . To see this, suppose that the option is selling for $2. We’ll devise an

arbitrage strategy—a strategy which will make us money risklessly:

PFE Chapter 24: Facts about option prices page 5

Arbitrage strategy to profit from

call price C = $2 when stock price is S

= $63

and X = $60

Action taken today Cash flow (negative

numbers indicate

costs)

Buy the option -$2

Immediately exercise the option, buying the

stock

-$60

Immediately sell the stock on the open market +$63

Arbitrage profit +$1

So the “dumb fact”—that an American call option should sell for more than the

difference between the stock price and the exercise price—is pretty obvious.

Definition: Arbitrage Strategy

An arbitrage strategy is a combination of assets—usually short or long positions in the

stock, calls and puts on the stock, and a risk-free security—which produces positive cash flows

at all points in time. If you can design an arbitrage strategy for a given set of asset prices (as we

do below), it shows that at least one of the prices is

wrong.

Smart fact:

(

)

,0Call price Max S PV X

⎡

⎤

>−

⎣

⎦

This is a lot less obvious than the previous fact. It’s also a lot more powerful.

The

“dumb fact” above says that the option should sell for at least $3. As the spreadsheet below

shows, the “smart fact” says much more; for example, if the interest rate is 10%, then the smart

fact says that the option should sell for at least $8.45.

How smart? Robert Merton, who first established this and lots of other facts about options, subsequently won the

Nobel Prize for economics, in part for his work on option pricing.

PFE Chapter 24: Facts about option prices page 6

ABC

Microsoft stock price, 15 August 2001, S

Option exercise price, X 60

Option exercise time, T (in years) 1

Interest rate, r 10%

Lower bound on call price

Dumb fact, call price > Max[S

- X,0]

3 <-- =MAX(B2-B3,0)

Fact 1: call price > Max[S

- PV(X),0]

8.45 <-- =MAX(B2-B3/(1+B5)^B4,0)

FACT 1: Lower bound on call price

To prove the “smart fact,” let’s assume that you can buy the call for $5. We’ll show that

there exists an

arbitrage strategy, and we will therefore conclude that the option price is too low.

The arbitrage strategy involves a set of actions at time 0 (today) and at time T (the option

expiration date):

At time 0 (today):

• Short one share of the stock

• Invest in a riskless security paying off the call’s exercise price at time

• Buy a call on the option.

At time T:

•

Purchase the stock on the open market at the time-T price, in order to

close the short position

• Collect from our investment in the riskless security

• Exercise the option if this is profitable

Here’s an example, which assumes that the stock price at time 0 is 63 and that the interest

rate is 10%:

PFE Chapter 24: Facts about option prices page 7

ABC

Microsoft stock price, 15 August 2001, S

Option exercise price, X 60

Option exercise time, T (in years) 1

Interest rate, r 10%

Call price at time 0 (today) 5

Below examine if this price

<-- violates the arbitrage restriction

Actions at time 0 (today)

Short the stock 63 <-- =B2

Buy a bond which pays of X at time T -54.55 <-- =-B3/(1+B5)^B4

Buy a call -5 <-- =-B7

Total cash flow at time 0

3.45 <-- =SUM(B11:B13)

Cash flow at time T

, stock price at time T

Repay the shorted stock -33 <-- =-B17

Collect money from the bond 60 <-- =B3

Exercise the call? 0 <-- =MAX(B17-B3,0)

Total cash flow at time T

27 <-- =SUM(B19:B21)

ARBITRAGE PROOF OF FACT 1

ARBITRAGE STRATEGY

In cells B19:B22 we calculate the cash flow at time

T=1 from the strategy. In the

example above, Microsoft stock at

T is selling for S

= $33. In this case, we would have a

positive time

T cash flow of $27.

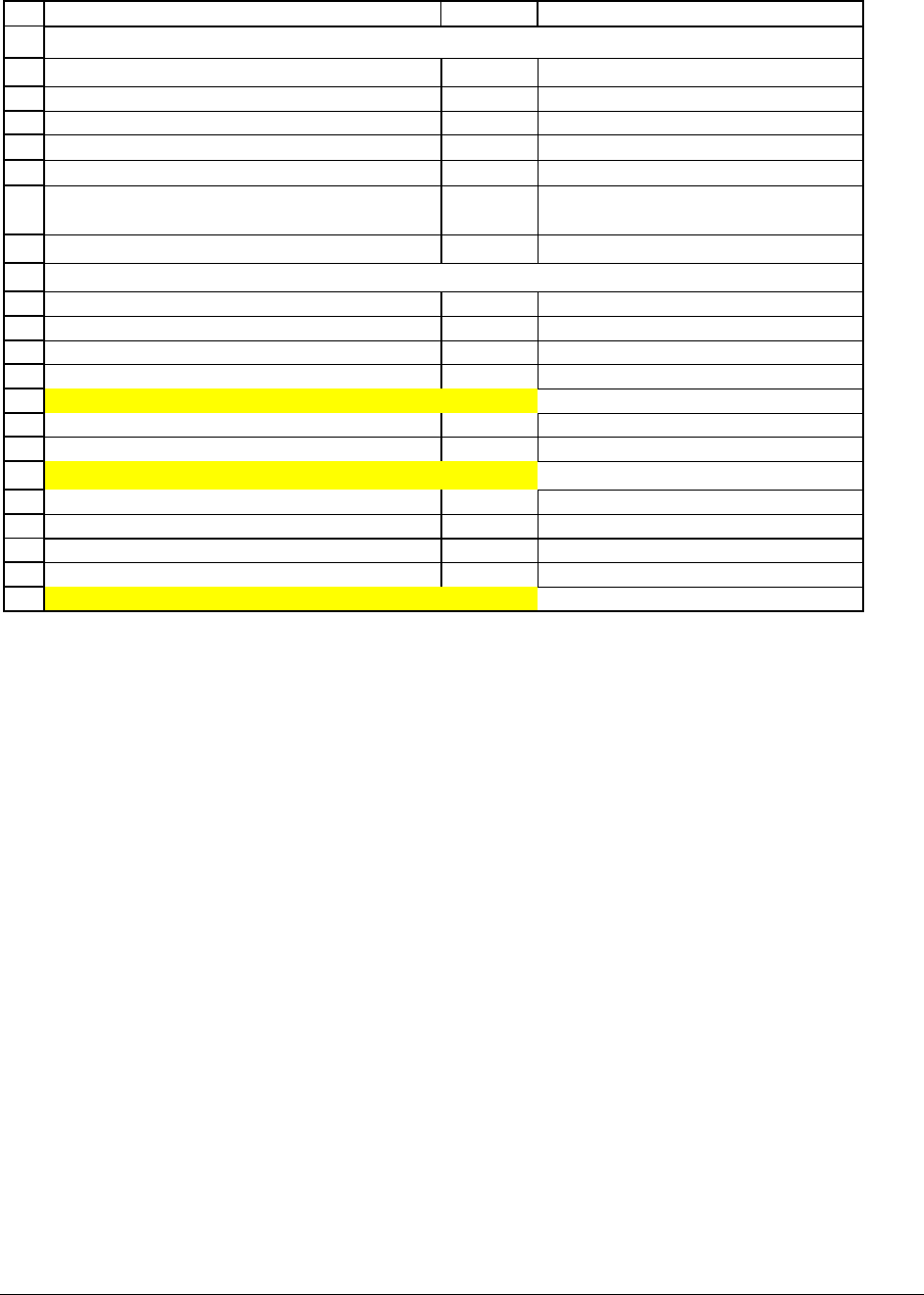
In the example below, we assume that Microsoft stock at

T is S

= $90. In this case you

exercise the call (giving you a positive cash flow of $30), but the total payoff from the strategy is

now $0:

PFE Chapter 24: Facts about option prices page 8

ABC

Microsoft stock price, 15 August 2001, S

Option exercise price, X 60

Option exercise time, T (in years) 1

Interest rate, r 10%

Call price at time 0 (today) 5

Below examine if this price

<-- violates the arbitrage restriction

Actions at time 0 (today)

Short the stock 63 <-- =B2

Buy a bond which pays of X at time T -54.55 <-- =-B3/(1+B5)^B4

Buy a call -5 <-- =-B7

Total cash flow at time 0

3.45 <-- =SUM(B11:B13)

Cash flow at time T

, stock price at time T

Repay the shorted stock -90 <-- =-B17

Collect money from the bond 60 <-- =B3

Exercise the call? 30 <-- =MAX(B17-B3,0)

Total cash flow at time T

0 <-- =SUM(B19:B21)

ARBITRAGE PROOF OF FACT 1

ARBITRAGE STRATEGY

By changing the stock price

, you can see that our strategy always produces no worse

than a zero cash flow at time

T. This makes it an arbitrage strategy:

• At time 0, the cash flow is $3.45 > 0

• At time T, the cash flow is either positive (if the stock price S

< 60) or zero.

You can’t lose from this strategy!! In a rational world this means that something is wrong with

the asset prices. In this case, it’s clear what’s wrong—the call price is too low.

To see this, consider the case where the call price is $10. As you can see below (cell

B14), this means that the initial cash flow from the arbitrage strategy is negative. If the stock

price at time

T is less than $60, say S

= $55, then you will make a future profit (cell B22 below),

but this profit is no longer an arbitrage profit (recall that arbitrage occurs when you can

never

lose money—with a $10 call price, you start off with an initial negative cash flow):

PFE Chapter 24: Facts about option prices page 9

ABC

Call price at time 0 (today) 10

Below examine if this price

<-- violates the arbitrage restriction

Actions at time 0 (today)

Short the stock 63 <-- =B2

Buy a bond which pays of X at time T -54.55 <-- =-B3/(1+B5)^B4

Buy a call -10 <-- =-B7

Total cash flow at time 0

-1.55 <-- =SUM(B11:B13)

Cash flow at time T

, stock price at time T

Repay the shorted stock -55 <-- =-B17

Collect money from the bond 60 <-- =B3

Exercise the call? 0 <-- =MAX(B17-B3,0)

Total cash flow at time T

5 <-- =SUM(B19:B21)

ARBITRAGE STRATEGY

The cash flow at

T (cell B22) is zero, but the initial cash flow (cell B14) is now negative. This

makes more sense:

Negative initial cash flows in this arbitrage strategy start when the call price is > 8.45. If

this is true, then you have to invest money today in order to have a non-negative cash flow in the

future.

We’ve proved our first option pricing fact:

()

,0Call price Max S PV X

⎡

⎤

>−

⎣

⎦

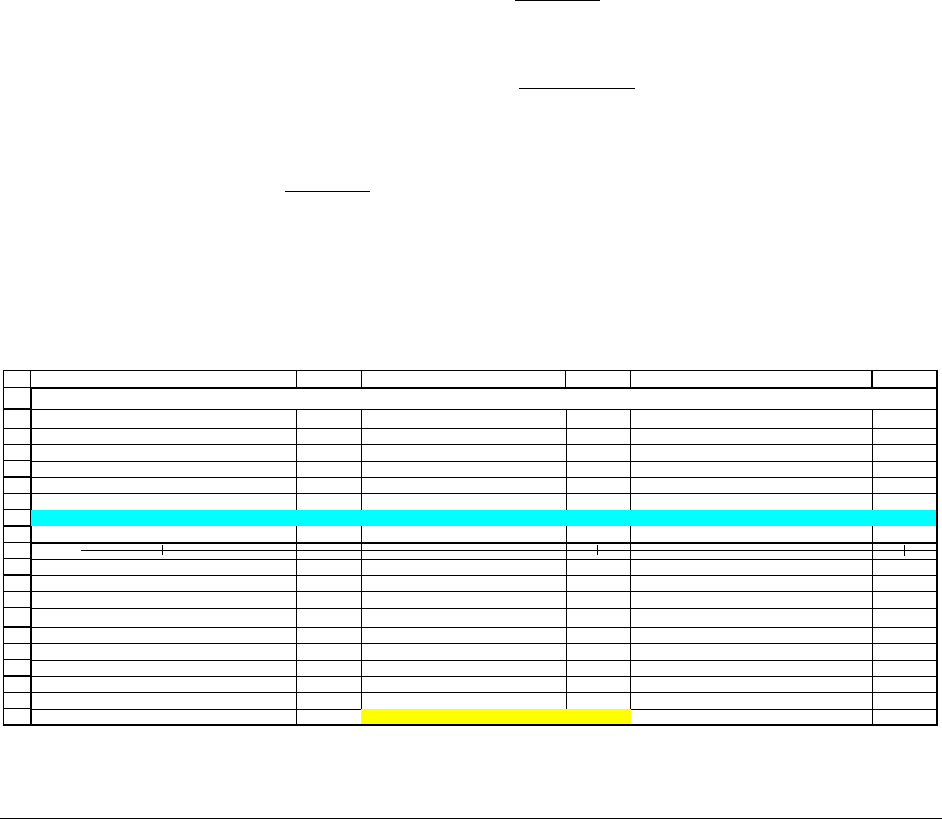
24.2. Fact 2: It’s never worthwhile to exercise a call early.

Suppose that on 15 August 2001 you bought a Microsoft call option for $12 (note that

this price does not violate Fact 1’s price restriction). Furthermore, suppose that the option

expires one year from today, on 15 August 2002.

When the call is written on a non-dividend-paying stock.

PFE Chapter 24: Facts about option prices page 10

Now suppose that after 8 months (approximately 2/3 of a year), you want to get rid of the

option. To make the problem interesting, we’ll assume that the price of Microsoft has risen to

= $80. You have two possibilities:

• You could exercise the option. In this case you would collect $20 =

[

]

[

]

,0 80 60,0

Max S X Max−= −.

• You could also sell the option on the open market. Of course, we don’t know what

the option’s price would be, but Fact 1 tells us that in no case will the price be less

than

()

1/3

,0 ,0

80 ,0 21.876

1 10%

Max S PV X Max S

Max

⎡⎤

−=−⎡⎤

⎢⎥

⎣⎦

⎢⎥

⎣⎦

⎡⎤

=− =

⎢⎥

⎣⎦

The present value

()

1/3

expresses the fact that there is 1/3 of a year left before the

option’s exercise.

What should you do? Clearly you should

sell rather than exercise the call.

ABCDEF

Microsoft stock price, 15 August 2001, S

Option exercise price, X 60

Option exercise time, T (in years) 1

Interest rate, r 10%

Call price at time 0 12

t=0 t=2/3 T=1

Buy option for $12.00 Consider selling the option

or exercising it.

Stock price, S

80.00

Payoff from option exercise 20.00 <-- =MAX(D14-B3,0)

Minimum value of option

according to Fact 1 21.8762 <-- =MAX(D14-B3/(1+$B$5)^(1-2/3),0)

Exercise option or sell it? sell <-- =IF(D18>=D16,"sell","exercise")

FACT 2: No early exercise of calls

Time line

PFE Chapter 24: Facts about option prices page 11

24.3. Fact 3: Put-call parity

(

)

00 0

Put Call PV X S

+−

Put-call parity states that the put price is determined by the call price, the stock price, and

the risk-free rate of interest.

Here’s an example: Suppose that we’re considering a one-year put

option on the Microsoft stock we’ve been discussing throughout this chapter. Recall that

Microsoft stock is currently selling for

= $63. What should be the put price on Microsoft—

where we assume that the put has the same exercise price

X = $60 and the same time to maturity

T = 1?

ABC

Microsoft stock price, 15 August 2001, S

Option exercise price, X 60

Option exercise time, T (in years) 1

Interest rate, r 10%

Call price 15.00

Put price by put-call parity 6.55 <-- =B7+B3/(1+B5)^B4-B2

FACT 3: Put-Call Parit

Another interpretation of put-call parity is that the put price plus the stock price always

equals the call price plus the present value of the exercise price:

(

)

00 0

Put S Call PV X+= + .

This means that given any three of the following four variables—

00 0

,, ,Put S Call X —the fourth

variable is determined.

Again: Recall that the assumption is that the stock pays no dividends before the option maturity date T.

PFE Chapter 24: Facts about option prices page 12

An arbitrage proof of put-call parity (can be skipped on first reading)

We can prove put-call parity by using arbitrage, as specified in the spreadsheet below.

We assume that the stock price is

= $63, the exercise price is X = $60, the time to exercise is T

= 1 year, the interest rate is r = 10%, and the call price is Call

= $15. Given these facts, put-

call parity says that the put price should be

= $6.55 (cell B8).

In cell B11 we suppose that the put price is $3, different from its put-call parity value; we

then show that this makes an arbitrage profitable.

ABC

Microsoft stock price, 15 August 2001, S

Option exercise price, X 60

Option exercise time, T (in years) 1

Interest rate, r 10%

Call price 15

Put price by put-call parity 6.55 <-- =B7+B3/(1+B5)^B4-B2

Arbitrage proof of put-call parit

Put price today (t=0) 3

If this price differs from the

price in cell B8, we will show

that there is a profitable

arbitrage strategy.

Actions at time 0 (today)

Buy stock -63 <-- =-B2

Buy put -3 <-- =-B11

Write call 15

Take a loan of PV(X) at risk-free interest 54.55 <-- =B3/(1+B5)^B4

Total cash flow at time 0

3.55 <-- =SUM(B14:B17)

Cash flow at time T

, stock price at time T

Sell stock 90 <-- =B21

Exercise the put? 0 <-- =MAX(B3-B21,0)

Cash flow from call -30 <-- =-MAX(B21-B3,0)

Repay loan -60 <-- =-B3

Total 0 <-- =SUM(B23:B26)

Arbitrage Proof of Put-Call Parit

Here’s the arbitrage strategy we designed: