Principles of Finance with Excel (Основы финансов c Excel)

Подождите немного. Документ загружается.

PFE Chapter 24, Black-Scholes and binomial page 24

10. Note that you can also calculate the Black-Scholes put option premium as a percentage of

the exercise price in terms of S/X:

() () () ()

()

12 21

ln( / ) 2

rT rT

P SNd XeNd eNd Nd

where

SX r T

dd T

−−

=− − + − ⇒ = − − −

=−

Implement this in a spreadsheet. Find the ratio of S/X for which C/X and P/X cross when T =

0.5, σ = 25%, r = 10%. (You can use a graph or you can use Excel’s Solver.) Note that this

crossing point is affected by the interest rate and the option maturity, but not by σ.

PFE Chapter 25, The Black-Scholes formula page 1

CHAPTER 25: OPTION PRICING—THE BLACK-SCHOLES

FORMULA

Current version: July 18, 2004

Chapter contents

Overview..............................................................................................................................2

25.1. The Black-Scholes Model..........................................................................................4

25.2. What do the Black-Scholes parameters mean? How to calculate them?..................6

25.3. Historical volatility: Computing

from stock prices...............................................7

25.4. Implied volatility: Calculating

from option prices..............................................10

25.5. An Excel Black-Scholes function ............................................................................13

25.6. Doing sensitivity analysis on the Black-Scholes formula .......................................15

25.7. Does the Black-Scholes model work? Applying it to Microsoft options ...............19

25.8. Real options (advanced topic)..................................................................................24

Summary............................................................................................................................29

Exercises ............................................................................................................................30

(benninga@wharton.upenn.edu

PFE Chapter 25, The Black-Scholes formula page 2

Overview

In the two previous chapters on option pricing, we’ve discussed some facts about options,

but we haven’t discussed how to determine the price of an option. In this chapter we show how

to price options using the Black-Scholes formula. The Black-Scholes formula is the most

important option pricing formula. The formula is in wide use in options markets. It has also

achieved a certain degree of notoriety, in the sense that even non finance people (lawyers,

accountants, judges, bankers . . . ) know that options are priced using Black-Scholes. They may

not know how to apply it, and they certainly wouldn’t know why the formula is correct, but they

know that it is used to price options.

In our discussion of the Black-Scholes model, we’ll make no attempt whatsoever to give

a theoretical background to the model. It’s hopeless, unless you know a lot more math than 99%

of all beginning finance students will ever know.

The next chapter discusses the other major model for pricing options, the binomial option

pricing model. The binomial model gives some insights into how to price an option, and it’s also

used widely (though not as widely as the Black-Scholes equation). Most books discuss the

binomial model—which, in a theoretical sense, underlies the Black-Scholes formula—first and

then discuss Black-Scholes. However, since we have no intention of making the theoretical

connection between the binomial model and Black-Scholes, we’ve chosen to reverse the order

and deal with the more important model first.

A bitter truth, perhaps. But get this—your professor probably can’t prove the Black-Scholes equation either (don’t

ask him, he’ll be embarrassed). On the other hand—you know how to drive a car but may not know how an internal

combustion engine works, you know how to use a computer but can’t make a central processing unit chip, ....

PFE Chapter 25, The Black-Scholes formula page 3

What does “pricing an option” mean?

Suppose we’re discussing a call option on Microsoft stock which is sold on 8 February

2002. On this date, Microsoft’s stock price is S

= $60.65. Suppose that the call option has an

exercise price X = $60 and expires on July 19, 2002. Here’s what you’ve learned so far:

• From Chapter 22, you know the basic option terminology. You know what an exercise

price X is, you know the difference between a call and a put, etc. Using Excel you can

also compute the time T to option expiration:

8 2002

19 2002 161

0.4411

2002 365

Days between Feb

and July

Number of days in

===

• From Chapter 22, you also know what the payoff pattern and profit pattern of the call

option looks like—by itself and in combination with other assets

• From Chapter 23, you know that there are some pricing restrictions on the call option. A

simple restriction (“Fact 1” from Chapter 23) says that

()

,0Call Max S PV X

⎡⎤

>−

⎣⎦

. A

more sophisticated restriction (“Fact 3,” put-call parity) says that—once we know the

price of Microsoft stock, the call price, and the interest rate—the put price is determined.

All of these facts are –by themselves—interesting. However, they don’t tell us what the

price of the call option should be. This is the subject of this chapter—the Black-Scholes formula

tells us how what the market price of the option should be.

Finance concepts in this chapter

• Black-Scholes formula

•

Put-call parity

PFE Chapter 25, The Black-Scholes formula page 4

• Stock price volatility

•

Implied volatility

•

Real options

Excel functions used

• Exp

• Ln

• Stdevp

• Varp

• Data Table

25.1. The Black-Scholes Model

In 1973, Fisher Black and Myron Scholes proved a formula for pricing European call and

put options on non-dividend-paying stocks. Their model is probably the most famous model of

modern finance.

The Black-Scholes model uses the following formula to price calls on the

stock:

The 1997 Nobel Prize for Economics was awarded to Myron Scholes and Robert Merton for their role in

developing the option pricing formula. Fisher Black, who died in 1995, would have undoubtedly shared in the prize

had he still been alive.

PFE Chapter 25, The Black-Scholes formula page 5

() ()

()

01 2

ln( / ) 2

CSNd Xe Nd

where

SX r T

dd T

−

=−

Don’t let this formula frighten you! We’re going to show you how to use Excel to

implement the Black-Scholes formula, and you won’t really have to understand the mechanics or

the math (look back at footnote 1 for an explanation). However, if you want some explanations:

C denotes the price of a call, S

is the current price of the underlying stock, X is the exercise

price of the call, T is the call’s time to exercise, r is the interest rate, and

is the standard

deviation of the stock’s return. N( ) denotes a value of the standard normal distribution. It is

assumed that the stock will pay no dividends before date T.

The spreadsheet below prices an option on a stock whose current price is S

=100. The

option’s exercise price is X = 90 and its time to maturity is T = 0.5 (one-half year). The interest

rate is r=4%, and sigma (

, the stock’s volatility—a measure of the stock’s riskiness; more

about this later) is

= 35%.

AB C

S 100 Current stock price

X 90 Exercise price

T 0.50000 Time to maturity of option (in years)

r 4.00% Risk-free rate of interest

Sigma 35% Stock volatility

0.6303 <-- (LN(S/X)+(r+0.5*sigma^2)*T)/(sigma*SQRT(T))

0.3828

<-- d

-sigma*SQRT(T)

N(d

)

0.7357

<-- Uses formula NormSDist(d

)

N(d

)

0.6491

<-- Uses formula NormSDist(d

)

Call price 16.32

<-- S*N(d

)-X*exp(-r*T)*N(d

)

Put price 4.53 <-- call price - S + X*Exp(-r*T): by Put-Call parity

4.53

<-- X*exp(-r*T)*N(-d

) - S*N(-d

): direct formula

The Black-Scholes Option-Pricing Formula

PFE Chapter 25, The Black-Scholes formula page 6

By the put-call parity theorem (see Chapter 23, page000), a put with the same exercise

date T and exercise price X written on the same stock will have price

PCS Xe

−

=− + . We’ve

used this formula in cell B15. Cell B16 includes another version of put pricing—a direct

formula which follows from the Black-Scholes formula.

25.2. What do the Black-Scholes parameters mean? How to calculate them?

The Black-Scholes option pricing model depends on 5 parameters:

•

, the current price of the stock. By this we always mean the stock price on the date

we’re calculating the option price.

•

X, the exercise price of the option (this is also called the strike price).

•

T, the time to the option’s expiration (sometimes called the option maturity). In the

Black-Scholes formula, T is always given in annual terms—meaning: an option with 3

months to expiration has T = 0.25, an option with 51 days until expiration has

0.1397

365

T == ).

•

r, the risk-free interest rate. This is also given in annual terms. Meaning: If the interest

rate is 6% per year and if an option has T = 0.25, then we write r=6% in the Black-

Scholes formula. We usually use the Treasury bill rate for a maturity which is closest to

the option maturity.

•

(“sigma”) is a measure of the riskiness of the stock. Sigma is an important variable in

determining the option price, and it is not a simple concept to explain. We discuss it at

PFE Chapter 25, The Black-Scholes formula page 7

length in Sections 25.3 and 25.4. However, here are some facts to help you get your

bearings on sigma:

o If the stock is riskless, then

= 0% . A stock is riskless if its future price is

completely predictable.

o An “average” U.S. stock has

of between 10% and 25%

o A risky stock may have a

of as much as 80% or 100 %.

25.3. Historical volatility: Computing

from stock prices

There are two main ways to compute the sigma: We can either calculate the sigma by

looking at the series of past stock prices. This computation is sometimes called the historical

sigma or the historical volatility. Alternatively, we can calculate the implied sigma by looking at

options prices; this calculation is often called the implied volatility. This section describes the

computation of the historical volatility, and the next section describes how to compute the

implied volatility.

Below we show the annual prices for Microsoft for the decade from 1991 - 2001.

Column C shows the continuously compounded return for the prices:

continuous

−

⎛⎞

⎜⎟

⎝⎠

Sigma is the standard deviation of these annual returns (cell C18). As you can see, the

computed from these prices is

= 36.90%:

PFE Chapter 25, The Black-Scholes formula page 8

ABC D

Date

Closing

stock

price

Return

31-Dec-90 2.7257

31-Dec-91 5.0104 60.88% <-- =LN(B4/B3)

31-Dec-92 5.4062 7.60%

31-Dec-93 5.3203 -1.60%

31-Dec-94 7.4219 33.29%

31-Dec-95 11.5625 44.33%

31-Dec-96 25.5000 79.09%

31-Dec-97 37.2969 38.02%

31-Dec-98 87.5000 85.27%

31-Dec-99 97.8750 11.21%

31-Dec-00 61.0625 -47.18%

31-Dec-01 66.2500 8.15%

Average return 29.01% <-- =AVERAGE(C4:C14)

Return variance 13.61% <-- =VARP(C4:C14)

Return standard deviation 36.90% <-- =STDEVP(C4:C14)

MICROSOFT STOCK PRICES--ANNUAL DATA

In the world of option pricing it is not usual to compute

from annual data. Most traders

prefer daily, weekly, or monthly data. The use of non-annual data requires some adjustment to

the calculations. We show these adjustments in the example below, where we calculate

Microsoft’s

from monthly data; a discussion of what we did follows the spreadsheet:

PFE Chapter 25, The Black-Scholes formula page 9

ABCD

Date Close

29-Dec-00 43.3750

31-Jan-01 61.0630 34.20% <-- =LN(B4/B3)

28-Feb-01 59.0000 -3.44% <-- =LN(B5/B4)

30-Mar-01 54.6880 -7.59% <-- =LN(B6/B5)

30-Apr-01 67.7500 21.42%

31-May-01 69.1800 2.09%

29-Jun-01 73.0000 5.37%

31-Jul-01 66.1900 -9.79%

31-Aug-01 57.0500 -14.86%

28-Sep-01 51.1700 -10.88%

31-Oct-01 58.1500 12.79%

30-Nov-01 64.2100 9.91%

31-Dec-01 66.2500 3.13%

Monthly return statistics

Average return 3.53% <-- =AVERAGE(C4:C15)

Return variance 1.91% <-- =VARP(C4:C15)

Return standard deviation 13.81% <-- =STDEVP(C4:C15)

Annualized return statistics

Average return 42.36% <-- =12*C18

Return variance 22.88% <-- =12*C19

Return standard deviation 47.84% <-- =SQRT(C24)

MICROSOFT STOCK PRICES

MONTHLY DATA FOR 2001

The standard deviation of the monthly returns is 13.81% (cell C20). The annualized

standard deviation required for the Black-Scholes formula is 47.84% (cell C25). Notice that

since

annual variance = 12* monthly variance

annual standard deviation = 12* monthly variance

12 * monthly standard deviation=

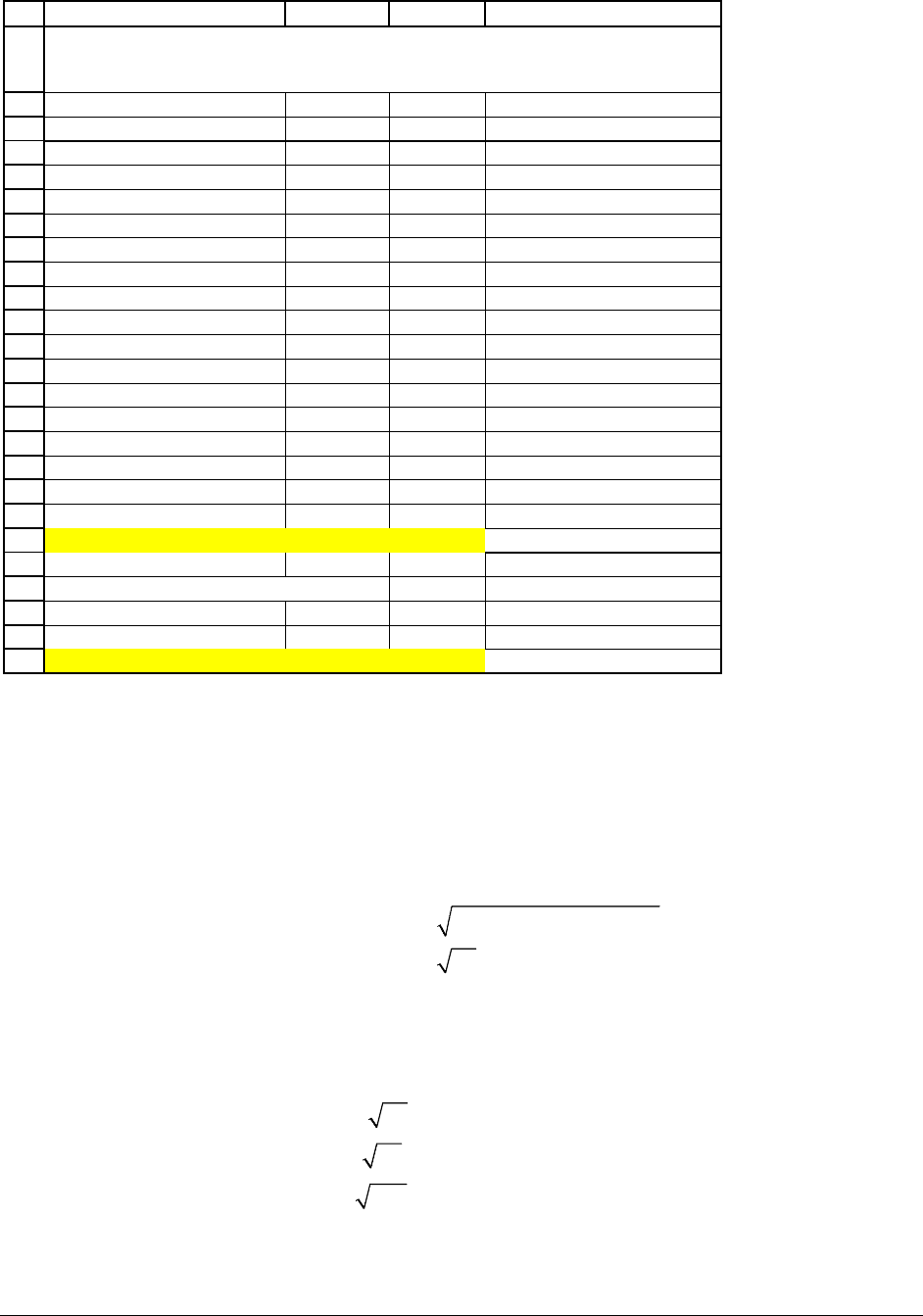
In general, if we’re calculating from non-annual data:

260

annual standard deviation

12 * monthly standard deviation

* weekly standard deviation

* daily standard deviation