Principles of Finance with Excel (Основы финансов c Excel)

Подождите немного. Документ загружается.

PFE Chapter 25, The Black-Scholes formula page 20

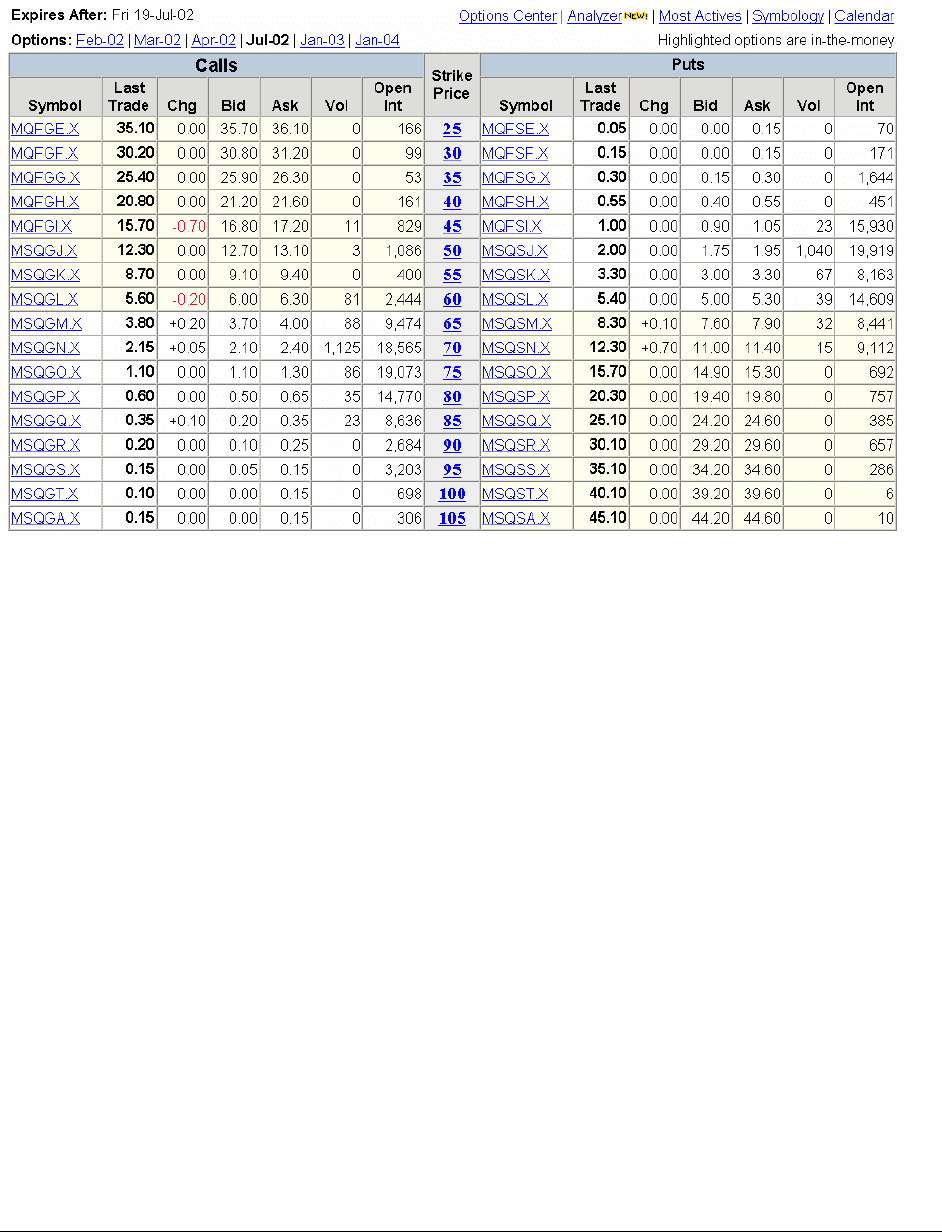
We now look at the closing prices of options on Microsoft stock which expire in July

2002. Clicking on

options in the above box leads us to the option prices:

Look carefully at the above box:

•

Not all the options were traded on 8 February. For example—there was no “volume”

(and hence no trading) of either calls or puts with exercise price (“strike price”) of 25.

•

Significant amounts of call options traded on 8 February were only for exercise prices

X=60, 65, 70, 75, 80, 85. Significant amounts of put options traded were only for

exercise prices X = 45, 50, 55, 60, 65, 70.

•

The price of the “last trade” is in bold face black. But where there is no volume for this

day, the price refers to a previous day’s price.

In the spreadsheet below we look at the Microsoft July call options which actually traded

on 8 February and compare the Black-Scholes price to the actual market price. We use the 6-

month Treasury bill rate of 1.7% as our risk-free rate.

PFE Chapter 25, The Black-Scholes formula page 21

ABC D E F G H

Computing the time to maturity T

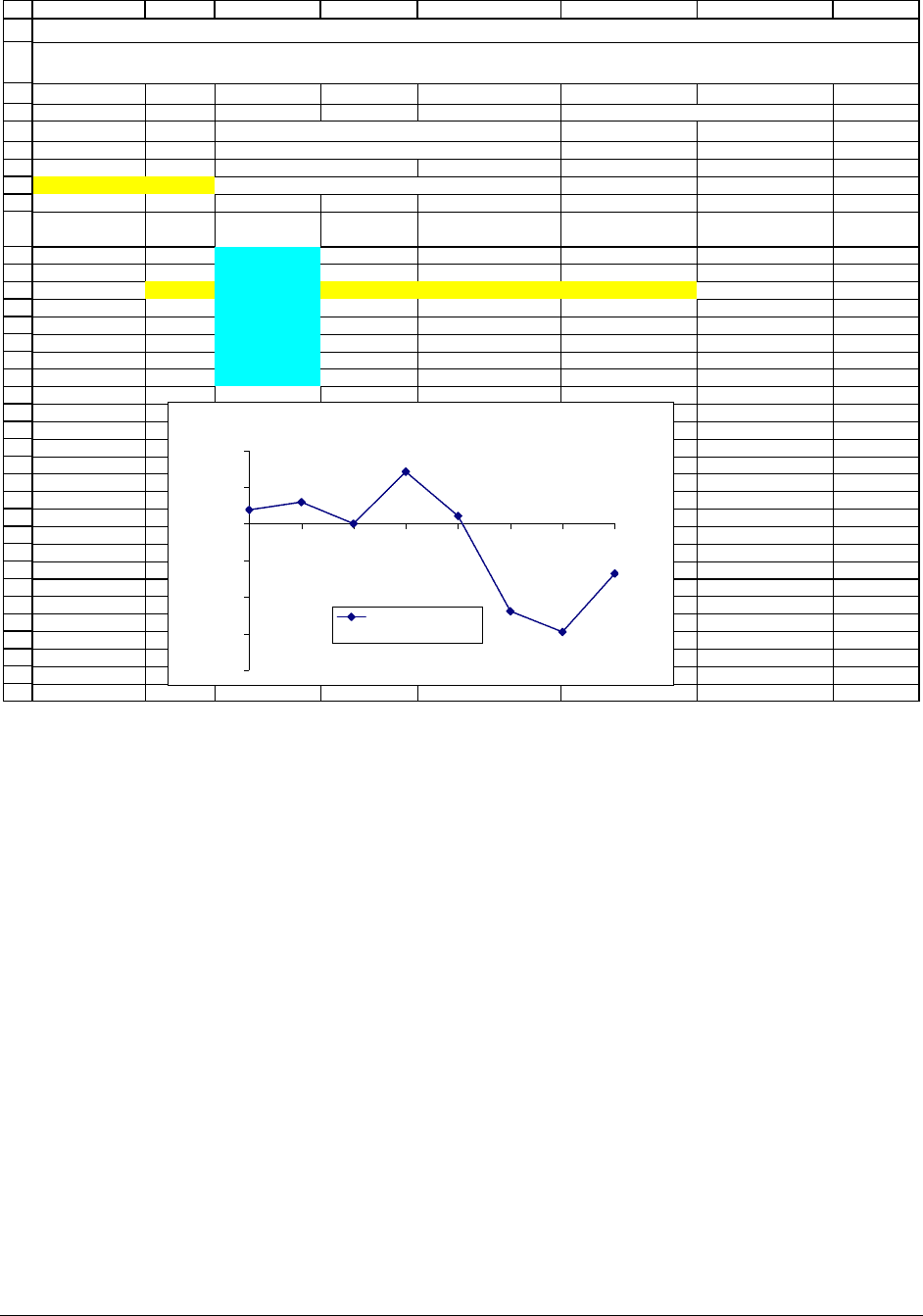
60.65 Microsoft stock, closing price 8 Feb 02 Current date 8-Feb-02

T 0.44110 Time to maturity of option (in years) Expiration date 19-Jul-02

r 1.70% Risk-free rate of interest Time (days) 161 <-- =G6-G5

Sigma 31.66% <-- =CallVolatility(B5,60,B6,B7,D13) Time (% of year) 0.4411 <-- =G7/365

Exercise

price

BS call

price

Actual call

market price

Market minus BS

in dollars

Market minus BS

in percentage

50 12.07 12.30 0.23 1.89% <-- =(D11-C11)/D11

55 8.44 8.70 0.26 2.94% <-- =(D12-C12)/D12

60 5.60 5.60 0.00 0.00%

65 3.53 3.80 0.27 7.08%

70 2.13 2.15 0.02 1.05%

75 1.23 1.10 -0.13 -11.93%

80 0.69 0.60 -0.09 -14.74%

85 0.37 0.35 -0.02 -6.80%

This spreadsheet computes the Black-Scholes value of the Microsoft July 2002 options on 8 February 2002 and compares the prices to the

actual market prices. As you can see, the Black-Scholes formula works pretty well!

MICROSOFT CALL OPTIONS: Comparing BS to actual prices

BS Call Option Pricing

Microsoft July 2002 Call Options

-20%

-15%

-10%

-5%

10%

50 55 60 65 70 75 80 85

Market minus BS

in percentage

We first use the function

CallVolatility to compute the implied volatility of an at-the-

money call (cell B8). We then use this volatility to price all the Microsoft calls using the Black-

Scholes formula (cells C11:C18). Columns E and F compare the Black-Scholes prices to the

actual market prices in cells D11:D18. The Black-Scholes model does a very good job of pricing

the calls.

Below we repeat this exercise for Microsoft July puts.

PFE Chapter 25, The Black-Scholes formula page 22

ABC D E F G H

Computing the time to maturity T

60.65 Microsoft stock, closing price 8 Feb 02 Current date 8-Feb-02

T 0.44110 Time to maturity of option (in years) Expiration date 19-Jul-02

r 1.70% Risk-free rate of interest Time (days) 161 <-- =G6-G5

Sigma 37.35% <-- =putVolatility(B5,60,B6,B7,D14) Time (% of year) 0.4411 <-- =G7/365

Exercise

price

BS put

price

Actual put

market price

Market minus BS

in dollars

Market minus BS

in percentage

45 0.67 1.00 0.33 32.72% <-- =(D11-C11)/D11

50 1.60 2.00 0.40 19.79%

55 3.16 3.30 0.14 4.27%

60 5.40 5.40 0.00 0.00%

65 8.30 8.30 0.00 0.00%

70 11.77 12.30 0.53 4.31%

This spreadsheet computes the Black-Scholes value of the Microsoft July 2002 options on 8 February 2002 and compares the prices to the

actual market prices. As you can see, the Black-Scholes formula works pretty well!

MICROSOFT PUT OPTIONS: Comparing BS to actual prices

BS Put Option Pricing

Microsoft July 2002 Put Options

-5%

10%

15%

20%

25%

30%

35%

45 50 55 60 65 70

Market minus BS

in percentage

The Black-Scholes model works for both puts and calls. The one problematic feature of

the pricing is that the puts are priced at a higher implied volatility than the calls: The implied

volatility of the at-the-money calls is 31.66% versus an implied volatility for at-the-money puts

of 37.35%.

Does the Black-Scholes model work? Looking at implied volatilities

This is our second experiment. We take the Microsoft data above to calculate the implied

volatility for each option (using the functions

CallVolatility and PutVolatility discussed in

Section ????). Here’s our spreadsheet:

PFE Chapter 25, The Black-Scholes formula page 23

ABC D E F G H

Computing the time to maturity

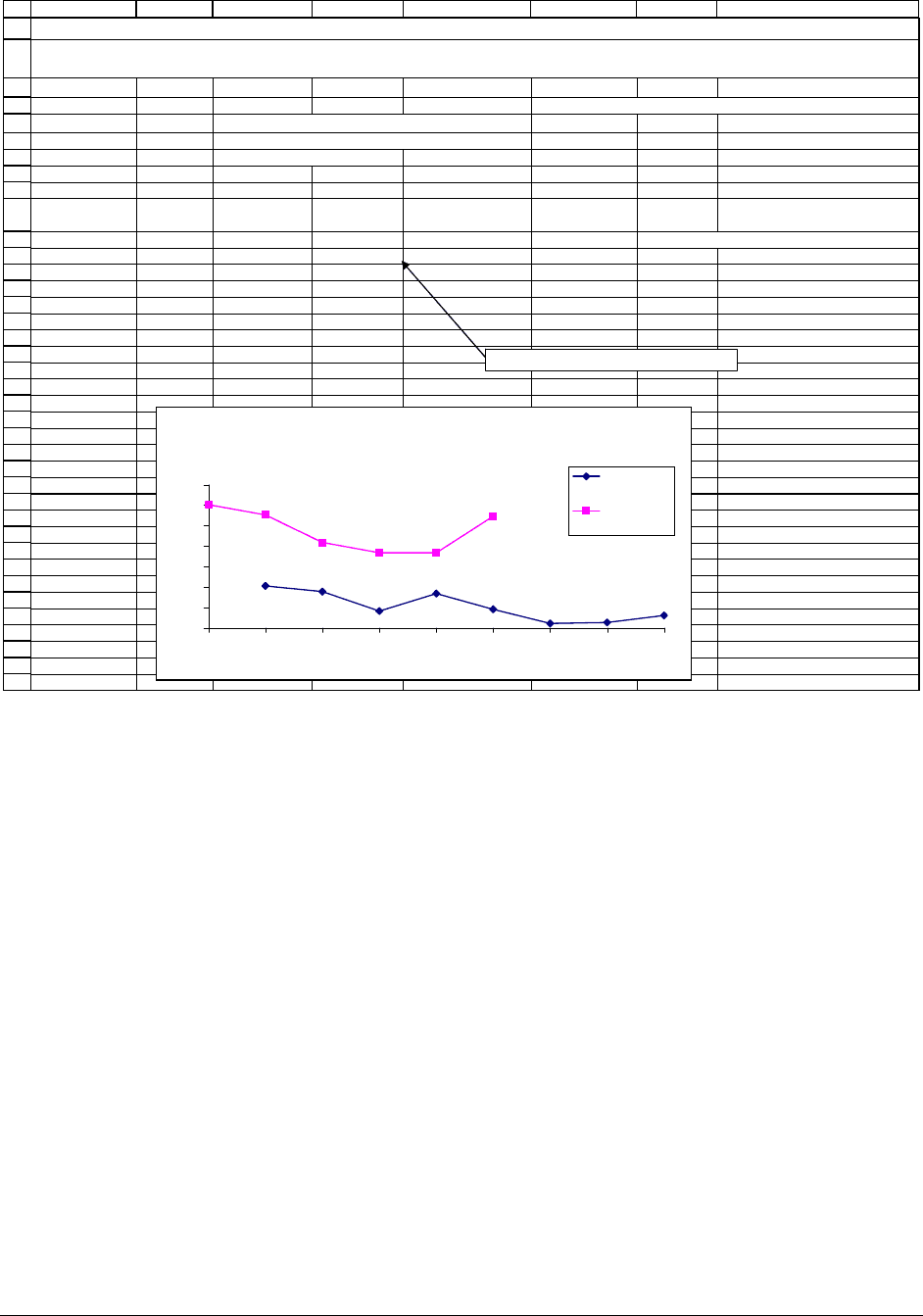
60.65 Microsoft stock, closing price 8 Feb 02 Current date 8-Feb-02

T 0.44110 Time to maturity of option (in years) Expiration date 19-Jul-02

r 1.70% Risk-free rate of interest Time (days) 161 <-- =G6-G5

Time (% of year) 0.4411 <-- =G7/365

Exercise

price

Actual call

market price

Implied call

volatility

ctual put

market price

Implied put

volatility

1.00 42.05% <-- =putVolatility($B$5,B11,$B$6,$B$7,E11)

50 12.30 34.11% 2.00 41.05%

55 8.70 33.56% 3.30 38.37%

60 5.60 31.66% 5.40 37.35%

65 3.80 33.36% 8.30 37.36%

70 2.15 31.82% 12.30 40.92%

75 1.10 30.44%

80 0.60 30.52%

85 0.35 31.22%

This spreadsheet computes the implied volatility of the Microsoft July 2002 options on 8 February 2002. The average implied volatility of the calls is

lower than the average implied volatility of the puts.

MICROSOFT OPTIONS: Computing the implied volatilities

Comparing the Implied Volatility of MSFT July

2002 Calls and Puts

30%

32%

34%

36%

38%

40%

42%

44%

45 50 55 60 65 70 75 80 85

Exercise price, X

Implied call

volatility

Implied put

volatility

=CallVolatility($B$5,B12,$B$6,$B$7,C12)

The results are both encouraging and discouraging:

•

The implied volatilities for the calls are pretty close together, as are the implied

volatilities for the puts. This is good news.

•

On the other hand the implied volatilities for the puts are uniformly larger than the

implied volatilities for the calls. This is strange, since in the Black-Scholes formulation,

the implied volatility refers to the volatility of the stock’s return and hence has nothing to

do with whether we’re discussing a put or a call option.

PFE Chapter 25, The Black-Scholes formula page 24

• On the third hand,

the actual difference between the implied volatilities for the calls and

the puts is not that great (only about 6%).

This is not the place to summarize the vast finance literature on implied volatilities. For

our purposes, the Black-Scholes model works pretty well. That’s enough!

25.8. Real options (advanced topic)

Thus far in this chapter we have discussed the use of the Black-Scholes model to price

call or put options on shares. Such options are sometimes termed financial options because the

option is written on a stock, which is a financial asset. A growing field in finance discusses real

options. A real option is an option which becomes available as the result of an investment

opportunity. Here are some examples of real options:

•

Caulk Shipping is considering the purchase of a license to operate a ferry service from

Philadelphia to Camden. The license requires the company to operate one boat on the

ferry line, but allows Caulk Shipping the possibility of operating as many as ten ferry

boats on the line. This possibility—the option to expand the ferry service—should be

taken into account when Caulk Shipping evaluates the economics of buying the license.

•

Jones Oil is considering the purchase a plot which is known to contain a large quantity of

oil. Tom Shale, the company’s financial analyst has computed the NPV of the lease—he

Harry Truman is reported to have gotten so sick of hearing economists say “On the hand, ... . But on the other

hand, ... ” that he asked his chief of staff to get him a “one-handed economist.” History does not record if he

succeeded. The economist in this section’s bullets has at least 3 hands. Harry Truman would not have liked him.

PFE Chapter 25, The Black-Scholes formula page 25

assumes that once the oil drilling equipment is in place, the company will pump the oil

out of the ground at the maximum feasible rate. However, Tom also realizes that the

financial analysis of the plot purchase should include an important real option: If the

future oil price is low, Jones Oil can stop pumping the oil and wait until the price gets

higher. This option to delay has obvious value.

•

Merrill Widgets is considering the purchase of six new widget machines to replace

machines which are currently in place. The new machines employ an innovative

production technology and are much more sophisticated than the old machines. Simona

Mba, the company’s financial analyst, has determined that the NPV of replacing a single

machine is negative, and thus recommends against the replacement. Roberta Merrill, the

company’s owner, has a slightly different logic: She wants to purchase one widget

machine in order to learn about the machine’s possibilities; after a year she will then

decide whether to buy the remaining five widget machines. The purchase of a single new

widget machine gives Merrill Widgets the option to learn. The company’s financial

analysis should value this option. Below we return to this case and show how to value

the option to learn.

A simple example of the option to learn

In the rest of this section we will show how the Black-Scholes model can be used to

value Merrill Widget’s option to learn. Recall that the company is considering replacing each of

its existing six widget machines with a new machines. The new machines cost $1,000 each and

have a five-year life. Simona Mba, the company’s financial analyst, has estimated the expected

per-machine cash flows; these flows are defined as the incremental cash flow of replacing a

PFE Chapter 25, The Black-Scholes formula page 26

single old machine by a new machine and include the after-tax savings from introducing new

machines, the tax shield on incremental depreciation from replacing an old by a new machine,

and the sale of the old machine. It is important to emphasize that management does not know

the exact realization of these annual cash flows, but knows only their expected values. The

expected cash flows for the new machine are given below.

ABCDEFG

Year 012345

CF of sin

le machine -1000 220 300 400 200 150

Simona estimates the risk-adjusted cost of capital for the project as 12%. Using the expected

cash flows and a cost of capital of 12% for the project; Simona has concluded that the

replacement of a single old machine by a new machine is unprofitable, since the NPV is

negative:

()()()()

48.67

12.1

150

12.1

200

12.1

400

12.1

300

12.1

220

1000

5432

−=+++++−

Now comes the (real options) twist. Roberta Merrill, the company’s owner, says: “I

want to try one of the new machines for a year and learn the true realization of its cash flows. At

the end of the year, if the experiment is successful, I want to replace five other similar machines

on the line with the new machines. If I do not try one of the new machines, I will never know

their true cash flows.”

Does this change our previously negative conclusion about replacing a single machine?

The answer is “yes.” To see this, we now realize that what we have is a package:

•

Replacing a single machine today. This has a NPV of –67.48.

•

The option of replacing 5 more machines in one year. We can view each such option

as a call option on an asset which has current value of:

PFE Chapter 25, The Black-Scholes formula page 27

()()()()

52.932

12.1

150

12.1

200

12.1

400

12.1

300

12.1

220

5432

=++++=S

and an exercise price X = 1,000. Of course these call options can be exercised only if

we purchase the first machine now; in effect the real options model will be pricing the

learning costs.

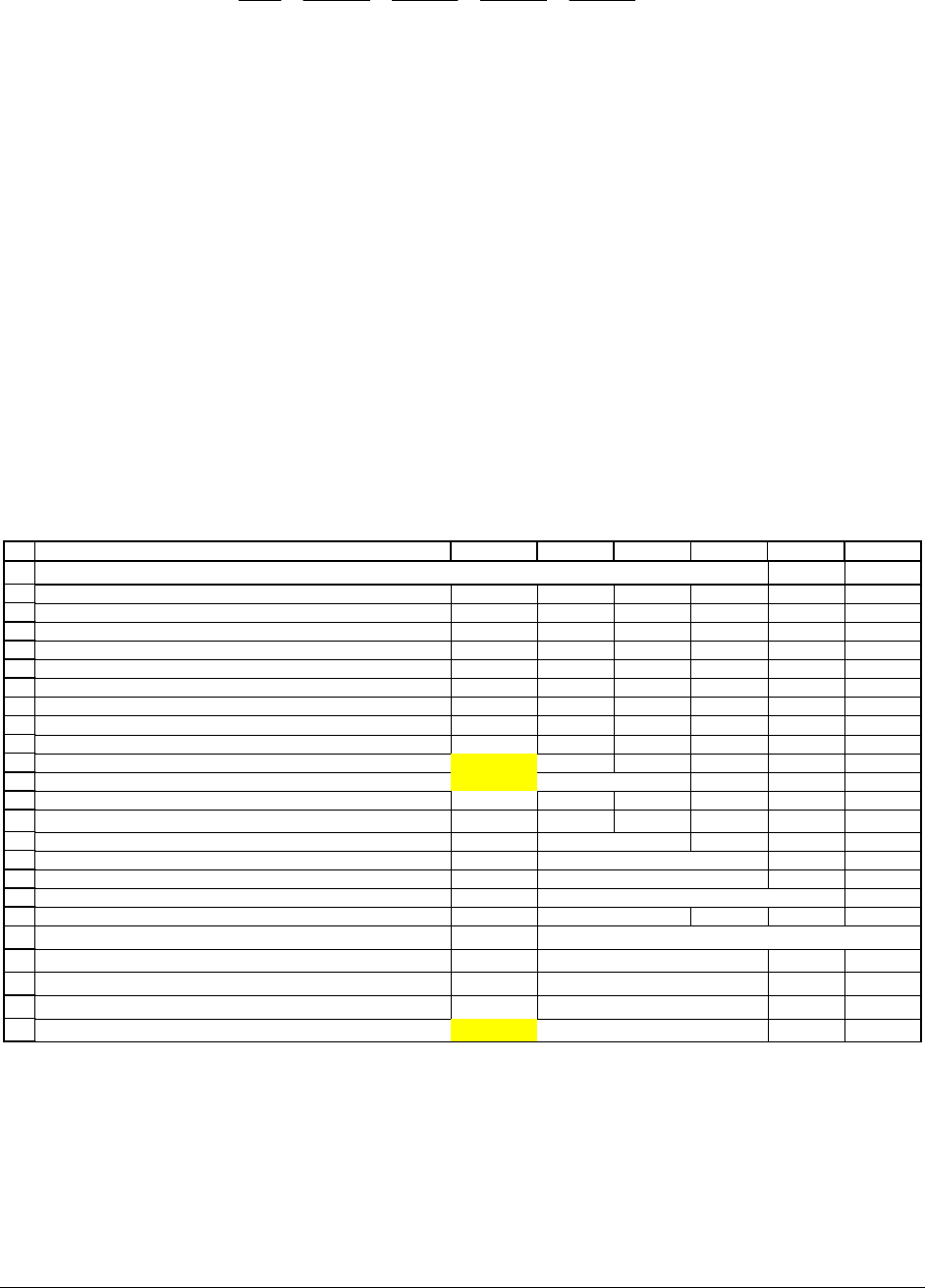
Let’s suppose that the Black-Scholes option pricing model can price this call option. We

further suppose that the risk-free rate is 6% and the standard deviation of the cash flows is

40%. The next figure shows that the value of the each of the options to acquire one machine in

one year is $143.98. It now follows that the value of the whole project is $652.39 (cell B12):

67.48 5*143.98 652.39

Project value = NPV of first machine+ 5 options to acquire

=− + =

ABCDEFG

Year 0 12345

CF of single machine -1000 220 300 400 200 150

Discount rate for machine cash flows 12%

Riskless discount rate 6%

NPV of single machine -67.48

Number of machines bought next year 5

Option value of single machine purchased in one more year 143.98 <-- =B24

NPV of total project 652.39 <-- =B8+B10*B11

Black-Scholes Option Pricing Formula

S 932.52 PV of machine CFs

X 1000.00 Exercise price = Machine cost

r 6.00% Risk-free rate of interest

T 1 Time to maturity of option (in years)

Sigma 40% <-- Volatility

0.1753 <-- (LN(S/X)+(r+0.5*sigma^2)*T)/(sigma*SQRT(T))

-0.2247

<-- d

- sigma*SQRT(T)

N(d

)

0.5696

<--- Uses formula NormSDist(d

)

N(d

)

0.4111

<--- Uses formula NormSDist(d

)

Option value = BS call price 143.98

<-- S*N(d

)-X*exp(-r*T)*N(d

)

THE OPTION TO EXPAND

Thus, buying one machine today, and in the process acquiring the option to purchase five more

machines in one year is a worthwhile project.

PFE Chapter 25, The Black-Scholes formula page 28

One critical element here is the volatility. The lower the volatility (i.e., the lower the

uncertainty), the less worthwhile this project is. By building a data table we can examine the

relation between the standard deviation

and the project value:

BCDEFGHIJ

652.39 <-- Table header: =B12

1% -63.48

10% 97.16

20% 283.09

30% 468.40

40% 652.39

50% 834.59

60% 1014.54

70% 1191.81

Data Table

Project Value as Function of Sigma

-200

200

400

600

800

1000

1200

1400

0% 10% 20% 30% 40% 50% 60% 70% 80%

Sigma

The value of the project as a whole comes from our uncertainty about the actual cash

flows one year from now. The less is this uncertainty (measured by

), the less valuable the

project. In this particular example a very low uncertainty (

> 4.75%) with respect the machine

cash flow returns is sufficient to justify its purchase.

Estimating the

for real option cash flows is problematic, since there is little market data (as there is for stocks) to

guide us. Many authors use estimates in the range of 30% - 50% for the standard deviation of real option returns;

this is somewhat higher than the average standard deviation of U.S. market returns for equity, which are in the range

of 15% - 30%. To explore this issue, consult one of the three leading books in the area: Lenos Trigeorgis, Real

Options: Managerial Flexibility and Strategy in Resource Allocation, MIT Press, 1996; Martha Amram and Nalin

Kulik, Real Options, Harvard Business School, 1998; Tom Copeland and Vladimir Antikarov, Real Options: A

Practitioner’s Guide, Texere, 2001.

PFE Chapter 25, The Black-Scholes formula page 29

Real options: where do we go from here?

Real options are increasingly used in finance to value corporate investments. The

example of Merrill Widgets given above is only a small example of the use of the real options

technique. For deeper discussions, we suggest you consult one of the books mentioned in

footnote 000.

Summary

This chapter has given you a quick and hopefully practical insight into how to use the

Black-Scholes model. The Black-Scholes model is remarkably good at pricing options and is

widely used. It is also easy to use, provided you don’t get too hung up on the details of where

the formula comes from (in this chapter we’ve left these hang-ups behind us, and concentrated

exclusively on implementational details).