Презентация - Андреев В.К. Механика жидкости и газа
Подождите немного. Документ загружается.

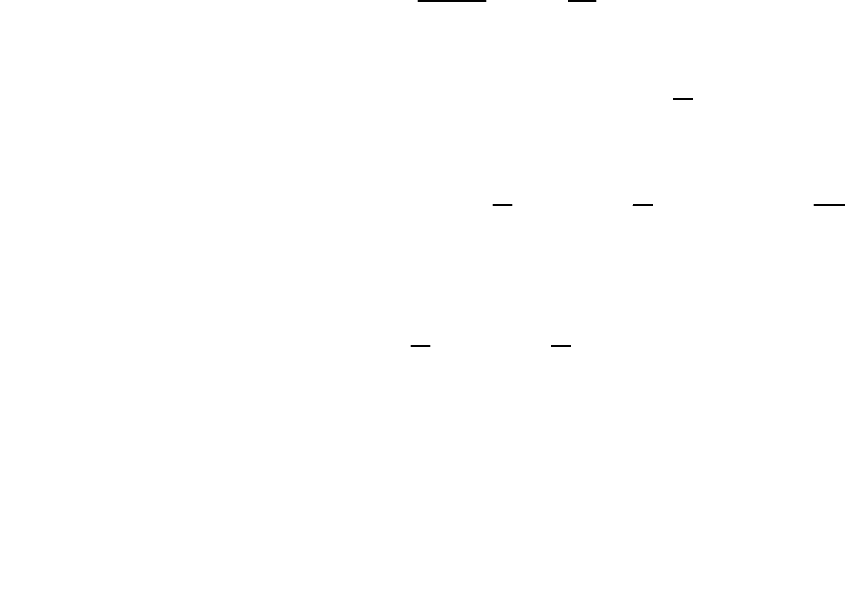
00
[1()]
Ж
pp
ρρβ=+−,
00
()
C
mmpp
β=+−,
и вычислим произведение
m
ρ
перемножив (27.10) на (27.1 1):
2
00000000
()()()
ЖCcЖ
mmmpppp
ρρρβρβρββ=++−+−
.
Последним слагаемым в правой части полученного выражения ввиду его ма
лости по сравнению с
двумя другими слагаемыми можно пренебречь (напомним, что для нефти
ж
β
изменяется в диапа
зоне от
10
710
−
⋅
Па
-1
до
10
3010
−
⋅
Па
-1
, а для пластовых вод диапазон изменения лежит в пределах от
10
2,710
−
⋅ Па
-
1
до
10
510
−
⋅
Па
-1
и что коэффициент объемной упругости пласта составляет:
10
(0,32)10
с
β
−
=−⋅
Па
-1
).
Тогда, с учетом (27.5), получим:
*
0000
[1()/]
mmppm
ρρβ=+− ,
откуда после дифференцирования выражения по времени t находим:
*
0
()
mp
tt
ρ
ρβ
∂∂
=
∂∂
. (27.13)
Теперь преобразуем правую часть равенства
()
k
dp
ρ
µ
∆
∫
.
Подставив под знак интеграла уравнение состояния упругой жидкости (27.10), получим
2
000
()(())
2
Ж
kkp
dppppC
ρρρβ
µµ
∆=∆+−+
∫
,
но снова учитывая, что жидкость слабосжимаемая и коэффициент
ж
β
мал, пренебрежем вторым
слагаемым и в результате получим
0
()
kk
dpp
ρρ
µµ
∆=∆
∫
. (27.15)
Подставив (27.13) и (27.15) в исходное дифференциальное уравнение (27
.12), получим
дифференциальное уравнение относительно давления:
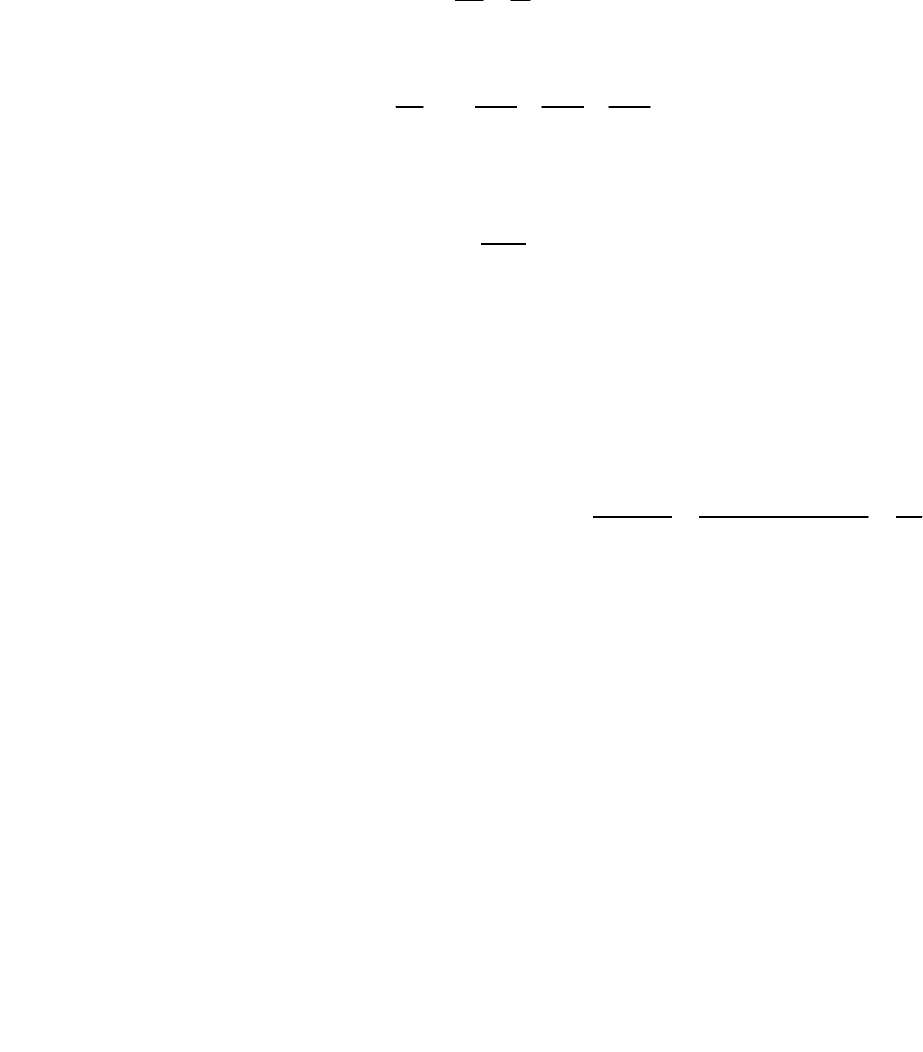
*
pk
p
t
β
µ
∂
=∆
∂
(27.16)
или, в декартовой системе координат
222
222
()
pppp
t
xyz
κ
∂∂∂∂
=++
∂ ∂∂∂
, (27.17)
где введено обозначение
*
k
κ
µβ
= . (27.18)
Уравнение (27.16) - основное дифференциальное уравнение теории упругого режима фильтрации.
Коэффициент k , характеризующий скорость перераспределения пласто
вого давления при
неустановившейся фильтрации упругой жидкости в упругой п
ористой среде, В.Н.Щелкачев назвал
коэффициентом пьезопроводности пласта по аналогии с
коэффициентом температуропроводности в
уравнении теплопроводности.
Размерность коэффициента пьезопроводности к можно установить из (27.18):
22
*1112
[]
[][]
kLL
T
LMTLMT
κ
µβ
−−−
===,
где L, М, Т -
соответственно размерности длины, массы и времени. Наиболее часто встречающиеся в
нефтепромысловой практике значения коэффициента пьезопроводности заключены в пре
делах от 0,1 до
5 м
2
/с.
Лекция 32
§28. Теория двухфазной фильтрации
Практическая важность изучения двухфазных течений в пористых ср
едах.
Рассмотрим здесь наиболее простое двухфазное течение, соответст
вующее вытеснению жидкости,
первоначально заполнявшей поры, другой жидкостью, не смешивающейся с первой.
В случае
одномерного течения несжимаемых несмешивающихся жидкостей в условиях, когда поверхност
ное
натяжение между фазами невелико и можно пренебречь капиллярным давлением, а также вли
янием
силы тяжесчи. процесс вытеснения допускает простое математическое описание, впе
рвые предложенное
американскими исследователями С. Бакли и М. Левереттом (1942г.).

Это описание основано на введении понятия насыщенности, относительных фазовых
проницаемостей и использовании обобщенного закона Дарси.
Физические представления и математическое описание процесса вытеснения одной жидкости другой.
Рассмотрим процесс вытеснения, происходящий в прямолинейном тонком горизонтальном
образце, представленном однородной и изотропной пористой средой, т. е. его пористость m
и
проницаемость k постоянны. Координата x отсчитывается вдоль образца, направление течения -
горизонтальное. Поперечное сечение образца (площадь сечения обозначим
ω
) предположим
достаточно малым, так что давление и насыщенность можно считать постоянными п
о сечениям.
Давление р в водяной и нефтяной фазах считаем одинаковым в силу пренебре
жения капиллярным
давлением, обе фазы несжимаемы, температура постоянна.
В рассматриваемый образец, первоначально заполненный нефтью, через сечение x = 0
закачивается вода
. В процессе выгеснения образуется зона совместного движения воды и нефти. При
совместном течении двух фаз в пористой среде по крайней мере одна из них образует связную систему,
граничащую со скелетом породы и частично с другой жидкостью. Из-за избирательного
смачивания
твердой породы водой площадь контакта каж
дой из фаз со скелетом пористой среды значительно
превышает площадь контакта фаз между собой. Это позволяет счи
тать, что основной вклад в
сопротивление движению дает взаимодействие каждого флюида с твердым скеле
том пласта, и в первом
приближении пренебречь эффектом увлечения одной жидкостью другой. При этом, естествен
но,
сопротивление, испытываемое каждой фазой при совместной фильт
рации, отлично от того, которое
было бы при течении только одной из них. З
акон фильтрации каждой фазы можно представить в виде
обобщенного закона Дарси в дифференциальной форме:
()
вв
в
в
Qksp
wk
x
ωη
∂
==−
∂
; (28.1)
()
нн
н
н
Qksp
wk
x
ωη
∂
==−
∂
.
Здесь
,
вв
wQ
и
,
нн
wQ
- скорости фильтрации и объемные расходы соответственно воды и нефти;
,
вн
ηη
-
коэффициенты динамической вязкости фаз;
(),()
вн
ksks
- относительные фазовые проницаемости:
в
ss
≡
- водонасыщенность.

Для рассматриваемого двухфазного течения водо- и нефтенасы-щенность
н
s
связаны очевидным
соотношением
1
вн
ss
+=
. (28.2)
Для вывода уравнения неразрывности рассмотрим баланс каждой фазы как однородной жидкости
,
примененный к фиксированному элементарному макрообъему
Vx
ω
∆=∆
, содержащему
обе фазы. Если
за некоторый промежуток времени
t
∆
в объем
V
∆
втекает большее
количество жидкости, чем
вытекает, то она должна накап
ливаться в этом объеме, и ее насыщенность увеличивается (и наоборот).
Исходя из этого и сформулируем закон сохранения массы каждой фазы.
Так, для воды изменение массы находим в направлении течения по оси x,
помня, что ее плотность
в
ρ
постоянна в силу предположения о несжимаемости. Через сечение с координатой x
за промежуток
t
∆
втекает в объем
V
∆
масса воды
(,)
вв
wxtt
ρω
∆
, а вытекает через сечение
xx
+∆
масса, рав
ная
(,)
вв
wxxtt
ρω
+∆∆
, так что изменение массы воды в объеме
V
∆
за время
t
∆
равно:
[(,)(,)]
ввв
V
wxtwxxtt
x
ρ
∆
−+∆∆
∆
,
где
/
Vx
ω
∆∆=
.
С другой стороны, это изменение массы должно быть сбалансировано
за счет изменения во
времени водонасышенности в поровом объеме
mV
∆
:
[(,)(,)]
в
msxttsxtV
ρ
+∆−∆
.
Приравняв два последних выражения, разделив обе части полученного равенства на
в
Vt
ρ
∆∆
и
перейдя к пределу при
0,0
xt
∆→∆→
, получим:
или 0
вв
wssw
mm
xttx
∂∂∂∂
−=+=
∂∂∂∂
. (28.3)
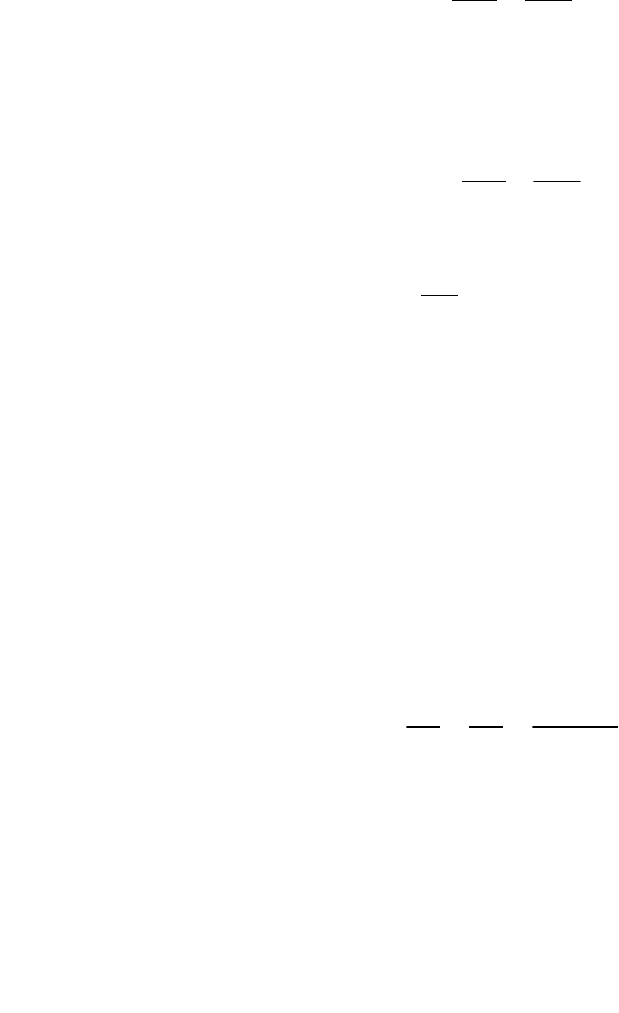
Аналогично выводится уравнение сохранения массы нефти:
0
нн
sw
m
tx
∂∂
+=
∂∂
, (28.4)
которое в силу (28.2) можно представить в виде
0
н
sw
m
tx
∂∂
−+=
∂∂
. (28.5)
Сложив уравнения неразрывности (28.3) и (28.5) для обеих фаз, получим:
()0
вн
ww
x
∂
+=
∂
,
(28.6)
откуда найдем первый интеграл:
()
или ()
внвн
wwwtQQQt
+=+=
. (28.7)
Равенства (28.6) или (2
8.7) показывают, что суммарная скорость и двухфазного потока (а значит, и
суммарный расход фаз Q(t) не зависит от координаты x, т.е. является либо постоянной вели
чиной, либо
известной функцией времени. Это - следствие предположения о несжимаемости фаз.
Уравнения (28.1), (28.3). (28.5) или (2
8,7) полностью описывают процесс вытеснения и позволяют
определить неизвестные функции
(,)
sxt
,
(,)
в
wxt
,
(,)
н
wxt
,
(,)
pxt
.
Покажем, что. исключив другие
зависимые переменные, можно вывести уравнение, которое содержит только водонасыщенность s
.
Исключим градиент давления
/
px
∂∂
, поделив почленно одно на
другое уравнения (28.1):
0
()
()
ввв
ннн
wQks
wQks
η
== , (28.8)
где введено обозначение
0
/
вн
ηηη
=
.
Применив к (28.8) правило производных пропорций и использовав
(28.7), получим

0
()
()()()()
ввв
вн
wQks
wtQtksks
η
==
+
.
Обозначив
0
()
()
()()
в
вн
ks
fs
ksks
η
=
+
, (28.9)
из предыдущего равенства найдем:
()()
и [1()]()
вн
wfswtwfswt
==−
. (28.10)
Введенная здесь функция насыщенности f(s)
, называемая функцией распределения потоков фаз
или функцией Бакли-Леверетта, имеет простой физический смысл. Из (28.10) следует. что f(s)
,
представляющая отношение скорости фильтрации (или расхода) вытесняю
щей фазы (воды) и
суммарной скорости w (или расхода Q), равна объемной доле воды в суммарном по
токе двух фаз.
Функция f(s), как мы убедимся в дальней
шем, играет важную роль при гидродинамических расчетах
двухфазных потоков, определяет полноту вытеснения и характер распре
деления насыщенности по
пласту. Как видно из (28.9), функция f(s) полностью определяется относительными фа
зовыми
проницаемостями. С ростом водонасышенности f(s)
монотонно возрастает от 0 до 1. Характерная
особенность графика f(s) - наличие точки перегиба с насыщенностью
п
η
,
участков вогнутости и
выпуклости, где вторая производная
()
fs
′′
со
ответственно больше и меньше нуля. Эта особенность в
большой степени определяет специфику фильтрационных задач вытеснения в рамках модели Бакли-
Леверетта (по сравнению, например, с задачами распространения ударных волн в газовой динимике).
Подставив теперь равенство (28.10) для w
в
в уравнение (28.3). получим
()
()0
sfs
mwt
tx
∂∂
+=
∂∂
. (28.11)
Поскольку насыщенность есть функция двух переменных s=s(x,t), то,
применяя правило
дифференцирования сложной функции к слагаемому
[ ]
(,)
fsxt
t
∂
∂
, что дает

()()
()
fsdfsss
fs
xdxxx
∂∂∂
′
==
∂∂∂
,
приведем окончательно (28.11) к уравнению
()()0
ss
mwtfs
tx
∂∂
′
+=
∂∂
. (28.12)
которое является дифференциальным уравнением только относительно насыщенности
. Изменение
насыщенности во времени по пласту можно получить в результате решения уравнения (2
8.12)
независимо от распределения давления p(x,t). Это уравнение известно в литера
туре как уравнение
Бакли-Леверетта.
Для нахождения распределения насыщенности к уравнению (2
8.12) нужно добавить начальное и
граничное условия:
при t=0
(,0)(),0
sxxx
ϕ
=>
,
при
0(0,)(),0
xstxt
ψ
==>
. (28.13)
В некоторых случаях можно считать, что
0
()const
при 0
xst
ϕ
===
, (28.14)
0
()const
при 0
tsx
ψ
===
.
Это - случай кусочно-постоянных начальных данных, имеющий важ
ное значение для
практических приложений. Величина начальной водо-насыщенносги s
о
влияет на процесс заводнения и
определяет структуру зоны вытеснения.
В дальнейшем для простоты будем считать суммарную скорость фильтрации w(t)
(а значит, и
суммарный расход Q) постоянной величиной:
w(t)=w=const; Q(t)=Q=const.
Лекция 33
Решение уравнения Бакли- Леверетта.
В проц
ессе нагнетания воды в пласт ее насыщенность будет меняться со временем вдоль
направления движения x. Связь между s, x и t можно записать в функциональной форме s=s(x,t)
или, что
эквивалентно, в дифференциальной форме

.
ss
dsdxdt
xt
(28.15)
Рассмотрим на плоскости (x,t) такие линии x(t), вдоль которых
насыщенность принимает
заданное посто
янное значение. Эти линии называют изосатами. Тогда для любого заданного значения
можно установить такую связь между x и t, что удовлетворяется уравнение s=s(x,t)=const
или
эквивалентное дифференциальное уравнение
0.
ss
dxdt
xt
Таким образом, линия распространения заданной насыщенности, т. е. связь между x и t
при
фиксированном s, получается совместным решением уравнений (28.12) и (28.15) при ds
= 0. Другими
словами, следует совместно решить следующие два уравнения:
()0; 0.
ssss
mwfsdtdx
txtx
(2
8.16)
Решение системы уравнений (28.16) дает соотношение между x и t в дифференциальной форме.
Чтобы система однородных, линейных относительно
/
st
∂∂
и
/
sx
∂∂
уравнений (2
8.16) имела
отличное от нуля (или. как говорят, нетривиальное) ре
шение, нужно, чтобы ее определитель был равен
нулю, т. е.
()
0,
mwfs
dtdx
откуда находим:
().
dxw
fs
dtm
(28.17)
Напомним, что производная dx/dt вычисляется при постоянном значении s, т.е.
/(/)
s
dxdtxt
=∂∂
.
Уравнение (28.17) можно проинтерпретировать следующим образом:
точка с постоянной
насыщенностью s (на кривой s(x) движется с постоянной скоростью, пропорциональной w/m, и явля
ется
функцией самой насыщенности.
Поскольку правая часть (28.17) постоянна, то уравнение (2
8.17) можно проинтегрировать и найти
положение x заданного значения насыщенности как функцию времени:
0
()(),
w
xsfstx
m
(28.18)
где x
0
- значения координат с начальной водонасыщенностью s
0
при t=0. Поскольку
f
′
и x
0
, являются
функциями s, то при помощи (2
8.18) можно построить полный профиль насыщенности в любой момент
времени t, вычисляя x для различных значений х.
Будем предполагать, что первоначально пласт был
насыщен нефтью и содержал лишь связанную (неподвижную) воду, так что в условиях (2
8.14) имеем:
0
1
ss
•
≤≤
, а начальная водонасыщенность (s
0
) такова, что
0
0
ss
•
<≤
и сосредоточена в момент t
= 0 в
сечении x = 0. т. е. x
0
= 0 в формуле (28.18).
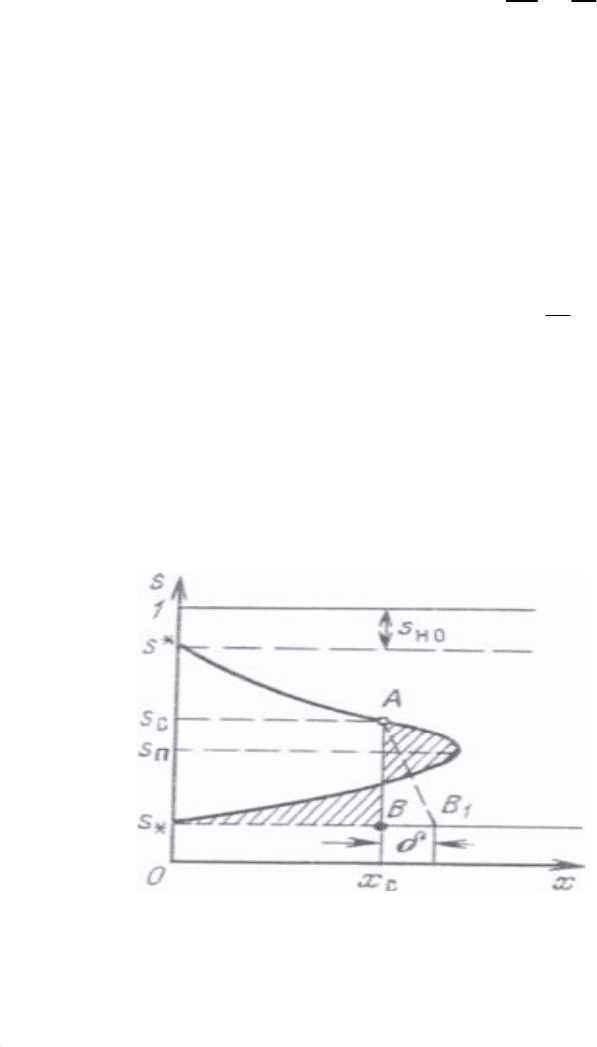
Рис. 28.1. Схематичный профиль насыщенности.

При t = 0 все точки кривой s(x), для которых s имеет значения, большие
s
•
и меньшие
1
но
ss
•
=−
,
где
но
s
остаточная нефтенасыщенность, начнут перемещаться в пласте, как следует из (2
8.17), со
скоростями, пропорциональными
()
fs
′
. Поэтому если известно
()
fs
′
для каждого значения s
, то
известна и скорость каждой точки движущейся кривой s(x). Kривая
()
fs
′
-
не монотонная функция, а
имеет максимум в некоторой точке. Это означает в соответствии с (2
8.17), что на движущейся кривой
s(x) некоторые промежуточные значения
насыщенности будут перемещаться быстрее, чем значения
насыщенности большие или меньшие. И спустя определенный про
межуток времени после начала
вытеснения форма профиля насыщенности будет иметь вид, подобный график
()
fs
′
на рис. 28.1
. Из
рисунка видно, что для любого значения x
насыщенность становится неоднозначной (имеет три
различных значения). Такое положение физически невозможно и, следовательно, начиная с этого
момента времени, невозможно непосредственное применение уравнения (28.18). Это застав
ляет нас
вспомнить, что урав
нения, описывающие совместное течение воды и нефти, были получены при
подразумеваемом предположении, что решение для профиля насыщенности - непре
рывная и гладкая
функция x и t. Поэтому дифференциальное уравнение (2
8.12) не применимо в области, где профиль
насыщенности или тангенс угла его наклона (т. е.
/)
xs
∂∂
терпит разрыв или имеет скачок.
Введение скачка (или фронта) насыщенности (прямая АВ на рис. 28.1) позволяет устран
ить
многозначность решения. Положение скачка насыщенности определяется из условия материального
баланса на скачке, так что площади сегментов, заштрихованные на рис. 28.1. равны.
Условие на скачке насыщенности. Рассмотрим условия сохранения массы каждой из
фаз при
прохождении разрыва через некоторый элемент объема порист
ой среды, ограниченный двумя
поверхностями
-
и
+
ΣΣ
по обе стороны от разрыва насыщенности (фронт).
Из законов сохранения массы воды и массы нефти получим соотношения
.
()
cBB
c
dxwwwff
v
dtmssmss
(28.19)
