Power electronic handbook

Подождите немного. Документ загружается.

41 Computer Simulation of Power Electronics and Motor Drives 1129

−

Load

Mechanical Model:

Electrical Model:

GAIN = 1

Hsq

Rs_q

LsI_q

I_sq

I_sd

I_rd

{1.5*@LM*@POLES/2}

I_sq

I_sd

I_rd

I_rq

E_Tsum

IN1+

IN1− OUT+

IN2+ OUT−

IN2−

Hsd

Rs_d

{@R_STAT}

LsI_d

{@R_STAT}

{@LSL}

ESUM

{@LSL}

{@LRL}

LrI_d

Rr_d

Rr_q

Lmag_d

Lmag_q

Lrl_q

l_sd

l_sq

l_rd

l_rq

{@OMEGA_INIT}

{1/@J_MOT}

Torque

OMEGA_mech

{@LM}

{@LRL}

{@R_ROT}

{@LM}

GAIN = 1

Hrd

Hrq

H_Load

Omech

Om_e

Torque

{@POLES/2}

Rotational Voltages:

(V(%IN1)

*@LM

+V(%IN2)

*@LR)

(–1)*(V(%IN1)

*@LM

+V(%IN2)

*@LR)

−

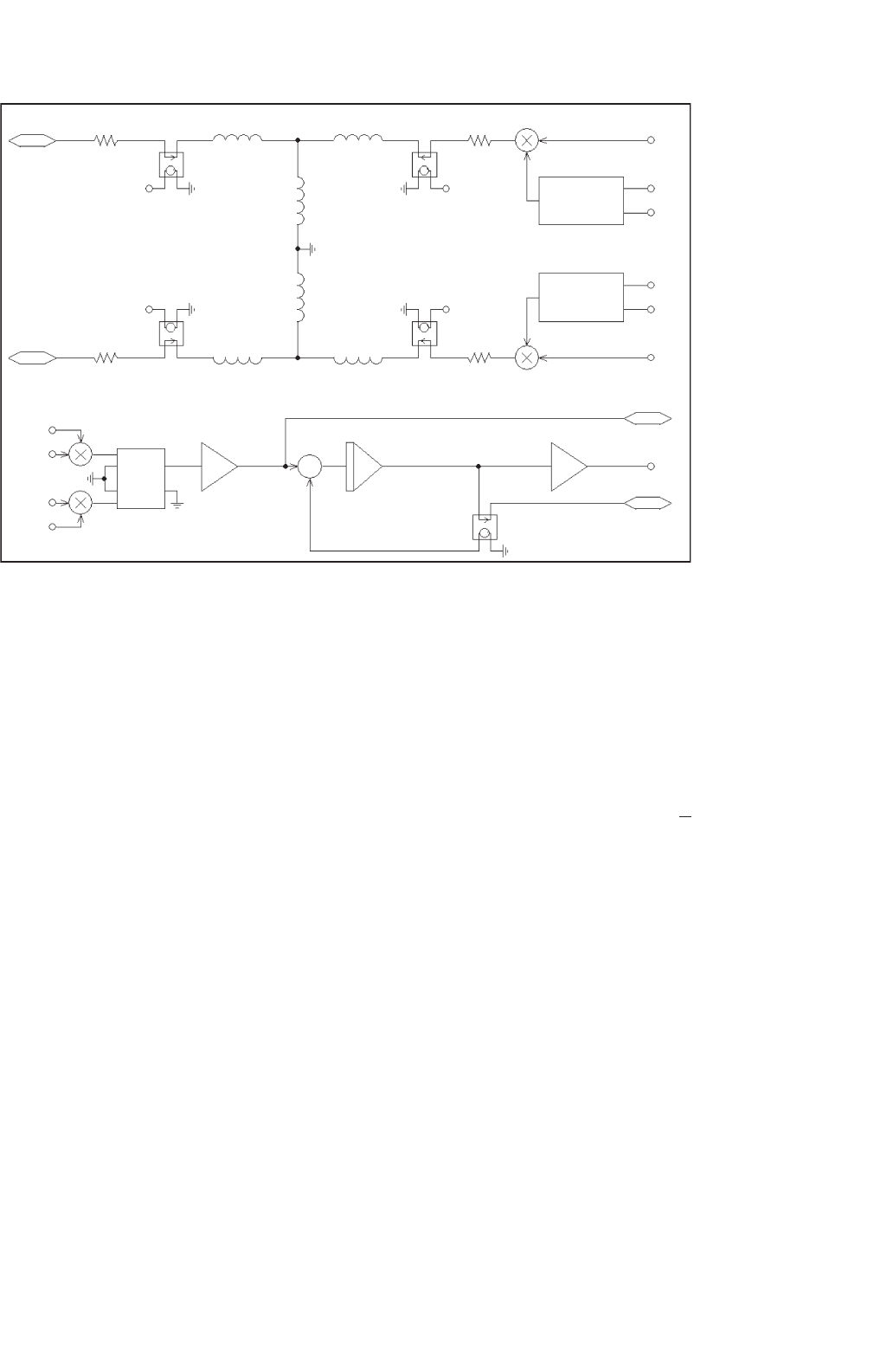
FIGURE 41.9 Subcircuit for induction motor model.

in this way is that several symbols can call one set of subcircuits

with different parameters.

Right-clicking on the motor symbol and selecting “Descend

Hierarchy” reveals the associated subcircuit that implements

its function. This subcircuit is shown in Fig. 41.9. The upper

portion of this subcircuit represents the electrical model. The

task of the electrical model is to calculate the stator and rotor

currents, with the stator voltages and the mechanical speed

of the machine being input parameters. However, it is also

possible without any changes, to feed stator currents (with

controlled current sources) into the D and Q inputs and have

the model to calculate the appropriate stator voltages. This

option is useful for vector control applications, which are

discussed later.

The equation system for the electrical model of a two-phase

induction machine is given by Eq. (41.3). The theory for this

equation system is derived in [2, 3, 6, 7]. The equation sys-

tem and the model are formulated for the stationary reference

frame. This reference frame assumes that the frame of the

machine is stationary (which is hopefully the case in a real

machine!) and the voltages and currents of the rotor are equiv-

alent AC values with stator frequency. From machine theory

we know that the actual rotor currents have slip frequency.

Another reference frame is the synchronous (also called exci-

tation) reference frame. In this reference frame, the stator of

a ﬁctitious machine is assumed to rotate with synchronous

speed. The advantage of this reference frame is that the input

frequency is zero (DC), which makes it easy to explain the

principle of vector control by extending the theory of DC

machines to AC machines.



















stat

+pL

0 pL

0 R

stat

+pL

0 pL

rot

+pL

−ω

rot

+pL



















p =

(41.3)

In typical implementations of vector control using digital

signal processors (DSPs), the synchronous reference frame is

used internally to calculate the reference values for the currents

in the D and Q axis. These values are then transformed to the

stationary reference frame in an additional step. Sometimes

still other reference frames are used and it is possible to gen-

erate a universal electrical model with a reference frame speed

input. This model could then be used for any reference frame.

The electrical model in Fig. 41.9 implements the equation

system shown in Eq. (41.3). The circuit closely resembles the

well-known T-equivalent circuit for the steady-state analysis of

induction machines. Two instances of the T-equivalent circuit

are necessary to implement the two-phase (D, Q) model. The

two instances of the circuit are almost mirror images of each

other (and actually drawn that way) except for some differ-

ences in the circuit elements that calculate the voltages, which

are generated due to the rotation of the rotor. The bottom of

1130 M. Giesselmann

Fig. 41.9 represents the mechanical model. This circuitry cal-

culates the internally generated electro-magnetic torque, using

the rotor and stator currents as input values. The equation for

the internal electromagnetic torque of the induction machine

is given by Eq. (41.4) [3, 6, 7]. The factor 3/2 accounts for the

fact that the real motor is a three-phase machine. Using the

generated torque, the load torque, and the moment of inertia,

the angular acceleration can be calculated. Integration of the

angular acceleration yields the rotor speed, which is used in

the electrical model. To avoid clutter and to improve readabil-

ity, connection bubbles are used to connect the various parts

of the model together.

T =



−I



(41.4)

Since typical induction machines are three-phase machines,

it is often desirable to have a machine model with a three-

phase input. Therefore, a bidirectional two-phase to three-

phase converter module, which can be attached to the motor,

has been developed. A subcircuit for this module is shown in

Fig. 41.10. This circuit is truly bidirectional, meaning that the

circuit can be fed with voltage or current sources from either

side. The equation system for this voltage and current invariant

transformation is given by Eq. (41.5). This transformation is

sometimes called “Clark” or “ABC–DQ” transformation. Note

that V

denotes a zero-sequence voltage, which is assumed to

be zero. This voltage would only have non-zero values for

unbalanced conditions. An interesting detail of the subcircuit

is the three-phase switch on the input. This switch is necessary

to ensure a stable initialization of the simulator in case the

machine is fed with a controlled current source. The switch

Simulation Startup Support

for Current Source Drive

GAIN = 1

RON = 500

ROFF = 50k

TOFF = 1ms

V(%IN)

−V(%IN1)/2

+sqrt(3)

∗

V(%IN2)/2

−V(%IN1)/2

−sqrt(3)

∗

V(%IN2)/2

(V(%IN1)

−V(%IN2)/2

−V(%IN3)/2

*2/3

(V(%IN1)

-(V(%IN2))

/SQRT(3)

ABC <−> DQ Transformation:

GAIN = 1

H_d

H_q

FIGURE 41.10 Subcircuit for the ABC–DQ transformation module.

provides an initial shunt resistor from the three-phase input to

ground. Soon after the simulation has started, the switch opens

and leaves only a negligible shunt conductance to ground.













2 −1 −1

√

3 −

√

11 1

























202

−1

√

−1 −

√













(41.5)

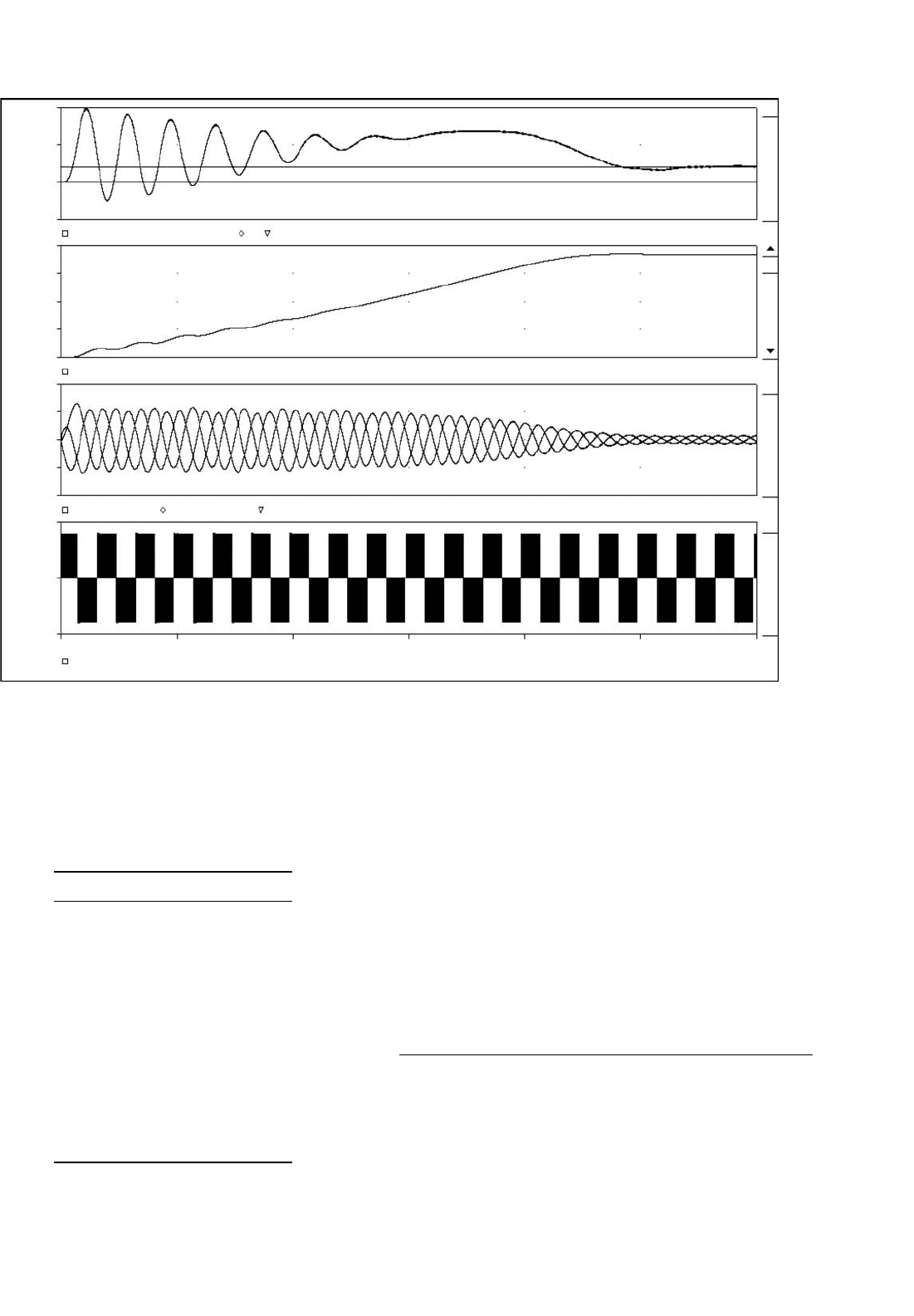
Figure 41.11 shows the result for the start-up of the induc-

tion motor for the circuit of Fig. 41.8. The motor is a half

(Attention LE(½)) hp, 208 V, 4-pole machine. The detailed

parameters are shown in Table 41.1. The PWM generation

was identical to the example shown in Fig. 41.4, except that

the switching frequency was 4 kHz and 21.1% of the third

harmonic has been added to each of the reference sinusoids

in order to increase the linear modulation range. The result-

ing reference waveform was then multiplied with 1.14, which

represented the maximum voltage for linear modulation. The

top trace in Fig. 41.11 shows the developed electromagnetic

torque, the level for the rated steady-state torque (4 Nm as

commanded by the load in Fig. 41.8) and the zero level. This

graph shows the typical oscillatory torque production of the

induction machine for an uncontrolled line start. The scale

for this graph is 1 V = 1 Nm. The graph below shows the

mechanical angular velocity with a scale of 1 V = 1 rad/s.

Below the graph for the rotor speed, all three input currents

are shown. It is evident, that the current traces are almost

perfect sinusoids, despite the fact that the input voltage is the

41 Computer Simulation of Power Electronics and Motor Drives 1131

−10

200V

150V

100V

50V

40A

20A

−20A

−40A

500V

−5000

SEL>>

Torque, 1V = 1Nm

V(Motor1:Torque_Monitor)

V(Motor1:Omech)

I(R_sense_a) I(R_sense_b) I(R_sense_c)

Rotor Speed, 1V = 1rad/s

Stator Currents

50ms

100ms 150ms

Time

200ms 250ms 300ms

V(A,B)

FIGURE 41.11 Induction motor start-up with three-phase inverter circuit.

TABLE 41.1 List of all attributes used

for the half (Attention LE:

(

1/2

)

)hp, 208 V,

four-pole induction motor in Fig. 41.8

Attributes:

PART = Induction_Servo

MODEL = Ind_Motor

TEMPLATE =

J_mot = 0.01

Omega_init = 0.0

Ls = (@Lm + @Lsl)

Lr = (@Lm + @Lrl)

Poles = 4

Tau_r = (@Lr/@R_Rot)

REFDES = Motor?

Lsl = 14.96mH

Lrl = 8.79mH

R_Stat = 3.60

R_Rot = 1.90

Lm = 424.41mH

PWM waveform shown in the bottom graph. Also, the trace

for the torque shows no discernable high frequency ripple.

The reason is, of course, that the motor windings are induc-

tive, and represent a low-pass ﬁlter for the applied voltages.

Nevertheless, recent research suggests that ﬁltering the out-

put voltage of the inverter is advantageous anyway, because

it signiﬁcantly reduces the voltage stress on the windings and

suppresses displacement currents through the bearings [8].

41.5 Simulations of AC Induction

Machines Using Field Oriented

(Vector) Control

The following examples will demonstrate the use of PSpice



for simulations of AC induction machines using ﬁeld oriented

control (FOC). Again, it is assumed that the reader is famil-

iar with the basics of induction machine theory. Often times,

FOC is also called vector control, and both expressions can

1132 M. Giesselmann

be used interchangeably. The FOC was proposed in the 1960s

by Hasse and Blaschke, working at the Technical University of

Darmstadt [9]. The basic idea of FOC is to inject currents into

the stator of an induction machine such that the magnetic

ﬂux level and the production of electromagnetic torque can

be independently controlled and the dynamics of the machine

resembles that of a separately excited DC machine (without

armature reaction; no cross coupling). The previously dis-

cussed two-phase model for the induction machine is very

helpful for studies of vector control and shall be used in

all examples. If a two-phase induction motor model for the

synchronous (or excitation) reference frame is used, the simi-

larities between the control of a separately excited DC machine

and vector control of an AC induction machine would be most

evident. In this case, the D input would correspond to the ﬁeld

excitation input of the DC machine and both inputs would

be fed with DC current. Assuming unsaturated machines, the

current into the D input of the induction machine or the

ﬁeld current in the DC machine would control the ﬂux level.

The Q input of the induction machine would correspond to

the armature winding input of the DC machine and again

both inputs would receive DC current. These currents would

directly control the production of electromagnetic torque with

a linear relation (constant k

) between the current level and

the torque level. Furthermore, the Q component of the current

would not change the ﬂux level established by the D compo-

nent (no cross coupling). To make such a simulation work,

it would ﬁnally be necessary to calculate the slip value that

corresponds to the commanded torque and supply this DC

value to the D, Q (synchronous reference frame) machine

model.

Of course this is very interesting from an academic stand-

point and the author uses this example in a semester long

lecture on FOC. However, it should again be noted, that a

machine represented by a model with a synchronous reference

frame would have a stator, which rotates with synchronous

speed. Of course this is not realistic and therefore it is more

interesting to generate a simulation example that uses the

previously discussed motor with a model for the stationary

reference frame. This motor must be supplied with AC volt-

ages and currents with a frequency determined mostly by the

rotor speed to a small extent by the commanded torque. We

still supply DC values representing the commanded ﬂux and

torque but we transform these DC values to appropriate AC

values. In the following example, we will assume that we can

measure the actual rotor speed with a sensor. This can, in

effect, be easily accomplished and many types of sensors are

available on the market. If we add the slip speed, that we

determine mathematically from the torque command, to the

measured rotor speed, we obtain the synchronous speed for

the given operating point. With this synchronous speed we can

transform the DC ﬂux and torque command values from the

synchronous reference frame to the stationary reference frame.

We accomplish this by using a rotational transformation

according to the matrix equations in Eq. (41.6). This rotational

transformation is also called “Park” transformation.



Dout

Qout





cos

(

)

−sin

(

)

sin

(

)

cos

(

)



Din

Qout





Dout

Qout





cos

(

)

sin

(

)

−sin

(

)

cos

(

)



Din

Qout



(41.6)



cos

(

)

−sin

(

)

sin

(

)

cos

(

)



cos

(

)

sin

(

)

−sin

(

)

cos

(

)







As shown in Eq. (41.6), the transformation is bidirectional

and the product of the transformation matrices yields the

unity matrix. For the following discussion we shall deﬁne the

transformation, which produces AC values from DC inputs

as a positive vector transformation and the reverse operation

consequently a negative vector transformation. The matrix

equation for the positive vector transformation is shown on

the left side of Eq. (41.6). The negative transformation is very

useful to extract DC values from AC voltages and currents

for diagnostic and feedback control purposes. We will also

make use of it for sensorless vector control, which is discussed

below. Both rotational transformations use the angle, ρ,inthe

equations. This angle can be interpreted as the momentary

rotational displacement angle between two Cartesian coordi-

nate systems; one containing the input values and the other,

the output values. This angle is obtained by integration of the

angular velocity with which the coordinate systems are rotating

(typically the synchronous speed).

In summary, we replaced a theoretical motor model using

a synchronous reference frame by a reference frame transfor-

mation of the supply voltages and currents. In fact, modern

DSPs like the TMS320C2000™ Digital Signal Controller series

from Texas Instruments are capable to perform both the

Clark and the Park transformation in both directions at very

high speeds [10]. These DSPs are well supported with proven

reference designs, including free software examples.

Figure 41.12 shows the top level of a simulation example that

implements vector control for an induction machine with a

stationary reference frame model. In fact, the motor model and

the associated subcircuits are identical to the ones used for the

circuit shown in Fig. 41.8. However, a more powerful motor is

used here, speciﬁcally a 3 hp, 4-pole 208 V motor with circuit

parameters shown in Table 41.2. As discussed above, the actual

speed of the rotor is used as an input signal for the control unit.

This scheme is known as indirect vector control and repre-

sents one of the most often used arrangements. The symbol

for the controller has the same parameters as the motor. This

is necessary to achieve correct ﬁeld orientation. In real sys-

tems, the controller also must know or somehow determine

the machine parameters. The machine parameters could have

also been established globally using “PARAM” symbols, but

if the parameters for the controller can be set separately as it

is the case here, the inﬂuence of parameter mismatch on the

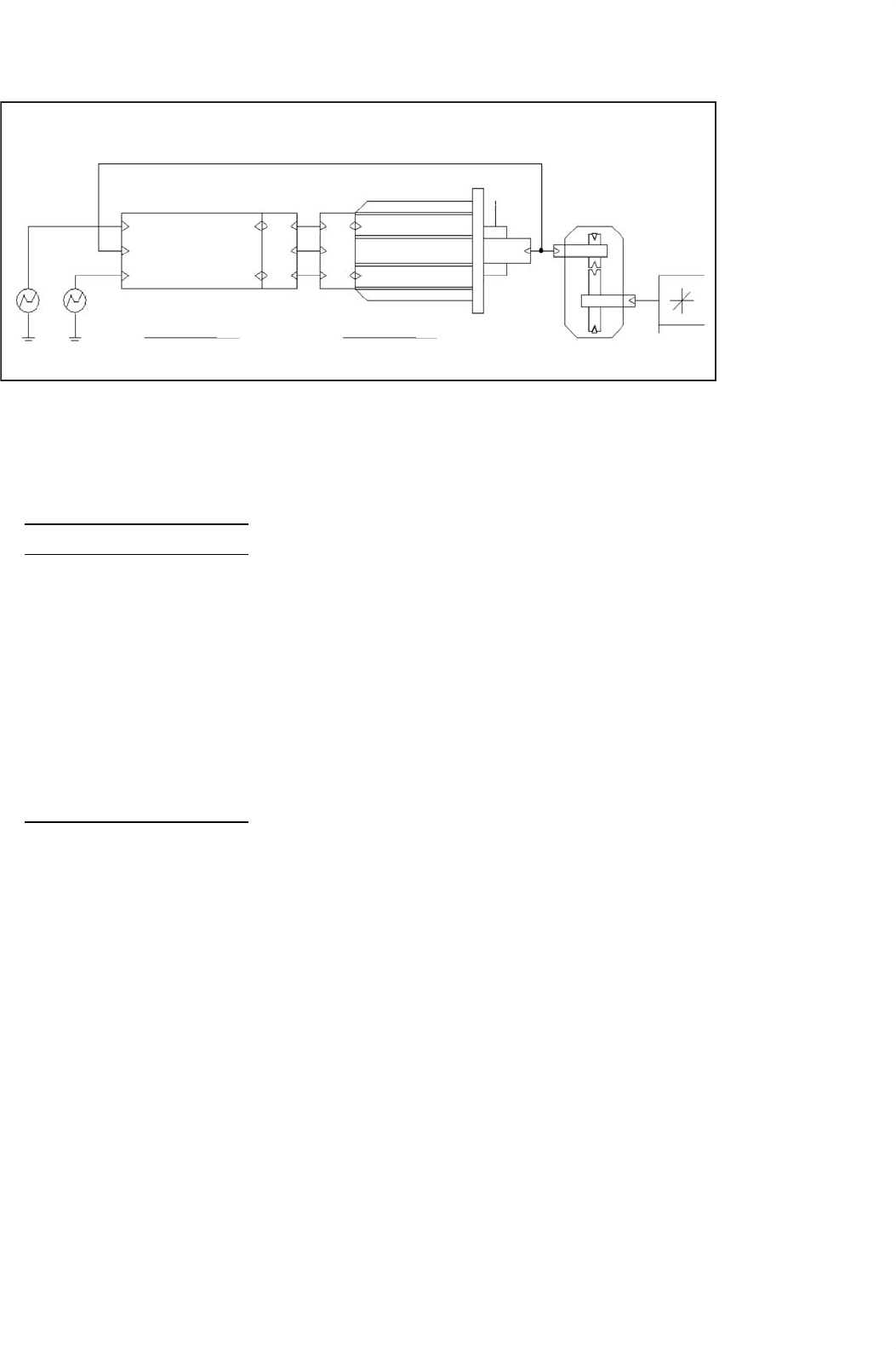
41 Computer Simulation of Power Electronics and Motor Drives 1133

24.5

PARAMETERS:PARAMETERS:

Indirect Vector Control of an Induction Motor:

Omega_mech

Vector Controller

Vector_Control1

Motor1

Torque

Omech

QQC C

Torque

V_TorqueV_Flux

Flux

Gear1

RATIO = 0.5

880 RPM

Nm @

Lin_Load1

Induction_Servo

V_LL = 208

V_PH_PK = {Sqrt(2)*V_LL/sqrt(3)}

PSI_N = {V_ph_pk/Omega_n}

FREQ_N = 60

OMEGA_N={2*PI*Freq_n}

PI = 3.14159265

−

FIGURE 41.12 Top level circuit for indirect vector control of induction motors.

TABLE 41.2 List of all attributes for

the induction motor symbol for vector

control

Attributes:

PART = Induction_Servo

MODEL = Ind_Motor

TEMPLATE =

J_mot = 0.1

Omega_init = 0.0

Ls = (@Lm + @Lsl)

Lr = (@Lm + @Lrl)

Poles = 4

Tau_r = (@Lr/@R_Rot)

REFDES = Motor?

Lsl = 2.18mH

Lrl = 2.89mH

R_Stat = 0.48

R_Rot = 0.358

Lm = 51.25mH

performance of the control can be easily studied. An example

of this is given in Fig. 41.12.

Figure 41.12 also shows a symbol for a mechanical gear,

which is attached to the output of the induction motor. Let

us recall that the voltage on the mechanical output terminal

represents the angular velocity and the current represents the

torque. We also know that the product of the angular velocity

and the torque is the mechanical power. Therefore it is easily

understood that the electrical representation of an ideal gear

is an ideal transformer. The ideal transformer changes speed

(voltage) and torque (current) just like an ideal gear. Also

there are no power losses in an ideal transformer as well as in

an ideal gear.

In this fashion, many more mechanical properties and

devices can be modeled. For example, a mechanical ﬂywheel is

simply represented by a capacitor to ground. Due to the scaling

factors for the angular velocity and the torque, a ﬂywheel with

J =1 kgm

would be a capacitor with C = 1 F. The compliance

of a drive-shaft (elastic twisting by the applied torque) can be

modeled by a series inductor. By including both capacitors and

inductors, effects like mechanical resonance can be included

in a model.

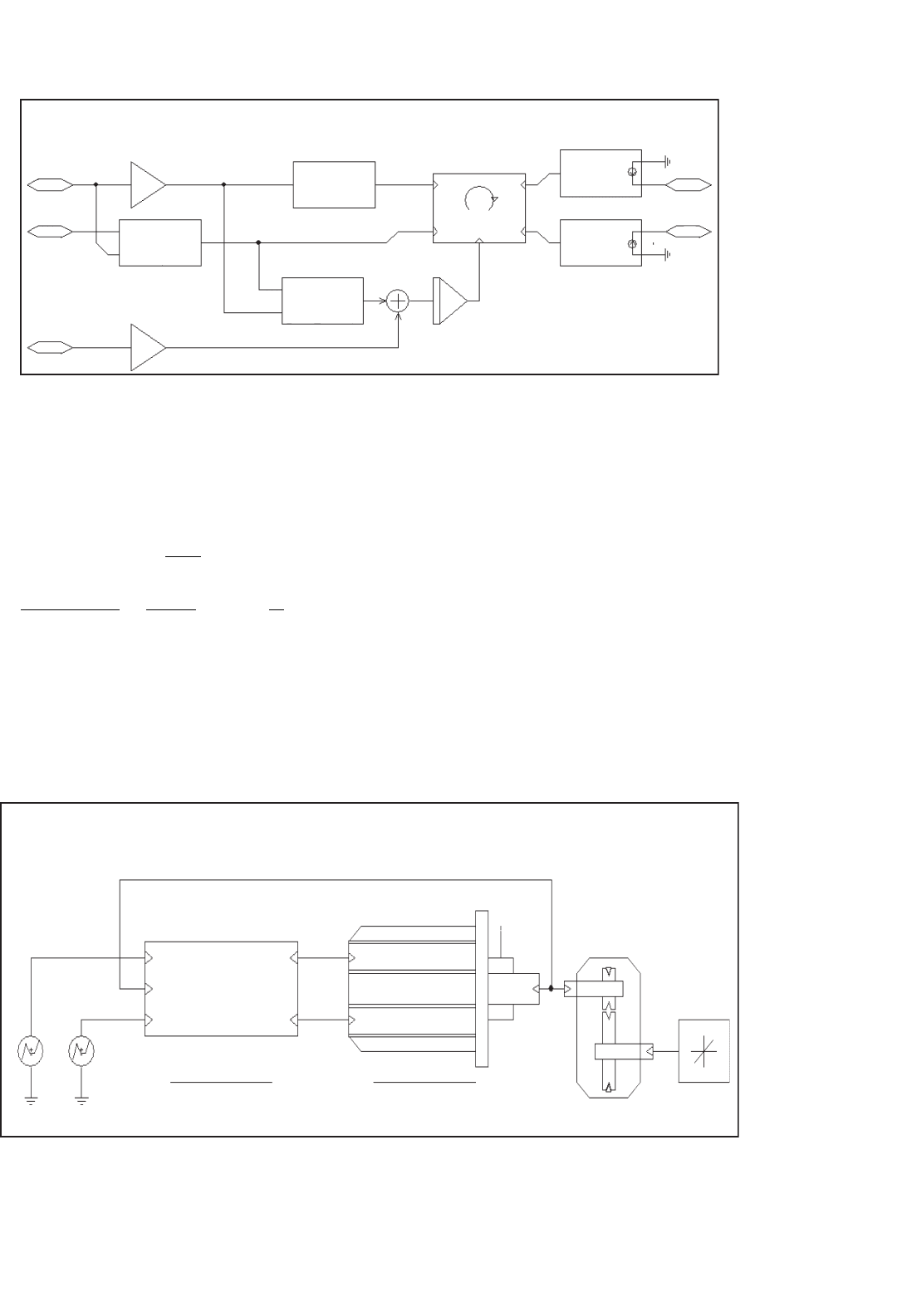
Figure 41.13 shows the subcircuit for the vector control

unit. The central part is a vector rotator for positive direction.

This element transforms the DC reference values for the ﬂux

(D-axis) and the torque (Q-axis) to the stationary reference

frame. The input angle for the vector rotator is the inte-

gral of the synchronous angular velocity. The signal called

“Omega_o” is the measured rotor speed.

This speed is multiplied with the number of pole-pairs

(poles/2) to obtain the electrical angular velocity. Then the

slip value (see Eq. (41.7) for slip frequency calculation for vec-

tor control) appropriate to the torque command is added and

the resulting signal is routed through an integrator to generate

the input angle for the vector rotator.

In the D-axis, a differentiator function “DDT()” is used in

a compensation (see Eq. (41.8) for D-axis reference current

for vector control) element which assures that the actual ﬂux

in the machine follows the commanded signal without delay.

The input and output values of the vector rotator are voltage

signals which correspond 1:1 to current signals. (In a real con-

troller the currents are typically scaled values in the memory of

a DSP.) In fact, the vector controller calculates the appropriate

currents that need to be injected into the machine to perform

as desired. Two voltage-controlled current sources with unity

gain are connected to the output of the vector rotator to gen-

erate these currents. In a real system, the controlled current

sources are realized by an inverter with current feedback. In

the most realistic case, this would be a three-phase inverter

and the ABC–DQ transformation would be performed before

the current controlled inverter. In this example, the ABC–DQ

transformation has been performed outside the controller and

1134 M. Giesselmann

Controller for Indirect Vector Control

Flux

Torque

Omech

{1/@LM}

I_sd_ref

I_sq

Vec Rot +

I_sd

In_D

In_Q

Out_Q

1.0

Omes_o

Out_D

V(%IN)

{@POLES/2}

V(%/N1)

(@KT*V(%IN2)

+10n)

V(%/IN1)

(V(%IN2)*

(@TAU_R+10n)

V(%/IN)+

DDT(V(%IN2))*

@TAU_R

Rho

FIGURE 41.13 Subcircuit for indirect vector control of induction motors.

the motor. This way, it is possible to study vector control

principles using a DQ controller and a DQ motor by elimi-

nating the ABC–DQ transformation elements. An example is

given in Fig. 41.14.

slip

= L

(41.7)



+τ



1 +τ

p =

(41.8)

Figure 41.15 shows the results obtained for the circuit shown

in Figs. 41.12 and 41.14 with perfect tuning of the vector

controller. Perfect tuning means that the controller precisely

knows all motor parameters at all times (including resistance

changes due to heating of the windings). The two traces in

Indirect Vector Control of an Induction Motor:

Vector_Control1

Flux

Vector Controller

Omech

Torque

V_TorqueV_Flux

PARAMETERS: PARAMETERS:

V_LL = 208

V_PH_PK = {Sqrt(2)*V_LL/sqrt(3)}

PSI_N = {V_ph_pk/Omega_n}

FREQ_N = 60

OMEGA_N = {2*Pi*Freq_n}

Pl = 3.14159265

Omega_mech

Motor1

Torque

Omech

Induction_Servo

Ratio = 0.5

24.5 Nm @

880 RPM

Lin_Load1

Gear1

FIGURE 41.14 Circuit for indirect vector control without ABC–DQ transformations.

the diagram on top of Fig. 41.15 represent the traces for the

D and Q input signals of the vector rotator. The graph below

shows the reference value for the ﬂux. It is evident, that the

ﬂux level is being changed at the same time when 10 Nm of

torque is commanded (and produced). This is done to check if

the torque and the ﬂux can be independently controlled, which

is true for correct FOC. Below the ﬂux reference is the graph

for the mechanical angular velocity. It can be seen, that the

machine accelerates whenever torque is developed and slows

down due to the load when the torque command is driven

to zero. The graph on the bottom of Fig. 41.15 provides the

easiest way to judge the quality of the correct ﬁeld orientation.

This graph shows the traces of the commanded and the actu-

ally produced torque and in this case they are perfectly on top

of each other at all times.

41 Computer Simulation of Power Electronics and Motor Drives 1135

20V

10V

750mV

500mV

250mV

50V

25V

15V

10V

0s 0.4s

V (Motor1: Torque)

V (Torque)

V (Omega_mech)

V (Flux)

V (Vector_Contr 1.I_sd) V (Vector_Contr I1.I_sq)

Current Command ID, 1V=1A

Current Command IQ, IV=1A

Flux Reference, 1V=1Vs

Mechanical Angular Velocity, 1V=1rad/s

Torque & Torque Command

0.8s

Time

1.2s 1.6s 2.0s

SEL〉〉

FIGURE 41.15 Results for indirect vector control with perfect tuning.

Figure 41.16 is an example of the results obtained from a

de-tuned vector controller. The circuit is identical to the cir-

cuit in Fig. 41.12, except for the fact that the rotor resistance

value in the controller was increased to 125%, which is thought

to be attributed to heating of the rotor bars. It is obvious

that the traces for the commanded and the actually produced

torque are no longer identical. This is especially true, during

times when the ﬂux is changing. De-tuning is actually a real

problem in industrial vector control applications. De-tuning

is caused by the fact that the machine parameters are not pre-

cisely known to begin with and/or, are changing during the

operation of the machine. The values of the winding resistance

are most likely to change due to heating of the machine.

41.6 Simulation of Sensorless Vector

Control Using PSpice

In the previous example, the advantages of vector control have

been shown. However, for the implementation of the control

scheme a sensor for the mechanical speed was necessary. This

could pose a problem for applications, where a vector control

unit is to be retroﬁtted into existing equipment. The motor

installation may not easily allow the installation of a mechan-

ical speed sensor. Therefore engineers have thought to replace

the mechanical speed sensor with a speed observer, which is

a mathematical model that is evaluated by the control pro-

cessor (typically a DSP), which is performing the standard

vector control computations anyway. The algorithm for the

observer would use the measured stator voltages and currents

for the D- and Q-axes as input parameters. It would also rely

on the knowledge of the machine model and on the correct

machine parameters (rotor and stator resistance, mutual and

leakage inductance, etc.). The following example shows such

an arrangement. It could be derived from the previous exam-

ple with the only difference being that the speed sensor signal

is replaced by a speed observer. However, careful examina-

tion of the derivation [2] of the speed observer reveals, that it

is easier to calculate the synchronous angular velocity, which

is ultimately desired anyway, than the angular velocity of the

rotor. Therefore, the observer was modiﬁed and the calcula-

tion of the rotor speed and the subsequent addition of the slip

speed was foregone. The speed observer used here basically

solves the D, Q equation system of the induction machine

shown in Eq. (41.3), with the only difference that some of

the dependent variables are now independent and vice versa.

In addition to the synchronous angular velocity, the observer

1136 M. Giesselmann

20V

10V

SEL〉〉

750mV

500mV

250mV

50V

25V

15V

10V

0s 0.4s

V (Motor1:Torque) V (Torque)

Torque & Torque Command

Mechanical Angular Velocity, 1V=1rad/s

Flux Reference, 1V=1Vs

Current Command ID, 1V=1A

V (Vector_ContrI1.I_sd)

V (Vector_ContrI1.I_sq)

Current Command IQ, 1V=1A

V (Flux)

V (Omega_mech)

0.8s 1.2s 1.6s 2.0s

Time

FIGURE 41.16 Results for indirect vector control with 125% rotor resistance.

provides the values of the rotor ﬂux, which are used in the

D-axis signal path. The advantage of this is that the compen-

sator with the differentiation function, which is problematic

from a numerical stability standpoint, can be eliminated.

Figure 41.17 shows the top level of a simulation project

for sensorless vector control. The top view of this circuit

is very similar to the circuit for the indirect vector control

represented by Figs. 41.12 and 41.14 except for the miss-

ing motor-speed feedback. The model for the motor and the

motor’s parameters are precisely the same as in the example

for the indirect vector control. Selecting the “Sensorless Vector

Control” block and choosing “Descend Hierarchy” reveals the

associated subcircuit, which is shown in Fig. 41.18. This sub-

circuit is similar to the subcircuit for the indirect vector control

with two exceptions: ﬁrst and foremost, the motor-speed feed-

back signal is replaced by the speed observer. In this case

the speed observer directly provides the synchronous angular

velocity. Therefore, it is not necessary to calculate the slip speed

and add it to the rotor speed to obtain the synchronous speed.

Second, the values of the rotor ﬂux, which are available from

the speed observer, are used to calculate the reference value

for the torque producing current (Q) component. Therefore,

the compensation term, which contains a differentiator in the

D-axis of the controller shown in Fig. 41.13 can be eliminated.

The purpose of the compensation term is to ensure that the

ﬂux is equal to the ﬂux command at all times with no delay.

If that is assured, the command signal can be chosen in place of

the real ﬂux to calculate how much torque producing current

is necessary to obtain the desired torque.

In order to demonstrate how to obtain a more compact

motor model, the extensive subcircuit of the induction motor

model (see Fig. 41.9) has been replaced by a number of addi-

tional attributes which have been added to the motor symbol

using the symbol editor.

However, if the actual ﬂux is known (observed), this value

can be used instead. Since the ﬂux observer is fed by the

D- and Q-axes voltages and currents for the stationary ref-

erence frame, the ﬂux components need to be transformed

back into the synchronous reference frame. This is done with

the “Negative Vector Rotator” located above and to the left of

the speed observer in Fig. 41.18.

The easiest way to start the symbol editor and to open the

appropriate library is to select the symbol by clicking into it

and then select the “Edit Symbol” function. The additional

attributes of the modiﬁed motor symbol will enter the equiv-

alent to the subcircuit represented by Fig. 41.9 into the netlist.

The netlist is a compilation of the schematic pages into a

textual description in ASCII format. From a usability stand-

point, a “self-contained” symbol like this is a very elegant

solution, since the ﬁle for the subcircuit is no longer required.

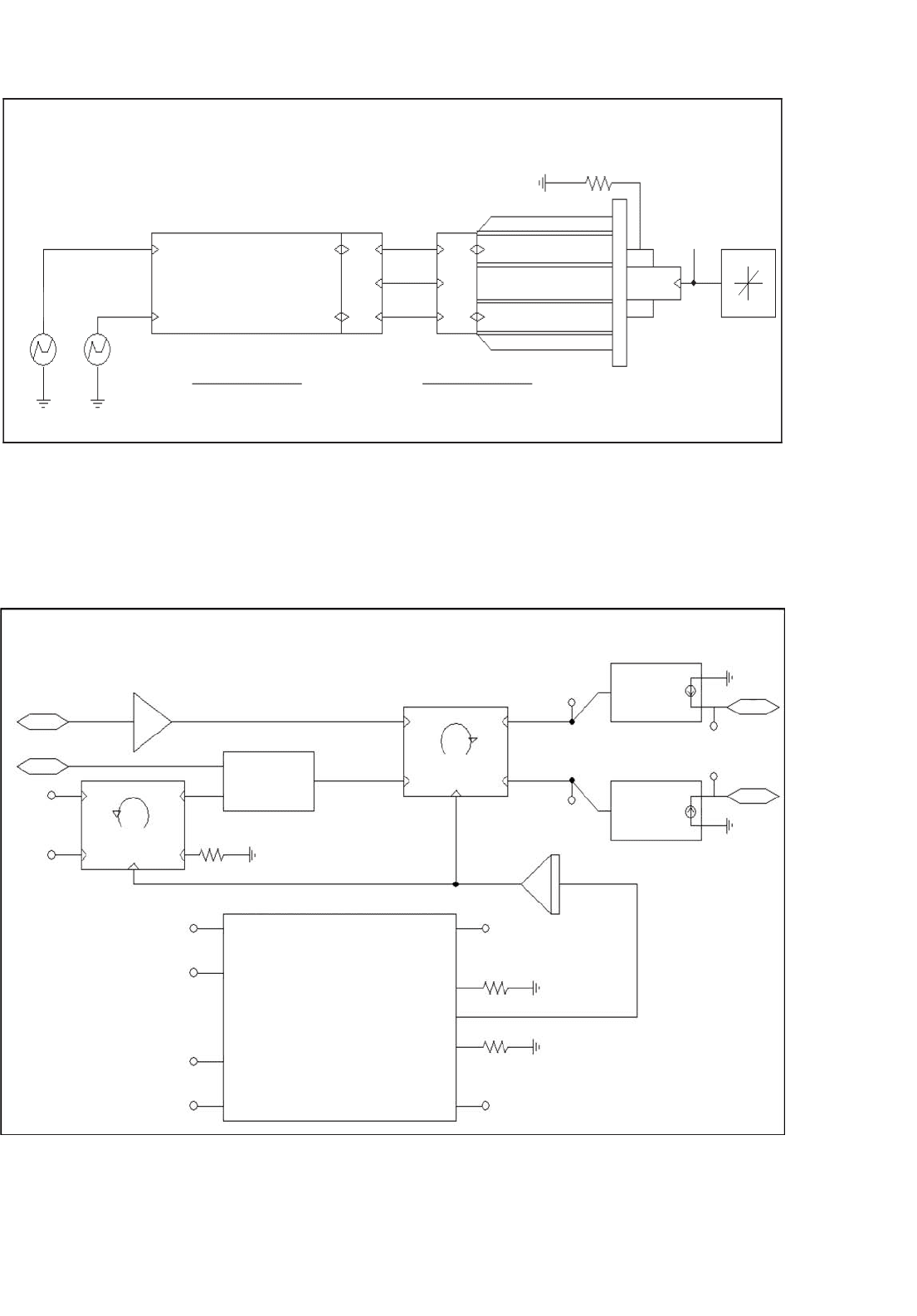
41 Computer Simulation of Power Electronics and Motor Drives 1137

Sensorless Vector Control of an Induction Motor

Flux

Reference

Flux

Motor 1

Rt 1k

Torque

Omech

Lin_Load1

12.25 Nm @

1760 RPM

V_Flux

NoSen_Vec_Control1

Sensorless Vector Control

Torque

PARAMETERS: PARAMETERS:

FREQ_N = 60

OMEGA_N = {2*Pi*Freq_n}

PI = 3.14159265

V_LL = 220

V_PH_PEAK = {sqrt(2)*V_LL/sqrt(3)}

PSI_N = {V_ph_peak/Omega_n}

Torque

−−

V_Torque

FIGURE 41.17 Top level of simulation circuit for sensorless vector control.

Flux

Torque

PsiD

PsiQ

{1/@LM}

I_sd

I_sq

Isd

I_d

Isq

V(%IN)

Controller for Sensorless Vector Control:

Speed Observer

V(%IN1)

(@KT*V(%IN2)

+10n)

Rt1

Speed_Observer1

V_d

I_sd

I_sq

V_q

I_d

I_q

V_q

V_d

In_D

Out_D

Out_Q

Rho

In_Q

Vec Rot -

In_D

Out_D

Out_Q

Rho

In_Q

Vec Rot +

Psi_d

PsiD

I_q

V_d

V_q

Psi_xr

OmSync

Psi_mag

Psi_q

PsiQ

Rt3

Rt2

1.0

FIGURE 41.18 Subcircuit for sensorless vector controller.

1138 M. Giesselmann

Since the PSpice



simulation engine always uses the netlist

as the input, the circuit works identically. For the PSpice



sim-

ulation it makes no difference, where the netlist or part of it

comes from. This also means that even the most recent release

of PSpice



can still simulate legacy ﬁles that have been created

before the introduction of schematic editors. The introduc-

tion of netlist entries is done via the “TEMPLATE” attribute.

This attribute is a system attribute and a part of every symbol.

Therefore, the TEMPLATE attribute is of course present in the

attribute list for the motor symbols in the previous examples.

These attribute lists are shown in Tables 41.1 and 41.2. In these

tables the TEMPLATE attribute has no value since the netlist

The format of the netlist entries for some common elements is:

[] denotes space holder for name extension speciﬁc for a symbol to avoid duplicate names.

Resistors, (R devices):

Generic: Rname[] +Node[] −Node[] Value ;Optional Comment

Example: Rsd[] Rsd+[] Rsd−[] 1.0k ;Resistor, ﬁxed Value

Example: Rsd[] Rsd+[] Rsd−[] {@Rs} ;Resistor, Value Rs passed on

Example: Rsd[] %D 0 1.0k ;Resistor, 1k, Pin ‘D’ to Gnd

Inductors, (L devices):

Generic: Lname[] +Node[] −Node[] Value ;Optional Comment

Example: Lsd[] Lsd+[] Lsd−[] 1.0u ;Inductor, 1.0 mH ﬁxed

Example: Lsd[] Lsd+[] Lsd−[] {@Lsl} ;Inductor, Value Lsl passed on

Voltage-controlled voltage sources (E devices):

Generic: Ename[] +Out[] −Out[] VALUE { Control Function }

Example: ETorque[] %Torque 0 VALUE { 1.5

∗

(Vt1[] – Vt2[]) }

;E source, output between pin “Torque” and Gnd, Control function as shown

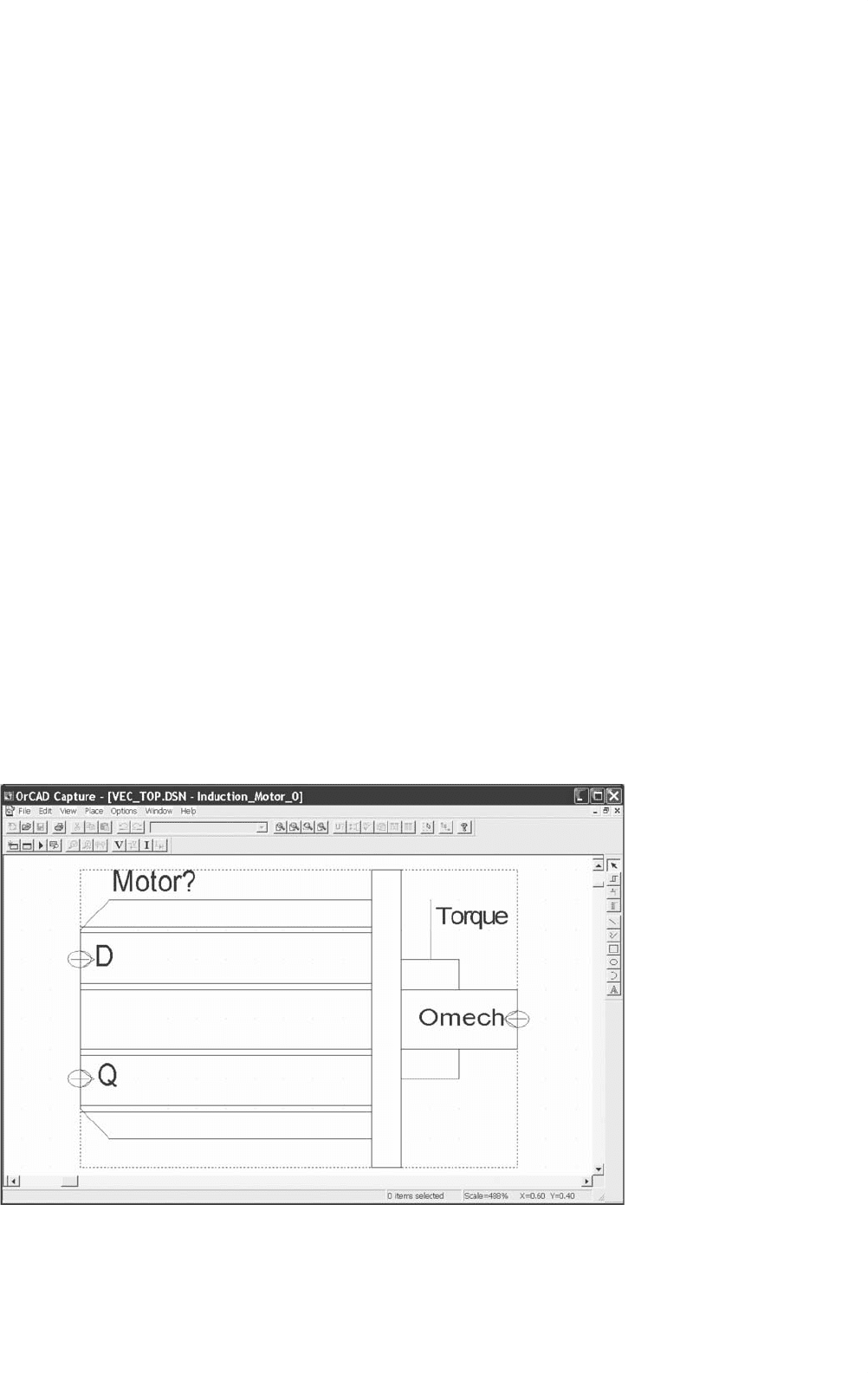
FIGURE 41.19 Screen view of motor symbol in the symbol editor.

entries are made by the symbols in the associated subcircuit.

To give a reader a better understanding of the self-contained

machine symbol, the format of some common netlist entries

and the syntax of the value of the TEMPLATE attribute is

discussed. It is also very helpful to examine the TEMPLATE

attributes of existing symbols.

Figure 41.19 shows the screen view of the symbol for the

induction motor in the symbol editor in PSpice



/Cadence

Release 9.1, which was used for the development of this part.

Figure 41.20 shows a similar view; however, here the window

for entry and editing of attributes is also visible. This screen

can be invoked using the “Options/Part Properties...” dialog.