Potter T.D., Colman B.R. (co-chief editors). The handbook of weather, climate, and water: dynamics, climate physical meteorology, weather systems, and measurements

Подождите немного. Документ загружается.

(NIST) or a manufacturer’s calibration sheet that came with the sensor. More

commonly, however, the sensor calibration is a variable with calibration temperature

points. It should be considered a conditional bias with the bias correction dependent

upon the temperature measured.

The precision term might be quite small, perhaps 0.02



C based on the standard

deviation of a series of measurements with the sensor at equilibrium in a constant

temperature thermal mass. This is really the precision of the measurement of resis-

tance with the resistance kept constant by the thermal mass. The size of this preci-

sion measurement may be an indicator of the quality of the thermal mass.

A much larger precision will be found if the test uses a collocated transfer

standard in the atmosphere. Functional precision (ASTM, 1990) is the root mean

square of the distrib ution of differences in measurements made with two identical

systems. The precision will be larger because the two sensors are not in the same

thermal mass. It will probably be on the order of a few tenths of a degree Celsius.

The uncertainty will contain the inﬂuence quantity. This is like saying that the

accuracy estimate is not complete until all of the siting and exposure errors are

considered. These are the large errors when deciding how good the measurements

are with respect to a speciﬁc application.

The inﬂuence quantities for the example of air temperature at 1.5 m above the

ground include the following:

 The heat gained by the sensor from solar radiation arriving directly or

indirectly by conduction, convection or reﬂection.

 The heat lost by the sensor to the night sky by radiation or conduction.

 Wind speed and, to a lesser extent, wind direction, as a modifying condition to

the heat loss of the shield. Possible effect on the forced aspiration rate.

 Cloud cover and time of day as a modifying condition to radiative heat transfer.

Also as a contributor to reﬂected radiation.

 Water droplets in the air or on the shield as a modiﬁer to the air sample being

measured. The relative humidit y is a secondary effect to evaporation rate.

 Surface condition, including snow cover, as a radiation reﬂector. Parallax error

for manually read liquid-in-glass thermometers.

The list can go on and on. The inﬂuence quantities will be different for different

measurands or variables.

Measurement instrument output values can be reported to any resolution with

modern digital systems. A sample measurement value should not be reported with a

resolution ﬁner than the uncertainty of the system. A sample air temperature value

should be reported to whole degrees. An average of many samples should be

reported to a tenth of a degree. Digital systems should carry sufﬁcient resolution

to avoid rounding er rors. Maximum or min imum values should be reported to a

tenth of a degree in order to preserve relative infor mation. The uncertainty of a

measurement will be much smaller in the context of a relative inquiry as opposed to

706 CHALLENGES OF MEASUREMENTS

an absolute value. Local measurement networks will have a relative uncertainty of

value to the network application.

A recent study (Lockhart, 1996) showed that modern automatic data systems still

fail to consider the need to maintain resolution for output values. In Lockhart (1979)

it was shown that fastest-mile measurements were taken in integer knots and

reported for climatological applications in miles per hour. The unit conversion

was made with an integer table where the value of 19 mph could not exist, along

with many other values. The modern ASOS (Automated Surface Observing System)

takes measurements in knots but supplies daily summary data in miles per hour. The

unit conversion method does not have the resolution to allow every integer to appear.

There is still no 19 mph.

4 VALUE OF COMMON SENSE

During the process of writing a revision to the EPA Quality Assurance Hand book for

Air Pollution Measurement Systems, Volume IV, Meteorological Measurements

(EPA600=4-90-003), several subjects arose that could be resolved only by appeal

to common sense. In the more than 30 workshops that have followed the publication

of Volume IV, one appeal that is always made is to use common sense. When all else

fails, common sense is a good standard.

For example, one always ﬁnds the requirement that calibrations be ‘‘traceable’’ to

National Bureau of Standards (NBS) [now National Institute of Standards and

Technology (NIST)]. What does this mean and how does one document the compli-

ance with the requirement? The common interpretation is that there needs to be some

anemometer calibration at NIST that starts the transfer standard path. It might go to

another wind tunnel where the NIST calibration is transferred to the new wind

tunnel. A calibration in the new wind tunnel might be further transferred to a

third wind tunnel. A series of documents could be in the ﬁle that records all these

calibrations. The operator of the third wind tunnel might provide calibrations trace-

able to NIST.

A paper trail is not enough when there is a possibility of error in the process. Two

cases come to mind. The calibration at NIST has some uncertainty (NIST). Occa-

sionally there is an outlier. The prudent summarization of a NIST calibration is a

linear regression analysis, looking critically at differences at each point. Most

mechanical anemometers are linear once the nonlinear starting speeds are passed.

Outliers or problems with the calibration can usually be seen with this analysis. One

wind tunnel operator transferred each point of the NIST calibration to a new anem-

ometer, even the one obvious outlier in the NIST data. This was defendable on paper

but failed the common sense test.

Technology is always improving. Cup anemometers block some of the ﬂow in a

wind tunnel. How much is not well known. The amount varies with the design of the

anemometer but also with the size of the wind tunnel test section. Common sense

says that a cup anemometer calibrated in the large test section at NIST (3.25 m

) will

have a small blockage error, probably 1% or less. When the calibrated anemometer

4 VALUE OF COMMON SENSE 707

is used in a smaller wind tunnel with a test section of 0.4 m

, there will be more

blockage. If the calibration method involves transferring the NIST wind speeds to the

wind tunnel fan rpm and then transferring the wind tunnel fan rpm to another

identical anemometer, the blockage cancels out. Common sense says you can

ignore the blockage effect. If, on the other hand, the wind tunnel fan rpm is used

to ‘‘calibrate’’ a different kind of anemometer, the relative blockage of each anemo-

meter in the small test section must be known. Since this effect is difﬁcult to

quantify, it is comm on sense to use NIST transfer standards for each type o f anem-

ometer of interest.

When, in the past, wet-bulb and dry-bulb temperatures were measured with a

sling psychrometer, it was a new technology. Other met hods for measuring dew-

point temperature and relative humidity allowed for difference comparisons to be

made. Then it became clear that siting bias was a big problem for the sling

psychrometers. Even if the thermometer is moving rapidly, any incident solar radia-

tion will heat the thermometer. If shade is found, there may still be a problem with

reﬂected radiation. Body heat and humidity can bias the reading by modifying the air

if the thermometer is down wind of the operator. Understanding the meas urement

process and the application of common sense will minimize these errors.

A very accurate air pressure transducer can be calibrated in the laboratory but

when it is installed in the atmosphere the wind effect must be considered. Static ports

are now available to minimize wind pressure effects, but two or more decades ago

the exposure of the pressure transducer was not considered. The transducer would be

mounted in a weatherproof box, but the inside box pressure was assumed to be the

same as atmospheric pressure. When the wind was blowing, there was a bias,

conditional on the speed and direction of the wind, which could be several times

the calibration uncertainty. The common sense in this example must be uncommon

until the knowledge of such effects reaches the operational meteorologist who must

make decisions about the design of the instrument systems.

There is an ‘‘ofﬁcial’’ data archive for the United States at the National Climatic

Data Center (NCDC) in Asheville, North Carolina. If one needs a copy of the

‘‘ofﬁcial’’ data for some purpose, often related to some lawsuit, one can get it

from NCDC. It comes designated as ofﬁcial and, no doubt, judges and juries are

duly impressed. It is true that the copy is certiﬁed to be correct by the head of

NCDC, but this does not say anything about the accuracy of the data. The National

Weather Service is responsible for the accuracy of the measurem ents it makes, while

NCDC is responsible only for faithfully recording the NWS numbers and copying

them when required (although NCDC does perform certain quality control checks

for continuity, etc.)

EPA and National Research Council (NRC) list the performance speciﬁcations

required for measurement systems used on projects under their author ity. Perfor-

mance audits are usually required on a periodic schedule to verify that the systems

meet those speciﬁcations. The auditor may use auditing methods designed to docu-

ment conformance. For wind speed there are two tests. One is starting threshold,

measuring the starting torque of the shaft and bearings with the cup wheel or

propeller removed. Bearings will degrade over time. The time is a function of the

708 CHALLENGES OF MEASUREMENTS

exposure environment. There is a starting torque that has been shown to be equiva-

lent of 0.5 m=s. The audit will document the starting torque expressed as a speed. If

the result is 0.6 m=s and the requirement is 0.5 m=s, are all of the speed data

rejected? If the last audit was 6 months ago, perhaps only the last 30 days of data

will be rejected since the bearings will degrade with time. The application of

common sense by the auditor, operator, and regulator will result in keeping all the

data. The bearings would be changed, but the perfor mance of the anemometer was

probably acceptable. The wind in the atmosphere does not start at steady slow speeds

as the wind tunnel test requires. The simulation of starting speed by starting torque

has some uncertainty.

If the audit showed a starting speed of 2 m=s, the answer becomes more difﬁcult.

The operator should examine the speed data for the 6 months or year since the last

audit where the starting speed was shown to be 0.4 m=s. Perhaps the record will

show a period where something happened to the anemometer. If the site is windy,

there may not be many periods with winds less than 2 m=s, in which case a higher

starting speed would not degrade the data. Common sense and critical examination

will suggest an answer to which the regulator and operator will agree. The last

answer to accept is the auditor rejecting all the speed data because of the starting

torque test results.

The other auditing method for anemometers is imposing a series of known rates

of rotation to the anemometer shaft. This challenges the ability of the measurement

system to sense the rate of rotation of the shaft and express this rate in terms of wind

speed at the output of the system. When the sensor output is a frequency and the data

logger is digital, the test will always pass. The only thing being challenged is the

ability of the system to count pulses and apply an algorithm to express frequency as

speed. There is nothing in this test that conﬁrms the algorithm of wind speed to

frequency. This takes a wind tunnel test or the acceptance of the manufacturer’s

claim that the generic transfer function for the product is correct.

When dealing with regulators, operators, and consultants, a common sense

discussion will usually result in an acceptable solution. What is even more important

is that it will result in the exchange of information that leaves all parties more

experienced and better prepared for the next question.

REFERENCES

ASTM (1990). Standard Practice for Determining the Operational Comparability of Meteor-

ological Measurements, ASTM, West Conshohocken, PA.

ISO (1993). Guide to the Expression of Uncertainty in Measurement (International Organiza-

tion for Standardization, Geneva, Switzerland), ISO=TAG 4 N 70 Rev. January.

Lockhart, T. J. (1979). Climate without 19 mph, Bull. Am. Meteor. Soc., 60, 660–661.

Lockhart, T. J. (1996). Wind climate data continuity study—II.

National Institute of Standards and Technology (1994). Guidelines for Evaluating and

Expressing the Uncertainity of NIST Measurement Results, NIST Technical Note 1297,

REFERENCES 709

Barry N. Taylor and Chris E. Kuyattt (Ed.), 12th International Conference on IIPS for

Meteorology, Oceanography, and Hydrology, Atlanta, GA , Jan. 28–Feb. 2.

Schneider, S. (1987). Discover October, p. 47.

Wieringa, J. (1992). J. Wind Engr. Ind. Aerodyn. 41, 357–368.

710

CHALLENGES OF MEASUREMENTS

CHAPTER 35

MEASUREMENT IN THE

ATMOSPHERE

JOHN HALLETT

The atmosphere is a turbulent medium. Any measurement is to be interpreted in the

context of a set of measurements in a time and spatial dimension having a variance

related to the scale considered. Such limits may be considered with respect to a fully

developed turbulent ﬁeld and limited by physical constraints—a solid boundary as at

the surface, a variable boundary as with motions limited by the stability co nstraint as

at an inversion top, or temporal as the diurnal or annual cycle. Any measurement is

made with an instrument with a given time and spatial characteristic—whether it be

a thermometer in sampling air ﬂow or a satellite remotely measuring emissivity from

a surface. The instrument design determines the lower limit of temporal and spatial

measurement scales through the response time and the size of the instrument.

Subsequent analysis determines how individual measurements are to be

combined—as a mean and variance time series at a given location or a spatial

ﬁeld at a given time as a conventional synoptic map, with the lower scale necessarily

limited through the initial instrument design. Such combinations of observations

have been a central theme of understanding the different processes in the atmosphere

and key in the initial development of meteorology (Fitz Roy, 1863; Brunt, 1917) and

have been long realized (Middleton and Spilhaus, 1953); (Handbook, 1956).

We make measurements in the atmosphere for a variety of reasons. On a local

scale, a measurement provides information for speciﬁc decisions, whether it be to

wear a sweater, to begin harvesting a crop or to cancel an aircraft take off. On a

broader scale, measurements are put together to provide information for a forecast

for similar decisions at remote places. Such synthesis is required for initialization of

a model of atmospheric processes whether it be to extrapolate frontal motion or to

Handbook of Weather, Climate, and Water: Dynamics, Climate, Physical Meteorology, Weather Systems,

and Measurements, Edited by Thomas D. Potter and Bradley R. Colman.

ISBN 0-471-21490-6 # 2003 John Wiley & Sons, Inc.

711

solve numerical ly the equations of motion leading to such progression. Further

synthesis may occur as such measurements are combined to give data to be used

for climatology as a design for living, in terms of means and departures therefrom to

estimate criteria for building design and for levels of investment in public utilities.

Crudely, the local measurement requires a scale of meters and a time of minutes ; the

synoptic scale the dimensi ons of Earth and times of days; the climatological use

requires a similar spatial scale but a time scale of a year to a decade or longer. Thus

our instruments must be sufﬁciently small to be used locally, yet sufﬁciently robust

and capable of calibration such that observations can be combined over extended

scales of time and space.

Instrument response may be of ﬁrst or second order depending on the nature of

the design. Thus, a standard thermometer responds to an environmental change by

approaching the new value almost exponentially and cannot overshoot. A wind vane,

on the other hand, that approaches a new direction can be (and usually is) designed

to overshoot so it can then approach the new direction more quickly than could be

achieved if it were designed not to overshoot—by, for example, having a highly

viscous damping system. Thus ﬁrst-order instruments are to be designed having a

time constant (lag) determined primarily by their size; a second-order instrument is

designed to have a time constant determined by its size but also a period of oscilla-

tion determined separately by the damping characteristics, which also are inﬂuenced

by size. The design must meanwhile ensure that any particular measurement

responds solely to the quantity of interest ; for example, rainfall should not inﬂuence

the measurement of air temperature. The science and art of instrument design

juggles these parameters to meet the needs of the way in which the data is to be used.

A further considerat ion lies in the spatial distribution of instruments and the

frequency at which observations are made. W hile economic considerations may

provide an upper boundary for the total number of instruments, the scale of the

phenomenon of interest and its velocity of propaga tion should determine the opti-

mum space distribution and frequency of measurement.

1 COMBINATION OF MEASUREMENTS

Many quantities of meteorological interest are to be derived by combination of

independent measurements from separate instruments (Stankov, 1998) of the same

region of interest or from regions which a re to be expected on physical grounds to be

highly cor related. Thus satellite measurements of ground emissivity at different

wavelengths over the same area should be comparable, as should radiative properties

of a given volume of particulates for identical viewing geometries. Under some

circumstances instruments combine to give ﬂuxes, as with a correlation between a

temperature ﬂuctuation (as measured by a thermocouple) and an air velocity ﬂuctua-

tion (as measured by a hot wire). Clearly the two instruments in the latter case are

never quite collocated, and problems arise from ﬂuctuations on the scale of the

differences of location. Yet further complications arise should different instruments

be of different order response (as with a wind vane and a thermocouple) and of

712 MEASUREMENT IN THE ATMOSPHERE

different time lags. The question arises concer ning the comparability of instruments

located at a ﬁeld site or on a moving platform as an aircraft. In the former case,

distances of order meters may be involved, to be combined with differences in local

airﬂow because of slightly different location geometry. In the case of aircraft,

competition for space may lead to quite different locations for different instruments.

Thus, air intakes for aerosol and gas measurements tend to be located at different

sites on the fuselage, whereas particle measurement probes tend to be located on

wing tip pylons; with different locations on the airplane, instruments are subject to

different airﬂow geometries.

For measurement of properties of rare particles, in concentrations occurring, say,

once per second in the sampling volume, it is clear that some hundred particles need

to be sampled—or some hundred seconds of data need to be collected to obtain

numbers meaningful, from a Poisson statistics viewpoint, at a 10% level. Thus a

scale of 10 km is a practical limit of resolution. Relating this to meaningful measure-

ments required to give insight into speciﬁc cloud processes—important, for example,

for aircraft icing or the structure of cirrus—may require measurements on a scale

well below 100 m (Liu et al., 2002). Hence the desig n of an instrument of adequate

volume sample, of adequate time response and, for derived quantities, of appropriate

collocation is no trivial undertaking. It is clear that instruments designed to measure

simultaneously several properties of a given air particle sample will give more

meaningful data to investigate the inhomogeneities shown by microwave studies

(Mace et al., 1998).

2 PARTICLE MEASUREMENT

Particles in the atmosphere range from the smallest of aerosol some tens of

nanometers in diameter in concentration in excess of 10

3

to large hailstones

of 10 cm in diameter, in concentration less than one per 10 m

. Such particles

comprise precipitation, cloud, and the atmospheric aerosol itself. Measureme nt

may characterize concentration, size distribution, and shape distribution. As an

example, we examine ice crystal characteristics—spectr a of habit, density, size,

and concentration necessary for derivation of radiative ﬂuxes in appropriate wave-

lengths and precipitation ﬂuxes under differing dynamical conditions. A ‘‘point’’

measurement is idealized, but it is clear that a sample time, which differs for different

size and other characteristics, needs to be speciﬁed. It is of interest to start with the

pioneering work of cirrus crystal forms carried out from an open cockpit using a

hand-held varnish-coated slide to give replicas for subsequent microscopic observa-

tion (Weickmann, 1947). This technique clearly showed the presence of three-

dimensional bullet rosettes. Yet even in this work it is clear that an assessment of

the relative occurrence of various crystal forms in the atmosphere—both as pristine

and as complex crystal shapes—is a major undertaking because of the intrinsic

variability of their nucleation and growth conditions. The early surface measure-

ments (Bentley and Humphries, 1962; Nakaya, 1954) tended to select ideal forms as

being of greater aesthetic value for sketching or photography, and later observations

2 PARTICLE MEASUREMENT 713

have similarly selected regions where crystal forms are relatively uniform. The

occurrence of multiple habits and multipeaked size spectra at a point measurement

is well documented in aircraft measurement and simplistically may be attributed

initially to different nucleation and growth processes (Korolev et al., 2000; Bailey

and Hallett, 2002), and subsequently to different fall speeds as well as the effects of

mixing in lateral shear as in Kelvin–Helmholtz instability at an inversion top.

A more fundamental question needing to be addressed is the meaning of any data

set of crystal shape, size, and habit distribution in a given measurement. The ques-

tion of time and spatial scale of the sample is of major importance, and the detail of

the averaging process is crucial as to how the data may be used. From a fundamental

viewpoint, we may be interested in the nucleation and growth processes in a given

volume of air that retains some coherence over growth times of interest—say some

hundreds of seconds , with some hope of characterizing individual crystals over such

a period. A Lagrangian observation strategy is therefore attractive, if not easily

accomplished. From an applied viewpoint, crystals need to be characterized over,

say, a volume of a lida r pulse some 1 m

; the volume of a radar pulse some 10

the volume of a satellite footprint some 100 km

. To assess precipitation from a

frontal system over its precipitation history, a volume of air some 10

is more

realistic; a precipitation of 1 cm over 1 km

requires some 10

individual crystals.

The realities of individual cr ystal measurement cannot compete, and the question of

what is necessary for a meaningful sample arises. Surface collection and microscopy

obviously gives a remarkably small sample and cannot provide a realistic sample for

such a use. Electro-optical systems (PMS 2DC; PMS 2DP) give greater ease of data

collection and are subject to some degree of automation, yet still provide a meager

sample in relation to the above numbers. A similar consideration applies to more

recent systems (Lawson et al., 1998). Some idea on variability in cirrus can be

obtained on a broad scale from microwave radar (Mace et al., 1998), and it is

clear that a cellular structure of order at least 100 m exists, as can readily be seen

from a cursory visual inspection of any ﬁeld of cirrus.

One may resort to a broader approach by assuming that in a sufﬁciently large

volume of space, particle concentration, or indeed any other characteristic results

from a combination of random events such that Shannon’s maximum entropy princi-

ple applies. In this case, a Weibull distribution results (Liu and Hallett, 1998), imply-

ing that any spectrum measurement is but one of a family, and a sufﬁcient data set may

be speciﬁed to provide the ‘‘best’’ (most probable) distribution. It is necessary to

specify a time or spatial boundary for such measurements; it may be convenient to

do this on physical grounds. For example, limiting time by a well-determined effect

(sea breeze=convection life time; Rossby wave transition time in Eulerian frame; a

ﬁeld of wave clouds, etc). Any individual measurement necess arily departs from this

ideal. The reality of any particle measurement lies in the statistics of the numbers in

each size bin. In general, there are fewer larger particles and an upper limit is set for

realism by Poisson statistics for the large, rare particles. Recall that radar scattering

relates to SNr

, mass vertical ﬂux to SNr

5,4,3.5

depending on fall regime, mass to

SNr

, optical effects to S Nr

, particle diffusion growth rate to SNr, and nucleation

processes to SN (S ¼ sum over all par ticles). Uncertainties arise in derived quantities

714 MEASUREMENT IN THE ATMOSPHERE

at different sizes depending where the size cut off in the measurements occurs for the

selected sampling time and spatial average. A further consideration lies in direct

measurement of properties of individual particles—such as impurity content and

mean density, or density related to radius. The cloudscope class of instruments is a

candidate for these measurements (Hallett et al., 1998).

From the viewpoint of an aircraft measurement, necessarily a long thin ribbon

along its ﬂight path, a longer path (space or time) to improve the statistics neces-

sarily implies the likelihood of leaving the area (also deﬁned in space or in time)

where particles are occurring—meters or some tens of kilometers at most (arguably)

for a cirrus regime or hundreds of kilometers for a ﬁeld of convective storms (Fig. 1).

Hence some formal deﬁnition of the spatial and volume scale and geometry of

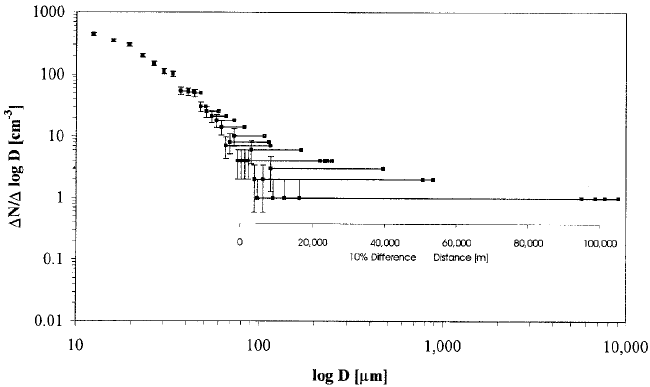
Figure 1 Analysis routine for an ice particle distribution collected by an airborne cloudscope

(an instrument which images particles collected on a forward facing optical ﬂat), sample

volume about 5 liters per second. The protocol is set initially by the selection of the number of

size bins on a logarithmic scale. It is further set by the level of uncertainty which can be

tolerated—for example 10%. The uncertainty in the number of particles actually counted in

each bin (N ) is given by Poisson statistics as N

1=2

, represented by the vertical error bars on

each point. The uncertainty is obviously large for the small concentrations of large par ticles.

The horizontal line from each point represents a ﬂight distance necessary to sample 100  10

particles (10% uncertainty) at the concentrations observed using the instrument of designated

sample volume. The physical domain over which any set of measurements must be analyzed is

then selectable. This could be (as this case) 10 km of a hurricane outﬂow for a speciﬁc size,

but would be something like 1000 km for marine stratus or the whole Northern Paciﬁc Ocean

for frontal systems for larger rarer particles. In order to reduce the sampling uncertainty, it

would be necessary to use an instrument with a greater sampling volume or sample for a

longer time=distance in regions of interest delineated by other considerations—for example

energy dissipation rate or radiance at a given wavelength. (Data collected on the NASA DC-8

in outﬂow of hurricane Earl approaching the Louisiana coast, September 2, 1998.)

2 PARTICLE MEASUREMENT 715