Poole Ch.P., Jr. Handbook of Superconductivity

Подождите немного. Документ загружается.

Chapter 4: Models and Theories

Fig. 4.1.

i%)12

3a.....~o

4b.

2b.

I,.12

\\\

(a)

-e-

I I I

0 I , I 1

0 1 2 3 4

x/P,

(b)

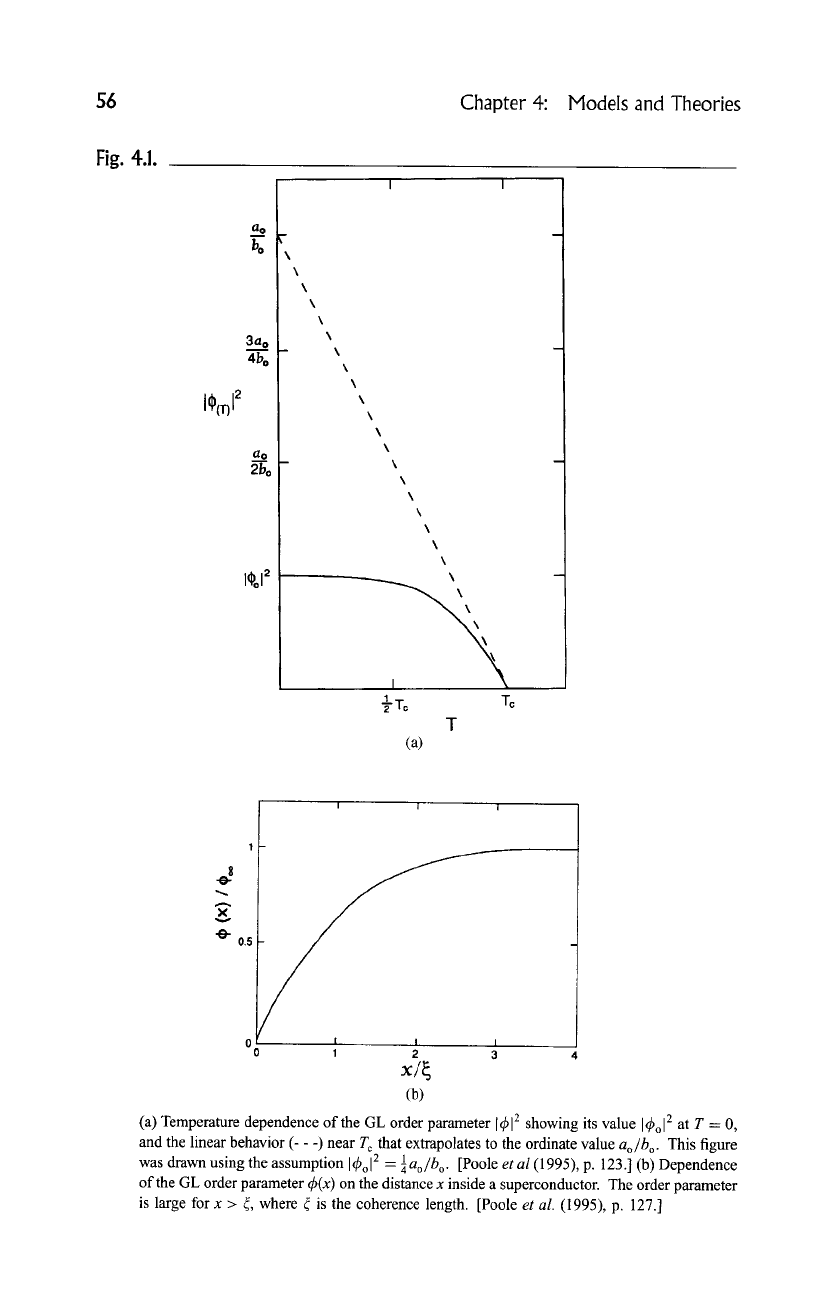
(a) Temperature dependence of the GL order parameter

I~l 2

showing its value 14~ol 2 at T = 0,

and the linear behavior (- - -) near T c that extrapolates to the ordinate value

ao/b o.

This figure

was drawn using the assumption 14~ol 2 =

88 o.

[Poole

et al

(1995), p. 123.] (b) Dependence

of the GL order parameter ~b(x) on the distance x inside a superconductor. The order parameter

is large for x > 4, where ~ is the coherence length. [Poole

et al.

(1995), p. 127.]

C. Ginzburg-Landau Theory 57

The condensation energy of the super electrons, the energy released per unit

volume by transforming normal electrons to the superconducting state, is given

gcond --

l (a2/b) -

B2/2#o .

(13)

In the presence of an applied magnetic field the line integral of J/l~l 2 around a

closed path inside the superconductor and the flux 9 enclosed by this path obey

the relation

(m* #o/e*2) ~

(,]/14)12) 9

+ 9 --

n(~ o ,

(14)

where n is an integer and the quantum of flux 9 o has the value

Oo-h/e*.

(15)

Equation (15) is the quantum condition whereby the sum of the enclosed flux 9

and the line integral of the current density J is quantized.

A parallel magnetic field

B(x)

and a current density

J(x)

decay exponen-

tially with the distance x inside the surface of a superconductor in accordance

with the expressions

B(x) - Bo e-x/~

(16a)

J(x) - Jc e-x/'z ,

(16b)

where the London penetration depth 2 L, the second fundamental length scale, is

given by

22 _ m*

#oe,2[qSoc [2,

(17)

in agreement with Eq. (3).

The ratio tc- 2/{ - 1/~/2 divides superconductors into the two types

1< < 1/x/2 (Type I) (1Sa)

t< > 1/x/2 (Type IX). (1Sb)

Type II superconductors have lower, thermodynamic, and upper critical fields

given by

9 o In ~c 9 o 9 o

Bcl =

-- ' Bc2 -- ~2' (19)

4Tc2 2 '

2V~rc~2 2re

respectively, where BclBc2-BZlnt<. The Meissner effect is complete for

Bap p

< Bcl ,

and

as Bap p

is increased above the low critical field Be1, flux

penetrates the material in the form of vortices. The magnetization continues to

increase until the upper critical field Bc2 is reached where the vortex cores almost

overlap and bulk superconductivity is destroyed. Residual superconductivity may

58 Chapter

Models and Theories

persist in a thin sheath up to an even higher critical field Bc3 - x/~Bc2 where the

entire sample goes completely normal.

Bardeen-Cooper-Sch rieffer Theory

In 1957 Bardeen, Cooper, and Schrieffer (BCS) proposed the general microscopic

theory of superconductivity that quantitatively predicts many properties of

superconductors and is now widely accepted as providing a satisfactory explana-

tion of the phenomenon. There are various levels of approximation in which the

BCS theory has been applied, and some of them are commented upon in the next

section. The mathematical underpinning of the BCS theory is so complex that it

will not be of much benefit to summarize its general formulation, so this section

will emphasize predictions that are often compared with experiment. These

predictions arise mainly from the homogeneous, isotropic, phonon-mediated,

square well, s-wave coupling simplification of the BCS theory, and many

superconductors, to a greater or lesser extent, have been found to satisfy these

predictions. Some of them are as follows:

The isotope effect involves the claim that for a particular element the

transition temperature T c depends on the mass M of the isotope as follows:

M~Tc -

const. (20)

The weak coupling BCS limit [vide Eqs. (24) to (26)] gives the value ~ ~ 1/2,

which has been observed in some superconducting elements, but not in all of

them.

A superconductor has an energy gap Eg -- 2A(k), which is assumed to be

independent of k, and for this assumption the energies in the normal and

superconducting states are

g(~)- (~2 _]_ A2)1/2

(normal state)

, (21)

(superconducting state)

where { is the energy in the absence of a gap measured relative to the chemical

potential #:

h2k 2

= ~- #. (22)

D. Bardeen-Cooper-Schrieffer Theory 59

The density of states

D(E)

given by (with E - 0 at the center of the gap)

Dn(O)E

( E2

A2)1/2 , E > A

Ds(E)- 0, -A < E < A

-Dn(O)E

( E2

A2)1/2 , E < -A

(23)

is shown plotted in Fig. 2.7, where the normal electron density of states Dn(E ) is

assumed to have the constant value Dn(0 ) in the neighborhood of the gap.

Consider a square-well electron-electron potential V o and an energy gap

A(k) that is equal to A o in the neighborhood of the Fermi surface,

A(k) = A o, -ho9 D _< ~(k) < hOgD, (24)

and is zero elsewhere. The Debye frequency o.) D determines the range of

because it is assumed that Cooper pair formation is mediated by phonons. The

energy gap A o in this approximation is given by

])(D D

A o = . (25)

sinh[1/VoDn(O)]

In the weak coupling (small Vo) limit,

VoDn(0 ) << 1,

kBT c

((ho) D. (26)

we obtain the dimensionless ratios

Eg = 2A o _-- 2__~ ---- 3.52, (27)

kB T c kB T c e~

where 7 - 0.5772... is the Euler-Mascheroni constant. This ratio approximates

experimental measurements that have been made on many superconductors.

The dimensionless electron-phonon coupling constant 2 is related to the

phonon density of states Dph(O9 ) through the Eliashberg expression:

2 - 2-(~2(og)Dph(O))

do9.

(28)

(_o

Superconductors are characterized as having weak (2 << 1), intermediate (2 ~ 1),

and strong (2 >> 1) coupling. The electron-electron interaction potential V o for

Cooper pair bonding has an attractive electron-phonon part measured by 2 and a

repulsive screened Coulomb part #~ to give

VoDn(0 ) - 2 - kt c , (29)

and this provides the following approximate expression for the transition

temperature:

T c - 1.13 0 D exp[- 1/(2

-/~*)].

(30)

Chapter

Models and Theories

A number of related formulas for the dependence of Tc on 2 and #* have

appeared in the literature (e.g., McMillan, 1968).

The BCS theory predicts that at T~ there is a jump in the electronic specific

heat from its normal state value Ce = 7T to its superconducting state value C s

given by

Cs -TT~

= 1.43. (31)

In the free electron approximation the electronic specific heat coefficient 7

depends on the Fermi temperature T F and the gas constant R through the

expression

-- ~z2R/2TF .

(32)

Below To, the BCS theory predicts that the specific heat Cs(T ) depends

exponentially on the inverse temperature,

Cs(T )

-- a exp[-A/kBT ],

(33)

where A - 1.76 k B T c, and a is a constant.

Mechanisms for Cooper Pairing

There are three levels of explanation of the nature of superconductivity that are

commonly called BCS. One is the general formulation that does not specify

particular interactions. The second is the phonon-mediated version of the theory,

in which phonons play the role of bringing about the coupling together of two

electrons to form Cooper pairs. The third level, which was described in the

original formulation of the theory and provided the results summarized in the

previous section, further assumes the simplification of an isotropic, homogeneous

material with a square-well electron-electron interaction potential involving a

phonon coupling mechanism and s-wave singlet-state pairing. The superconduct-

ing elements, which are almost all Type I, as well as many classical Type II

superconductors, are looked upon as phonon-mediated s-state types. Pairing

mechanisms involving the exchange of particles other than phonons, such as

excitons or antiferromagnetic spin fluctuations, have been proposed for non-

classical superconductors. In particular, no consensus exists yet about the pairing

mechanism of the cuprates, although d-wave pairing seems to be favored (Annett

et al., 1996). A handbook is probably not the appropriate forum for elaborating

on these matters.

E Critical State Models 61

Critical State Models

A critical state model postulates that for low applied fields or currents the outer

part of the sample is in what is called a critical state, with particular values of

current density and magnetic field, and that the interior is shielded from these

fields and currents. The magnetic field B and the super current density J are

coupled through the Maxwell relation

V x B = #o J, (34)

which has the following form in the one-dimensional cases to be discussed here:

dx Bz(x) - #oJy(x),

(35)

and each model makes an assumption about the magnetic field dependence

J(B)

consistent with these Maxwell relations. Fields and currents applied simulta-

neously and then reversed in direction produce modified critical states in the outer

parts of the sample. High values of the applied field or currents extend the critical

state to fill the entire superconductor. The models do not take into account the

existence of a lower critical field Bcl, or the difference between the Meissner and

the mixed states. They do not explain the nature of superconductivity, but rather

provide a convenient description of some experimentally observed phenomena.

Many configurations

ofBz(x )

and

Jy(x)

meet requirement (35), and for most

models the critical state current density is related to the field by a characteristic

equation,

Jy(Bz) = JK/f (Bz),

(36)

where ark is independent of the field and is generally the critical current Jc. The

characteristic equations of nine critical state models are provided elsewhere

(Poole

et al,

1995). By far the most widely used of these models is the Bean

model (Bean, 1962, 1964), which has the simplest characteristic equation:

J(B)

=Jc. (37)

The Kim model (Kim

et al,

1962, 1963) has also been used occasionally, and it

makes the assumption

J(B) = . (38)

1 + IB(x)I/BK

Perhaps the most important application of the Bean model is the determination of

the critical current density Jc from magnetic hysteresis loops.

62 Chapter 4: Models and Theories

Bean Model

The Bean model assumes that the current density can only take on the values :EJ c

or 0. A sample of thickness 2a has a characteristic field B*,

B* - #oJc a,

(39)

and when the applied field B o attains this value B*, the fields and currents reach

the center of the sample. We shall examine the one-dimensional case (35) for

applied fields below and above B*.

For low applied fields, B o < B*, the internal fields and currents only exist

near the surface, with a field and current-free region (-a' < x < a') near the

center, and the current density given by, from Eq. (37),

Jy(x)- Jc, -a < x < -a'

Jy(x)- O, -a' < x <_ a'

Jy(x) - -Jc, a' <_ x < a.

(40)

These formulas match the boundary condition

Bz(O ) - B o

at the surfaces x - +a,

with the magnitudes ofJ c and B o related by the expression obtained from Eq. (35)

B o

Jc - #o(a _ a')" (42)

These expressions for

Bz(x )

and

Jy(x)

are plotted in Fig 4.2a for a finite value of

a', and in Fig. 4.2b for the case where B o - B* and a' - 0.

For high applied fields, B o > B*, the currents and intemal fields are present

throughout the sample and are given by the expressions

Jy(x)- Jc, -a < x < 0

Jy(x)- -Jc, 0 <_ x <_ a

(43)

Bz(x ) Bo _ B,[a + x]

- , -a<_x<_O

Bz(x )_ Bo + B*[X- a],

0<x<_ _ a.

(44)

Equation (35) requires that

Bz(x )

depend linearly on x in the regions where

- ~-Jc, so we have for the internal magnetic fields

[a,+x]

Bz(x) - B~ a' - ' -a _ < x _ < -a

Bz(x ) -- O, -a' <_ x < a'

(41)

[x a]

Bz(x)--B o a' < x < a.

a t , _ _

G. Bean Model 63

Fig. 4.2.

(a)

Bz(x)

I ,,

-a

(b)

-a 0 a

(c)

2B*

-a" () a

Jy(X)

-a

-Jc

-a

-Jo

'-a

-Jc

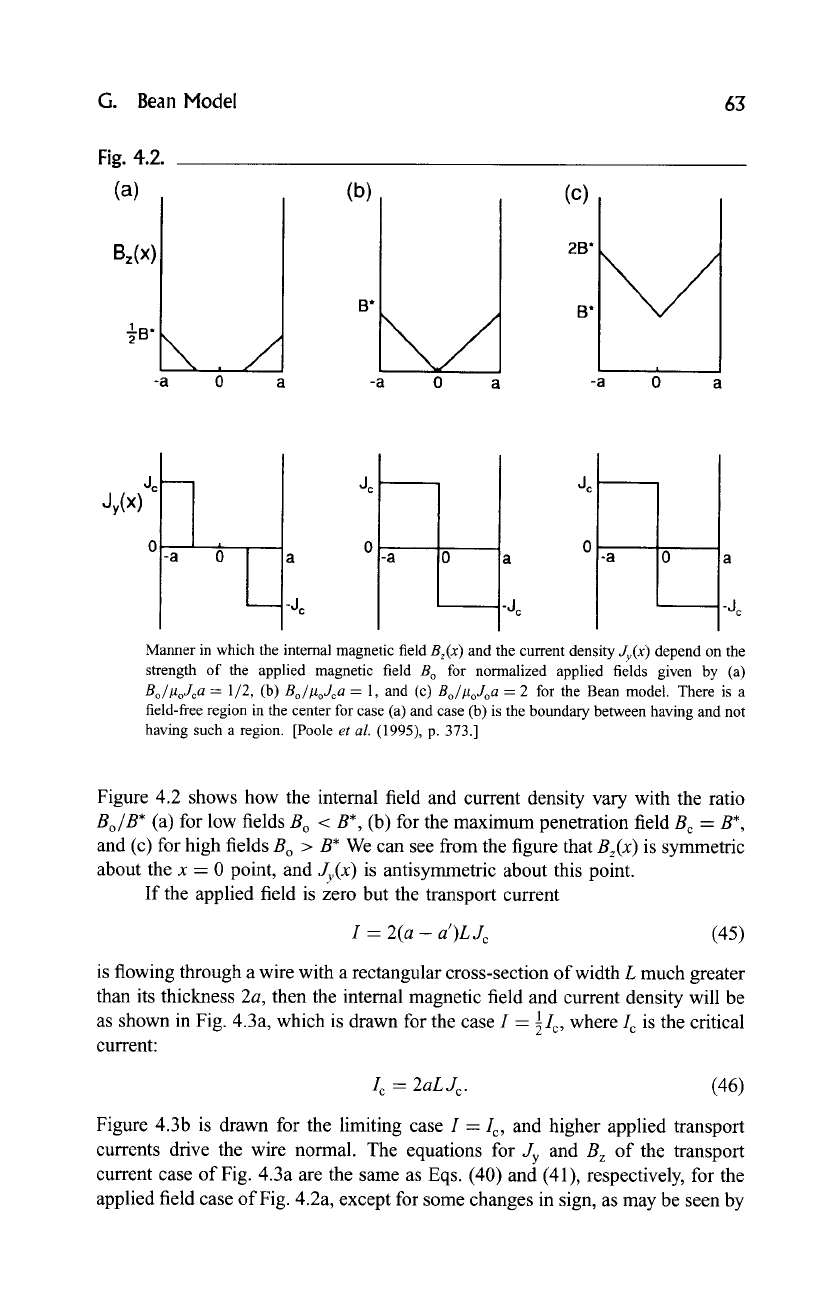
Manner in which the internal magnetic field

Bz(x )

and the current density

Jy(x)

depend on the

strength of the applied magnetic field B o for normalized applied fields given by (a)

Bo/l~oJca

= 1/2, (b)

Bo/#oJca

= 1, and (c)

Bo/#oJoa

= 2 for the Bean model. There is a

field-free region in the center for case (a) and case (b) is the boundary between having and not

having such a region. [Poole

et al.

(1995), p. 373.]

Figure 4.2 shows how the internal field and current density vary with the ratio

Bo/B*

(a) for low fields B o < B*, (b) for the maximum penetration field B c = B*,

and (c) for high fields B o > B* We can see from the figure that

Bz(x )

is symmetric

about the x = 0 point, and

Jy(x)

is antisymmetric about this point.

If the applied field is zero but the transport current

I - 2(a -

a')LJ c

(45)

is flowing through a wire with a rectangular cross-section of width L much greater

than its thickness 2a, then the internal magnetic field and current density will be

as shown in Fig. 4.3a, which is drawn for the case I - !/. where I c is the critical

2 c,

current:

I c - 2aLJ c.

(46)

Figure 4.3b is drawn for the limiting case I- I c, and higher applied transport

currents drive the wire normal. The equations for Jy and B z of the transport

current case of Fig. 4.3a are the same as Eqs. (40) and (41), respectively, for the

applied field case of Fig. 4.2a, except for some changes in sign, as may be seen by

64 Chapter 4: Models and Theories

Fig. 4.3.

(a)

8,(x) J

(b)

" B"

Jy(x)

.... i

-a ~ a -a 0 a

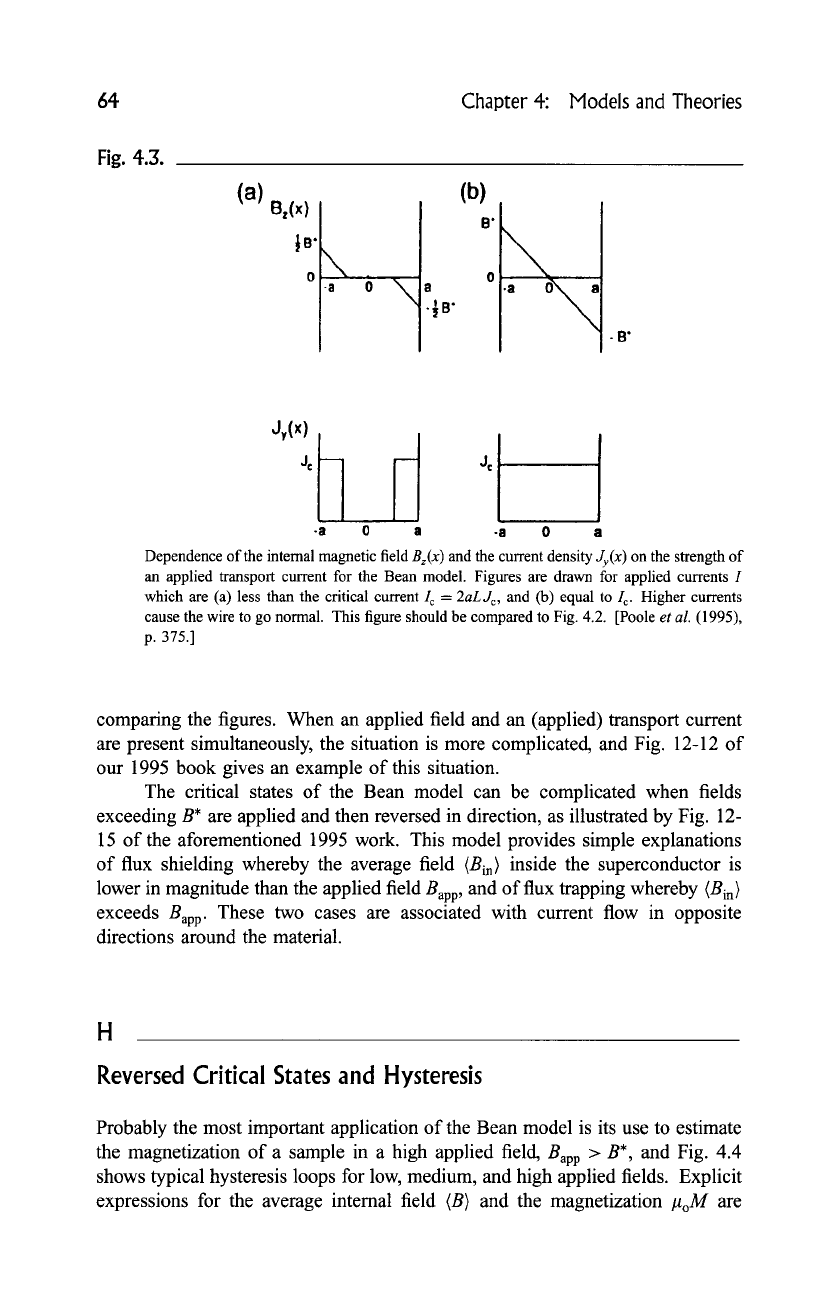
Dependence of the internal magnetic field

Bz(x )

and the current density @(x) on the strength of

an applied transport current for the Bean model. Figures are drawn for applied currents I

which are (a) less than the critical current I c =

2aLJc,

and (b) equal to I c. Higher currents

cause the wire to go normal. This figure should be compared to Fig. 4.2. [Poole

et al.

(1995),

p. 375.]

comparing the figures. When an applied field and an (applied) transport current

are present simultaneously, the situation is more complicated, and Fig. 12-12 of

our 1995 book gives an example of this situation.

The critical states of the Bean model can be complicated when fields

exceeding B* are applied and then reversed in direction, as illustrated by Fig. 12-

15 of the aforementioned 1995 work. This model provides simple explanations

of flux shielding whereby the average field

(Bin)

inside the superconductor is

lower in magnitude than the applied field

Bapp,

and of flux trapping whereby

(Bin)

exceeds Bap p. These two cases are associated with current flow in opposite

directions around the material.

Reversed Critical States and Hysteresis

Probably the most important application of the Bean model is its use to estimate

the magnetization of a sample in a high applied field, Bap p > B*, and Fig. 4.4

shows typical hysteresis loops for low, medium, and high applied fields. Explicit

expressions for the average internal field (B) and the magnetization po M are

Fig. 4.4.

(a)

(b)

-1

a' 89

b o

, I

.89 Ba~ / B*

(c)

}.tom

-2

Bap p / B*

al A , ,, , ~

- -1

H. Reversed Critical States and Hysteresis 65

B o = 3B* ]

; ~ BapP/B*

1 2 b"~

,~.~ a

......

Hysteresis loops of magnetization/toM vs the applied magnetic field Bap p cycled over the range

-B o < Bap p _< B o for the three cases (a) B o =

89

(b) B o = (5/4)B*, and (c) B o = 3B*.

[Poole

et al.

(1995), p. 388.]

given in Table 12-2 of our earlier work (1995) for the special points a, b, c, d, and

e of these loops. A high field hystereisis loop (B o > B*) furnishes the difference

M+ - M_ - Jca

(47)

between the upper and lower magnetization plateaus of Fig. 4.4c, where

oi+

#oM_ _ _ 1 B*,

(48)