Поляк Б.Т., Щербаков П.С. Робастная устойчивость и управление
Подождите немного. Документ загружается.


1.2. Передаточная функция 21
номер итерации в итерационном процессе или время может быть дискретным в процес-
сах, связанных с цифровым управлением. Открытая дискретная система приобретет
вид
x
k
= Ax
k−1
+ D
1
w
k−1
,
y
k
= Cx
k
+ D
2
w
k
,
(1.5)
а ее решение также выписывается в явной форме:
x
k
= A
k
x
0
+
k−1
X
i=0
A
k−i−1
D
1
w
i
. (1.6)
Сопутствующие функции Matlab:
ss (CST) — задание системы в пространстве состояний и переход от других описаний
(см. ниже) к пространству состояний;
ss2ss (CST) — переход к другим координатам при описании в пространстве состояний;
ssdata (CST) — извлечение данных (вычисление матриц системы) с предварительным
преобразованием (если необходимо) к пространству состояний;
c2d (CST) — дискретизация непрерывной системы;
expm — матричная экспонента;
funm — вычисление функции общего вида от матрицы.
1.2 Передаточная функция
Проведем некоторые формальные преобразования уравнений в пространстве состо-
яний. Введем оператор дифференцирования по времени: s =
d
dt
; на гладкие функции
x(t) он действует по правилу
sx(t) = ˙x(t). (1.7)
Будем относиться к s как к комплексной переменной и рассматривать различные функ-
ции от нее; им нетрудно придать содержательный смысл. Например, если
R(s) = a
0
+ a
1
s + . . . + a
k
s
k
,
то
R(s)x(t) = a
0
x(t) + a
1
˙x(t) + . . . + a
k
x
(k)
(t).
Тогда, подставив s
.
=
d
dt
в (1.1) (при x(0) = 0) и формально разрешая первое уравнение
относительно x, получим
x = (sI − A)
−1
(Bu + D
1
w),
и для выхода получаем выражение
y = C(sI − A)
−1
Bu +
h
C(sI − A)
−1
D
1
+ D
2
i
w. (1.8)

22 Глава 1. Описание линейных систем
Матричная функция комплексного переменного s
H
yu
(s)
.
= C(sI − A)
−1
B
называется передаточной функцией от управления u к выходу y, а аналогичная функ-
ция
H
yw
(s)
.
= C(sI − A)
−1
D
1
+ D
2
называется передаточной функцией от возмущения w к выходу y.
Рассмотрим эти функции подробнее. Элементами матриц H(s) являются дробно-
рациональные функции от переменной s, которые имеют общий знаменатель
P (s)
.
= det(sI −A) (1.9)
— характеристический полином матрицы A. Этот полином от переменной s будем назы-
вать характеристическим полиномом системы, так как в дальнейшем увидим, что от
расположения его корней зависят такие важные свойства системы как устойчивость и
другие. С учетом обозначения (1.9) H
yu
(s) (и, аналогично, H
yw
(s)) представима в виде
H
yu
(s)
.
= H(s) =
1
P (s)
W (s), (1.10)
где W (s) — матрица, элементы которой — полиномы от s. Действительно, для любой
невырожденной матрицы M ∈ R
n×n
M
−1
=
1
det M
c
M,
где
c
M = ((
c
m
ij
)) — матрица, состоящая из алгебраических дополнений (присоединенная
матрица):
c
m
ij
= (−1)
i+j
det M
ji
;
здесь M
ji
— матрицы, получающиеся из M вычеркиванием j-й строки и i-го столбца.
Поэтому, если M = (sI −A), то
c
m
ij
— полиномы от s, откуда и следует выражение (1.10).
Нули s
i
характеристического полинома P (s) называются полюсами передаточной
функции H(s):
s
i
: P (s
i
) = 0, i = 1, . . . , n.
Таким образом, полюса H(s) совпадают с собственными числами матрицы A; для всех
остальных s матрица H(s) определена. В частности, если P (s) устойчив (см. ниже,
Гл. 3), т.е. все его корни лежат в открытой левой полуплоскости, то H(s) — матричная
функция, аналитичная в правой полуплоскости. Мы будем неоднократно пользоваться
этим в дальнейшем, и такие передаточные функции называем устойчивыми.
Возвращаясь к (1.8), на языке передаточных функций выход системы как функцию
от управления и внешних входов можем записать в следующем виде:
y = H
yu
(s)u + H
yw
(s)w. (1.11)
Строгое обоснование перехода от записи (1.1) системы в пространстве состояний к
форме (1.11) может быть сделано с помощью преобразования Лапласа; мы сейчас не

1.2. Передаточная функция 23
будем этим заниматься, а будем рассматривать (1.11) просто как иную форму записи
дифференциальных уравнений (1.1).
Разумеется, описание (1.11) системы с помощью передаточных функций может быть
и исходным; иногда оно возникает более естественно, чем описание в пространстве со-
стояний. Рассмотрим для простоты ситуацию, когда внешние возмущения и ошибки
измерения выхода отсутствуют:
y = H(s)u, u ∈ R
m
, y ∈ R
l
. (1.12)
В этой записи под передаточной функцией H(s) будем понимать матрицу l × m, эле-
менты которой есть дробно-рациональные функции от s, т.е. H(s) представима в виде
H(s) =
1
P (s)
W (s), (1.13)
где элементы l ×m матрицы W (s) являются полиномами от s. Полином P (s) — общий
знаменатель элементов матрицы H(s) — будем называть характеристическим поли-
номом системы, а его корни — полюсами передаточной функции (системы). Такое
определение характеристического полинома и полюсов системы не вполне точно, по-
скольку могут возникнуть неприятности, связанные, например, с возможным сокраще-
нием неустойчивых полюсов (см. обсуждение в разделе 3.4). Более строгое определение
дается следующим образом.
Формально умножив обе части (1.12) на P (s), с учетом (1.13) получим
P (s)y = W (s)u, (1.14)
и, рассматривая теперь s как оператор дифференцирования, приходим к системе диф-
ференциальных уравнений высокого порядка относительно y(t) ∈ R
l
, u(t) ∈ R
m
. На
элементы матрицы H(s) естественно накладывать дополнительное условие реализуе-
мости: степень полинома в числителе не превосходит степени полинома в знаменателе
(см. также ниже, раздел 1.4); такие передаточные функции будем называть правильны-
ми или реализуемыми. Тогда, вводя “искусственные” переменные — состояния — можно
привести уравнение (1.14) к виду, аналогичному (1.1). Иными словами, от записи систе-
мы с помощью реализуемой передаточной функции можно перейти к эквивалентному
описанию в пространстве состояний, которое принято называть реализацией передаточ-
ной функции в пространстве состояний. При этом используют запись
H(s) =
"
A B
C D
#
(1.15)
или H(s) = (A, B, C, D), которые означают, что система y = H(s)u эквивалентна систе-
ме
˙x = Ax + Bu, x(0) = 0,
y = Cx + Du,
и при этом
H(s) = C(sI − A)
−1
B + D.

24 Глава 1. Описание линейных систем
Переход от H(s) к (A, B, C, D)-реализации может быть осуществлен различными спо-
собами, и таких реализаций много. Среди них существуют такие, в которых размер-
ность A (т.е. размерность вектора состояний x) минимальна; они называются мини-
мальными реализациями. Соответствующая размерность A называется степенью Мак-
Миллана для передаточной функции. Эта степень может быть найдена с помощью спе-
циального алгоритма — приведения H(s) к так называемой форме Мак-Миллана. Если
(A, B, C, D) — минимальная реализация H(s), то
P (s)
.
= det(sI −A)
представляет собой характеристический полином системы, а его корни — собственные
значения A — называются полюсами матричной передаточной функции (полюсами
системы).
В дальнейшем мы увидим, что запись с помощью передаточных функций чрезвы-
чайно удобна; сейчас проиллюстрируем это на простом примере. Пусть имеется несколь-
ко объектов соответствующих размерностей, соединенных последовательно, так что вы-
ход y
k
каждого служит входом u
k+1
последующего (рис. 1.1), причем каждый объект
имеет свою передаточную функцию H
k
(s):
y
k
= H
k
(s)u
k
, k = 1, . . . , m;
мы для простоты полагаем, что имеется единственный входной сигнал u, а ошибки
измерения v отсутствуют.
-
u = u
1
H
1
(s)
-
y
1
= u
2
H
2
(s)
-
y
2
= u
3
. . .
-
y
m−1
= u
m
H
m
(s)
-
y
m
= y
Рис. 1.1: Последовательное соединение объектов.
Подставляя последовательно, получаем для связи общего входа u = u
1
и выхода
y = y
m
:
y = y
m
= H
m
(s) ···H
1
(s)u
1
= H(s)u,
т.е. передаточная функция последовательного соединения равна произведению переда-
точных функций объектов:
H(s) = H
m
(s) ···H
1
(s). (1.16)
Выразить такое соотношение на языке пространства состояний было бы гораздо
труднее. Поэтому в инженерной практике, где нередко рассматриваются сложные со-
единения простых звеньев (блок-схемы системы), язык передаточных функций явля-
ется общепринятым. При этом существуют простые правила, позволяющие рассчитать
итоговую передаточную функцию блок-схемы по передаточным функциям звеньев (по-
добные правилу (1.16) для последовательного соединения).
Обсудим еще одно важное свойство передаточных функций, поясняющее удобство
такого способа описания систем. Предположим, что система (1.1) имеет вид
˙x = Ax + Bu,
y = Cx,
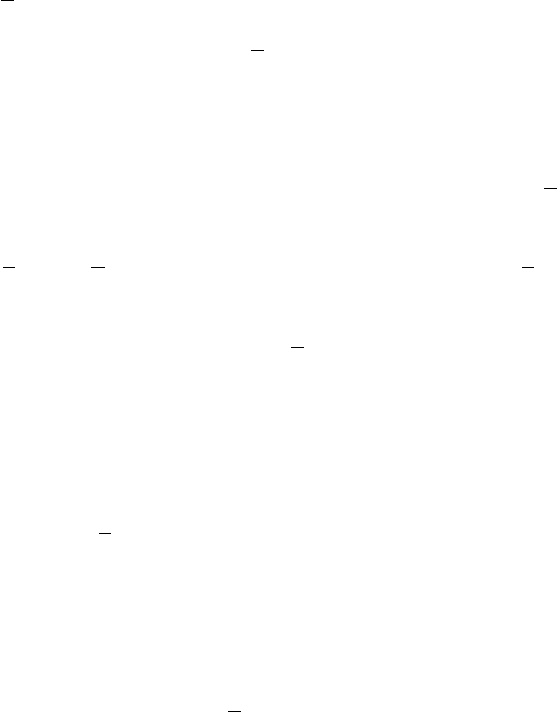
1.2. Передаточная функция 25
а входное воздействие u(t) — комплексный гармонический сигнал:
u(t) = ae
jωt
,
где a — некоторый постоянный вектор, а ω — частота колебаний (напомним, что в
теории управления мнимую единицу принято обозначать j, а не i, как обычно в мате-
матике). Из формулы (1.3) для решения системы x(t) получим
x(t) = e
At
x(0) + e
At
t
Z
0
e
(jωI−A)τ
Badτ
= e
At
x(0) + (jωI − A)
−1
Bae
jωt
− (jωI − A)
−1
e
At
Ba, (1.17)
и через x(t) обозначим установившееся значение вектора состояния
x(t)
.
= (jωI − A)
−1
Bu(t). (1.18)
Предположим, что матрица A устойчива, т.е. все ее собственные значения λ
i
лежат в
левой полуплоскости: Re λ
i
< 0, i = 1, . . . , n (подробнее вопрос об устойчивых матрицах
и системах обсуждается ниже, в Главе 3). Можно показать, что для устойчивых матриц
e
At
→ 0 при t → ∞. Тогда из (1.17)–(1.18) следует |x(t) − x(t)| → 0 при t → ∞. Таким
образом, для установившегося значения выхода имеем
y(t)
.
= Cx(t) = C(jωI − A)
−1
Bu(t), |y(t) − y(t)| → 0 при t → ∞,
или, иначе говоря,
y(t) = H(jω)u(t), (1.19)
где матричная функция H(jω) называется частотной характеристикой системы.
Поясним смысл полученного соотношения (1.19). Пусть все компоненты входного
вектора u(t) равны нулю, кроме i-й, которую представим в виде u
i
(t) = a cos ωt+ja sin ωt
(где a — число). Тогда k-я компонента установившегося значения выходного сигнала
равна
y
k
(t) = |h
ki
(jω)|a cos(ωt + ϕ) + j|h
ki
(jω)|a sin(ωt + ϕ),
где h
ki
(jω) — (k, i)-й элемент матрицы H(jω), а ϕ = arg h
ki
(jω). В силу линейности
H(·) отклик системы на сумму вещественной и мнимой составляющих u(t) равен сумме
откликов на каждую из них, т.е. если в качестве u
i
(t) взять вещественную гармонику
a cos ωt, то установившееся значение на k-м выходе будет
y
k
(t) = |h
ki
(jω)|a cos(ωt + ϕ).
Приходим к важному выводу: если на i-й вход системы с устойчивой матрицей A
подается гармонический сигнал с частотой ω, то на k-м выходе в пределе получается
также гармонический сигнал с той же частотой. Его амплитуда в |h
ki
(jω)| раз отлича-
ется от амплитуды входного сигнала (т.е. |h
ki
(jω)| имеет смысл коэффициента усиле-
ния входного гармонического сигнала), а фаза изменяется на arg h
ki
(jω). Это свойство
используется на практике для определения частотной характеристики системы экспе-
риментальным путем.

26 Глава 1. Описание линейных систем
Таким образом, в терминах передаточных функций очень удобно описывать транс-
формацию гармонических сигналов, проходящих через линейную систему.
Введем теперь передаточные функции для дискретных систем. Определим оператор
сдвига назад z:
zx
k
= x
k−1
, (1.20)
и аналогично непрерывному случаю будем рассматривать его как формальную пере-
менную. Тогда при x
0
= 0 уравнение (1.4) запишется в форме
x
k
= zAx
k
+ zBu
k
+ zD
1
w
k
,
т.е.
x
k
= z(I − zA)
−1
Bu
k
+ z(I − zA)
−1
D
1
w
k
,
y
k
= zC(I − zA)
−1
Bu
k
+
h
zC(I − zA)
−1
D
1
+ D
2
i
w
k
.
Передаточные функции теперь выражаются через переменную z по формулам
H
yu
(z) = zC(I − zA)
−1
B, H
yw
(z) = zC(I − zA)
−1
D
1
+ D
2
, (1.21)
и характеристическим полиномом системы так же, как и раньше, будем называть
общий знаменатель элементов матричных передаточных функций, т.е. полином
P (z)
.
= det(I −zA)
от переменной z. Соответственно, передаточные функции (1.21), как и в непрерывном
случае, имеют вид
H(z) =
1
P (z)
W (z),
где W (z) — матрица, элементы которой являются полиномами от z. Поэтому, если P (z)
не имеет нулей внутри единичного круга, т.е. является устойчивым по Шуру
1
(экви-
валентно, матрица A дискретно устойчива, т.е. |λ
i
| < 1 для всех собственных значе-
ний A), то H(z) аналитична в этом круге.
Аналогично тому, как это сделано для непрерывных систем, можно показать что
если у открытой системы (1.5) без ошибок в наблюдении выхода (D
2
= 0) матрица A
дискретно устойчива, а на вход подается гармонический сигнал
u
k
= ae
jωk
,
то выход стремится к установившемуся значению, записываемому формулой
y
k
= H(e
−jω
)u
k
, H(e
jω
)
.
= e
jω
C(I − e
jω
A)
−1
B,
т.е. и в этом случае гармонические сигналы преобразуются в пределе в гармонические,
с амплитудой, измененной в |H(e
jω
)| раз и сдвигом по фазе, равным −arg H(e
jω
) (знак
“−” соответствует оператору z сдвига назад).
1
Вопросы дискретной устойчивости полиномов и матриц подробно рассматриваются в разделах 3.2,
3.3.3 и 4.1.3.
1.3. Операторный подход 27
Мы вновь видим, что язык передаточных функций хорошо приспособлен к описа-
нию прохождения гармонических сигналов, имеющих фиксированную частоту. Поэтому
методы, основанные на таком подходе, обычно называют частотными.
Сопутствующие функции Matlab:
tf (CST) — задание системы с помощью передаточных функций и переход от других
форм записи к передаточной функции;
tfdata (CST) — извлечение данных (числителя и знаменателя передаточной функции)
с предварительным преобразованием (если необходимо) к частотной форме;
pole (CST) — вычисление полюсов системы;
append, connect, feedback, parallel, series (CST) — различные соединения зве-
ньев, заданных как передаточной функцией, так и в пространстве состояний;
freqresp (CST) — вычисление частотной характеристики;
minreal (CST) — построение минимальной реализации передаточной функции;
poly — вычисление характеристического полинома матрицы;
det — вычисление определителя матрицы;
inv — обращение матрицы.
1.3 Операторный подход
В последние годы все большее распространение получает еще один способ описа-
ния линейных систем, опирающийся на язык функционального анализа. Рассмотрим
непрерывную открытую систему
˙x = Ax + Bu, x(0) = 0,
y = Cx
(1.22)
при нулевых начальных условиях и отсутствии ошибок на выходе w = 0. Тогда сигнал
на выходе (y) линейно зависит от сигнала на входе (u):
y = Lu, (1.23)
где L — некоторый линейный оператор, действующий в соответствующих простран-
ствах функций. В данном случае, в соответствии с формулой (1.3), этот оператор яв-
ляется линейным интегральным оператором и имеет явное выражение
y(t) =
t
Z
0
Ce
A(t−τ)
Bu(τ)dτ
.
=
t
Z
0
h(t − τ )u(τ)dτ; (1.24)
28 Глава 1. Описание линейных систем
функция h(t) называется (матричной) весовой функцией системы, см. ниже, в разде-
ле 1.4. Однако можно рассматривать и более общие линейные операторы L (1.23), за-
дающие соответствие входа и выхода; при этом система не обязательно приводима к
виду (1.22). На такие операторы следует наложить естественные ограничения, напри-
мер, требование причинности: значение выхода y(t) в момент t не может зависеть от
значений входа u(τ) в будущем, при τ > t. Очень важно также, чтобы оператор L был
oграниченным. Чтобы строго определить это понятие, нам нужно ввести функциональ-
ные пространства, в которых определены сигналы, и нормы в них.
1.3.1 Нормы сигналов
Будем считать, что все сигналы определены на полуоси 0 ≤ t < ∞. Основные про-
странства, с которыми придется иметь дело, это
1) L
2
— пространство ограниченных с квадратом функций, в котором рассматри-
ваются измеримые функции u(t), заданные на 0 ≤ t < ∞ и имеющие ограниченную
2-норму:
kuk
2
.
=
∞
Z
0
|u(t)|
2
2
dt
1/2
< ∞. (1.25)
Здесь |u(t)|
2
— евклидова норма вектора u(t) ∈ R
m
. Во многих физических приложениях
ku(t)k
2
2
означает энергию сигнала, поэтому L
2
— пространство сигналов ограниченной
энергии. Отметим, что если u ∈ L
2
, то из конечности интеграла в (1.25) следует u(t) → 0
при t → ∞. Поэтому, например функция u(t) ≡ 1 не принадлежит L
2
, равно как и
функция u(t) = sin ωt при любом ω 6= 0.
2) L
∞
— пространство существенно ограниченных функций. В него входят изме-
римые функции u(t) с ограниченной ∞-нормой:
kuk
∞
.
= sup
0≤t<∞
|u(t)| < ∞,
где |u(t)| — какая-нибудь векторная норма в R
m
(как правило, это ∞- или 2-норма).
Заметим, что более правильно было бы писать
kuk
∞
= ess sup
0≤t<∞
|u(t)|,
где ess sup — существенная верхняя грань функции, получающаяся при пренебреже-
нии множествами нулевой меры. Мы, однако, будем считать, что функция u(t) уже
изменена на множестве нулевой меры так, что величина sup |u(t)| оказалась минималь-
ной. Например, вместо u(t) = 0, t 6= 1, u(1) = 1, мы рассматриваем эквивалентную ей
u(t) ≡ 0; для обеих функций kuk
∞
= 0.
Обычно kuk
∞
измеряет интенсивность сигнала, так что L
∞
— пространство сигна-
лов ограниченной интенсивности. Функции u( t) ≡ 1 и u(t) = sin ωt принадлежат L
∞
,
однако
u(t) =
(
1/t
α
0 ≤ t ≤ 1
0 t > 1
, 0 < α < 1/2
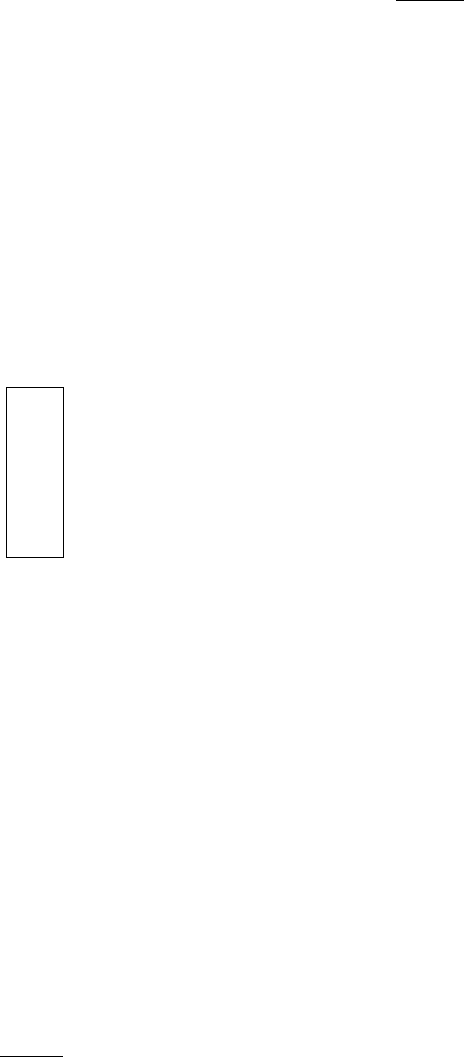
1.3. Операторный подход 29
не принадлежит L
∞
(она не ограничена), но принадлежит L
2
(ku(t)k
2
= 1/
√
1 − 2α).
3) L
1
— пространство абсолютно интегрируемых функций, для которых ограниче-
на 1-норма:
kuk
1
.
=
∞
Z
0
|u(t)|dt < ∞,
где также |u(t)| — норма вектора u(t) ∈ R
m
(как правило, 1-норма). Функция
u(t) =
(
1/t
α
0 ≤ t ≤ 1
0 t > 1
, 1/2 ≤ α < 1
принадлежит L
1
(ku(t)k
1
= 1/(1 − α)), но не L
2
(интеграл от 1/t
2α
расходится в нуле
при α ≥ 1/2) или L
∞
.
&%
'$
L
∞
&%
'$
L
1
L
2
Рис. 1.2: Пространства L
1
, L
2
, L
∞
.
Условно соотношение между рассмотренными пространствами можно изобразить в
виде диаграммы на рис. 1.2. В частности, из ограниченности функции в L
1
-норме и
L
∞
-норме следует ограниченность в L
2
-норме:
kuk
2
2
=
∞
Z
0
|u(t)||u(t)|dt ≤ kuk
∞
∞
Z
0
|u(t)|dt = kuk
∞
kuk
1
.
1.3.2 Нормы операторов
Нормы функций дают возможность определить и нормы линейных операторов.
Если линейный оператор L (1.23) переводит функции из L
p
в функции из L
q
, где p, q =
1, 2 или ∞ (т.е. если Lu ∈ L
q
при u ∈ L
p
), то его (p, q)-индуцированная норма равна
kLk
p,q
.
= sup
kuk
p
6=0
kLuk
q
kuk
p
= sup
kuk
p
≤1
kLuk
q
. (1.26)
Заметим, что аналогичным образом определяются и индуцированные нормы для мат-
риц (см. Приложение, раздел 5).
Некоторые из операторных норм особенно важны; в частности, случаи p = q = 2 и
p = q = ∞. Мы увидим в дальнейшем, как вычисляются эти нормы через передаточные
функции системы. Так, мы покажем, что
kLk
2,2
= kH(s)k
∞
,
30 Глава 1. Описание линейных систем
где kH(s)k
∞
означает H
∞
-норму передаточной функции системы (см. ниже).
Можно вычислять норму оператора и с помощью весовой функции, т.е. представле-
ния (1.24). Несколько забегая вперед, рассмотрим простейший пример. Пусть (1.22) —
устойчивая система (подробнее см. Гл. 3)) с одним входом и одним выходом. Тогда ее
весовая функция
h(t) = Ce
At
B ∈ L
1
,
так как |Ce
At
B| ≤ const ·e
−σt
, σ > 0, и поэтому
Z
∞
0
|Ce
At
B|dt < ∞. Покажем, что имеет
место формула для оператора L, задающего систему (1.24):
kLk
1
.
= kLk
∞,∞
= khk
1
. (1.27)
Действительно, для kuk
∞
≤ 1 имеем
|y(t)| ≤
t
Z
0
|h(t − τ )||u(τ)|dτ ≤
t
Z
0
|h(t − τ )|dτ ≤ khk
1
,
поэтому kyk
∞
≤ khk
1
. С другой стороны, зафиксировав t и взяв u
0
(τ) = sign h(t − τ)
при 0 ≤ τ ≤ t и u
0
(τ) = 0 при τ > t, имеем
y(t) =
t
Z
0
h(t − τ )u
0
(τ)dτ =
t
Z
0
|h(t − τ )|dτ = khk
1
−
∞
Z
t
|h(τ)|dτ.
Отсюда следует, что y(t) сколь угодно близк´о к khk
1
при больших t, т.е. sup
t
|y(t)| = khk
1
.
Норма оператора является мерой того, насколько он “усиливает” входные сигналы,
измеряемые в соответствующей норме. Обычно желательно выбрать управление так,
чтобы эта норма была по возможности мала; это означает, что выход системы будет
мал при любых возмущениях, ограниченных в соответствующей норме.
Аналогичные пространства и нормы вводятся для дискретного случая. Здесь нужно
рассматривать не функции y(t) на [0, ∞), а последовательности y
0
, y
1
, . . . , y
i
, . . ., где
y
i
∈ R
l
. Для них вводятся пространства l
p
и нормы в них определяются следующим
образом:
1) l
2
: kyk
2
=
Ã
∞
X
i=0
|y
i
|
2
2
!
1/2
,
2) l
∞
: kyk
∞
= sup
0≤i<∞
|y
i
|,
3) l
1
: kyk
1
=
∞
X
i=0
|y
i
|.
Например, если y
i
≡ 1 или y
i
= sign(−1)
i
, то y ∈ l
∞
, но y /∈ l
2
, y /∈ l
1
, а для
y
i
= 1/(i + 1)
α
будет y ∈ l
∞
при любом α > 0, y ∈ l
2
при α > 1/2, y ∈ l
1
при α > 1.
