Полоцкий Л.М., Лапшенков Г.И. Автоматизация химических производств
Подождите немного. Документ загружается.

154
Переходную характеристику системы будем находить с использованием
операционного исчисления. Для получения решения преобразуем все слагаемые
уравнения (IV,41) по Лапласу с учетом начальных условий. По определению и в
соответствии с выражениями (5), (6), (16), приведенными в Приложении 1, имеем
(
)
( )
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
( )
(
)
(
)
Учитывая эти соответствия, а также выражение (4), приведенное в Прило-
жении 1, получим
(
)
(
)
(
)
Откуда изображение искомой величины равно
(
)
(IV, 44)
Для нахождения оригинала y(t) по этому изображению из характеристи-
ческого уравнения системы
(IV, 45)
определим его корни. Они равны
(
) √(
)
(
)
(IV, 46)
Если (k
0
k
p
+1)
2
>4k
0
T
0
/T
И
, то оба корня вещественные и разные. В этом слу-
чае выражение (IV,44) приводят к форме
(
)
(
)
(
)
и, учитывая соотношение (28). Приложения 1, получают
(
)
Вычислив разность р
1
—р
2
√
(
)
(
)
окончательно получим
(
)
√
(
)
(
)
(
) (IV, 47)
В данном случае переходный процесс носит апериодический характер.
155
При (k
0
k
p
+1)
2
<4k
0
T
0
/T
И
корни характеристического уравнения (IV,45) ком-
плексные сопряженные
Где
√
(
)
В этом случае выражение (IV,44) представим в виде
(
)
( )
и, принимая во внимание соотношение (31), приведенное в Приложении,
получим
(
)
Или
(
)
√
(
)
√
(
)
(IV, 48)
Уравнение (IV,48) описывает колебательный процесс.
Если (k
0
k
p
+1)
2
=4k
0
T
0
/T
И
, то корни характеристического уравнения веще-
ственные и равные
Тогда, представив выражение (IV.44), в виде
(
)
( )
и учитывая соотношение (29), приведенное в Приложении, получим
(
)
Или
(
)
(IV, 49)
Это граничный апериодический процесс.
Таким образом, при возмущении z=1(t) переходный процесс в исследуемой
системе описывается уравнениями (IV,47) — (IV,49) и может иметь разный харак-
тер (рис. IV-10). Во всех трех случаях статическая ошибка регулирования у
равна
нулю, т. е. введение в систему ПИ-регулятора превращает ее в астатическую.

156
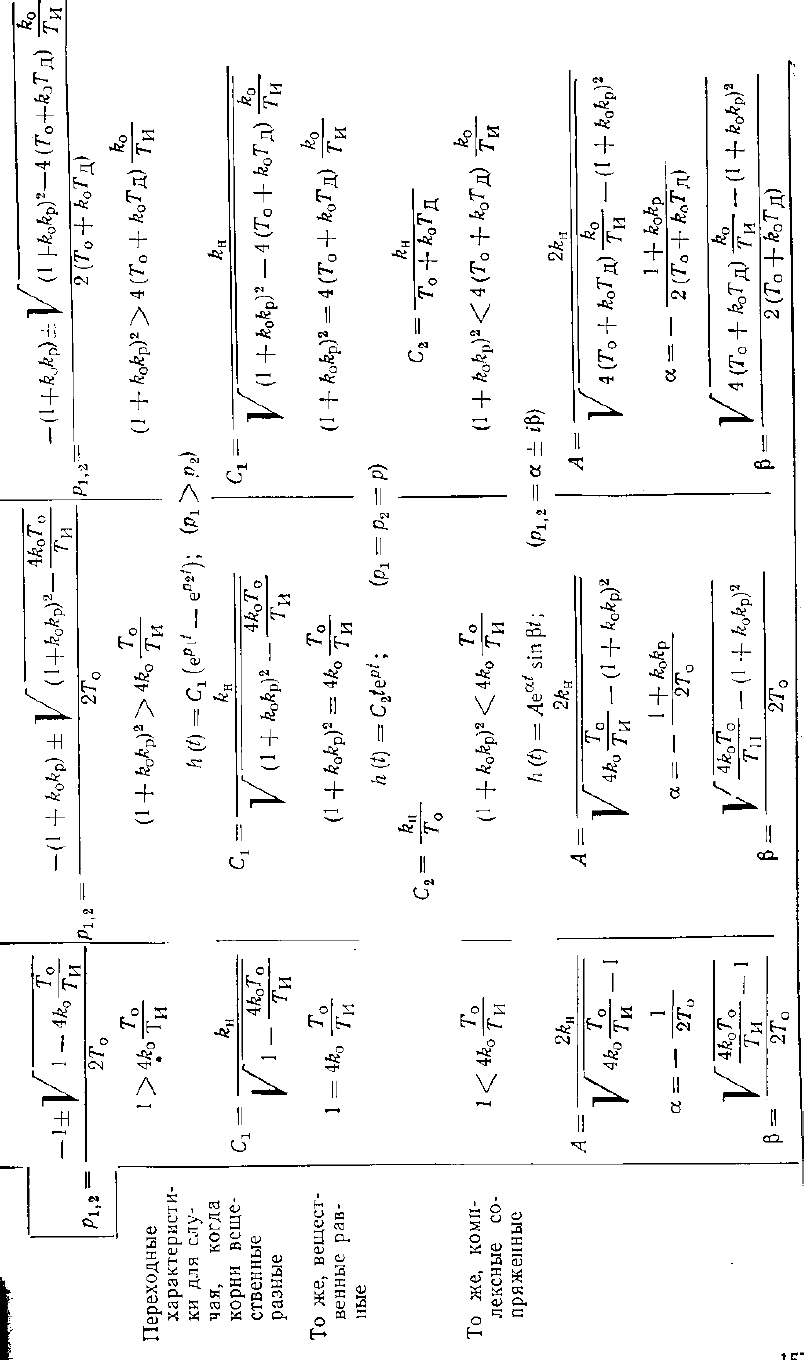
Таблица IV.6. Уравнения динамики и переходные характеристики систем с
устойчивым объектом 1-го порядка
157

158
Рис. IV-10. Переходная характеристика системы 2-го порядка, снабженной
ПИ-регулятором, в случае апериодического (1), граничного апериодического (2) и
колебательного (3) переходных процессов.
Уравнения динамики и переходные характеристики для систем 2-го поряд-
ка, состоящих из устойчивого объекта 1-го порядка, снабженного И-, ПИ- или
ПИД-регулятором, сведены в табл. IV.6.
Из уравнений переходных характеристик следует, что в этих системах воз-
никают переходные процессы таких же форм, что и приведенные на рис. IV-10.
При регулировании устойчивого объекта 1-го порядка И - регулятором ис-
чезает статическая ошибка регулирования и система превращается в астатическую.
При апериодическом переходном процессе его длительность в основном
определяется экспонентой с большей постоянной времени, равной
√
(
)
которая более чем в два раза превышает постоянную времени объекта Т
0
.
Увеличение времени интегрирования Т
И
затягивает продолжительность переходно-
го процесса. Увеличение быстродействия регулятора (уменьшение Т
И
) вплоть до
значения, равного Т
И
=4k
0
Т
0
, приводит к уменьшению длительности переходного
процесса и некоторому снижению динамической ошибки регулирования.
Последующее уменьшение Т
И
и приводит к колебательности переходного
процесса. Причем с уменьшением Т
И
колебательность увеличивается, так как
уменьшается период колебаний
√
(
)
Однако одновременно с этим уменьшается и амплитуда колебаний, что не-
сколько снижает динамическую ошибку регулирования. Длительность переходного
процесса, определяемая интенсивностью затухания колебаний, зависит только от
инерционных

159
свойств объекта; постоянная времени экспоненты равна 2Т
0
. Таким образом, наряду
с улучшением статических свойств в системе с И-регулятором наблюдается ухуд-
шение динамических свойств.
Введение П-составляющей уменьшает длительность переходного процесса,
так как постоянные времени определяющих ее экспонент, во всех случаях имеют
меньшее значение, чем при использовании И-регулятора. Причем это влияние уси-
ливается с увеличением коэффициента усиления регулятора k
p
. При ПИ-
регулировании динамическая ошибка всегда меньше, чем при И-регулировании.
Так при равенстве (1 +k
o
k
p
)
2
= 4k
0
T
0
/T
И
она меньше в (1 + k
0
k
p
) раз. С увеличением k
p
период колебаний повышается, т. е. колебательность переходного процесса умень-
шается. Следовательно, применение ПИ-регулятора наряду с улучшением статиче-
ских свойств системы приводит к улучшению всех показателей качества по срав-
нению с системой, использующей И-регулятор. Причем, это улучшение зависит от
значения коэффициента усиления регулятора k
p
.
Введение Д-составляющей в ПИ-закон регулирования не нарушает астатиз-
ма системы. Влияние Д-составляющей, как и в случае с ПД-регулятором, выража-
ется в том, что в первый момент времени после нанесения возмущения скорость
отклонения выходной величины системы с ПИД-регулятором в (1 + k
0
T
Д
/T
И
) раз
меньше, чем при ПИ-регулировании. А поскольку выходная величина системы по-
сле нанесения возмущения и окончания переходного процесса должна строго вер-
нуться к заданному значению, динамическая ошибка ,и время регулирования будут
иметь значительно меньшие значения, чем при ПИ-регулировании. Колебатель-
ность переходного процесса при этом также уменьшается. Таким образом, введе-
ние Д-составляющей в ПИ-закон регулирования улучшает все показатели качества
переходного процесса.
В табл. IV.7 приведены уравнения динамики и переходные характеристики
систем 2-го порядка, состоящих из устойчивого объекта 2-го порядка с П- или ПД-
регулятором.
В системах 2-го порядка с устойчивыми объектами переходные процессы
обладают более высокими показателями качества, чем с нейтральными объектами.
В системе же, включающей нейтральный объект 1-го порядка и И-регулятор, воз-
никает гармонический, колебательный процесс
(
)
√
√
(IV, 50)
с амплитудой и частотой колебаний соответственно равными
√
√
т.е. такая система находится на границе устойчивости.

160
Таблица IV.7. Уравнения динамики и переходные характеристики систем с
устойчивым объектом 2-го порядка
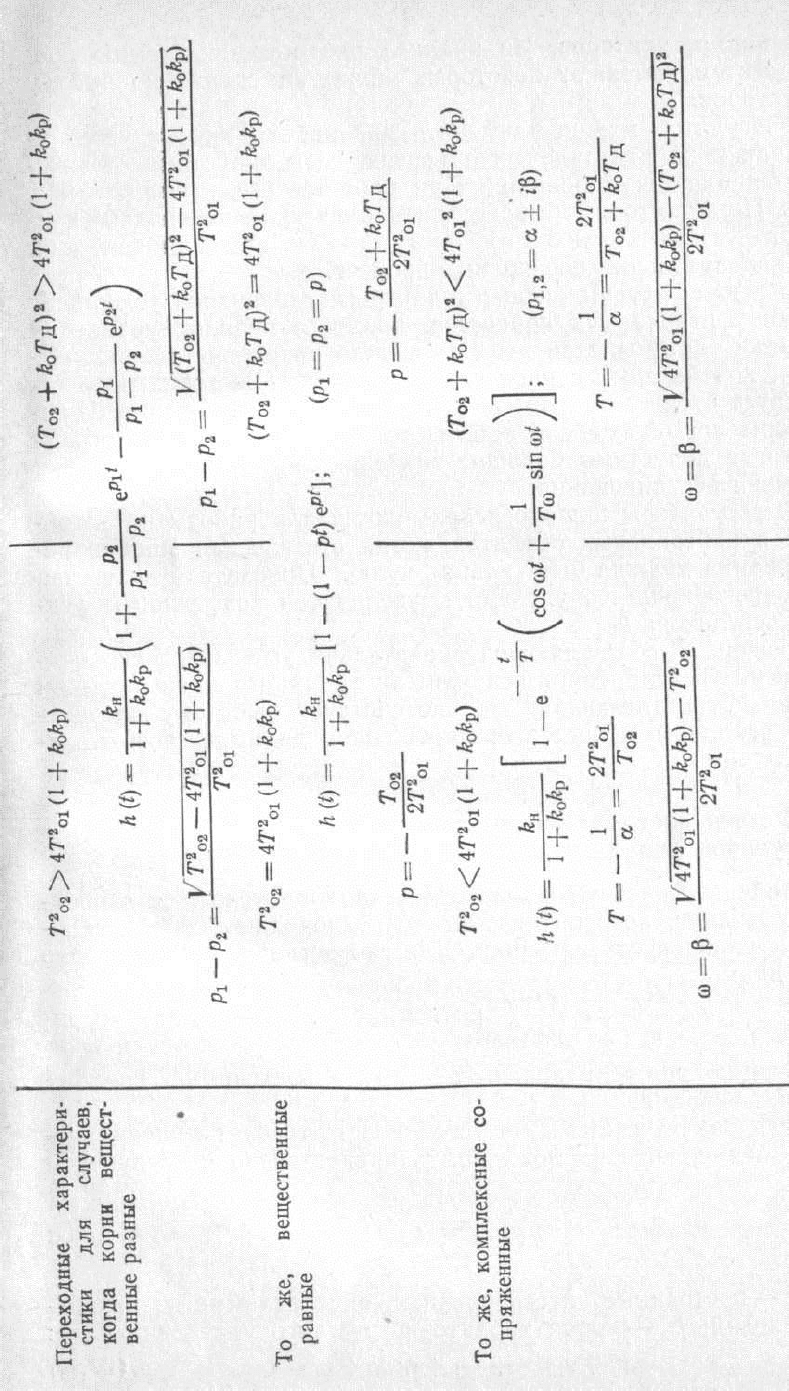
161

162
Выбор регуляторов. Из анализа рассмотренных выше простых систем вы-
текают некоторые общие замечания по выбору регуляторов.
П-регулятор можно применять для работы как на устойчивых, так и на
нейтральных объектах, если допустима статическая ошибка регулирования. При
работе с объектами 1-го порядка П-регулятор формирует апериодический переход-
ный процесс, а — с объектами 2-го порядка — либо апериодический, либо колеба-
тельный переходный процесс.
Введение И-составляющей в закон регулирования усложняет динамику пе-
реходных процессов, повышая порядок уравнения динамики системы. При этом
возможно появление апериодических и колебательных процессов. Наличие И-
составляющей гарантирует отсутствие статической ошибки регулирования. И-ре-
гуляторы применяют для работы только на устойчивых объектах, когда допустимы
большие значения динамической ошибки и времени регулирования.
ПИ-регуляторы широко используются для работы на устойчивых и
нейтральных объектах, когда ститическая ошибка регулирования должна быть
равна нулю. Показатели качества переходного процесса улучшают, увеличивая ко-
эффициент усиления регулятора k
p
.
Введение Д-составляющей значительно уменьшает скорость отклонения ре-
гулируемой величины от заданного значения; если имеется И-составляющая, это
способствует быстрому протеканию переходного процесса при небольшом дина-
мическом отклонении.
4. Устойчивость автоматических систем
регулирования химико-технологических объектов
Устойчивость системы определяется характером ее свободного движения,
которое описывается однородным дифференциальным уравнением динамики. Для
системы n-ого порядка оно имеет вид:
(IV, 51)
где у— выходная величина; а
1
, а
2
,…, а
п
— постоянные коэффициенты; t —
время.
Исследование системы на устойчивость требует решения этого уравнения,
которое может быть представлено в следующем виде:
(
)
∑
(IV, 52)
где А
к
— постоянные интегрирования, определяемые из начальных условий;
р
к
— корни характеристического уравнения вида
(IV, 53)
163
Однако достаточно просто решаются дифференциальные уравнения только 1-го и
2-го порядков. Решение уравнений более высокого порядка требует преодоления
определенных трудностей, возрастающих c повышением порядка уравнения. Зна-
чительно проще можно найти корни характеристических уравнений. Поэтому це-
лесообразно выяснить зависимость между устойчивостью системы и значением
корней ее характеристического уравнения.
Устойчивость системы и корни характеристического уравнения. Распо-
ложение корней характеристического уравнения позволяет судить об устойчивости
системы. Если характеристическое уравнение имеет только вещественные и разные
корни, то характер изменения каждой составляющей
(
)
зависит от знака корня характеристического уравнения р
к
. При рк = 0 со-
ставляющая y
K
(t) принимает постоянное по времени значение, равное А
к
. Если ко-
рень характеристического уравнения р
к
положителен, то с течением времени соот-
ветствующая ему составляющая переходного процесса y
K
(t) увеличивается до
.бесконечности; если же корень р
к
отрицателен, то — стремится к нулю (рис. IV-
11).
В случае, когда характеристическое уравнение кроме вещественных имеет
сопряженные комплексные корни
каждой паре таких корней в решении (IV,52) соответствуют составляющие
вида
(
)
(
)
(
) (IV, 54)
где А и φ — новые постоянные интегрирования.
Напомним, что только при наличии сопряженных комплексных корней все
коэффициенты характеристического уравнения действительны. Составляющая пе-
реходного процесса (IV,54) имеет колебательный характер.
Изменение амплитуды колебательной составляющей во времени зависит от
знака вещественной части α
k
комплексных корней. При α
k
= 0 амплитуда колеба-
тельного процесса не изменяется во времени, т.е. наблюдается гармонический ко-
лебательный процесс. Если вещественная часть пары комплексных корней по-
ложительна, то амплитуда колебательного процесса с течением времени возрастает
до бесконечности, если же вещественная часть отрицательна, то — уменьшается и
стремится к нулю (рис. IV-12).
Система устойчива лишь в случае, когда все слагаемые y
K
(t) в решении
(IV,52) со временем стремятся к нулю. Если все корни характеристического урав-
нения системы вещественные отрицательные или комплексные с отрицательной
вещественной
