Полоцкий Л.М., Лапшенков Г.И. Автоматизация химических производств
Подождите немного. Документ загружается.


144
Регулируемая величина — уровень жидкости — измеряется преобразовате-
лем, сигнал с выхода которого направляется на вход ПИ-регулятора. Выход регуля-
тора— регулирующее воздействие — поступает на исполнительное устройства ти-
па НЗ, изменяющее расход жидкости из аппарата. При увеличении уровня жидко-
сти ее расход из аппарата должен увеличиваться, и наоборот. Структурная схема
этой системы приведена на рис. IV-7,б.
Уравнения динамики отдельных элементов системы приведены в табл. IV.2;
при этом принято, что заданное значение регулируемой величины постоянно и и
равно нулю.
Исключим из системы уравнений табл. IV-2 переменные у
1
, x
1
и х. Для этого
последовательно подставим y
1
из выражения (III,21) в уравнение (III,27)
∫
(IV, 19)
а найденное выражение для x
1
— в I,27; получим
∫
(IV, 20)
Далее выразим х из уравнения (II,21)
и продифференцируем его
Затем подставим полученные значения х и dx/dt в уравнение (IV,20). В ре-
зультате найдем
∫
(IV, 21)
145
Продифференцируем полученное и сгруппируем слагаемые, содержащие y в
левой части, а содержащие z — в правой части уравнения:
(
)
(
)
(IV,
22)
Разделив все слагаемые на коэффициент при у = k
ИП
k
ИУ
/T
И
получим уравне-
ние динамики рассматриваемой системы
(
)
(
)
(IV,
23)
Окончательно представим уравнение (IV,23) в общем виде
(IV, 24)
Где
(
)
(
)
По структурной схеме и передаточным функциям элементов
АСР можно составить уравнение динамики АСР, если известны структурная
схема и уравнения динамики отдельных ее элементов. Для этого сначала находят
передаточные функции элементов системы и по известным правилам преобразова-
ния структурных схем определяют передаточную функцию всей системы. По этой
передаточной функции, найдя предварительно операторное уравнение системы,
определяют ее дифференциальное уравнение динамики.
Для иллюстрации этих сведений составим уравнение динамики АСР тем-
пературы жидкости на выходе из теплообменника, воздействуя на подачу греюще-
го пара (рис. IV-8, а). Температура жидкости на выходе из теплообменника (регу-
лируемая величина) измеряется термоэлектрическим термометром, работающим в
комплекте с преобразователем, на выходе которого формируется стандартный
пневматический сигнал, подаваемый в качестве текущего значения температуры на
ПИД-регулятор. На регулятор подается также постоянный сигнал, пропорциональ-
ный заданному значению температуры. Регулятор вырабатывает регулирующее
воздействие и направляет его на, исполнительное устройство типа НО, установ-
ленное на линии подачи греющего пара в теплообменник.
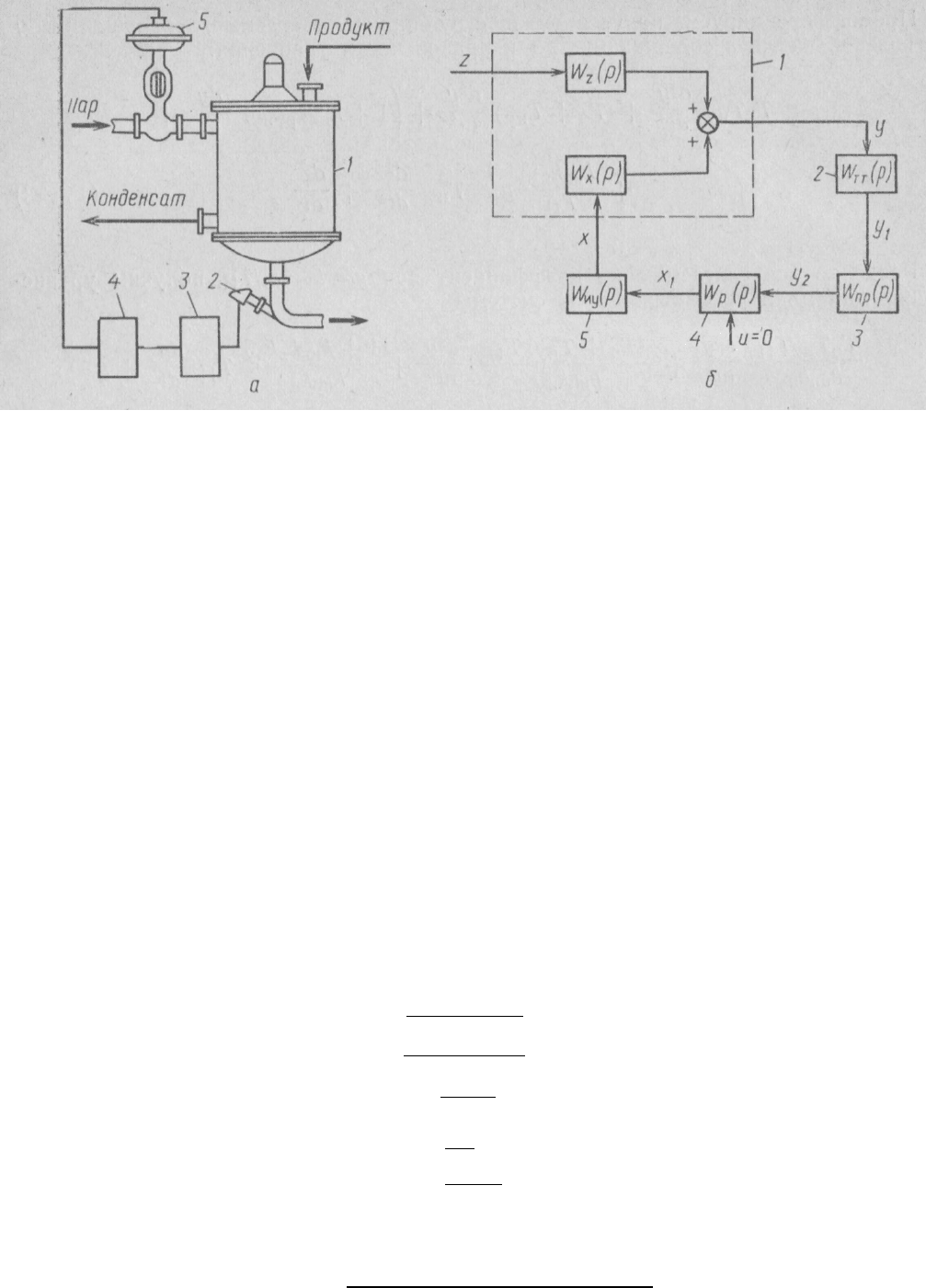
146
Рис. IV-8. Схема АСР температуры жидкости в теплообменнике (а) и струк-
турная схема (б):
1 — теплообменник; 2 — термоэлектрический термометр; 3 — электроп-
невмопреобразователь; 4 — регулятор с вторичным прибором; 5 — исполнитель-
ное устройство.
При наличии возмущения, например, при изменении температуры жидкости
на входе в теплообменник, температура жидкости на выходе из него начнет изме-
няться. В этом случае регулятор должен подать на исполнительное устройство та-
кую команду, чтобы при возрастании температуры жидкости на выходе подача
греющего пара уменьшилась, а при падении — увеличилась. Структурная схема
АСР температуры приведена на рис. IV-8, б.
Уравнения динамики отдельных элементов системы даны в табл. IV.3, при
этом принято, что u = 0.
Согласно табл. IV.3 в замкнутом контуре системы четыре элемента прямого
действия и только один элемент — исполнительное устройство типа НО — об-
ратного действия. Поэтому обратная связь в системе отрицательна.
По уравнениям динамики элементов системы найдем их передаточные
функции:
(
)
(
)
(
)(
)
(
)
(
)
(
)
(
)
}
(IV, 25)
Передаточная функция системы по каналу z→у в соответствии с ее струк-
турной схемой (рис. IV-8, б) определяется равенством
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(IV, 26)

147
Таблица IV.3. Уравнения динамики элементов АСР температуры жидкости на вы-
ходе из теплообменника
Подставляя в это уравнение передаточные функции (IV,25) и перемножая
сомножители в числителе и знаменателе, получим
(
)
(IV, 27)
Где
(
)
(
)
(
)
(
)
(
)
(
)
[
(
)]
[
)]
(
)
(
)
Отсюда при нулевых начальных условиях уравнение динамики в опе-
раторной форме имеет вид
(
)
(
)
(
) ( )
(IV, 28)
а дифференциальное уравнение динамики — соответственно вид
(IV, 29)
По полученным уравнениям динамики АСР могут быть найдены временные
характеристики, передаточные функции, характеристические уравнения и частот-
ные характеристики с помощью тех же приемов, что были изложены в гл. I.
148
3. Исследование простых систем
Исследование работы простой системы сводится к построению се переход-
ной характеристики. По виду последней определяют устойчива ли система и удо-
влетворяет ли она заданному качеству регулирования. Для построения переходной
характеристики решают уравнение динамики системы при единичном ступенчатом
возмущающем воздействии.
Системы 1-го порядка. Исследуем одноконтурную замкнутую систему (см.
рис. IV-6, а), состоящую из устойчивого объекта 1-го порядка и П-регулятора. Для
нахождения уравнения динамики системы составим уравнения динамики объекта и
регулятора со структурной схемой, приведенной на рис. IV-6, в; получим
(IV, 30)
(IV, 31)
где у— регулируемая величина; х— регулирующее воздействие; z— возму-
щающее воздействие; Т
0
— постоянная времени объекта; k
0
и k
н
— коэффициенты
передачи объекта по каналам регулирующего и возмущающего воздействий; k
р
—
коэффициент передачи регулятора; t — время.
Знак минус в правой части уравнения (IV,30) позволяет сформировать кон-
тур с отрицательной обратной связью.
Исключим из уравнений (IV,30) — (IV,31) переменную х
(
)
Разделив слагаемые этого уравнения на коэффициент (k
р
k
о
+1), получим
уравнение динамики системы в общепринятой форме
(IV, 32)
Решим это уравнение при единичном ступенчатом возмущении z=1(t) ,и пу-
левых начальных условиях.
Общее решение у
общ
однородного уравнения, соответствующего уравнению
(IV,32), имеет вид:
(IV, 33)
где С — постоянная интегрирования.
Частное решение y
част
неоднородного уравнения (IV.32) при единичном воз-
мущающем воздействии равно
( ) (IV, 34)
Следовательно, полное решение уравнения (IV,32) при z=1(t) имеет вид
(IV, 35)
Постоянную интегрирования С определим из начальных условий: t=+0; у=0.
Тогда

149
Подставляя значение С в уравнение (IV,35), окончательно получим
(
)
(
) (IV, 36)
Таким образом, переходная характеристика системы, состоящей из устой-
чивого объекта первого- порядка и П-регулятора, имеет экспоненциальный харак-
тер.
Аналогичным образом могут быть найдены уравнения динамики и переход-
ные характеристики и других систем 1-го порядка. Они приведены в табл. IV.4.
Графики переходных характеристик систем 1-го порядка приведены в табл.
IV.5 сплошными линиями, а объектов регулирования— пунктирными линиями.
Сравнение переходных характеристик устойчивого объекта 1-го порядка и
системы, состоящей из того же объекта и П-регулятора, показывает, что скорости
изменения их выходных величин в момент времени t= + 0, т.е. сразу же после нане-
сения возмущения, одинаковы и равны
( )
Со временем скорости изменения у объекта и системы постепенно умень-
шаются до нуля. Это свидетельствует об их устойчивости. Переходный процесс в
системе имеет такой же вид, что и у объекта, но заканчивается значительно быст-
рее и устанавливается на новом значении со статической ошибкой регулирования,
равной
(IV, 37)
Она меньше, чем у объекта в 1/(1+k
0
k
p
) раз. По сравнению с инерционно-
стью объекта инерционность системы также уменьшается, поскольку их постоян-
ные времени связаны соотношением
( )
(IV, 38)
где T
c
— постоянная времени системы.
Время регулирования системы t
рс
, которое для экспоненциальной формы
переходного процесса принимается равным примерно
также будет меньше, чем время регулирования объекта

150
Таблица IV.4. Уравнения динамики и переходные характеристики систем
1-го порядка
151
Таблица IV.5. Графики переходных характеристик объектов (пунктир) и
систем (сплошная линия) 1-го порядка
Следовательно, использование П-регуляторов на устойчивых объектах 1-го
порядка приводит к улучшению качества регулирования. Показатели качества ре-
гулирования (статическая ошибка регулирования и время регулирования) умень-
шаются с увеличением коэффициента усиления регулятора.
Установка П-регулятора на нейтральном объекте 1-го порядка приводит к
устойчивому переходному процессу со статической ошибкой регулирования
(IV, 39)
и постоянной времени
(IV, 40)
Скорости изменения выходных величин объекта и системы в момент време-
ни t=+0 одинаковы и равны k
H
/T
0
.
152
Таким образом, применение П-регуляторов в системах 1-го порядка стаби-
лизирует переходный процесс и улучшает его статические и динамические показа-
тели качества по сравнению с объектом. Статическая ошибка регулирования у
и
время регулирования t
p
зависят от величины коэффициента усиления регулятора k
р
.
Увеличивая k
р
, можно уменьшить у
и t
p
до значений, не превышающих допусти-
мые по технологическим соображениям.
Введение дифференциальной составляющей в пропорциональный закон ре-
гулирования (см. табл. IV.4 и IV.5) приводит к уменьшению скорости изменения
выходной величины системы в начальный момент времени по сравнению со скоро-
стью изменения выходной величины объекта в 1+ (k
0
T
Д
/T
0
) раз. Это в свою очередь
приводит к тому, что инерционность системы становится пропорционально больше
и время регулирования возрастает. На величину статической ошибки регулирова-
ния Д-составляющая не влияет.
Следовательно, применение ПД-регуляторов может быть оправдано в тех
случаях, когда па систему подаются частые и большие по величине возмущающие
воздействия.
Регулирование объектов П- или ПД-регуляторами всегда сопровождается
статической ошибкой регулирования, определяемой по равенствам (IV,37) и
(IV,39). Такие системы называют статическими. Их статические характеристики
приведены на рис. IV-9. Тангенс угла наклона статической характеристики устой-
чивого объекта (k
р
= 0) определяется отношением
а для нейтрального объекта равен
При включении регулятора (k
р
>0) наклон статической характеристики си-
стемы уменьшается. С увеличением
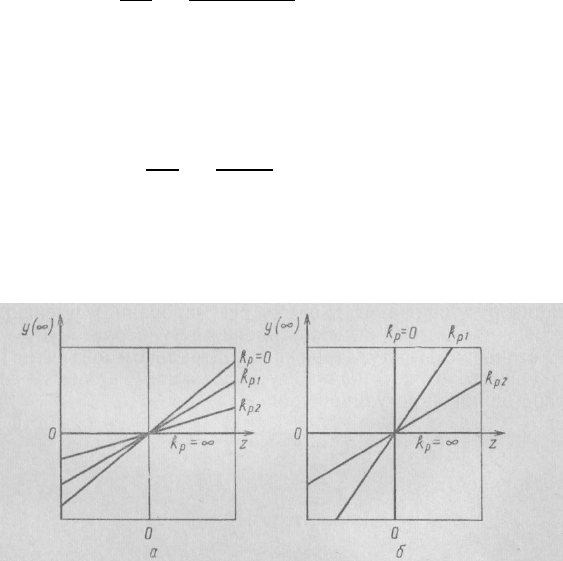
Рис. IV-9. Статические характеристики систем с устойчивым (а) и нейтраль-
ным (б) объектами при различных значениях k
p
.
153
коэффициента усиления регулятора k
р
(на рисунке 0<k
р1
<k
р2
<∞) статическая харак-
теристика системы поворачивается по часовой стрелке, уменьшая статизм системы.
Теоретически при k
р
= ∞ статическая ошибка регулирования становится равной ну-
лю.
В действительности максимальное значение коэффициента усиления регу-
лятора ограничивается реальной конструкцией регулятора; кроме того при боль-
шом значении k
p
начинает сказываться влияние второстепенных факторов, не учи-
тываемых при выводе уравнения динамики (запаздывание при передаче сигналов,
наличие люфтов и зазоров в кинематических парах и др.). Влияние этих факторов
приводит к колебательному процессу и увеличению времени регулирования.
Системы, у которых при изменении возмущающего воздействия z статиче-
ская ошибка регулирования равна нулю, называются астатическими. В координа-
тах y
∞
, z их статическая характеристика представляет собой горизонтальную пря-
мую.
Астатическая система должна содержать в своей структуре астатические
(интегрирующие) звенья, причем, если они находятся в прямой цепи передачи воз-
действия или в цепи обратной связи, то система обладает астатизмом, а если они
находятся в цепи, охваченной обратной связью, то система будет статической.
Системы 2-го порядка. К ним относятся, например, системы с устойчивым
объектом первого порядка и И-, ПИ- или ПИД-регуляторами. Аналитический ана-
лиз таких систем сложнее.
В качестве примера разберем случай, когда система состоит из устойчивого
объекта 1-го порядка и ПИ-регулятора, уравнения динамики которых имеют вид:
∫
где T
и
— время интегрирования регулятора.
Исключая из уравнений динамики объекта и регулятора переменную х, по-
лучим уравнение динамики системы
(IV, 41)
Найдем переходную характеристику системы, т. е. ее реакцию на единичное
возмущение z=l(t), при условии, что до нанесения возмущения система имела ну-
левые начальные условия у(—0)=0 и dy(—0)/dt=0. Так как правая часть уравнения
(IV,41) содержит производную, начальные условия системы необходимо привести
к моменту t = +0. Учитывая порядок левой (п = 2) и правой (m = 1) частей уравне-
ния (IV,41), согласно табл. 1.2 имеем
(
)
(
)
(IV, 42)
( )
( )
( )
(
)
(IV, 43)
