Петров Ю.П. Очерки истории теории управления

Подождите немного. Документ загружается.

§ 5. Встреча с проблемой сохранения устойчивости...

коителей качки судна "Академик Курчатов" оптимальное управ-

ление имеет вид:

,.„ >ил]

—

ц.

^л-)

—

^.^^л^

И =•

90л:,-6.15л;,-3.35л;,

118л, -

0.035О + 0.85

где Л|,л-

,Лз — соответственно, сигналы от гироакселерометра,

гиротахометра и кренометра. Оптимальное управление легко реа-

лизуется и обеспечивает дисперсию остаточной качки в 2,7 раза

меньшую, чем ранее используемые законы управления ([1],

стр.

227—232).

Для синхронного генератора, подающего питание на Азербайд-

жанский трубопрокатный завод, оптимальный регулятор, реали-

зованный Н. Д. Абдуллаевым в 1983—-84 годах, имел вид

'„

0.274

19.3О + 10.3

11.8 +

2.780 +

8.82Г>

+3.970 + 1;

х,

где х — отклонение напряжения от номинального, легко реали-

зовывался на основе простого усилительного, апериодического

и колебательного звеньев и обеспечивал существенное увеличе-

ние качества напряжения в заводской сети ([1], стр. 209—215).

Самое важное свойство оптимальных регуляторов, синтезированных

по методике, предложенной в [187, 195], заключается в том, что

замкнутые ими системы не меняют существенно своих свойств

(устойчивости, величины критерия качества и т. п.) при отклоне-

ниях параметров объекта управления, регулятора или возму-

щающих воздействий от значений, принятых при расчете.

§ 6. Развитие методов

расчета нелинейных

систем управления

В истории развития нелинейных систем, автоматического управ-

ления и методов их расчета трудно выделить какую-либо перио-

дичность. Методы расчета нелинейных систем предлагались еще

в XIX веке и продолжают развиваться до самых последних лет.

Однако наиболее важный вклад в теорию нелинейных систем

внесли исследования академика Александра Александровича

Андронова (1901—1952) и созданной им в г. Горьком научной

школы.

Для теории и практики автоматического управления и регулиро-

вания наибольшую роль играет не численное решение нелиней-

ных дифференциальных уравнений, описывающих нелинейные

системы управления, а проблема общих характеристик их пове-

дения. А. А. Андронов сумел найти подходящий для решения

этой проблемы математический аппарат — качественную теорию

дифференциальных уравнений, в которой установившиеся режимы

нелинейных систем управления отображались в виде предельных

циклов на фазовой плоскости или в фазовом пространстве. Этот

аппарат дал А. А. Андронову и его сотрудникам необходимое

"идейное вооружение" (любимое выражение Андронова), позво-

лившее решить обширный крут практических задач. По образно-

му выражению Г. С. Горелика, Андронов стал "охотником за

предельными циклами", а его ученики шутили: "Александр Алек-

сандрович живет не в обычном, а в фазовом пространстве" ([255],

том

1,стр.

53—54).

58 § 6.

Развитие методов расчета нелинейных систем управления

Важным этапом в исследовании нелинейных систем стал в 1937 г.

выход в свет монографии "Теория колебаний", написанной

А. А. Андроновым в соавторстве с А. А. Виттом и С. Э. Хай-

киным [10]. Помимо многочисленных примеров исследования

предельных циклов конкретных нелинейных систем в моногра-

фии [10], а также в статье [11], был впервые рассмотрен важней-

ший вопрос о "грубости" линейных и нелинейных систем и их

математических моделей: поскольку "мы никогда не можем с аб-

солютной точностью описать реальную систему при помощи

математического аппарата" (см. [10], стр. 33), а кроме того, "ни

одна реальная система не остается неизменной во время проис-

ходящих в ней процессов, то мы всегда должны допускать воз-

можность малых изменений вида дифференциальных уравнений.

И если мы приписываем параметрам модели вполне определен-

ные фиксированные значения, то это имеет смысл лишь при ус-

ловии, что малые изменения параметров не изменяют существен-

но характера движений, и в поведении идеальной модели

сохраняются те черты, которые нас интересуют". Далее в [10] на

той же стр. 33 делается главный вывод: теоретическими моделя-

ми реальных физических и технических систем могут быть лишь

те,

которые не меняют существенно своего поведения при малых

изменениях параметров или вида дифференциальных уравнений

(с оговоркой — эти изменения не должны изменять порядка сис-

темы).

Подобные системы в монографии [10] было предложено

называть "грубыми", и именно "грубые" системы стали после

1937 г. предметом изучения всех последующих исследователей,

"негрубые" системы почти всегда физического смысла не имеют.

Мы убеждаемся, что монография [10] действительно оказала ре-

шающее влияние на выбор направления всех дальнейших науч-

ных исследований, хотя это было признано далеко не сразу.

Только постепенно, через много лет (да и то не окончательно),

было все же признано, что перед тем, как начать исследовать,

или рекомендовать к практическому применению любую систе-

му, нужно проверить, является ли она "грубой" или нет, потому

что "негрубые" системы практического смысла почти никогда

не имеют.

$ 6. Развитие методов расчета нелинейных систем управления 59

Отметим, что в последние десятилетия термин "грубые системы"

стали часто заменять на заимствованный из английских и амери-

канских публикаций термин "робастные системы".. В такой заме-

не нет никакой необходимости, поскольку английский термин

имеет тот же смысл, что и русский, и мы лишь напрасно прини-

жаем приоритет наших великих соотечественников, которые еще

г; 1937 г. поняли смысл и значение разделения систем на "гру-

бые"

и "не грубые". А за рубежом это было понято лишь много

позже.

Заметим еще, что оговорка, сделанная в [10] на стр. 33—34 (ого-

ворка о том, что "грубые" системы не меняют существенно своих

свойств при вариациях параметров, но при условии, что эти ва-

риации не изменяют порядка системы), является существенной и

выводит из рассмотрения особые системы, открытые лишь в 1991 г.

Особые системы не менее опасны, чем "не грубые", и мы расска-

жем о них в § 13.

Жизнь и деятельность А. А. Андронова подробно описаны в кни-

ге Е. С. Бойко [28]. Там же приведены и яркие выдержки из не-

опубликованных записей лекций Андронова по истории автома-

тического управления и регулирования: "Уаттовские регуляторы,

честно работавшие во времена Уатта, с увеличением мощности

машин уже к середине XIX века перестали надежно работать.

Инженеры заподозрили самый принцип регулятора Уатта. Каза-

лось,

что сам принцип порочен. Думали, что чем меньше нерав-

номерность (статизм), тем лучше регулятор. Стали искать способы

уменьшения неравномерности, предлагали новые конструкции,

новые механизмы. Но знаменитый Чебышев показал, что и не

меняя конструкции Уатта, можно сделать регулятор с любой, са-

мой малой неравномерностью. Но Чебышев своей замечательной

работой толкал людей в совершенно неправильном направлении,

наводя на ложный путь уменьшения неравномерности. В статике

малая неравномерность хороша, но вот в динамике... Ди-

намическое мышление нам трудно дается, у нас статическая пси-

хология. Трудности, связанные с игрой сил инерции, гироскопи-

ческие эффекты, нами прямо не учитываются. Мы должны

воспитывать наше мышление, наши наглядные представления,

опираясь на формулы; это очень важно".

3 'Зак 3820

60 § 6.

Развитие методов расчета нелинейных систем управления

"Динамическую картину регулирования — продолжал А. А. Ан- I

дронов — динамику взаимодействия машины и регулятора уста- {

новил И. А. Вышнеградский, и он показал, что в ряде вопросов ;

дело обстоит обратно тому, что думали. Думали — надо умень- ]

шать неравномерность, а он показал: "без неравномерности нет

регулятора" (знаменитый "второй тезис"). Ведь гениальный Че-

бышев этого не понимал, а Вышнеградский понял. Гениальный

Чебышев, в сущности, наводил регуляторщиков на ложный

путь..."

(цитирую по книге

[28],

стр. 157—158).

После безвременной кончины А. А. Андронова в 1952 г. исследо-

вания продолжали его сотрудники и ученики (горьковская школа

Андронова). Подробнее о ней рассказано в уже упоминавшейся

книге [28].

Не останавливаясь подробно на различных методах расчета про-

цессов, протекающих в нелинейных системах управления (методы

гармонического баланса, статистической линеаризации, гармо-

нической линеаризации, метод сечений в пространстве парамет-

ров,

предложенный Р. А. Нелепиным [164, 165] и др.), рассмот-

рим историю поисков критерия устойчивости для системы,

состоящей из линейного объекта управления и регулятора,

в котором зависимость управляющего воздействия и от сигнала

рассогласования а в цепи обратной связи является нелинейной,

т.е.

/(о), причем

(54)

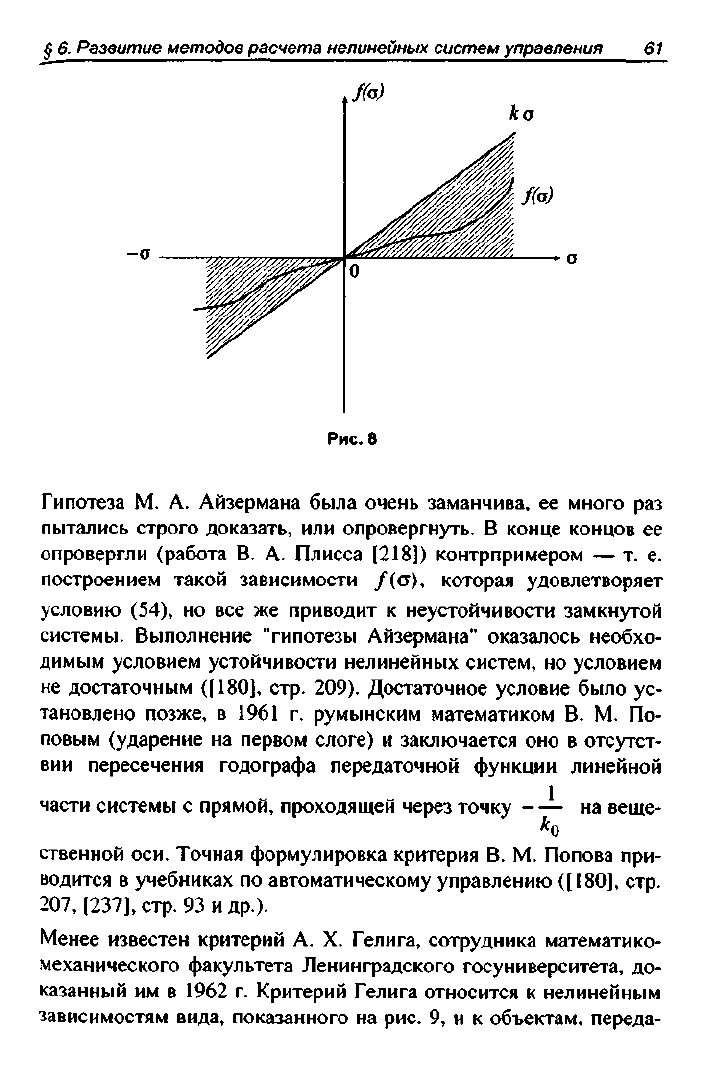
т. е., как показано на

рис.

8, функция /(а) лежит внутри сектора,

ограниченного прямыми и

0 и и

с.

История поисков критерия устойчивости интересна тем, что

в начале ее лежала правдоподобная гипотеза, высказанная

М. А. Айзерманом (1913—1992) в работе [3]: необходимым и

достаточным критерием устойчивости нелинейной системы с за-

висимостью и от а, соответствующей формуле (54), является

устойчивость всех линейных систем, в которых и

ко,

для всех

0<*<*

$ 6. Развитие методов расчета нелинейных систем управления 61

Рис.8

Гипотеза М. А. Айзермана была очень заманчива, ее много раз

пытались строго доказать, или опровергнуть. В конце концов ее

опровергли (работа В. А. Плисса [218]) контрпримером — т. е.

построением такой зависимости /(с), которая удовлетворяет

условию (54), но все же приводит к неустойчивости замкнутой

системы. Выполнение "гипотезы Айзермана" оказалось необхо-

димым условием устойчивости нелинейных систем, но условием

не достаточным ([180], стр. 209). Достаточное условие было ус-

тановлено позже, в 1961 г. румынским математиком В. М. По-

повым (ударение на первом слоге) и заключается оно в отсутст-

вии пересечения годографа передаточной функции линейной

части системы с прямой, проходящей через точку на веще-

го

ственной оси. Точная формулировка критерия В. М. Попова при-

водится в учебниках по автоматическому управлению ([180], стр.

207,

[237],

стр. 93 и др.).

Менее известен критерий А. X. Гелига, сотрудника математико-

механического факультета Ленинградского госуниверситета, до-

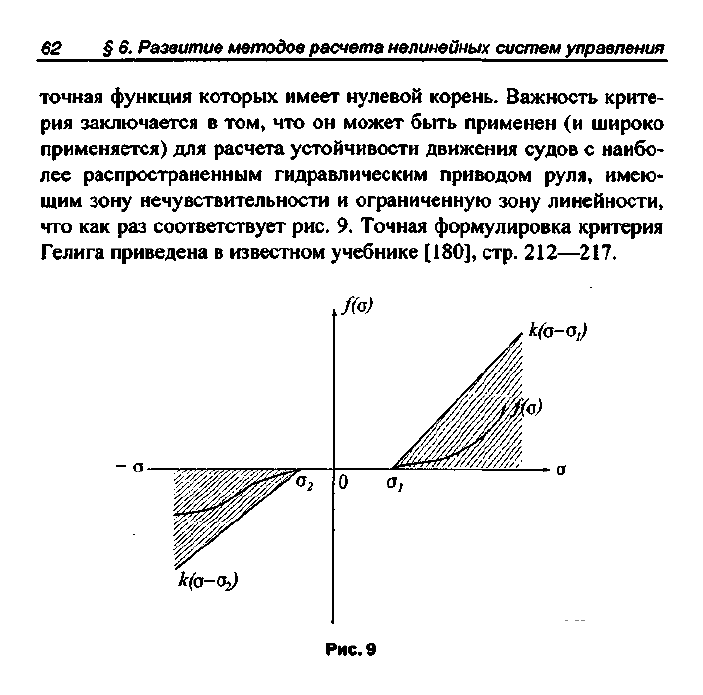
казанный им в 1962 г. Критерий Гелига относится к нелинейным

зависимостям вида, показанного на рис. 9, и к объектам, переда-

62 §

Развитие методов расчета нелинейных систем управления

точная функция которых имеет нулевой корень. Важность крите-

рия заключается в том, что он может быть применен (и широко

применяется) для расчета устойчивости движения судов с наибо-

лее распространенным гидравлическим приводом руля, имею-

щим зону нечувствительности и ограниченную зону линейности,

что как раз соответствует рис. 9. Точная формулировка критерия

Гелига приведена в известном учебнике

[180],

стр. 212—217.

Рис.9

§ 7. Переход к поискам

оптимальных программ

управления

Следующим этапом в истории развития автоматического управ-

ления и регулирования стал постепенный переход ко все более

и более широкому поиску и применению оптимальных программ

управления.

До поры до времени программы движения, которые затем отсле-

живались с помощью средств управления, выбирались на основе

эмпирических соображений, но потом стали все чаще вспоми-

нать,

что в математике существует аппарат (вариационное исчис-

ление), позволяющий выбирать наилучшие, оптимальные про-

граммы. Переход к использованию оптимальных программ стал

новым важным этапом как в истории прикладной математики,

так и в истории автоматического управления.

Начало этого этапа можно отнести к 50-м гг. XX века, хотя пер-

вые оптимальные программы управления тягой ракет были рас-

считаны Гамелем (О. Нате1) еще в 1927 г.

[105].

Затем были ра-

боты Тзяна и Эванса

[105],

Охоцимского и Энеева [175] и много

других работ. В области ракетной техники все шло гладко, по-

скольку программы изменения тяги ракет с самого начала рас-

считывались методами вариационного исчисления как програм-

мы оптимальные. Других программ управления, не оптимальных,

но ставших привычными, здесь не было, конкурировать было не

с кем, и построение оптимальных программ для самых различ-

ных вариантов полета ракет шло беспрепятственно и бескон-

фликтно.

64 § 7.

Переход

поискам оптимальных программ управления

Совсем по-другому обстояло дело в тех областях техники, где до

1950 г. программы движения объектов управления выбирались из

эмпирических соображений. Программы эти с годами сделались

привычными, и отказ от них, переход на более совершенные про-

граммы, найденные с использованием вариационного исчисле-

ния, далеко не всегда проходил гладко и часто сопровождался

ожесточенными (и даже злобными) нападками на новые методы.

Так, в 1950 г. профессор Борис Львович Давыдов из Харькова

рассчитал наивыгоднейшую программу подъема грузов из руд-

ников, обеспечивавшую существенное повышение производи-

тельности рудничного оборудования. Б. Л. Давыдов использовал

для расчета методы вариационного исчисления, причем он уди-

вительно изобретательно преодолел трудности, связанные с не-

достаточной тогда разработанностью этих методов для техниче-

ских задач. Решение Б. Л. Давыдова было опубликовано в № 11

журнала "Уголь" за 1950 г. [76], а уже в № 7 следующего года

в том же журнале были помещены резко критические отклики на

его статью сразу пяти авторов во главе с академиком АН УССР

В.

С. Паком [77], самым непримиримым образом отвергавших

все рекомендации Б. Л. Давыдова. Исчерпав технические аргу-

менты, его оппоненты перешли к доводам политическим: "мета-

физическое отношение проф. Давыдова привело его к надуман-

ной, абстрактной теории, которая применима как будто везде, а в

действительности — нигде. Марксизм учит, что абстрактной ис-

тины нет, истина всегда конкретна" [77]. После этих резких от-

зывов Б. Л. Давыдов прекратил свою работу в области поиска

оптимальных программ. Через

лет, в 1963 г., когда вариацион-

ное исчисление уже очень широко применялось в теории автома-

тического управления, я написал Б. Л. Давыдову в Харьков,

спрашивая, не собирается ли он в новых условиях продолжить

свои исследования, столь блистательно начатые им в 1950 г. Он

ответил: "Мне уже поздно. Силы ушли. Да и слишком тяжелые

воспоминания связаны у меня с той давней моей статьей".

Не меньшие препоны и трудности пришлось преодолеть и в об-

ласти оптимизации электрических приводов, несмотря на то, что

для приводов постоянного тока вариационная задача не была