Петров Ю.П. Очерки истории теории управления

Подождите немного. Документ загружается.

§ 3. Расчеты систем управления...

Книга Н. Винера "Кибернетика" известна и популярна из-за своей

первой части (страницы

5—80

русского перевода), где очень ярко

обрисована роль обратной связи, роль информации не только

в технических системах, но и в природе, и человеческом общест-

ве;

материал, изложенный на страницах 81—ПО, был доступен

для понимания очень малому кругу лиц.

Только несколько позже уже другие ученые коренным образом

улучшили изложение результатов теории случайных процессов.

В ее основе лежит понятие корреляционной функции Л

(т) ста-

ционарного случайного процесса

ц>(г),

определяемой равенством

(т)= Нт— Гф(ОФ(г + т)А. (18)

т—>°°

27 _

Корреляционная функция отражает тесноту связи между зна-

чениями (р(г), разделенными временем т. При т = 0 получаем

средний квадрат ф(0> обозначаемый обычно угловыми скобками:

/ \ 1 '

(ф

)= Нт— |ф

(/)Л =

(0).

(19)

В приложениях очень часто встречаются корреляционные функ-

ции, близкие к экспоненте:

(т) = (ф

)^'

. (20)

Заметим, что хотя в формулу (18) входит интегрирование по бес-

конечному промежутку, в действительности хорошее приближе-

ние к корреляционной функции можно получить, интегрируя из-

меренные значения ф(?) и ф(г + т) на совсем умеренном

интервале [-Г;+Г]. Корреляционная функция, таким образом,

вычисляется несложно, а затем к ней применяют косинус-

преобразование Фурье— т.е. А-

(т) умножают на созшт. интег-

рируют по т и получают функцию 5

((о), которую называют

§ 3.

Расчеты систем

управления...

спектром (или спектральной плотностью мощности) процесса

(р(0:

(со) = —

|А:

(т) сое тек. (21)

Если, например,

(т) =

е~

ат

, то, вычисляя интеграл (21), по-

лучаем:

(со)=- ° (22)

я а

-2

со

Наиболее важным свойством спектральных плотностей мощно-

сти является то, что для них операция дифференцирования пере-

ходит в гораздо более простую операцию умножения на квадрат

модуля комплексного числа /со. Действительно, если у

их, то

спектры функций у(() и х{1) связаны простым равенством

5/со)

|усо|

5,(со).

Из этого равенства следует, что для вычисления среднего квадра-

та <х > решения х(() линейных дифференциальных уравнений

вида (16), где А(й) — гурвицев полином, имеет место простая

формула:

(х

) = ]5

(со)

й(й

(23)

Таким образом, если ф(0 — случайный процесс, то вычислить

само решение х(1) уравнения (16) невозможно, но зато средний

квадрат решения вычисляется по формуле (23) очень просто.

то

же время знание среднего квадрата говорит весьма много о ре-

шении х(1). Значения случайного процесса чаще всего распреде-

лены по нормальному закону, и тогда имеет место простое соот-

ношение: вероятность Р того, что значение х(1) не превысит

§ 3. Расчеты систем управления...

величины кс

(где а

=Мх )) , зависит только от к и выра-

жается формулой:

Р(\х\<ко

)

Ф(к), (24)

где Р — вероятность, а Ф(к) — известный "интеграл веро-

ятностей" (называемый еще интегралом Лапласа)

к У

Ф{к)

^=\е~

с1у, (25)

л/2Яо

для которого были давно составлены подробные таблицы.

В частности, если к

то Ф(А') =

0,9973.

Это означает, что

с вероятностью 0,9973 — т. е. с практической достоверностью —

модуль функции х(1) не превысит трех среднеквадратичных от-

клонений.

Данное соотношение позволяет легко производить практические

расчеты.

Пример: пусть мы для конкретного судна вычислили, пользуясь

формулами (18), (21) и (23), что среднеквадратичный угол крена

5°,

а опасность опрокидывания для данного судна начинает-

ся с крена 0 =

20°.

Тогда на основе формулы (25) мы делаем дос-

товерное заключение: максимальное значение угла крена не пре-

вышает 3-5° =

15,

и поэтому данная качка не опасна, к опроки-

дыванию судна она не приведет.

Начиная с 50-х годов XX века, простая формула (23) лежит в ос-

нове расчета качки судов на реальном, нерегулярном волнении,

расчета следящих систем, систем управления [83, 169, 194, 247,

248] и многих других расчетов.

Что касается расчета оптимального регулятора, обеспечиваю-

щего наилучшее качество управления, то здесь все сложнее. Дело

в том, что поиск оптимального регулятора — это, фактиче-

ски,

поиск оптимального оператора, наилучшим образом преоб-

разующего функцию х(1) на входе регулятора в функцию н(г),

§ 3.

Расчеты систем

управления...

где и — управляющее воздействие на его выходе. В свое время

Н. Винер предложил следующую классификацию математиче-

ских объектов в порядке их возрастающей сложности:

Функция — она ставит в соответствие числу (аргументу функ-

ции) другое число — значение функции. Дифференциальное

исчисление позволяет найти аргумент, доставляющий макси-

мум (или минимум) функции.

Функционал (пример — определенный интеграл) — он ставит

в соответствие функции число — значение функционала. Ва-

риационное исчисление позволяет найти функции, достав-

ляющие максимум (или минимум) функционалам.

Оператор (пример — оператор дифференцирования) — он

функции ставит в соответствие другую функцию. Пока не су-

ществует математического аппарата, позволяющего система-

тически находить операторы, оптимальные в том или другом

смысле.

В последнее время термин "оператор" получил другие опреде-

ления; однако классификация Н. Винера наиболее наглядна и

подчеркивает трудность задачи поиска оптимального оператора.

§ 4. Синтез регуляторов,

доставляющих минимум

среднеквадратичному

критерию качества

Трудная задача синтеза регулятора, доставляющего минимум

среднеквадратичному критерию качества при наличии не пол-

ностью известных возмущающих воздействий случайного харак-

тера, постепенно решалась разными путями в начале второй по-

ловины XX века (работы [26, 31, 156. 159, 169, 247, 248, 268]).

В основе всех путей к решению лежат переход в частотную об-

ласть, использование спектров возмущающих воздействий и со-

отношений (23), позволивших свести задачу поиска наилучшего

оператора к задаче поиска функции, доставляющей экстремум

среднеквадратичному функционалу.

Для пояснения возникавших у исследователей трудностей изло-

жим один из путей решения проблемы синтеза регулятора для

простейшего объекта управления вида

Д(О)л- = н+ф(0, (26)

где х — регулируемая переменная (точнее, ее отклонение от же-

лаемого для нас значения, соответствующего х

0), Л(О) — по-

лином от оператора дифференцирования вида (12), и — управ-

ляющее воздействие, (р(0 — возмущающее воздействие,

стационарная случайная функция времени со средним значением,

равным нулю, для которой предполагается известной корреляци-

§ 4.

Синтез

регуляторов...

онная функция

К^{х),

или, что то же самое, с учетом равенства

(21) — ее спектр 5

(о)).

Для объекта управления (26) ставится задача о поиске линейного

регулятора с обратной связью вида

№(0)х

_ ЩР)

Щ(О)

(27)

где Щ{й) и Щ(й) — полиномы от оператора дифференци-

рования. Этот регулятор должен обеспечить минимум функ-

ционалу

{х

)

\\т^\х

<И

(Т.

е. среднему квадрату регулируемой переменной) при учете

ограничения на средний квадрат управляющего воздействия:

(и

)

Ит^и

а(

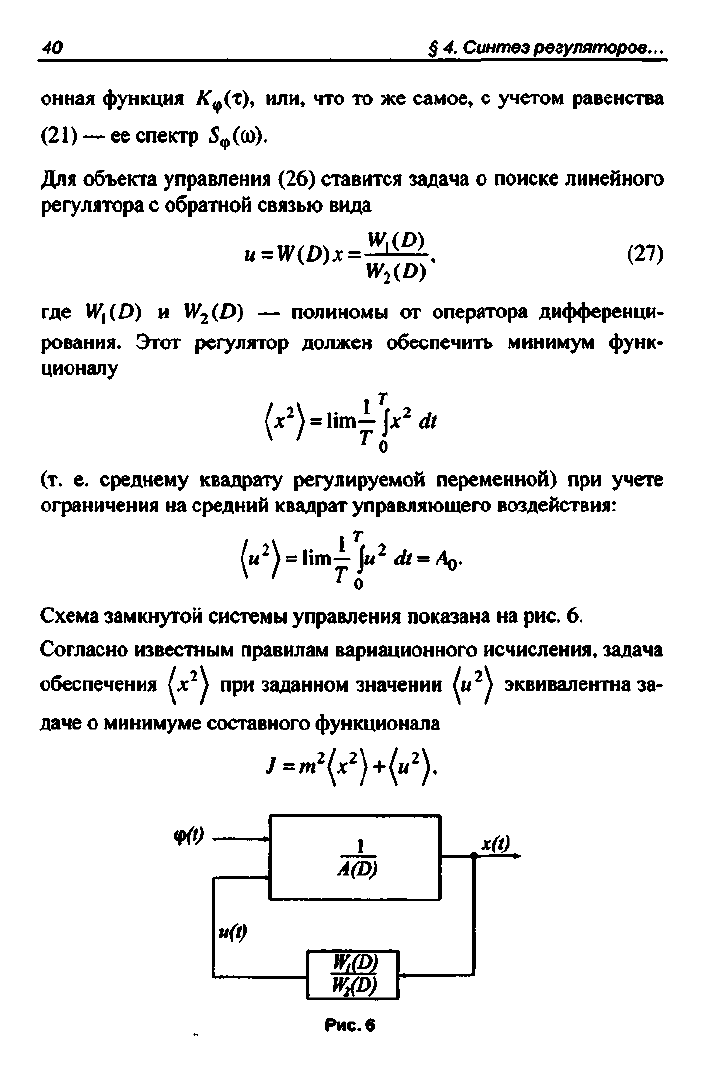
Схема замкнутой системы управления показана на

рис.

Согласно известным правилам вариационного исчисления, задача

обеспечения (х

) при заданном значении (и

) эквивалентна за-

даче о минимуме составного функционала

)

(и

Рис.6

Синтез

регуляторов...

где т — множитель Лагранжа, постоянное (неотрицательное)

число, подлежащее в дальнейшем определению.

Сформулированная задача не очень хорошо отражает реальные

требования к системам управления, поскольку в реальных систе-

мах почти всегда ограничен не средний квадрат, а предельное

значение управляющего воздействия:

" тт

—

" тах

•

Однако точное решение задачи синтеза оптимального регулятора

при реальных ограничениях на управление до настоящего време-

ни не получено, и поэтому с давних пор довольствуются ограни-

чением на средний квадрат. Учет этого ограничения даст лишь

приближенное решение задачи о минимуме (х ), однако именно

поиску этого приближенного решения было посвящено большое

количество различных исследований [26, 31, 140, 141, 156, 169,

172,

192, 247, 248, 266, 268].

Из формул (26) и (27) следует, что

[А(0)-\Уф)]х

= <р(1)

и, значит, с учетом формулы (23) имеем:

<1ы

(л

)=|5

(со)

о |ЛОш)-1УОсо)|'

Аналогично вычисляется значение среднего квадрата управления

(и

)=/5

(ш) '

' о |Д(;со)-^(;ш)|

и составного критерия

)

(и

)= 8^(0)- ' ' , Лео. (28)

I о |Л(;ш)-\У(;(0)|

Для вычисления минимума составного критерия достаточно по

обычным правилам вариационного исчисления найти функцию

§4.

Синтез

регуляторов...

И^О'Сй), оставляющую минимум функционалу (28). После неслож-

ных вычислений была получена функция

А(-;СО)

откуда, казалось бы, следует, что оптимальный оператор в цепи

обратной связи имеет вид

__гг

'опт

то)оп

А(-Р)

а оптимальным регулятором является регулятор

•х.

"'"" А(-О)

Однако этот регулятор (как будет далее показано) не обеспечива-

ет устойчивости замкнутой системы, и поэтому при минимизации

критерия (28) допустимы не любые вариации функции И^(у(0),

а лишь те, которые совместимы с устойчивостью. Это обстоя-

тельство потребовало значительно более сложных выкладок при

минимизации функционала (28) (полностью эти выкладки

приведены, например, в

[195],

стр. 59—62), и они приводят,

в конечном счете, к следующему алгоритму синтеза регулятора,

обеспечивающего минимум критерия (28) при дополнительном

условии устойчивости замкнутой системы.

В основу расчета берется аналитическая аппроксимация экспе-

риментальных данных о спектре возмущающего воздействия

ф(г),

спектр аппроксимируется дробно-рациональной функцией:

(29)

"9"

' "<{-

а„$

+а„_1« ^ +... +

ЙЛ

(предварительно в спектре 5

(со) переменная со заменяется

для удобства на переменную

_/(>)).

Далее спектральная

плотность мощности (29) факторизуется

(*) =

(*)$,(-*), (30)

§ 4. Синтез регуляторов...

т. е. представляется, как произведение двух симметричных

множителей 5,0) и 5

(

(—5),

один из которых зависит от 5,

другой — от -\. Поскольку числитель и знаменатель дроби

(29) — функции четные, то они имеют соответственно 1р и 2ц

симметричных корней: Х

]

и -Л,; к

и -к

и т. д. В множи-

тель 5|(я) войдут все корни с отрицательными веществен-

ными частями, в множитель

5,(-л)

войдут все корни с по-

ложительными вещественными частями. Таким образом,

(31)

и числитель, и знаменатель функции 5,(5) являются гурвице-

выми полиномами.

Заметим еще, что величину среднего квадрата возмущающего

воздействия удобно нормировать, т. е. принять раз и навсегда,

что (ф ) =

Поскольку оптимальный регулятор линеен, то

на его расчет нормировка не повлияет.

На втором шаге алгоритма точно так же факторизует-

ся полином

А(х)А(-.ч)

=0(Л')С(-.У) (32)

с целью вычисления полиномов С(х) и С7(-я). При этом

С (а) — гурвицев полином (т. е. у всех его корней веществен-

ные части отрицательны), а С(-х) — не гурвицев.

Выполняется разложение на дроби (сепарация):

(33)

где М

— целый полином, Л/

— правильная дробь с полю-

сами в левой полуплоскости комплексного переменного

х,М

_ — правильная дробь с полюсами в правой полуплоско-

сти А.

§ 4.

Синтез

регуляторов...

Строится функция

(8) ОДЗД'

с помощью которой уже непосредственно находятся поли-

номы

У/

{0)

и Щ(й) в оптимальном регуляторе (27):

Ш1

шМ1

»-*№.

(

35)

Щф) Ф,ф)

Подставив (35) в (26), получим уравнение замкнутой системы:

(д)х

= Ф,(*)ф. (36)

Поскольку, как это следует из формулы (34), полином Ф

($) бу-

дет иметь все корни в левой полуплоскости, то замкнутая система

будет устойчивой.

Мы убеждаемся, что параметры оптимального регулятора вычис-

ляются по довольно сложному алгоритму. Для объектов управле-

ния вида А(0)д: = В(0)м + ф (где В(0)*1), при учете погреш-

ностей измерения и для многомерных систем алгоритм синтеза

оптимальных регуляторов еще намного сложнее. Заметим, что

если не учитывать требования устойчивости, а непосредственно,

методами вариационного исчисления искать регулятор, достав-

ляющий абсолютный минимум функционалу, то мы придем

к уже упоминавшемуся регулятору

и = х. (37)

Подставив (37) в (28), получим уравнение замкнутой системы:

[д(0)Д(-0) + т

]д: = Д(-0)ф(Г). (38)

Характеристический полином уравнения (38) при любом А(О)

будет иметь корни с положительными вещественными частями,

и поэтому замкнутая система будет неустойчива.

Отметим, что это не является непреодолимым препятствием

к реализации оптимального движения объекта управления, опи-