Пеньковский Г.Ф. Основы информационных технологий и автоматизированного проектирования в строительстве
Подождите немного. Документ загружается.


120 121
Для обеспечения необходимой точности и устойчивости счета при-
меняют следующие приемы [17]:
1. Путем итераций подбирают такие значения шага сетки (размер
элемента), при которых точность счета достаточна и устойчивость обес-
печена. По Рунге – Кутту, точность считается достаточной, если при за-
мене шага
X на X/2 результаты счета для основных параметров отли-
чаются не более чем на 5 %.
2. Применяют разные шаги сетки на разных участках объекта или
во времени в МКР, аналогично в МКЭ – разные по размерам элементы,
уменьшенные в области отверстий и сопряжений, и укрупненные супер-
элементы на различных участках расчетной схемы.
3. Вводят искусственную вязкость
в описание математической мо-
дели, применяют итерации с вязкостью.
4. Используют способ обратной связи шагов счета в ДШМ, обеспе-
чивающий сглаживание скачков меняющихся параметров в шагах вы-
числений.
После определения усилий и деформаций в конструкциях произво-
дится расчет прочности сечений.
Нагрузки и прочность материалов обладают природной изменчи-
востью и носят вероятностный
характер. В методе предельных состоя-
ний это обстоятельство учитывается методологией назначения расчет-
ных и нормативных характеристик материалов и нагрузок с помощью
математического аппарата теории вероятностей и математической ста-
тистики.
Изменчивость свойств строительных материалов описывается нор-
мальным законом распределения Гаусса
)
2
)(
(exp
2
1
)(
2
2
G
SG
MR
RP
, (14)
где P(R) – вероятность реализации прочности материала R как случайной
величины (рис. 25, а); М – математическое ожидание прочности материала
при испытании n образцов
¦
n
i
i
R
n
M
1
1
;
G
– среднеквадратическоеое
отклонение,
D G ; D – дисперсия,
¦
n
i
i
MR
n
D
1
2
)(
1
.
ществляется в два этапа. Вначале определяются усилия в элементах кон-
струкций, затем делается расчет по прочности и по деформациям с уточ-
нением размеров поперечных сечений элементов.
Для определения усилий в программных средствах САПР получи-
ли развитие численные методы на основе дискретных в пространстве
и во времени расчетных схем – метод конечных разностей
(МКР), метод
конечных элементов (МКЭ), дискретно-шаговые методы (ДШМ), метод
граничных элементов (МГЭ).
Основная идея МКР состоит в замене точных значений производ-
ных их приближенными значениями через конечные разности функций.
Расчетная схема сооружений представляет собой сетку с заданным ша-
гом по осям координат. Этот метод иногда называют методом сеток.
В МКЭ
конструкция разбивается на систему плоских или простран-
ственных элементов, состояние которых описывается рекуррентными
уравнениями равновесия, совместности деформаций и закона деформи-
рования материала в элементах. Совместное решение уравнений с уче-
том граничных условий раскрывает напряженно-деформированное со-
стояние конструкции.
ДШМ описывают состояние объекта в последовательных дискрет-
ных шагах расчета от начала загружения
с учетом изменения нагрузки
и состояния конструкции в каждом шаге. Это дает возможность доста-
точно просто учитывать нелинейные свойства деформации материалов
и внешних воздействий путем аппроксимации нелинейных функций ку-
сочно-линейными с любой заданной точностью приближения. ДШМ
удобно применять в задачах динамики. Решение на ЭВМ получается до-
статочно просто даже в тех
случаях, когда невозможно получить анали-
тическое замкнутое решение дифференциальных уравнений движения.
Метод граничных элементов состоит в комбинации аналитических
решений теории упругости и пластичности для некоторой центральной
области сечений в конструкциях и приближенных численных способов
решения для краевых участков сечений.
Все численные методы расчета являются приближенными, поэто-
му центральным вопросом их применения для
расчета конструкций на
ЭBМ является обеспечение необходимой точности и устойчивости сче-
та. С уменьшением шагов сетки в МКР или шагов вычислений в ДШМ
точность расчета повышается, но увеличивается при этом трудоемкость
и продолжительность счета. При увеличении шагов может происходить
накопление ошибок, счет оказывается неустойчивым, появляются сбои.
122 123
Для нормативной нагрузки
³
f
t
н
95,0)()(
н
N
dNNPNNP
. (18)
Ус л о ви е прочности конструкций для первой группы предельных
состояний записывается в форме вероятностей математической модели
),,(Ф
pp
J
d RSN
, (19)
где Ф – несущая способность конструкции в функции от ее геометричес-
ких размеров S, расчетной прочности материала
p
R
и условий работы
J
.
Физический смысл условия прочности (19) состоит в том, что мак-
симально возможное значение нагрузки при эксплуатации сооружения
не должно превышать минимальную несущую способность конструк-
ции с доверительной вероятностью не ниже 0,999.
Вероятностные характеристики материалов и нагрузок представ-
лены в нормах [21] их детерминированными значениями. В таблицах
приводятся нормативные и расчетные значения прочности материалов, в
их
связь имеет вид
м
н
p
J
R
R
. (20)
Здесь расчетное сопротивление
p
R
имеет доверительную вероят-
ность не ниже 0,999 за счет деления нормативного сопротивления R
н
(бра-
ковочного минимума, гарантируемого изготовителем с вероятностью 0,95)
на коэффициент надежности по материалу
1
м
!J
.
Расчетная нагрузка в детерминированном виде определяется по
формуле
ннp
NN
J
, (21)
где
н
J
– коэффициент надежности по нагрузке (
1
н
!J
).
Расчетное условие для второй группы предельных состояний имеет
вид
][ ff d
, (22)
где
f
– деформация (или ширина раскрытия трещин в железобетонных
конструкциях), определяемая при нормативных нагрузках и норматив-
ных характеристиках материалов; [
f
] – допускаемое значение деформа-
ции в нормальных условиях эксплуатации.
Отметим, что расчеты по первой группе предельных состояний (по
прочности) как более ответственные, выполняются по расчетным харак-
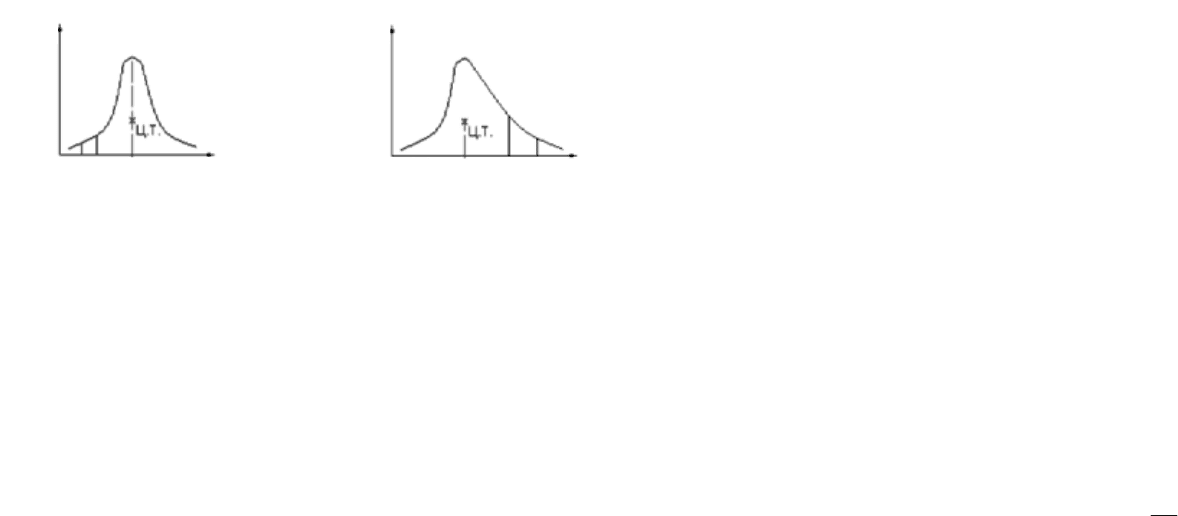
а
б
P(R) P(N)
R
p
R
н
M R
M
N
н
N
p
N
Рис. 25. Законы распределения характеристик для материалов (а)
и для нагрузок (
б) (Ц. Т. – центр тяжестей)
Расчетные и нормативные значения прочности материала (
p
R
и
н
R
)
назначаются так, чтобы доверительная вероятность (обеспеченность)
была для расчетной прочности
³
f
t t
р
999,0)()(
p
R
dRRPRRP
; (15)
для нормативной прочности
³
f
t t
н
95,0)()(
н
R
dRRPRRP
. (16)
Изменчивость нагрузок описывается различным образом. Для на-
грузок от собственного веса конструкций используется нормальный за-
кон Гаусса. В общем случае закон распределения для нагрузок имеет не-
симметричный вид (рис. 25, б). Нагрузки малой величины (от снега, вет-
ра) имеют более высокую вероятность проявления, чем большие нагруз-
ки. Но подход к назначению
и использованию расчетных и нормативных
нагрузок (
p
N
и
)
н
N
по доверительной вероятности реализации такой же,е,
как в оценке прочности материалов. Разница только в том, что если для
материалов представляет интерес область значений прочности
p
RR !
и
н
RR !
, то для нагрузок важны такие их значения, которые при эксплу-
атации сооружения не превышают расчетных и нормативных.
Для расчетной нагрузки
³
f
t
p
999,0)()(
p
N
dNNPNNP
. (17)

124 125
При малых напряжениях в конструкциях, далеких от появления
пластических деформаций, при расчете конструкций в машиностроении,
работающих в упругой стадии, вполне правомерно применять расчет по
допускаемым напряжениям, как более простой и понятный.
2. Оптимизация сечений сжатых и изгибаемых
железобетонных элементов
В сжатых железобетонных элементах усилие сжатия воспринима-
ется бетоном и арматурой пропорционально модулю упругости.
Обычно
напряжения в арматуре на порядок больше напряжений в бетоне, а об-
щее усилие, воспринимаемое арматурой, зависит от содержания армату-
ры в сечении и коэффициента армирования. Если учесть, что единица
прочности 1 МПа для металла на порядок дороже, чем для бетона, то в
сжатом железобетонном элементе целесообразно максимально сжимаю-
щие усилия передать на
бетон. Арматуру же ставить конструктивно с
минимальным коэффициентом армирования.
Для сжато-изогнутых и изгибаемых железобетонных элементов
оптимальное по стоимости проектное решение можно найти с помощью
альтернативного ДЦ (рис. 26).
Уровни ДЦ
Класс бетона
Класс арматуры
Ширина сечения b, мм
Высота сечения h, мм
Рис. 26. Дерево целей
Варьируя все параметры на всех уровнях дерева целей и используя
программу расчета железобетонного сечения (например SCAD), можем
найти потребное количество арматуры в сечении и определить стоимость
1 пог. м элемента
теристикам материалов и нагрузок с обеспеченностью не ниже 0,999.
Расчеты по второй группе предельных состояний (по деформациям) осу-
ществляются при соблюдении условий первой группы. Они
являются про-
верочными и имеют обеспеченность несколько меньше, но не менее 0,95.
Как видим, в основе метода предельных состояний лежит вероят-
ностная математическая модель работы конструкции под нагрузкой, но
для удобства расчетов она приведена к детерминированному виду.
В некоторых странах расчет строительных конструкций осуществ-
ляют по допускаемым напряжениям. Этим методом пользовались и
в
нашей стране до введения метода предельных состояний. Ус л о в ие проч-
ности при этом имеет вид
][VdV
, (23)
где
V
– напряжения в наиболее нагруженной части сечения элемента;
[
V
] – допускаемое напряжение для материала конструкции, определяе-
мое по формуле
k
т
][
V
V
. (24)
Здесь
т
V
– напряжение, при котором начинается разрушение мате-
риала конструкции или появляются пластические деформации текучес-
ти в металлических конструкциях; k – коэффициент запаса, которым учи-
тывается изменчивость свойств материала конструкции и нагрузок.
В методе предельных состояний вместо одного коэффициента за-
паса в расчете присутствуют три коэффициента надежности: по матери-
алу, по нагрузке и
условиям работы. При этом коэффициенты надежнос-
ти по материалу и по нагрузке состоят из двух частей. Первая часть учи-
тывает собственную изменчивость свойств материалов и нагрузок на-
значением нормативных значений с доверительной вероятностью 0,95.
Вторая часть учитывает важность расчетного аппарата назначением до-
полнительного запаса надежности с повышением доверительной веро-
ятности расчетных значений
прочности материала и нагрузок до вели-
чины 0,999.
Такой дифференцированный подход к оценке изменчивости различ-
ных факторов в расчете конструкций дает возможность получать более
экономичные и достаточно надежные проектные решения, чем в методе
расчета по допускаемым напряжениям.
126 127
.
2 b
A
R
R
RA
M
h
s
b
s
ss
(27)
Тогда формула для стоимости одного погонного метра балки (25)
получит вид
11
CC)
2
(C
ssb
s
b
S
ss
A
b
A
R
R
RA
M
b
. (28)
Обозначим
s
b
R
Mb
k
1
1
C
;
1
1
2
C
2
C
s
b
bs
R
R
k
,
получим
s
s
Ak
A
k
2
1
С
. (29)
Взяв производную
s
dA
dС
и приравнивая ее к нулю, получаем выра-
жение для оптимальной площади арматуры в сечении с минимальной
стоимостью
2
2
1
С
kAk
dA
d
s
s
;
0
2
2
1
kAk
s
;
)C2(
2
;
2
1
RR
bM
A
k
k
A
s
ss
, (30)
где
1
1
C
C
C;
s
b
b
s
R
R
R
.
Зная площадь арматуры из уравнениq (26) и (27), находим высоту
сжатой зоны и высоту h для сечения с оптимальными параметрами. За-
метим здесь, что прямоугольное поперечное сечение элемента можно
трансформировать в тавровое (рис. 28) без изменения расчетных формул (30).
При этом достигается дополнительная экономия бетона за счет умень-
шения ширины сечения от b
до
1
b
на высоте h–x. Ширина ребра
1
b
11
CCC
ssbb
AA
, (25)
где
sb
AA ,
– площадь бетона и площадь арматуры в сечении, м
2
;
11
C,C
sb
–
стоимость единицы объема бетона и арматуры.
При конструктивном армировании и малых нагрузках для изготов-
ления элементов целесообразно использовать более дешевые низкопроч-
ные бетоны и стали. При больших нагрузках, когда сечение бетона и ар-
матуры определяется расчетом, выгоднее применять высокопрочные
материалы. Это обстоятельство выявляется направленным перебором
вариантов на уровнях ДЦ при синтезе
проектного решения для сечения
элемента.
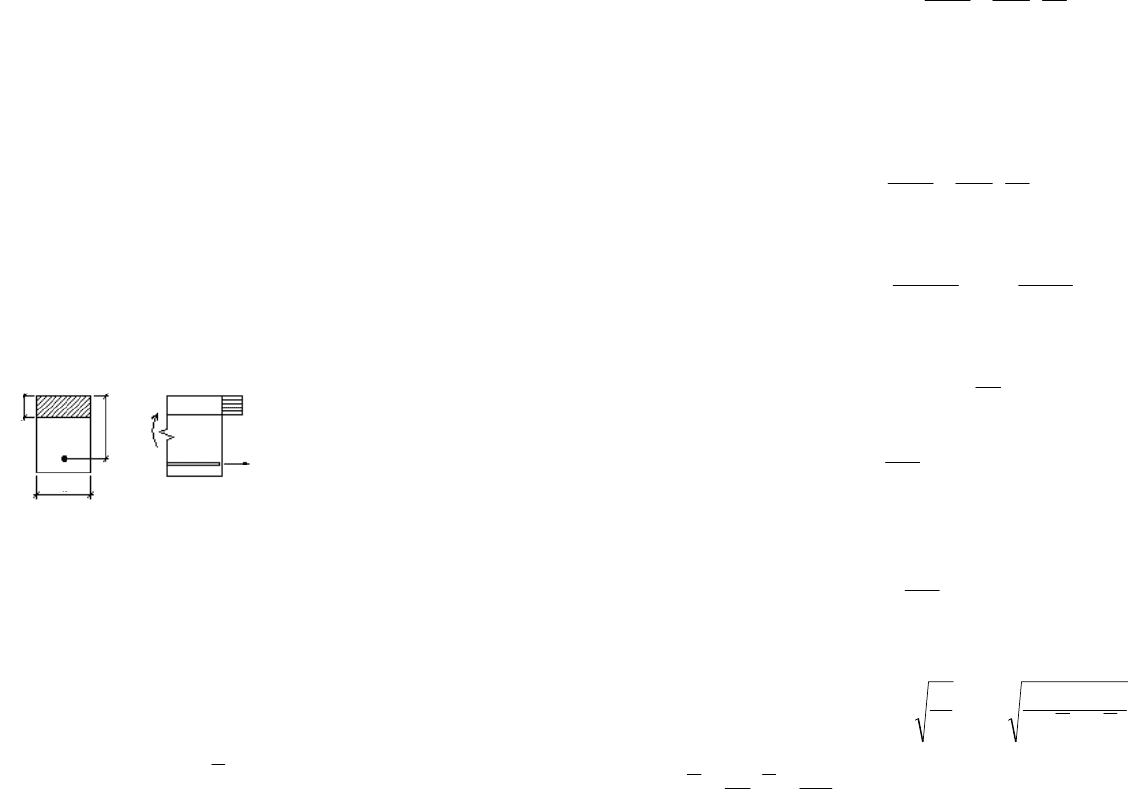
Для изгибаемого элемента с одиночным армированием (рис. 27)
аналитическое решение с получением оптимальных по стоимости пара-
метров сечения можно получить следующим образом:
x
h
b
M
R
b
A
s
R
s
Рис. 27. Сечение элемента
с одиночным армированием
В соответствии с требованиями норм [21] запишем уравнение рав-
новесия для сечения элемента:
°
¿
°
¾
½
).
2
(
;
x
hRAM
ARbxR
SS
SSb
(26)
Здесь
b
R
– расчетное сопротивление бетона; b, h – ширина и высотаа
прямоугольного сечения;
x
– высота сжатой зоны бетона;
ss
AR ,
– рас-
четное сопротивление и площадь арматуры; M – расчетное значение из-
гибающего момента.
Выражая из первого уравнения x и подставляя его во второе, полу-
чим значение высоты сечения
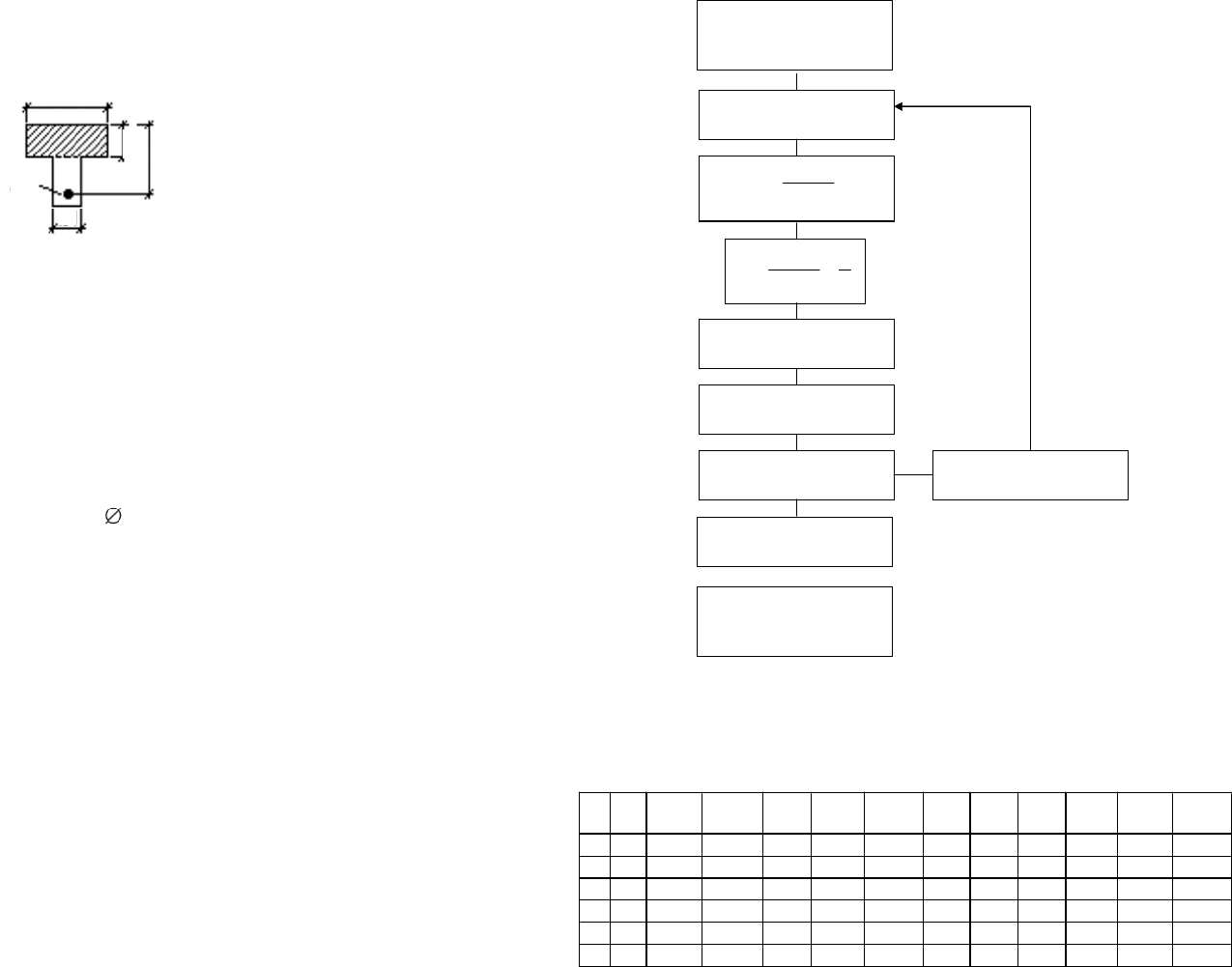
128 129
определяется условиями размещения арматуры
s
A
и необходимостью
восприятия поперечной силы.
b
A
s
x
h
b
1
Рис. 28. Тавровое сечение элемента
Если в сжатой зоне стоит конструктивная арматура
s
A
c
, то формула
(30) дает общую площадь арматуры в сжатой и растянутой зоне сечения.
Представляет интерес получить оптимальные параметры прямоу-
гольного сечения дискретно-шаговым методом с помощью электронных
таблиц Excel с расчетом по алгоритму (рис. 29).
Алгоритм расчета построен с использованием ранее приведенных
формул (26) и (28). Минимальное значение площади арматуры
mins
A
на-
значается конструктивно (например 2
12 мм,
s
A
= 2,26 см
2
). Затем в пер-
вой строке электронной таблицы Exсel записываются все формулы алго-
ритма в адресах ячеек и расчет выполняется автоматически для всех зна-
чений
s
A
, которые назначаем так, чтобы величина стоимости балки С
перешла через экстремум. По данным расчета строятся графики
C,C,C
sb
(рис. 30), при этом относительная высота сжатой зоны не должна превы-
шать граничное значение
).4,0(|[
R
Пример расчета приведен в табл. 6.
Из таблицы и графиков на рис. 29 видно, что оптимальной является
балка с высотой сечения 0,62 м и арматурой
s
A
= 13 см
2
. Аналитическоее
значение этой площади по формуле (30)
s
A
= 13,1 см
2
. На рис. 31 показа-
но армирование балки с такими параметрами.
Аналитический и дискретно-шаговый методы дают возможность
снизить трудоемкость расчета, получить параметры оптимального сече-
ния элемента для последующего окончательного расчета с применением
более сложных программных комплексов.
bR
AR
X
b
ss
2
x
AR
M
h
ss
c
A
s
= A
s
+1C=C
b
+C
s
C
s
= A
s
C
s
1
A
s
= A
s min
C
b
= b h C
b
1
Исходные данные:
M, b, R
b
, R
s
, C
b
1, C
s
1
A
s
= A
s min
Выво
д
:
A
s
, x, h, C
b
, C
s
, C
Рис. 29. Алгоритм расчета параметров сечения
Таблица 6
Расчет параметров сечения
А
s
,
см
2
b, м
R
b
,
кПа
R
s
, кПа
М,
кНм
С
b
,
р./м
3
С
s
,
р./м
3
х, м h, м х/h C
s
, р. С
b
, р. С, р.
1 0,3 13 000 290 000 216 800 94 200 0,01 7,45 0,001 9,4 1788,5 1797,9
2 0,3 13 000 290 000 216 800 94 200 0,01 3,73 0,004 18,8 895,6 914,4
3 0,3 13 000 290 000 216 800 94 200 0,02 2,49 0,009 28,3 598,5 626,8
4 0,3 13 000 290 000 216 800 94 200 0,03 1,88 0,016 37,7 450,5 488,1
5 0,3 13 000 290 000 216 800 94 200 0,04 1,51 0,025 47,1 362 409,1
6 0,3 13 000 290 000 216 800 94 200 0,04 1,26 0,035 56,5 303,3 359,8
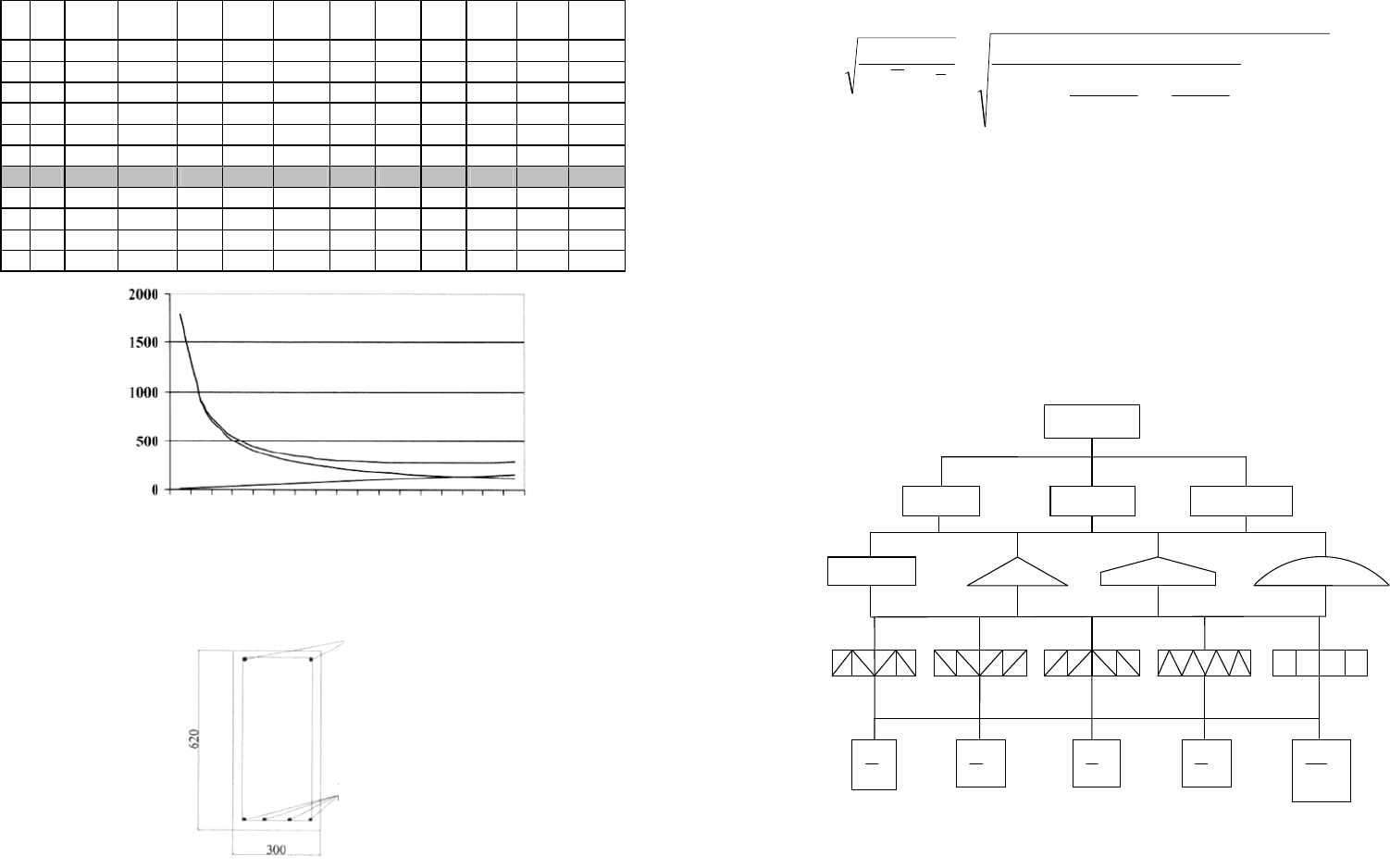
130 131
Окончание табл.6
А
s
,
см
2
b, м
R
b
,
кПа
R
s
, кПа
М,
кНм
С
b
,
р./м
3
С
s
,
р./м
3
х, м h, м х/h C
s
, р. С
b
, р. С, р.
7 0,3 13 000 290 000 216 800 94 200 0,05 1,09 0,048 65,9 261,6 327,6
8 0,3 13 000 290 000 216 800 94 200 0,06 0,96 0,062 75,4 230,6 305,9
9 0,3 13 000 290 000 216 800 94 200 0,07 0,86 0,078 84,8 206,7 291,4
10 0,3 13 000 290 000 216 800 94 200 0,07 0,78 0,095 94,2 187,7 281,9
11 0 ,3 13 000 290 000 216 800 94 200 0,08 0,72 0,114 103,6 172,3 275,9
12 0,3 13 000 290 000 216 800 94 200 0,09 0,67 0,134 113 159,7 272,7
13 0,3 13 000 290 000 216 800 94 200 0,1 0,62 0,156 122,5 149,1 271,6
14 0,3 13 000 290 000 216 800 94 200 0,1 0,58 0,178 131,9 140,2 272,1
15 0 ,3 13 000 290 000 216 800 94 200 0,11 0,55 0,202 141,3 132,6 273,9
16 0 ,3 13 000 290 000 216 800 94 200 0,12 0,53 0,227 150,7 126 276,7
17 0 ,3 13 000 290 000 216 800 94 200 0,13 0,5 0,252 160,1 120,3 280,5
C
s
, C
b
, C, р.
A
s
, см
2
Рис. 30. Графики стоимости бетона
C
b
, арматуры C
s
и балки C = C
b
+ C
s
212 А III
(конструктивно)
412 А III
(А
s
= 12,56 см
2
)
Рис. 31. Армирование балки
Площадь арматуры определяется по формуле (30):
.см1,13
800
20094
2
00013
000290
000290
102163,02
)2(
2
2
8
¸
¸
¹
·
¨
¨
©
§
cRR
bM
A
s
s
3. Оптимизация железобетонных и металлических фермм
Поиск лучших проектных решений для ферм включает в себя по-
строение альтернативного ДЦ с варьированием параметрами, которые
проектировщик может назначать в довольно широких пределах, не на-
рушая требований строительных норм. На рис. 32 приведен пример
такого дерева.
Ферма
Ж/бетон Металл Трубобетон
Варианты
l
6
1
l
7
1
l
9
1
l
8
1
l
10
1
Материал
Очертание
Вид решетки
Средняя высота
Уровни ДЦ
Рис. 32. ДЦ для проектирования ферм

132 133
Критериями для определения лучшего сочетания вариантов на всех
уровнях ДЦ могут быть:
расход бетона или стали;
стоимость материалов;
трудоемкость изготовления фермы;
общая стоимость фермы;
вес фермы;
коэффициент использования материала.
Расчет фермы выполняется с применением программных комплек-
сов (Лира, SCAD или др.), определяется усилие в элементах фермы и
подбирается (или уточняется) сечение элементов фермы.
Ус л о в и е м прочности i-го элемента является коэффициент исполь-
зования прочности материала:
,1
м
d
i
i
i
N
N
K
(31)
где N
i
– усилие в i-м элементе; N
мi
– предельное усилие в i-м элементе,
воспринимаемое материалом.
Для центрально-сжатого железобетонного i-го элемента
,
м ssbbi
RARAN
где А
s
, A
b
– площади арматуры и бетона; R
s
, R
b
– расчетное сопротивление
арматуры и бетона.
Для сжатых элементов железобетонных ферм необходимо прове-
рить условия устойчивости:
N
i i
N
мi
,
где
i
– коэффициент продольного изгиба.
Коэффициент продольного изгиба зависит от отношения расчетной
длины элемента к его меньшему размеру поперечного сечения b (табл. 7).
Таблица 7
Коэффициент продольного изгиба
l/b 10 20 30 40
M
10,80,60,4
Для приближенного определения коэффициента вместо табл. 7
можно воспользоваться формулой
2
40
6,01
¸
¹
·
¨
©
§
M
b
l
.
В металлических фермах коэффициент ц определяется в зависимо-
сти от гибкости сжатых стержней
,
p
i
i
i
r
l
O
где
i
l
p
расчетная длина стержня;
i
r
радиус инерции сечения.
В растянутых элементах железобетонных ферм усилие растяжения
воспринимается арматурой. Но если учесть, что эти элементы обычно
выполняются с преднапряжением арматуры, соответствующем силе рас-
тяжения и передаваемым на бетон как усилие сжатия при изготовлении,
то растянутые элементы можно рассчитывать как сжатые с коэффициен-
том продольного изгиба
= 1.
Общий коэффициент использования прочности материалов для
фермы в целом определяется по формуле
¦
¦
n
i
i
n
i
ii
V
VK
K
1
1
о
, (32)
где
i
V
объем i-го элемента фермы, имеющей n элементов (i = 1, …, n).
Из формулы (31) следует, что чем ближе коэффициенты K
i
, K
o
к еди-
нице, тем полнее используется прочность материала фермы.
После подбора сечений элементов из условия прочности и устой-
чивости производят окончательный расчет фермы по второй группе пре-
дельных состояний по деформациям. Так, прогиб фермы в середине про-
лета не должен превышать установленной величины для нормальных
условий эксплуатации:
.
25
0
][
l
ff d
(33)
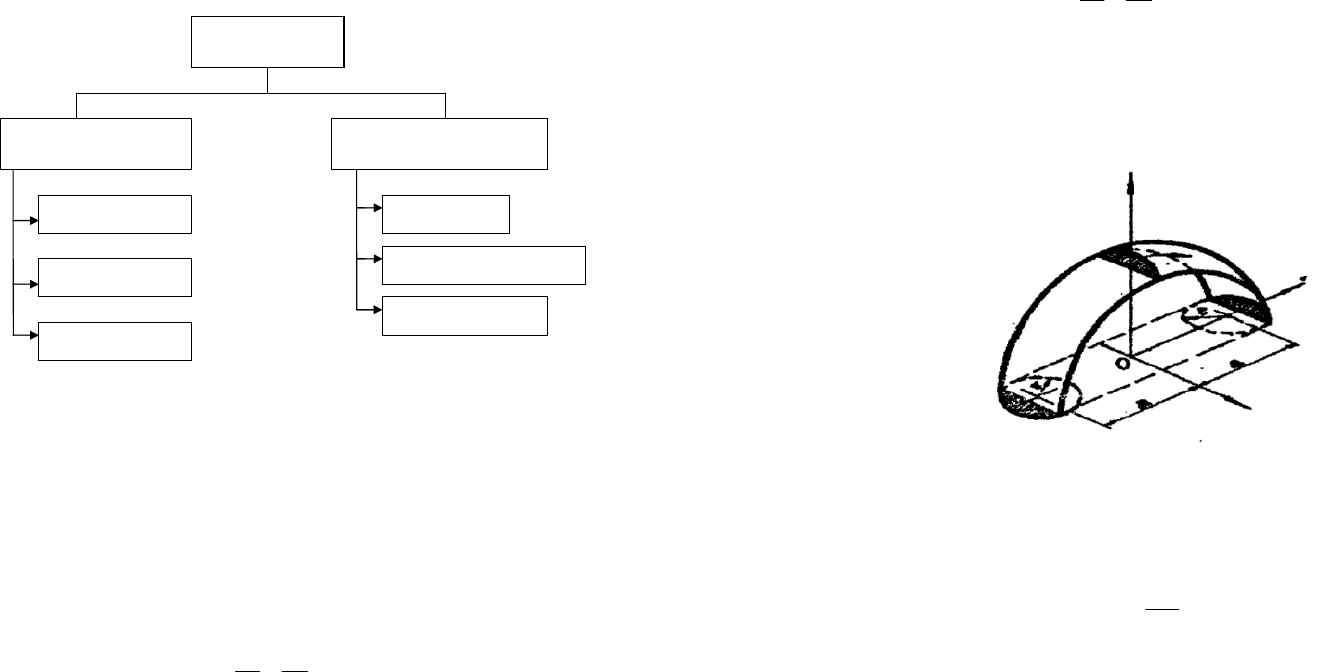
134 135
Проведенные расчеты для железобетонных ферм могут быть вы-
полнены и для ферм из других материалов, что позволит выбрать луч-
ший вариант по указанным ранее критериям.
Выполненные расчеты ферм из различных материалов, различной
конфигурации и высоты дают возможность по указанным ранее крите-
риям выбрать наилучший вариант.
4. Оптимизация железобетонной оболочки
Альтернативное ДЦ для выбора проектного
решения железобетон-
ной оболочки приведено на рис. 33.
Железобетонные
оболочки
Оболочки одинарной
кривизны
Оболочки двойной
кривизны
Цилиндрические
Параболические
Коноидальные
Сферические
Параболические своды
Гиперболические
Рис. 33. Разновидности оболочек
В программном комплексе SCAD оболочки можно строить как тела
вращения образующей с заданием радиусов вращения и центральных
углов для начальной и конечной точки оболочки, а также строить их по
формулам.
В качестве примера рассмотрим оболочку двойной кривизны –
бочарный (параболический) свод – построенный для плана 6ґ24 по
формуле
,/
12
–
3
–
22
k
yx
z
¸
¸
¹
·
¨
¨
©
§
(34)
где z, x, y – координаты точек оболочки с началом координат в верхней
точке и в центре площади (рис. 34); k – показатель стрелы подъема
(h/l = 1/2k).
В примере k = 4; h/l = 1/8, т. е. высота подъема оболочки h меньше
пролета l в 8 раз для обоих направлений.
При распределенной вертикальной нагрузке
q = 7 кН/м
2
и при на-
грузке от собственного веса тело оболочки свода в основном работает на
сжатие в двух направлениях. Оптимизацию оболочки в этом случае бу-
дем производить по объему потребного бетона на ее устройство при не-
котором отношении высоты подъема к пролету h/l:
формула оболочки
;4/)
1
2
3
(
22
yx
z
материал – бетон В25;
толщина –
мм;10050
min
G
нагрузка – собственный вес и
2
м/кН7 q
.
x
y
z
Рис. 34. Бочарный свод
Ус и ли е сжатия от распределенной нагрузки q в замке свода опреде-
ляется по формуле
.
8
2
h
qL
N
(35)
С уменьшением высоты свода h (рис. 35) увеличивается усилие N
и напряжение в сжатой оболочке, что требует увеличения ее толщины
для обеспечения условия прочности:
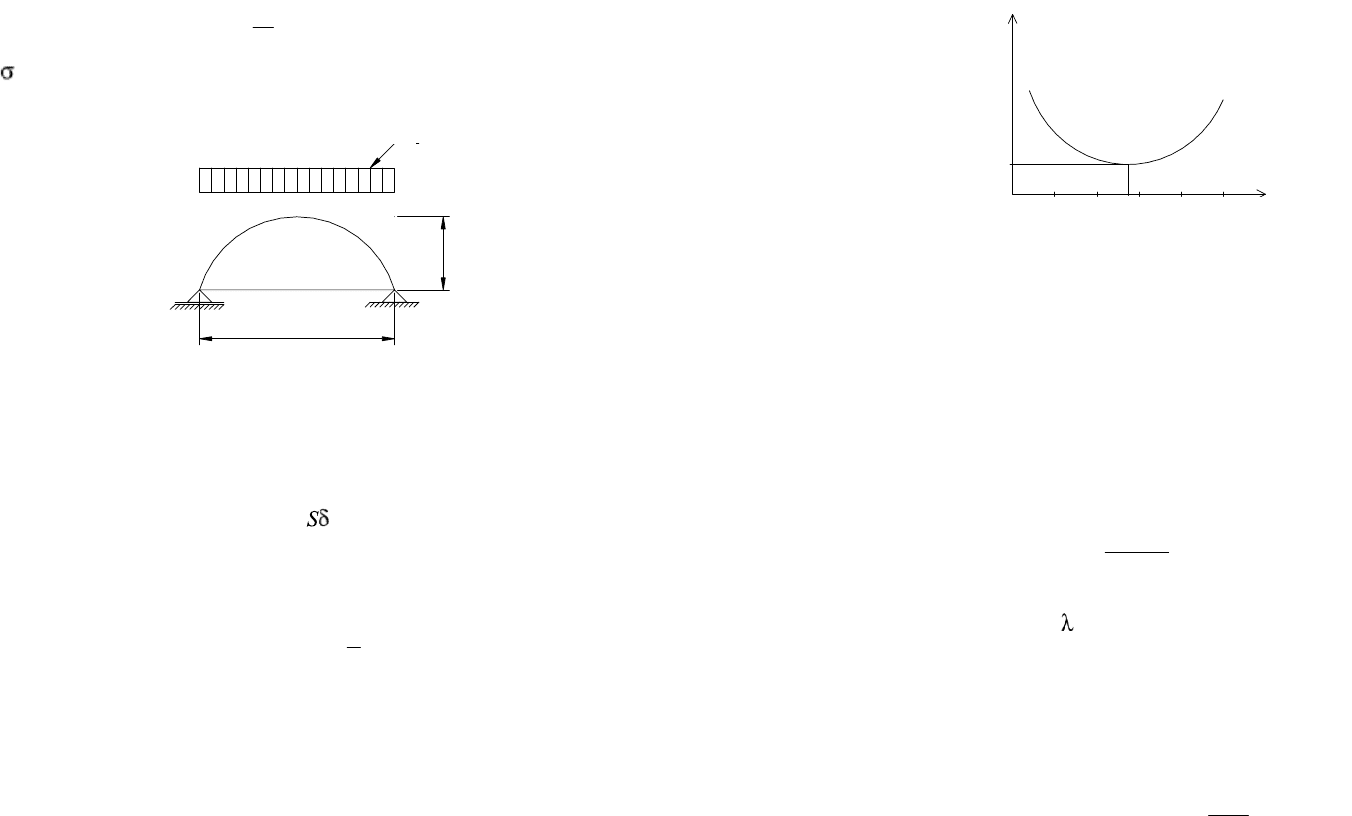
136 137
,
b
R
N
d
G
V
(36)
ãä å – напряжение сжатия от расчетной нагрузки; R
b
– расчетное
сопротивление бетона.
q
L
h
Рис. 35. Схема работы свода
Из формул (35) и (36) следует, что объем оболочки будет увеличи-
ваться с уменьшением стрелы подъема h. С другой стороны, объем обо-
лочки зависит от площади ее поверхности:
V =
, (37)
где S – площадь поверхности оболочки.
Для бочарного свода
,3,51
2
21
»
»
¼
º
«
«
¬
ª
¸
¹
·
¨
©
§
l
h
LLS
(38)
где L
1
и L
2
– пролеты оболочки в двух направлениях.
Зависимость объема оболочки от стрелы подъема h/l показана на
рис. 36. Минимальный расход бетона соответствует стреле 1/6…1/8 от
пролета l.
Это обстоятельство выявляется расчетом с использованием програм-
мы SCAD для оболочки, построенной по формуле (27) при разных зна-
чениях k. Заметим, что оболочки из технологических соображений сле-
дует принимать не менее 50
мм, в сборных ребристых оболочках – не
менее 30 мм.
При оптимизации оболочек арочного типа с затяжкой необходимо
также иметь в виду, что при малых значениях высоты h увеличивается
потребность стали на устройство затяжки.
V, м
3
V
мin
0,0 0,1 0,2 0,3 0,4 0,5
h/l = (1/2 k)
Рис. 36. Зависимость объема от стрелы
5. Проектирование ограждающих конструкций
Расчет ограждающих конструкций выполняется в целях обеспечения
необходимых для эксплуатации температурно-влажностных условий
внутри зданий. Толщина ограждающих конструкций определяется из
уравнения теплопроводности Фурье для потока теплоты
,
вн
At
b
TT
Q
O
(39)
где Q – количество теплоты;
– коэффициент теплопроводности материала
ограждения; Т
н
, Т
в
– температура снаружи и внутри здания; А – площадь
ограждения; t – время процесса теплопередачи; b – толщина ограждения.
Для здания, имеющего n ограждающих поверхностей, общее коли-
чество тепла, теряемого через ограждение, определяется по формуле
.
1
вно
¦
O
n
i
i
ii
b
A
tТТQ
Такое количество тепла должно поступать из системы отопления
для обеспечения нормальных условий эксплуатации здания.
Представляет интерес определение некоторой оптимальной толщи-
ны ограждения, соответствующую минимальной сумме стоимости его
устройства и затрат на отопление здания при эксплуатации.

138 139
Стоимость устройства ограждения
,CС
1
¦
n
i
miiim
bА
где
mi
С
– стоимость ограждения на i-м участке (i = 1, …, n) с
поверхностью А
i
и толщиной b
i
.
Затраты на отопление составляют величину
,CС
o QQ
Q
где
Q
C
– стоимость единицы теплоты с учетом устройства системы
отопления, ее эксплуатации и стоимости топлива.
Тогда математическую модель условия оптимальности можно за-
писать в таком виде
.minCC o
Qm
Z
(40)
Решение в замкнутом виде получим, рассматривая участок ограж-
дения площадью А = 1.
Стоимость устройства ограждения
mm
bCС
.
Затраты, обусловленные потерей тепла на этом участке,
.CС
вн
QQ
t
b
TT
O
Ус л о в и е оптимальности (40) получает вид
min,CC
2
1
o
b
k
bkZ
Qm
где k
1
=
Qm
tTTk C)(;C
вн2
O
– коэффициенты, определяемые по данным
статистики для заданного района строительства.
Зависимость целевой функции Z от толщины ограждения b показа-
на на рис. 37.
z
С
m
С
Q
С
m
С
Q
z
b
b
0
Рис. 37. Определение оптимальной толщины ограждения
Из условия
0
d
b
dz
находим оптимальную толщину ограждения
.C
C
вн
o Q
m
t
TT
b
O
(41)
В последние годы в Санкт-Петербурге проводится реконструкция
зданий с утеплением ограждающих поверхностей. Выяснилось, что
с увеличением цен на топливо целесообразно повысить сопротивление
теплопередаче стен за счет дополнительной теплоизоляции. Экономия
на материале стен при строительстве оказалась недальновидной, посколь-
ку затраты на отопление резко увеличились. Системный подход к пост-
роению критерия оптимальности с
учетом затрат не только на устрой-
ство ограждения, но и на отопление зданий, дает возможность испра-
вить создавшееся положение.
В свете изложенного представляет интерес устройство в Санкт-Пе-
тербурге зданий с вентилируемыми фасадами. Стены фасадов зданий
устраиваются слоистыми, включают вентилируемый зазор и слой специ-
альной теплоизоляции. Разность давлений в нижней и
верхней части зда-
ния создает тягу в вентиляционном зазоре, воздух в зазоре поднимается
вверх, в результате из ограждающей стены удаляется атмосферная и внут-
ренняя влага. Зимой такая конструкция защищает здание от потерь теп-
