Пеньковский Г.Ф. Основы информационных технологий и автоматизированного проектирования в строительстве

Подождите немного. Документ загружается.

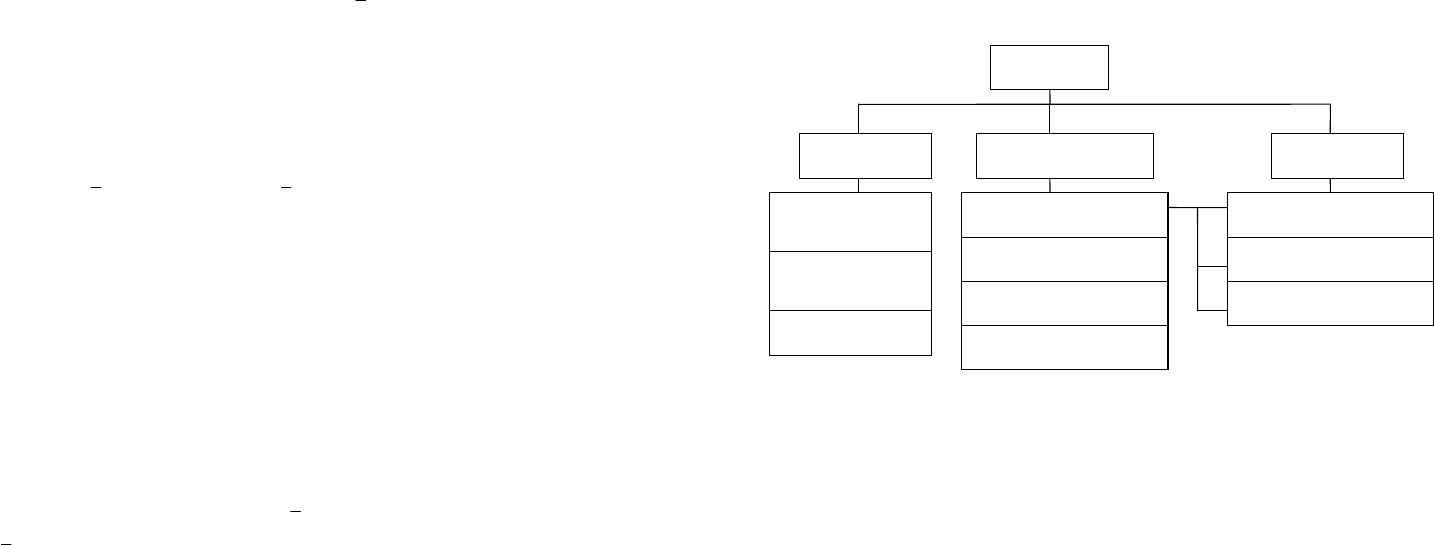
60 61

Кортежное представление модели (18), (19) отражает ее структуру,

но не содержит количественного описания связей между элементами.

Построение моделей и их использование для решения строительных про-

блем с получением количественных оценок рассмотрено далее.

4.2. Классификация моделей и требования к ним

Поскольку модели отражают основные свойства систем, то вид

модели тесно связан с видом моделируемых систем,

классификация ко-

торых приводилась ранее. При этом различают два больших класса мо-

делей, связанных с характером моделируемых систем – статические

и динамические модели.

Статические модели отражают структуру, вид объектов, состав их

элементов, образующих целостную систему.

Динамические модели создаются для моделирования процессов

в системах, протекающих в пространстве и во времени.

По материалам моделей, способам

построения и использования

различают следующие разновидности моделей (рис. 23).

Модели

Физические Аналитические Смешанные

Физически

подобные

Геометрически

подобные

Математические

Знаково-графические

Текстуальные

Эвристические

Детерминированные

Вероятностные

Имитационные

Аналоговые

Рис. 23. Разновидности моделей

Физические модели – модели из реальных материалов, построен-

ные с соблюдением законов подобия. Физические модели можно разде-

лить на физически подобные, геометрически подобные и аналоговые

модели.

Перечень основных свойств, которыми должна обладать модель

системы, определяется целью функционирования системы, характерис-

тиками и свойствами ее элементов, задачами исследования.

Упрощенное представление системы в модели имеет целью

упрос-

тить и сам процесс исследования, в котором должен решаться вполне

ограниченный круг задач, являющихся существенными именно в этом

исследовании. Степень соответствия (адекватности или подобия) моде-

ли и системы может быть различной. Естественно, что полное тожде-

ство модели и системы наилучшим образом решает все проблемы иссле-

дования, однако экономически такие модели

оказываются нецелесооб-

разны, а моделирование теряет свой смысл.

Понятие «моделирование» является более общим по отношению к

модели. В большинстве случаев моделированием называют процесс иссле-

дования системы на ее модели, включая и построение модели этой системы.

В соответствии с кортежным представлением системы (15) описа-

ние модели имеет вид



vvSytaxx ,,,,,,,:

, (18)

где



 Xx

– набор входных воздействий в систему (



– область вхо-о-

дов);



 Xx

– набор выходных воздействий;

Aa 

– набор постоян-

ных параметров системы;

Yy 

– набор переменных параметров;





taxSy ,,



– правило функции оператора S, включающее зависимость

от времени

Tt 

;





ytaxvx ,,,

– 

– правило v для области выходных

воздействий;





taxvx ,,

– 

– правило

, получаемое подстановкой фун-

кции S в правило v.

В практике моделирования часто используется модель системы типа

«черного ящика», содержание которого неизвестно, но известна одно-

значная связь между входом и выходом для определенных ситуаций.

Повседневными примерами таких систем являются телевизоры, прием-

ники. Подавляющему числу людей, пользующихся этими приборами, их

устройство неизвестно. Однако

это не мешает им получать изображение

и звук нужной интенсивности с помощью кнопок и регуляторов.

Кортеж для модели типа «черного ящика» имеет минимальное чис-

ло составляющих компонентов



vxx ,,:

(19)

где







xvx

62 63

материалов. Они могут быть математическими, знаково-графическими

или текстуальными моделями.

Математические модели представляют собой совокупность фор-

мул и логических условий, связывающих параметры состояния модели и

внешние воздействия. Разновидностями математической модели явля-

ются детерминированные, вероятностные (статистические или стохас-

тические) и имитационные модели.

Детерминированная математическая модель (линейная, нелинейная,

непрерывная, дискретная – по виду функций) однозначно

связывает вход-

ные и выходные параметры модели функциями соответствующего вида.

В вероятностной модели связи параметров носят случайный ха-

рактер, описываются законами теории вероятностей и математической

статистики.

Имитационная модель содержит детерминированные, вероятност-

ные и вообще четко не описанные связи. Чтобы получить представление

о результатах моделирования требуется многократное применение мо-

дели.

Знаково-графические

модели содержат знаки, символы, схемы, таб-

лицы, графики или чертежи, раскрывающие структуру системы и взаи-

мосвязи между элементами.

Текстуальные модели описывают свойства систем с помощью язы-

ковых текстов, таблиц, имеют вид инструкции, руководства и т. п.

Разновидностью аналитической модели является встречающаяся в

литературе эвристическая модель. Такая модель строится на основе ги-

потезы, научного предположения и интуиции исследователя. Примене-

ние эвристической модели нуждается в специальном обосновании дос-

товерности получаемых результатов моделирования.

Из всех аналитических моделей наиболее четкую формализацию

связей имеют математические модели. Знаково-графические модели об-

ладают большой наглядностью. Наибольшей сложностью в описании

связей между элементами отличаются текстуальные модели.

В практике моделирования часто используют

смешанные модели,

представляющие собой комбинации отдельных разновидностей физичес-

ких и аналитических моделей.

Независимо от вида модели все они должны отвечать следующим

требованиям.

1. Модель должна быть узконаправленной на достижение

конкретной цели исследования, максимально простой, отражать лишь те

Физически подобные модели создаются для изучения отдельных

физических явлений с соблюдением законов подобия для этих явлений

(механические, аэродинамические, гидравлические модели, модели теп-

лопередачи и т. п.). Например, для оценки несущей способности балок

реального покрытия здания можно использовать механическую модель

в виде балки уменьшенных размеров.

Геометрически подобные модели могут выполняться из самых раз-

личных материалов. Они отличаются от оригинала масштабом, и это

позволяет исследовать геометрическую структуру системы. Свойства

материала

модели здесь не имеют значения. Примерами таких моделей

могут служить макеты зданий, используемые при разработке архитек-

турных решений в застройке города.

Аналоговые модели построены с использованием аналогии в раз-

личных процессах, имеющих разную физическую природу, но одинако-

вые зависимости между некоторыми параметрами этих процессов.

Пусть механическое напряжение в центрально нагруженном стер-

жне определяется по формуле

, (20)

где N – продольная сила; A – площадь сечения стержня.

Аналогично определяется сила тока в проводнике по закону Ома:

, (21)

где U – электрическое напряжение; R – сопротивление проводника

Зависимости (20) и (21) дают возможность исследовать механичес-

кие напряжения с помощью электрической схемы, т. е. системы, имею-

щей совершенно другую физическую природу.

При построении аналоговых моделей для решения задач, связан-

ных с распределением ресурсов, могут использоваться также гидравли-

ческие, оптические, акустические, тепловые модели. Построение и

при-

менение таких моделей ждет своих исследователей.

Аналитические (абстрактные) модели построены человеком на ос-

нове наблюдения за окружающей природой без привлечения реальных

64 65

делирование дает возможность оценить адекватность модели и системы

наилучшим образом.

Прототип

Физические

модели

Физический

эксперимент

Математичес-

кая модель

Математическое

моделирование

Теория по

оби

Теория размерностей

Рис. 24. Схема взаимосвязи физической и математической моделей

Физическое моделирование может быть использовано непосред-

ственно для проектирования и управления в строительстве. Примером

этому является широкое применение макетирования в архитектурном

проектировании городской застройки. В Киевском инженерно-строитель-

ном институте физическая модель фундамента сложной конфигурации ус-

пешно применялась для расчета и проектирования конструкций реального

сооружения. Теоретическое решение контактной задачи для такого фунда-

мента просто неизвестно. Однако измерение деформаций и контактных дав-

лений на физической модели дали возможность, используя теорию подо-

бия, определить усилия и деформации для реального фундамента.

Тесная связь физического и математического моделирования сис-

тем делает необходимым краткое изложение основных положений тео-

рии подобия и теории размерностей, на базе которых осуществляется

физическое

моделирование.

Теория подобия изучает условия, в которых процессы (объекты)

можно полагать подобными друг другу. Два процесса называют физи-

чески подобными, если они имеют одинаковую физическую природу

и их характеристики отличаются только масштабом для одноименных

параметров. При этом масштабы эти не могут быть произвольными, они дол-

жны отвечать требованиям, изложенным в соответствующих теоремах

[8].

Известны три основных теоремы подобия.

Теорема 1. Коэффициенты подобия (масштабы) параметров моде-

ли и системы должны соотноситься между собой согласно физическому

закону, составляющему предмет исследования на данной модели.

свойства системы, которые влияют на конечные цели функционирования

этой системы в данном исследовании.

2. По набору свойств модель должна быть адекватна системе.

В ней должны

выполняться основные физические законы, которые про-

являются в реальной системе.

3. Сложность модели, ее структура должны быть оптимальными

и достаточными для обеспечения необходимой точности результатов мо-

делирования. Чувствительность модели к изменению параметров долж-

на удовлетворять заданным требованиям по точности.

4. Модель должна быть экономичной по затратам всех видов ре-

сурсов в процессе

моделирования.

Отметим здесь противоречивость различных требований, обуслов-

ленных, с одной стороны, стремлением максимально упростить модель,

с другой – получить модель, адекватную системе и достаточно полно

отражающую ее свойства. Поэтому построение модели с учетом всех

требований является искусством исследователя и приходит с опытом.

Основным и обобщающим требованием к моделям и процессу мо-

делирования

является обеспечение высокой достоверности и надежнос-

ти результатов исследований при моделировании систем.

4.3. Физическое моделирование систем.

Теории подобия и размерностей

Физическое моделирование применяется обычно в эксперименталь-

ных исследованиях для обоснования теоретических предпосылок, науч-

ных гипотез, которые впоследствии становятся основой для разработки

математических моделей. На рис. 24 показана схема разработки матема-

тической модели для

некоторого физического прототипа.

Для моделирования процесса или объекта исследователь находит

в окружающей природе ближайший прототип со сходным процессом,

дополняет его своими представлениями, строит физическую модель

с учетом требований теории подобия и теории размерностей. Затем, прове-

дя физический эксперимент, получает материал для теоретических обоб-

щений, которые и дают возможность построить математическую модель.

Такова

общая закономерность построения математических моделей.

В отдельных случаях авторы могут строить свои математические

модели на результатах аналогичных исследований, проведенных в смеж-

ных отраслях науки и техники. Однако и в этих случаях физическое мо-

66 67

Теорема 2. При моделировании необходимо обрабатывать не от-

дельные параметры, а их комплексы, входящие в критерий подобия.

Теорема 3. Процессы в модели и системе должны описываться од-

ними и теми же уравнениями, граничными и начальными условиями.

Теория размерностей изучает законы построения моделей на ос-

нове анализа размерностей параметров объектов исследования.

Теоремы теории размерностей

Теорема 1. Размерности параметров модели и системы должны быть

одинаковыми.

Теорема 2 (теорема Фурье). В любом уравнении все его члены дол-

жны иметь одинаковую размерность.

Теорема 3 (

-теорема). Любой параметр в модели и системе с помо-

щью преобразований и некоторого

числа можно представить в безраз-

мерном виде.

При проведении физических экспериментов кроме проблемы по-

добия необходимо иметь в виду еще одну особенность моделирования.

Дело в том, что все реальные системы, процессы и их параметры имеют

вероятностную природу, обладают различной изменчивостью при изме-

рениях. Поэтому данные измерений в экспериментах должны быть дос

таточно представительны по выборке и обработка их должна произво-

диться методами математической статистики.

Указанные обстоятельства свидетельствуют о том, что физическое

моделирование является достаточно сложным делом, а авторам экспери-

ментов всегда предстоит серьезная работа по доказательству пригоднос-

ти полученных на модели результатов для реальной системы.

4.4. Математическое моделирование систем

Математическое моделирование систем является

наиболее эконо-

мичным и эффективным способом получения прогноза состояния сис-

тем при обосновании решений. В п. 4.3 была изложена общая законо-

мерность построения математических моделей, их связь с физическим

моделированием. После выбора прототипа объекта (процесса), выбора

математического аппарата для формализации связей в модели и обеспе-

чения всех требований к моделям проводится численный

эксперимент

обычно с широким применением вычислительной техники.

Например, для механического взаимодействия тел физическим

законом является второй закон Ньютона

F = ma, (22)

где F – сила, действующая на массу тела m; a – ускорение, получаемое

массой в результате действия этой силы.

Если t – время действия силы, S – путь движения массы, то

(23)

Из выражения (23) получим критерий подобия по Ньютону

Ne =

= idem. (24)

Критерий подобия, записанный через коэффициенты подобия,

называется индикатором подобия

,(25)

где

– коэффициент подобия для линейных размеров модели и систе-

мы;

– коэффициент подобия для масс;

– коэффициент подобия для

времени протекания процесса в модели и в системе;

– коэффициент

подобия для сил.

Аналогичным образом записываются критерии и индикаторы по-

добия в исследованиях действия гравитационных сил (критерий Фруда),

волновых явлений (критерий Эйлера), явлений теплопроводности (кри-

терий Фурье) и другие.

Отметим, что невозможно обеспечить подобие физической модели

и системы по всем критериям. В зависимости от физики изучаемых яв-

лений значение индикатора

подобия будет говорить о степени подобия

модели и системы. Чем ближе его значение к единице, тем точнее моде-

лирование.

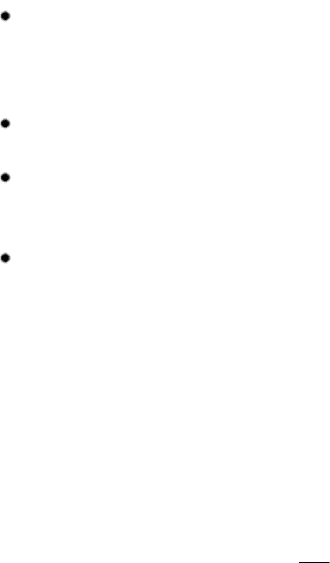
68 69

В строительной механике широкое применение получили числен-

ные методы расчета на основе теории матриц. С помощью ЭВМ стало

возможным решение уравнений метода сил и метода перемещений с боль-

шим числом неизвестных.

Для расчета конструкций в сооружениях сложной конфигурации

получили развитие численные методы на основе дискретных в простран-

стве и во времени расчетных

схем – метод конечных разностей (МКР),

метод конечных элементов (МКЭ), дискретно-шаговые методы (ДШМ).

Основная идея МКР состоит в замене точных значений производ-

ных их приближенными значениями через конечные разности функций.

Замена точных значений производных конечными разностями сво-

дит задачи, описываемые системами дифференциальных уравнений,

к задачам решения систем алгебраических уравнений в

рекуррентной

форме, что очень удобно для вычисления на ЭВМ.

В МКЭ объект расчета заменяется системой плоских или простран-

ственных конечных элементов, а математическая модель (уравнения рав-

новесия, совместности деформаций и закона деформирования элемен-

тов) в канонической форме описывает взаимодействие элементов в со-

оружении с учетом граничных условий. Совместное решение уравнений

математической модели

для всех конечных элементов раскрывает напря-

женно-деформированное состояние сооружения.

Дискретно-шаговые методы описывают состояние объекта в МКР

или МКЭ в последовательных дискретных шагах расчета от начала заг-

ружения. Это дает возможность достаточно просто учитывать нелиней-

ные свойства материалов конструкций и внешних воздействий путем

аппроксимации нелинейных функций кусочно-линейными с любой

за-

данной точностью приближения.

Математическое моделирование является главной составной час-

тью математического обеспечения систем автоматизированного проек-

тирования и управления (САПР и АСУ), которое содержит описание ма-

тематических методов, алгоритмы и модели для решения задач.

На рис. 25 показана схема функционирования САПР и АСУ, пояс-

няющая роль математического моделирования при обосновании прини-

маемых

решений.

Пользователь САПР и АСУ (оператор) вводит исходные данные

в блок 1. В блоке 2 хранится информация базы данных, которая в конк-

ретном исследовании является неизменной. Это требования нормативов,

инструкций, положения рекомендаций, носящие общий характер. Опе-

Очень важным этапом в подготовке к моделированию является оцен-

ка адекватности математической модели и системы. Известны следую

щие способы оценки адекватности.

Анализ структуры математической модели (ММ), полноты опи-

сания функциональных связей системы, ограничений на значение отдель-

ных параметров. Такой анализ дает возможность исключить грубые ошиб-

ки в модели еще до процесса исследования.

Анализ работоспособности ММ в ситуациях, когда результаты

моделирования очевидны.

Решение тестовых примеров, сравнение результатов моделиро-

вания на построенных ММ с результатами, полученными другими авто-

рами и на других моделях при одинаковых исходных условиях.

Проверка данных моделирования экспериментальным путем на

физических моделях.

Оценка адекватности модели и системы предполагает их соответ-

ствие друг другу по чувствительности реагирования на изменение вход-

ных параметров. Количественно чувствительность модели выражается

изменением выходных параметров при некотором единичном изменении

одного из входных параметров. Изменения могут быть в абсолютных

единицах измерения, они могут быть относительными

– в долях едини-

цы или в процентах. Количественное представление о чувствительности

модели к изменению параметра x дает частная производная по x

где Ф – функция изменения состояния модели, отражающая изменение

выходных параметров.

Построение ММ заканчивается, если удовлетворены все требова-

ния, предъявляемые к модели, проверена ее работоспособность и чув-

ствительность. Далее ММ могут быть использованы для оценки состоя-

ния систем аналитическим или численным методом путем проведения

численного эксперимента на ЭВМ. С появлением вычислительной тех-

ники

интенсивно развиваются численные методы как раздел приклад-

ной математики. Численными методами решаются типичные задачи ма-

тематического анализа (приближение, аппроксимация, дифференциро-

вание, интегрирование), задачи алгебры, осуществляется решение диф-

ференциальных и интегральных уравнений, задач оптимизации.

70 71

S = dE, (26)

где S – напряжение сжатия или растяжения в стержне; d – относительная

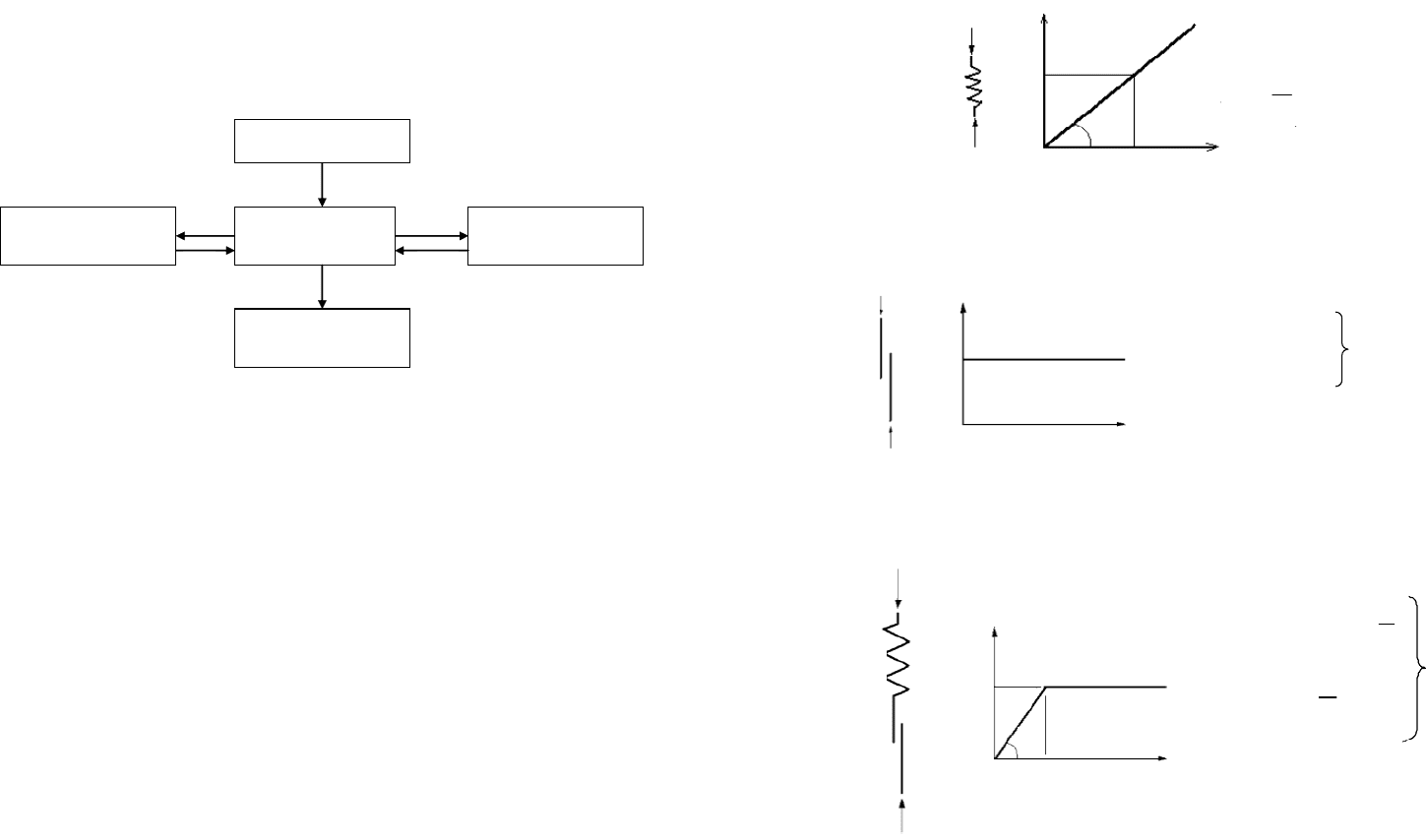
деформация стержня; E – модуль упругости (модуль Юнга).

На рис. 26 показана графическая связь S и d в модели Гука.

Рис. 26. Модель Гука

Для стержня из идеально пластического материала применяется

модель Сен-Венана (рис. 27).

при

, d = 0

при S = K, d of

Рис. 27. Модель Сен-Венана

Деформации упруго-пластического стержня описываются моделью

Прандтля (рис. 28).

S = K

при S < K, S = dE;

при S = K, d of

Рис. 28. Модель Прандтля

рационный блок 3 (процессор) осуществляет моделирование по соответ-

ствующей программе, используя информацию из блоков 1 и 2. Блок при-

нятия решений 4 контролирует состояние моделируемой системы по за-

данным критериям с учетом заданных ограничений и дает команду на

окончание процесса моделирования, после чего информация о принятом

решении и соответствующем ему состоянии подается на выходной блок

5 на

экран дисплейного терминала или в виде распечатки на АЦПУ.

Пользователь ЭВМ анализирует эту информацию и, если решение его не

устраивает, меняет входные данные и процесс повторяется.

1. Входной блок

3. Операционный

блок

2. Блок хранения

информации

4. Блок принятия

решения

5. Выходной блок

(решения)

Рис. 25. Схема функционирования САПР и АСУ

Различие в математическом моделировании систем при проектиро-

вании и управлении состоит в том, что целью моделирования в первом

случае является разработка проектно-сметной документации на объект,

а во втором случае моделируются технологические процессы по возве-

дению этого объекта. При безбумажной технологии с общей информа-

ционной базой для САПР и АСУ моделирование

при проектировании

объекта непрерывно переходит в моделирование технологии производ-

ства работ, и процесс моделирования становится единым для всего со-

здаваемого объекта.

4.5. Реологические модели в строительстве

Реологические модели применяются для описания процессов де-

формирования конструкций в пространстве и во времени. Наиболее про-

стой и часто применяемой является модель Гука для идеально упругого

стержня

, в которой напряжения и деформации связаны зависимостью

72 73

ний от относительной деформации становится нелинейной. При разгрузке

в конструкциях появляются остаточные деформации.

Модель Прандтля применяют для учета деформаций в арматурных

стержнях из сталей с выраженной площадкой текучести.

Модель Фойгта используется в ди-

намических расчетах стальных и желе-

зобетонных конструкций, в которых вяз-

кость материала способствует затуха-

нию колебаний.

В качестве примера

использования

моделей рассмотрим работу простейшей

конструкции – железобетонного кронш-

тейна (рис. 31).

В верхнем стержне на растяжение

работают два стержня арматуры Ø12 мм

класса АIII. Подкос из бетона класса В20,

имеет сечение 300

300 мм. Требуется

отследить напряженно-деформированное состояние кронштейна от воз-

растающей силы P вплоть до его разрушения.

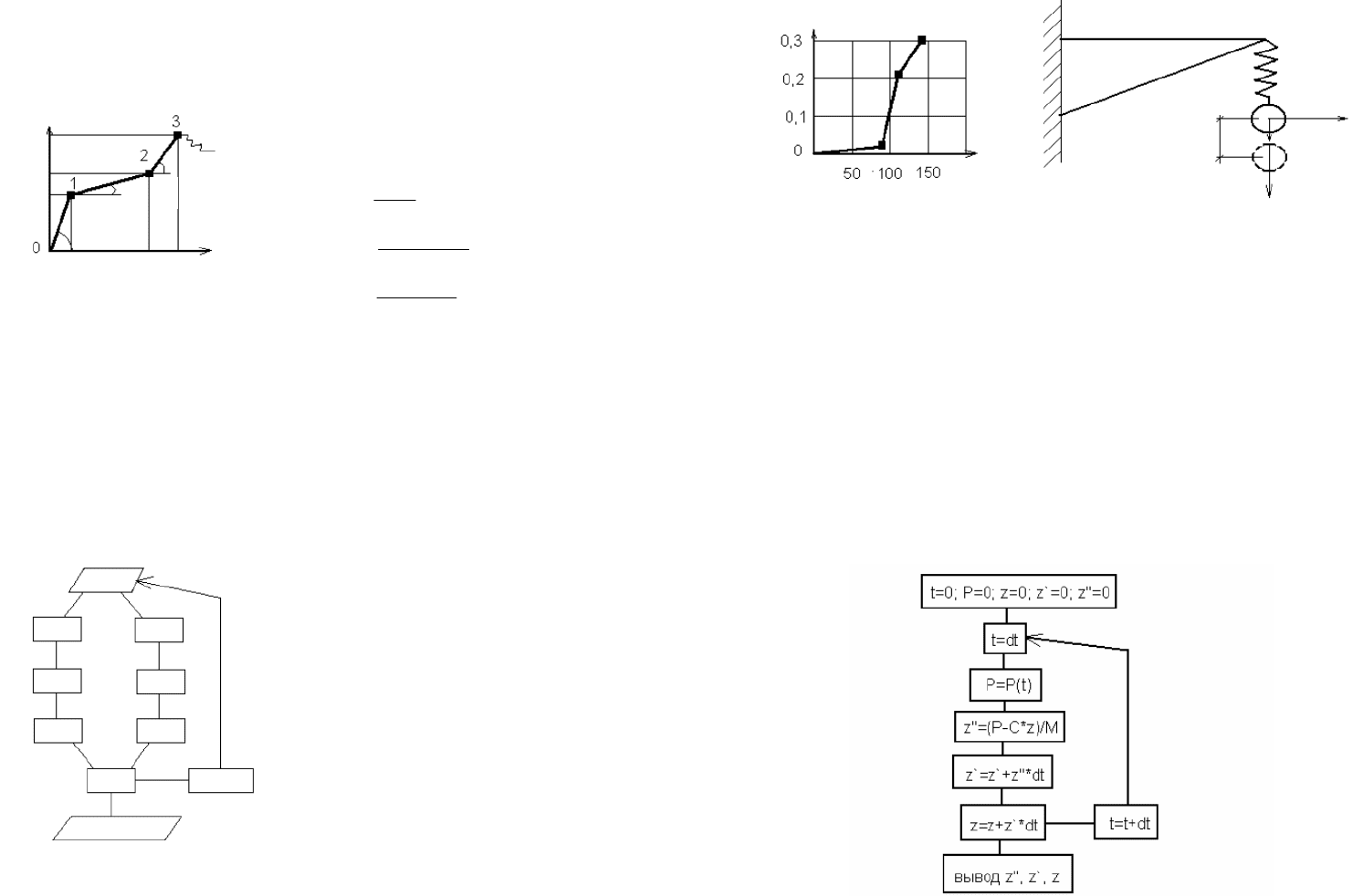
Диаграмма сжатия S(d) для бетона класса В20 показана на рис. 32.

Нелинейную диаграмму сжатия S(d) будем аппроксимировать ку-

сочно-линейной функцией с точками перелома 1, 2 и 3.

Рис. 32. Диаграмма сжатия бетона

класса В20

Координаты точек

ерелома:

5,7

S МПа, 0003,0

d ;

S МПа, 001,0

d ;

S МПа, 002,0

d (разрушение);

00025

0003,0

5,7

с1

E МПа;

0003,0001,0

5,713

с2



D E =

= 7857 МПа;

001,0002,0

1315

с3



D E =

= 2000 МПа.

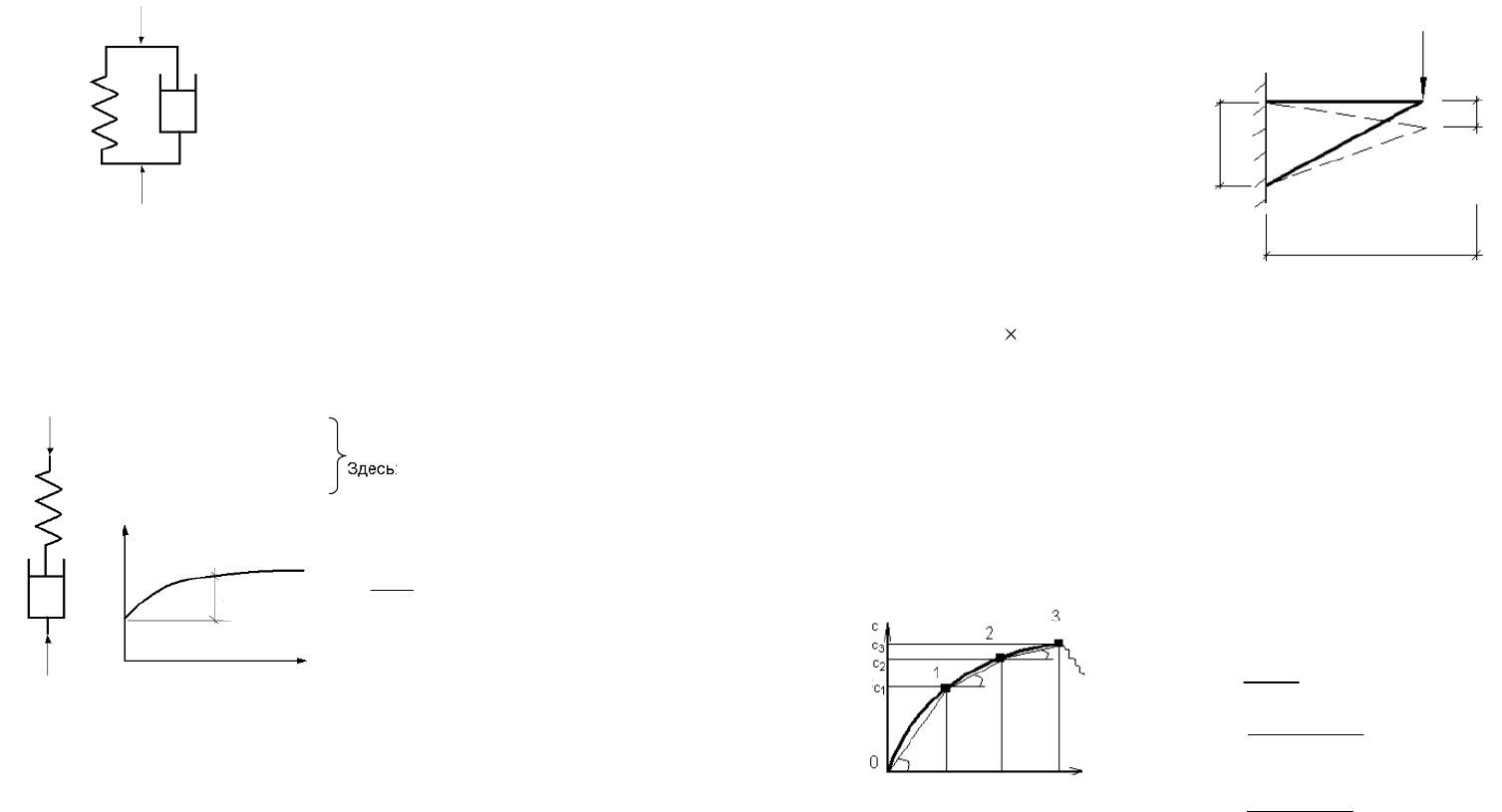
Модель Фойгта применяется для стержня из упруго-вязкого мате-

риала (рис. 29). Модель представляет собой комбинацию упругой моде-

ли Гука и вязкой модели Максвелла.

S = dE + dP

P – коэффициент вязкости материала;

d – скорость относительной

деформации

Рис. 29. Модель Фойгта

Для описания деформации материалов, обладающих свойством

ползучести, с развитием деформаций под нагрузкой во времени, приме-

няется модель технической теории ползучести старения (рис. 30).

(t) = d

d(t) = d

+ d

(t) = d

(1 + M

)

(t) – деформация ползучести

к моменту времени t;

– начальная (упругая) деформация;

)(

= характеристика

(t)

Рис. 30. Модель технической теории ползучести

Модель Гука применяется для оценки деформаций в различных кон-

струкциях, если напряжения в них не превышают половины предельных

напряжений, при которых происходит разрушение материала конструк-

ции. С увеличением напряжений выше половины предельных в конст-

рукциях развиваются пластические деформации; зависимость напряже-

Рис. 31. Схема кронштейна

ползучести

74 75

(

)

(

)

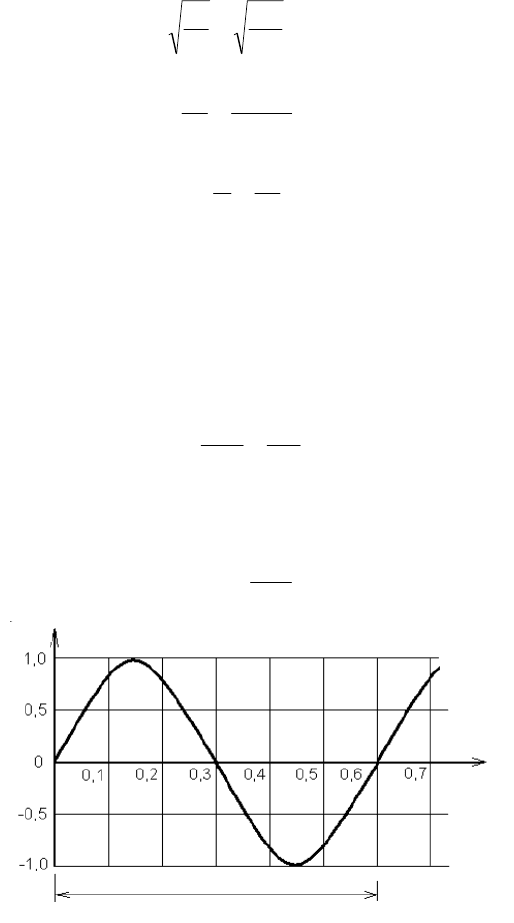
Рис. 36. Схема подвески массы М

Уравнение движения массы М имеет вид

  

0 

 CtzMtztP

, (27)

где P(t) – динамическая нагрузка, приложенная к массе М, находящейся

в равновесии; С – жесткость пружины в подвеске;

 



tztz ,

переме-

щение и ускорение массы М в момент времени t.

Из уравнения движения (27) дискретно-шаговым методом находятся

параметры движения массы М. Алгоритм вычисления приведен на рис. 37.

Рис. 37. Алгоритм вычислений параметров движения

Диаграмма растяжения для арматуры класса АIII показана на рис. 33.

Рис. 33. Диаграмма растяжения

арматуры класса АIII

400

МПа;

002,0

450

МПа;

07,0

600

МПа;

10,0

(разрушение).

000200

002,0

400

МПа;



002,007,0

400450

2 p

735 МПа;

500

07,010,0

450600



МПа.

Для оценки напряженно-деформированного состояния (НДС) крон-

штейна от возрастающей нагрузки используется дискретно-шаговый

метод расчета с алгоритмом, показанным на рис. 34.

Ус и ли я сжатия N

и растяжения N

определяются методом выреза-

ния узлов в кронштейне. Затем определяются напряжения в сжатом

и растянутом элементах, деформации с учетом диаграмм сжатия и растя-

жения. По этим деформациям определяется вертикальное перемещение

точки приложения силы f(p).

Для кронштейна с размера-

ми l = 3 м, h = 3 м разрушение про-

исходит при нагрузке P = 135 кН;

перемещение f

= 0,3 м. Первым

разрушается растянутый стер-

жень.

Диаграмма деформирования

кронштейна, полученная с помо-

щью электронных таблиц Excel,

показана на рис. 35.

Рассмотрим далее примене-

ние модели Гука в динамической

задаче о колебаниях массы М на

упругой подвеске (рис. 36).

Рис. 34. Алгоритм расчета НДС

c S

(p)

Вывод P, f

Рис. 35. Диаграмма деформирования

кронштейна

f, м

P, кН

76 77

Рекомендуемая литература к разделу I

1. Антонов А. В. Информация: восприятие и понимание. – Киев:

Наукова думка, 1988. – 184 с.

2. Варламов Н. В. Системы автоматизированного проектирования

в строительстве / СПбГАСУ. – СПб, 1992.

3. Голдман С. Теория информации / Пер. с англ. – М., 1957. – 446 с.

4. Информатика: учебник / Под ред. проф. Н. В. Макаровой. – М.:

Финансы и статистика., 1997. – 768 с.

5. Колесник

В. Д., Полтырев Г. Ш. Курс теории информации. – М.:

Наука, 1982. – 416 с.

6. Козырев А. А. Информатика: учебник для вузов. – СПб., 2002. –

511 с.

7. Орлов В. А., Филиппов Л. И. Теория информации в упражнениях

и задачах. – М.: Высшая школа, 1976. – 136 с.

8. Пеньковский Г. Ф. Системный анализ и моделирование систем в

строительстве / СПбГАСУ. –

СПб., 1999. – 97 с.

9. Информационные системы для руководителей / Ф. И. Перегудов

и др. – М.: Финансы и статистика, 1989. – 176 с.

10. Справочник библиографа / Науч. ред. А. Ванеев и др. – СПб.:

Профессия, 2003. – 560 с.

11. Технологические правила проектирования объектов строитель-

ства: методическое руководство. – М.: ГП УНС, 1998. – 127 с.

12. Ханенко В. Н. Информационные системы. – Л.: Машинострое-

ние, 1988. – 127 с.

13. Шеннон К. Э. Работы по теории информации и кибернетики /

Пер. с англ. – М., 1963. – 829 с.

14. Дворкина М. Я. Информационное обслуживание. Социокультур-

ный подход. – М.: НПО «Профиздат», 2003. – 112 с.

15. Информатика. Базовый курс / С. В. Симонович и др. – СПб.:

Питер, 1999. – 640 с.

Для системы с массой М = 1 кг с

/см, с жесткостью С = 100 кг/см

теоретическое значение круговой частоты колебаний

100

рад/с.

Частота колебаний

6,1

14,32



Гц.

Период собственных колебаний

63,0

6,1

На рис. 38 приведен график колебаний массы М, полученный с по-

мощью электронных таблиц Excel дискретно-шаговым методом по алго-

ритму на рис. 37 при dt = 0,1 c после воздействия на массу импульса

силы P = 100 кг длительностью 0,1 с.

При шаге dt = 0,1 / 2 = 0,05 c график практически не изменяется, что

доказывает устойчивость и достаточную

точность вычислений по Рунге –

Кутту. Статическое перемещение массы от максимальной нагрузки

100

max

ст

cм.

Максимальное динамическое смещение

max

= 1 см.

Коэффициент динамичности

ст

max

дин

, с

Рис. 38. График колебаний массы М

с.

78 79

ниями строительных норм. Затем производится ввод объекта в эксплуа-

тацию. На этапе строительства проектная организация осуществляет ав-

торский надзор за проведением строительных работ.

Эксплуатация объекта обеспечивает достижение целей инвести-

рования, вложенные средства окупаются к заданному сроку и объект

приносит запланированную прибыль инвестору. К моменту физичес-

кого или морального износа объект может

быть ликвидирован с ути-

лизацией его конструкций и оборудования, либо перепрофилирован

под новый технологический процесс. В последнем случае проектно-

изыскательская организация производит обследование состояния

объекта, разрабатывает проект капитального ремонта или проект рас-

ширения, реконструкции и технологического перевооружения основ-

ных фондов предприятия.

1.2. Порядок разработки и состав проектной документации

Порядок разработки и состав проектной

документации изложены

в строительных правилах СП 11-101–95 [22].

Разработка проектной документации на строительство объектов

осуществляется на основе утвержденных обоснований инвестиций

в строительство этих объектов.

Основным проектным документом на строительство является

технико-экономическое обоснование – проект – первая стадия разработки

проектной документации (рис. 1).

В одну стадию проект разрабатывается для простых типовых

объектов или объектов, строящихся по документации повторного

применения

. Производится привязка проекта к местным условиям,

согласование, экспертиза, утверждение и выдача проекта. Для уникальных

сооружений проект является первой стадией разработки документации,

а после его утверждения на второй стадии разрабатывается рабочая

документация.

Информационная технология проектирования представляет собой

процесс создания прогностической информационной модели объекта

будущего строительства (нового или реконструируемого). Проект, как

информационная модель объекта строительства

, разрабатывается в виде

технической документации, имеющей определенную структуру, форму

и содержание.

II. АВТОМАТИЗИРОВАННОЕ ПРОЕКТИРОВАНИЕ ОБЪЕКТОВ

СТРОИТЕЛЬСТВА

1. Общие положения проектирования объектов строительства

1.1. Инвестиционный проект в строительстве, его этапы

Инвестиционный проект в строительстве представляет собой план

вложения финансовых средств и материальных ресурсов в производство

на строительных предприятиях для достижения некоторых экономичес-

ких или политических целей. Порядок

вложения инвестиций в строи-

тельстве описывается в строительных правилах СП 11-11–95 [23], пре-

дусматривающих поэтапное развитие инвестиционного процесса. Основ-

ными являются три этапа этого процесса – замысел, реализация строи-

тельства и эксплуатация объекта [26].

Замысел инвестиционного проекта – это определение цели инвес-

тирования, номенклатуры проектируемой к выпуску продукции, назна-

чения и мощности объекта строительства. Для

этого изучается рынок

предполагаемой продукции, источники финансирования, возможности

достижения поставленной цели. Эту работу выполняет потенциальный

инвестор с привлечением консультантов на договорной основе и затем

разрабатывает ходатайство (декларацию) о намерениях инвестирова-

ния. После согласования декларации с местной администрацией пред-

полагаемого района размещения объекта инвестор совместно с проек-

тно-изыскательской организацией разрабатывает детальное обоснова-

ние

инвестиций в строительство объекта – бизнес-план строительства,

необходимый для получения кредита и открытия финансирования стро-

ительства.

Реализация строительства включает в себя разработку проектной

документации на объект. Вначале разрабатывается проект (утверждае-

мая часть рабочего проекта), производится согласование, экспертиза

и утверждение документации, выделяется участок под строительство

объекта. Затем разрабатывается рабочая документация со всеми специ

фикациями на материалы и оборудование, с объектной сметой на строи-

тельство. Готовится тендерная документация для конкурсного отбора

строительного подрядчика, который осуществляет строительство объек-

та в соответствии с утвержденной проектной документацией, требова-