Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials

Подождите немного. Документ загружается.

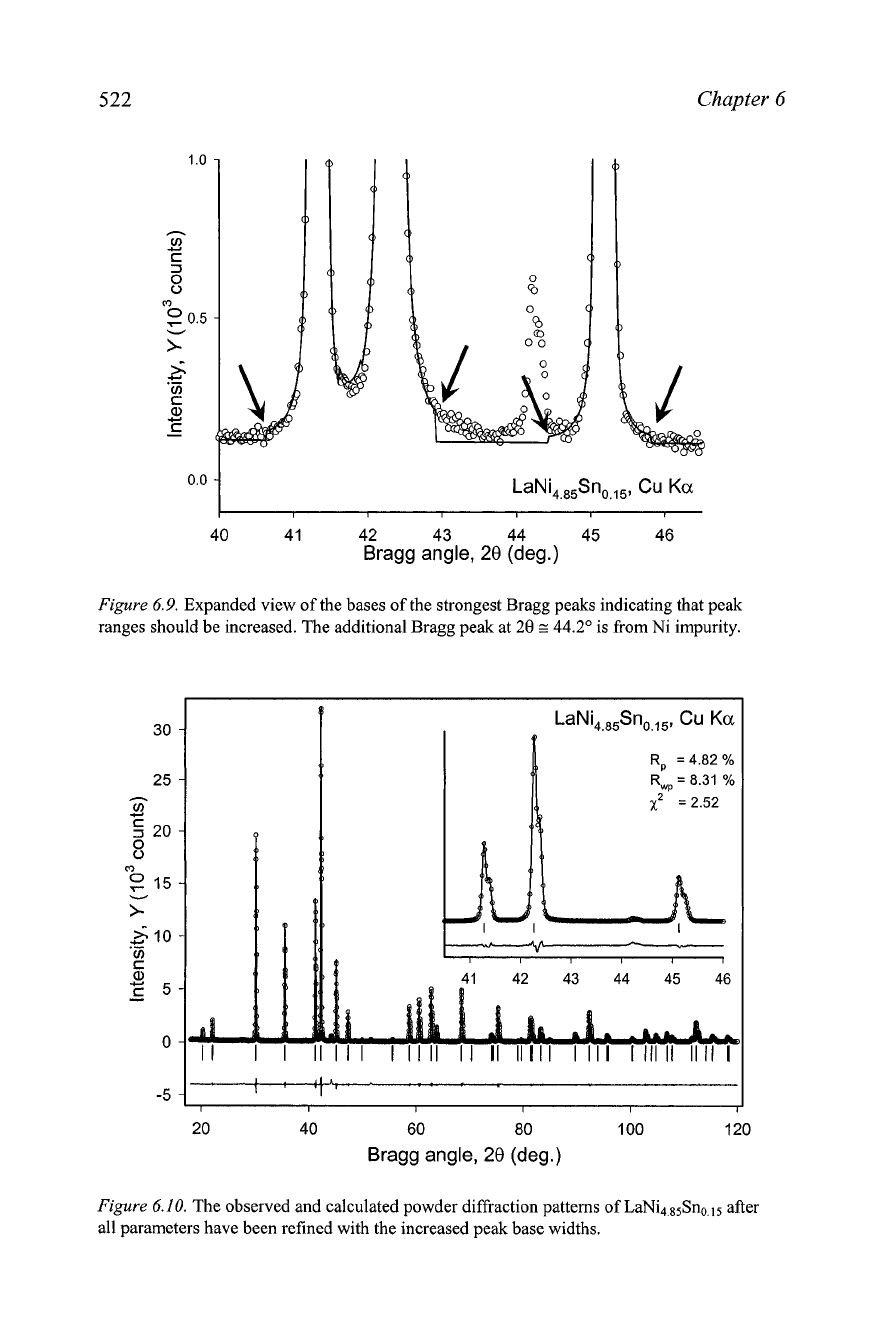
522

Chapter

0.0

LaNi

,,,,

,,,,,

40 4 1 42

44 45 46

Bragg angle, 28 (deg.)

Figure

6.9.

Expanded view of the bases of the strongest Bragg peaks indicating that peak

ranges should be increased. The additional Bragg peak at

44.2'

is from Ni impurity.

20 40 60 80 100 120

Bragg angle, 28 (deg.)

Figure

6.10.

The observed and calculated powder diffraction patterns of LaNi4,85Sno,,5 after

all parameters have been refined with the increased peak base widths.

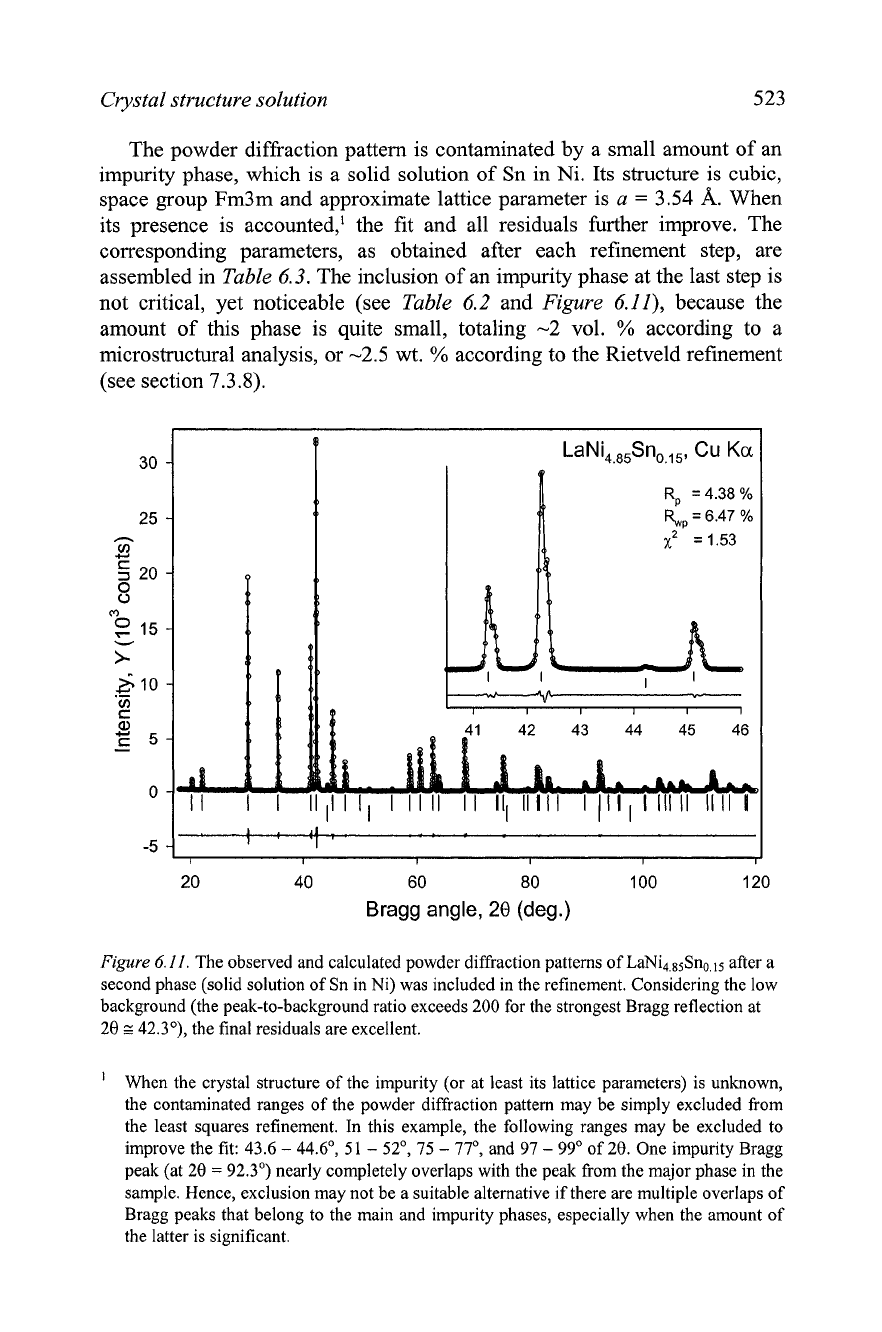
Crystal structure solution

523

The powder diffraction pattern is contaminated by a small amount of an

impurity phase, which is a solid solution of Sn in Ni. Its structure is cubic,

space group Fm3m and approximate lattice parameter is

3.54

When

its presence is accounted,' the fit and all residuals further improve. The

corresponding parameters, as obtained after each refinement step, are

assembled in

Table

6.3. The inclusion of an impurity phase at the last step is

not critical, yet noticeable (see

Table

6.2

and

Figure

6.11), because the

amount of this phase is quite small, totaling

-2

vol.

according to a

microshuctural analysis, or -2.5

wt.

according to the Rietveld refinement

(see section

7.3.8).

LaNi

,,,,

,,,,,

ll I I

1111

l1 I

II Ill

11111

I (Ill

IIIII

1111

60 80 100 120

Bragg angle,

(deg.)

Figure

6.11.

The observed and calculated powder diffraction patterns of LaNi4,85Sno.15 after a

second phase (solid solution of Sn in Ni) was included in the refinement. Considering the low

background (the peak-to-background ratio exceeds 200 for the strongest Bragg reflection at

42.3"), the final residuals are excellent.

When the crystal structure of the impurity (or at least its lattice parameters) is unknown,

the contaminated ranges of the powder diffraction pattern may be simply excluded from

the least squares refinement. In this example, the following ranges may be excluded to

improve the fit: 43.6

44.6', 51

52', 75

77", and 97

99" of 28. One impurity Bragg

peak (at 28

92.3') nearly completely overlaps with the peak from the major phase in the

sample. Hence, exclusion may not be a suitable alternative if there are multiple overlaps of

Bragg peaks that belong to the main and impurity phases, especially when the amount of

the latter is significant.

Chapter

The results of the full pattern decomposition are shown in Table

6.3

as a

list of peak shape and lattice parameters, and also in Table

6.4

as a list of

Miller indices with the corresponding individual

l~~~~l~

and their standard

deviations. The array of intensity data can now be processed by any suitable

crystallographic software and used to calculate a Patterson function, or in a

combination with direct phase angle determination

algorithm(s) to solve the

crystal structure of LaNi4.s5Sno.15.

Table

6.3.

Parameters obtained at different stages during the full pattern decomposition of the

powder diffraction pattern of LaNi4,,5Sno.15.

Free parameters Refined values

Initial (default) parameters

Background (linear)

Background (linear),

U, V, W,

Background (linear),

U, V, W,

qo, a,

zero shift

Background (3rd order polynomial

plus hyperbolic term,

b.l),

U, V, W,

qo, a,

zero shift, asymmetry

Background (3rd order),

V, W,

qo,

ql, q2, a,

zero shift, asymmetry,

anisotropy plus broader peak bases

(12 FWHM's)

Same as above plus a second phase

included. Peak shape parameters of a

second phase were constrained to be

identical to those of the majority

phase due its small amount.

Background:

b4 and b.l, all zero

0.0100;

-0.0050;

0.0200;

0.2000; ql

0.0000;

0.0000

Asymmetry

0.020; Anisotropy (001)

0.0000

5.0421 A;

4.01 18 A; 620

0.000"

146.58; bl

-0.448

154.24; bl

-0.699

0.0164;

0.0599;

-0.0023; qo

0.2614

157.95; bl

-0.698

0.0403;

-0.0081;

0.0056; yo

0.4064;

5.0432 A;

4.0126 A; 620

0.02"

41.921; bl

-0.1 12; b2

4x10-~; b3

3x10-~;

b.1

3332.1;

0.031

0.0022;

0.0031; qo

0.4152;

Asymmetry

-0.025;

5.0419

4.01 15

620

0.049"

37.941; b,

-0.272; b2= 3x10"; b3

1x10.~;

b.1

3470.6;

0.0283;

-0.0046;

0.0058;

0.1066; q1

0.0086; q2

0.0000;

Asymmetry

-0.016; Anisotropy (001)

0.0165

5.0421 A;

4.01 16 A; 620

0.044"

31.562; bl

-0.423; b2

7x10-~; b3

7~10-~;

6.1

3654.2;

0.0281;

-0.0042;

0.0056;

0.1256; q1

0.0080; q2

0.0000;

Asymmetry

-0.016; Anisotropy (001)

0.0165

5.0419 A;

4.01 14 A; 620

0.044'

3.5416

(second phase, Nil.,Sn,)

Strictly speaking, in this case it is not necessary to solve the crystal

structure from first principles, because after finding that the Pearson's

symbol of the material is hP6, it is easy to identify the correct structure type

of this alloy by consulting Pearson's Handbook. Furthermore, in such a

small and high symmetry unit cell the possibilities to place different atoms

Crystal structure solution

525

are quite limited due to geometrical constraints, and chances are quite high

that this type of crystal structure is already known. Nonetheless, this

example is useful to illustrate how a simple combination of available data

about the chemical composition, unit cell contents and symmetry provides

required information, which may be used to locate all atoms in the unit cell.

Table

6.4.

The list of Bragg reflections with their corresponding observed structure factors

squared determined from Le Bail's full pattern decomposition of the powder diffraction

pattern of

LaNi, &no

Only the data for the major phase are listed.

hkl

Fobs 2

OIF~~~~~

010

1 0

2 1040

As established above, a total of 16 space groups are possible for

LaNi4,85Sno.15 but the highest symmetry is quite likely because the material is

an intermetallic compound. Hence, we will first concentrate our attention on

the space group

P61mmm. If the structure is solved in this space group

symmetry, then there is no need to test lower symmetry groups. However, if

the solution could not be found, the symmetry should be gradually lowered

until the crystal structure is solved, see

Figure

6.1.

We already know that we must locate a total of one La, and five Ni+Sn

atoms in the unit cell. According to the International Tables for

Crystallography,' only two sites in this space group symmetry have

International Tables for Crystallography, vol. A, Fifth revised edition, Theo Hahn, Ed.,

Published for the International Union of Crystallography by Kluwer Academic Publishers,

Boston/Dordrecht/London

(2002).

526 Chapter

multiplicity one and, therefore, are suitable to accommodate the La atom

(Table 6.5). These are: l(a) with coordinates of a point in 0,0,0, and l(b)

0,0,1/2. Considering the fact that La is the strongest scattering atom in this

crystal structure, it has the largest contribution to the phase angles of all

reflections. Hence, Ni atoms should be easily located from a Fourier map.'

Table

6.5.

Low multiplicity sites available in the space group

P6lmmm.

Site Coordinates of svrnmetricallv eauivalent points

As is easy to verify by calculating interatomic distances, the La atoms

can be accommodated in l(a) or l(b) sites, which differ only by a shift of the

origin of coordinates, and La-La distances are identical regardless of where

the La atom is placed. We place La in the

l(a) site. Calculation of phase

angles always involves calculation of

IF~~Y'~I

and therefore, it is also

possible to compute the corresponding figure of merit, RF,2 which is similar

to the Bragg residual (Eq. 6.20) except that the integrated intensities are

substituted with the absolute values of structure factors. After a La atom is

placed in the l(a) site, the

54.8%,

which is quite good considering that

five atoms are still missing from our model.

The coordinates and heights3 of the electron density peaks after

calculating a three-dimensional electron density distribution (Figure 6.12)

are listed in

Table

6.6. The strongest peak (No. 1) confirms the placement of

a La atom in the unit cell. It is easy to see that two additional and distinct

peaks (No. 2 and 3) appeared on the Fourier map. Their heights are about

112

of the expected number of electrons in pure Ni, which is normal given the

incomplete accuracy of reflection phases, which were calculated using only

the La atom. Between peaks No. 3 and

there is a sharp reduction in the

heights of the electron density maxima, and this feature usually indicates that

no more atoms are located in the unit cell.

The amount of Sn in the alloy is small and assuming random distribution of Ni and Sn in

the corresponding sites, the mixture is nearly pure nickel:

at.% Ni and

at.% Sn.

This figure of merit is customarily used in single crystal diffraction, where individual

IF~~P~~~~

are determined directly from the experiment.

Peak heights are usually used instead of integrated peak volumes for simplicity.

Crystal structure solution

527

Figure 6.12. The cross-sections of the three-dimensional Fourier map of LaNi4.ssSno.ls at Z

0 (left) and at Z= 112 (right) calculated using structure amplitudes listed in Table 6.4 and

phase angles determined by the La atom placed in the l(a) site. The triplets of numbers

indicate the coordinates of the strongest peaks in the unit cell. The following groups of peaks

are symmetrically equivalent to one another: 0,0,0; 1,0,0; 0,1,0 and 1,1,0 (all four correspond

to the La atom in

(a) and peak No. 1 in Table 6.6); 113,213,O and 213,113,O (peak No. 2 in

Table 6.4, and 1/2,0,1/2; 0,112,112; 112,112,112; 1,112,112 and 1/2,1,112 (peakNo. 3 in Table

6.6).

Table 6.6. The three-dimensional electron density distribution in the symmetrically

independent part of the unit cell of LaNi4,85Sno.ls calculated using the observed structure

factors determined from Le Bail's extraction (Table 6.4) and phase angles determined by the

La atom placed in the l(a) site of the space group P6lrnmm

(R;

54.8

%).

Fourier map peak number

Peak heighta

0 0

0.6667 0.3333 0

3 0.5 0 0.5

4 0.5 0 0 4

5 0 0 0.288 3

6 0.462 0.124 0.240 2

7 0.540 0.249 0.512 2

0.21 1 0.075 0.516 1

0.23 1 0.200 0.151 1

Peak heights have been normalized to represent approximate number of electrons in the

site occupied by La.

simple calculation of the interatomic distances between the La atom in

the l(a) site and all peaks listed in

Table

6.6

shows that only the distances

for peaks

and

are a good match for La-Ni distances. The distance

528

Chapter

between peaks 2 and

corresponds to the sum of radii of Ni atoms.

Furthermore, peak No.

represents coordinates of the 2(c) sites, and peak

No. 3 corresponds to the 3(g) sites in space group P6Immm. Thus, a total of

atoms have been placed in the unit cell of LaNi4.85Sno.15, i.e. exactly as

many as established from the gravimetric density of the alloy.

It is important to emphasize that La in the l(a) site has been confirmed by

the electron density calculation, although it is worth noting that in a heavy

atom approach it is often the case, that a single strongly scattering atom

always appears on the Fourier map even when it has been placed incorrectly.

However, if the location of the heavy atom is wrong, additional strong peaks

in the electron density distribution will normally be incorrect as can be easily

established by the computation of the interatomic distances. Such a model of

the crystal structure will be impossible to complete, i.e. the missing atoms

typically will not appear on the subsequent Fourier maps due to incorrectly

determined phase angles.

After all three independent atoms (peaks 1 through

in Table

6.6)

have

been included in computations assuming identical displacement parameters

in an isotropic approximation

0.5

8L2),

the resulting

6.9%

without

refinement. This value is excellent because

the powder diffraction pattern

is relatively simple with minimum overlap, and ii) the powder particles used

in the diffraction experiment were nearly ideal (spherical), thus preferred

orientation effects were also minimized. The following electron density

distribution (Figure

6.13

and Table

6.7)

was obtained using the newly

determined set of phase angles.

Figure

6.13.

The cross-sections of the three-dimensional Fourier map of LaNi4.ssSno.15 at

(left) and at

112

(right) calculated using structure amplitudes listed in

Table

6.4

and

phase angles determined

the La atom placed in the l(a) site and Ni atoms placed in the 2(c)

and 3(g) sites. The notations are identical to

Figure

6.12.

Crystal structure solution

529

Table

6.7. The three-dimensional electron density distribution in the symmetrically

independent part of the unit cell of LaNi,,,,Sn,,, calculated using the observed structure

factors determined from Le Bail's extraction

(Table

6.4) and phase angles determined by the

La atom placed in the l(a), and Ni atoms placed in the 2(c) and 3(g) sites of the space group

P6lrnmm (RF

6.9

%).

Fourier map peak number

Peak height

0.5

0.5 27

3 0.6667 0.3333 0

0 0 0.304 3

The major difference between the two Fourier maps shown in

Figure

6.12,

Figure

6.13,

Table

6.6, and

Table

6.7 is that peak heights of the

correctly placed atoms are much stronger than the heights of false peaks.'

Furthermore, the coordinates of false peaks vary but the coordinates of true

maxima remain the same. As is easy to verify by the calculation of distances,

none of the peaks listed below peak No.

Table

6.7 has a reasonable

distance to the La and Ni atoms already located in the unit cell.

Considering the low

RF,

the absence of new peaks on the second Fourier

map, which may correspond to additional atoms, and the fact that the

contents of the unit cell matches that established from the gravimetric

density of the material, we conclude that all atoms in the unit cell of

LaNi4.85Sno.15 have been located. It makes no sense to proceed with the least

squares refinement of atomic parameters using structure factors determined

from Le Bail's extraction, and the refinement of the crystal structure should

be completed using the Rietveld technique (see Chapter

7).

The coordinates

and possible distribution of atoms are listed in

Table

6.8 and the crystal

structure of the material is illustrated in

Figure

6.14.

Table

6.8. Coordinates of atoms in the unit cell of LaNi4,85Sno.15

determined from powder

diffraction data. All coordinates are fixed by symmetry of the corresponding sites and only

population and displacement parameters can and should be refined using Rietveld technique.

Atom Site

La ](a> 0 0 0

0.97Ni+0.03Sn 2(c) 113 213 0

0.97Ni+O.O3Sn 3(g) 112

False peaks (e.g. peak No.

Table

6.6, which is easily recognizable in

Figure

6.12)

appear on Fourier maps due to a variety of reasons: i) the largest contribution comes from

the truncation of the Fourier summation (Eq. 2.133) because only a limited amount of

diffraction data is available (see

Table

6.4); ii) the structure amplitudes are not exact,

especially when powder diffraction data were used in combination with Le Bail's

extraction, and iii) phase angles calculated using atomic parameters, which are not fully

refined, are still imprecise because we used randomly assigned displacement parameters

and assumed completely random distribution of Ni and Sn in two possible sites.

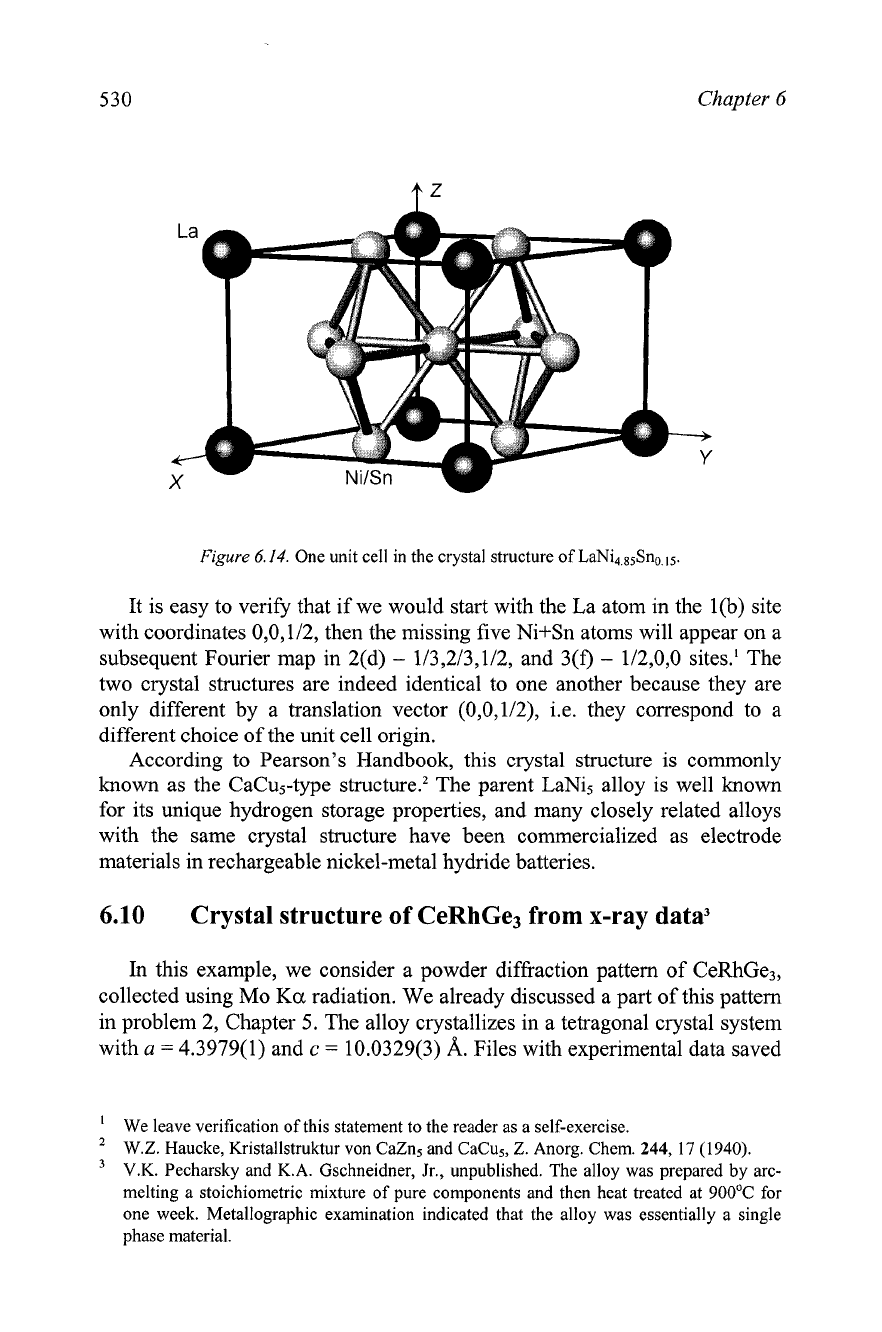
Chapter

Figure

6.14.

One unit cell in the crystal structure of LaNi,,8sSno,ls

It is easy to verify that if we would start with the La atom in the l(b) site

with coordinates 0,0,1/2, then the missing five Ni+Sn atoms will appear on a

subsequent Fourier map in 2(d)

1/3,2/3,1/2, and 3(f)

1/2,0,0 sites.' The

two crystal structures are indeed identical to one another because they are

only different by a translation vector (0,0,1/2), i.e. they correspond to a

different choice of the unit cell origin.

According to Pearson's Handbook, this crystal structure is commonly

known as the CaCu5-type struct~re.~ The parent LaNi5 alloy is well known

for its unique hydrogen storage properties, and many closely related alloys

with the same crystal structure have been commercialized as electrode

materials in rechargeable nickel-metal hydride batteries.

6.10

Crystal structure of CeRhGe3 from x-ray data3

this example, we consider a powder diffraction pattern of CeRhGe3,

collected using Mo

radiation. We already discussed a part of this pattern

in problem 2, Chapter

The alloy crystallizes in a tetragonal crystal system

with

4.3979(1) and

10.0329(3)

Files with experimental data saved

We leave verification of this statement to the reader as a self-exercise.

W.Z.

Haucke, Kristallstruktur von CaZn5 and CaCu5,

Anorg. Chem.

244,

(1940).

V.K.

Pecharsky and K.A. Gschneidner, Jr., unpublished. The alloy was prepared

arc-

melting a stoichiometric mixture of pure components and then heat treated at 900•‹C for

one week. Metallographic examination indicated that the alloy was essentially a single

phase material.

Crystal structure solution

53 1

in two different formats (Ch6Ex02-MoKa.dat and Ch6Ex02-MoKa.xy)

are found on the

accompanying this book.

Analysis of possible systematic absences indicates a body-centered lattice

with no additional forbidden reflections. Thus, one the following eight space

groups is to be expected: I4/mmm, I-, 142m, I4mm, 1422, I4/m, 1; or 14.

The measured gravimetric density of the alloy is 7.79 g/cm3. One unit cell

194.05 A3) contains two formula units of CeRhGe3

1.98

2) or a total

of two Ce, two Rh and six Ge atoms. Similar to the previous example, none

of the eight space groups can be excluded because all contain 2- and 4-fold

sites suitable to accommodate all three types of atoms in an ordered or

disordered fashion. Both

and Ge atoms have similar atomic volumes and

may occupy same sites simultaneously, while Ce atoms are much larger and

should occupy their own sites.

Full pattern decomposition has been performed using LHPM-Rietica.

Peak shapes have been represented using a pseudo-Voigt function. The

progression of the full pattern decomposition is shown by the corresponding

figures of merit, which are assembled in

Table

6.9, and the results are

illustrated in

Figure

6.15,

Figure

6.16, and

Table

6.10.

Table

6.9.

Figures of merit obtained during Le Bail decomposition of the powder diffraction

pattern of CeRhGe3. Wavelengths used: hKal

0.70932

hKa2

0.71361

Re,

2.96

Refined parameters Illustration R, RWD

Background (linear)

32.68 44.44 226.1

c 27.35 35.45 143.9

ro,

asymmetry

7.63 10.74 13.23

Background

(4th

order), broader base

4.89 7.03 5.67

All, with ~oward's' asymmetry

Figure

6.15

4.71 6.87 5.41

All, with

FCJ~

asymmetry

Figure

6.16

4.45 6.52 4.88

The use of Mo

radiation shifts all diffraction peaks to lower Bragg

angles and therefore, asymmetry effects are more severe than in the previous

example, where Cu

radiation was used. As a result, the order in which

parameters were refined was changed to avoid potential least squares

instability problems. When all parameters were refined in essentially the

same approximation as in the previous example (see row 5 in

Table

6.9), the

resultant figures of merit were satisfactory, but a careful analysis of

Figure

6.15 indicates that the selected peak shape function does not adequately

describe the observed peak shapes at low Bragg angles.

See the footnote on page

18.

Asymmetry was treated in the two-parameter approximation given by L.W. Finger,

D.E.

Cox, and A.P. Jephcoat, A correction for powder diffraction peak asymmetry due to axial

divergence, J. Appl. Cryst.

27,

892 (1994).