Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials

Подождите немного. Документ загружается.

412

Chapter

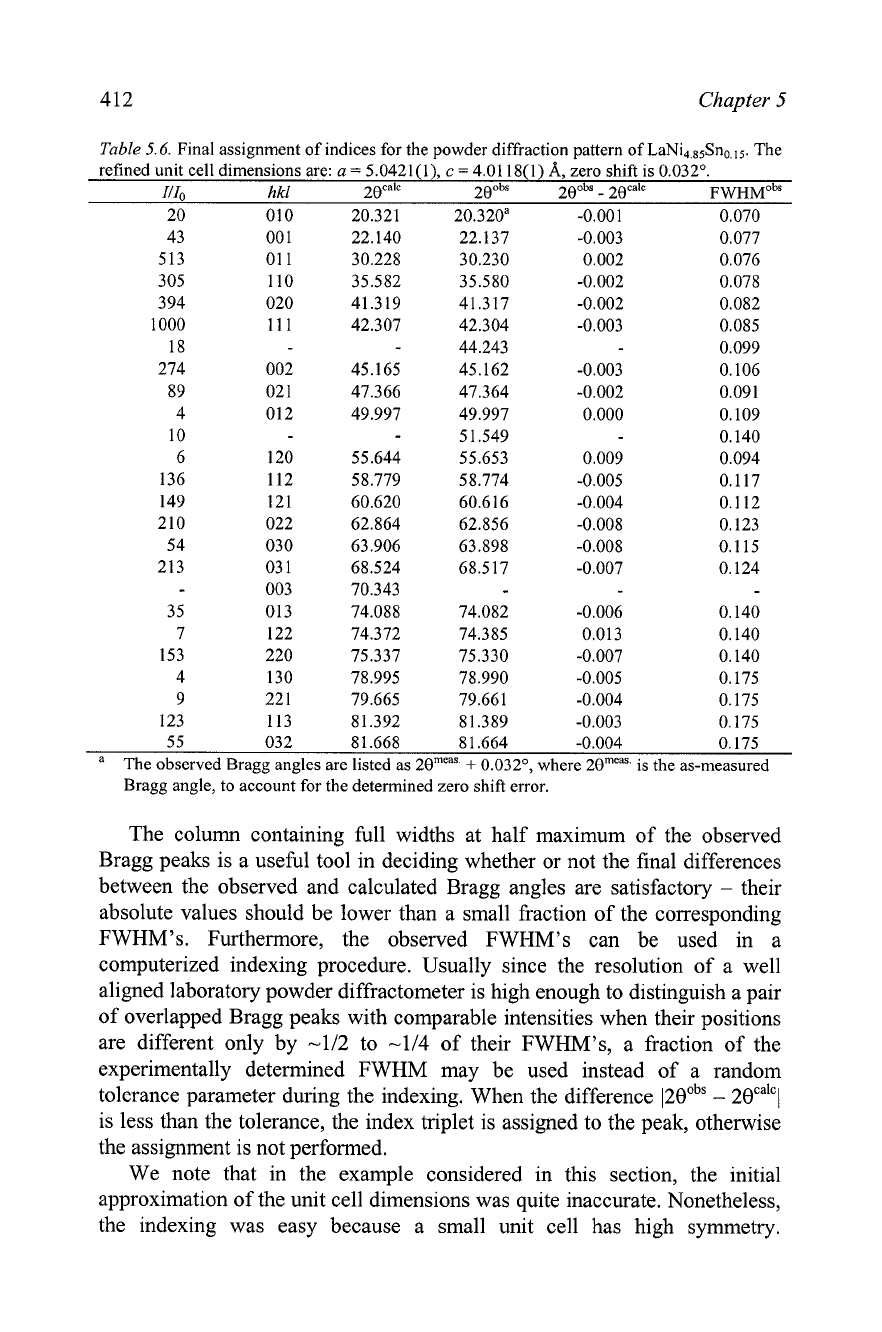
Table 5.6.

Final assignment of indices for the powder diffraction pattern of LaNi4.ssSno.lS. The

refined unit cell dimensions are:

5.0421(1),

4.01 18(1)

zero shift is

0.032O.

Ill, hkl

2e~a~~

2o0b" 200bs-2eca'~

FWHMO~~

20 010

20.321 20.320"

-0.00 1 0.070

43 00

22.140 22.137

-0.003 0.077

513 01 1

30.228 30.230

0.002 0.076

305 110 35.582

35.580

-0.002 0.078

394 020 41.319

41.317

-0.002 0.082

1000 111 42.307 42.304

-0.003 0.085

18 44.243 0.099

274 002 45.165 45.162 -0.003 0.106

89 02 1

47.366 47.364

-0.002 0.091

4 012 49.997 49.997 0.000 0.109

10 5 1.549 0.140

6 120 55.644 55.653 0.009 0.094

136 112 58.779 58.774 -0.005 0.117

149 121 60.620 60.616 -0.004 0.112

210 022 62.864 62.856 -0.008 0.123

54 030

63.906 63.898

-0.008 0.1 15

213 03

68.524 68.517

-0.007 0.124

003 70.343

3 5 013 74.088 74.082 -0.006 0.140

7 122 74.372 74.385 0.013 0.140

153 220 75.337 75.330

-0.007 0.140

4 130

78.995 78.990

-0.005 0.175

9 22

79.665 79.661

-0.004 0.175

123 113

8 1.392 81.389 -0.003 0.175

55 032 8 1.668 8 1.664 -0.004 0.175

The observed Bragg angles are listed as

2emeas

0.032',

where

2eme".

is the as-measured

Bragg angle, to account for the determined zero shift error.

The column containing full widths at half maximum of the observed

Bragg peaks is a useful tool in deciding whether or not the final differences

between the observed and calculated Bragg angles are satisfactory

their

absolute values should be lower than a small fraction of the corresponding

FWHM's. Furthermore, the observed FWHM's can be used in a

computerized indexing procedure. Usually since the resolution of a well

aligned laboratory powder diffractometer is high enough to distinguish a pair

of overlapped Bragg peaks with comparable intensities when their positions

are different only by -112 to -114 of their FWHM's, a fraction of the

experimentally determined FWHM may be used instead of a random

tolerance parameter during the indexing. When the difference

1290bS

29ca1C~

is less than the tolerance, the index triplet is assigned to the peak, otherwise

the assignment is not performed.

We note that in the example considered in this section, the initial

approximation of the unit cell dimensions was quite inaccurate. Nonetheless,

the indexing was easy because a small unit cell has high symmetry.

Unit cell determination and refinement

413

Consequently, only a small number of reflections were possible in the range

of measured Bragg angles and, for the most part, neighboring Bragg peaks

were clearly resolved in the diffraction pattern.

Rather inaccurate lattice parameters can result from a comparison with

known structures, serving as a basis for the initial guess. Considerable

differences between the real and guessed unit cell dimensions can make

indexing quite difficult, especially when large unit cells

and/or low

symmetry crystal structures are of concern. In many real cases, the best

possible accuracy in the initial unit cell dimensions is critical in order to

complete the indexing task in reasonable time, i.e. in a reasonable number of

iterations. The whole pattern can rarely be indexed using the initial and

imprecise approximation of lattice parameters due to inaccuracies in both the

unit cell dimensions and in the measured peak positions, especially when

systematic errors in the measured Bragg angles

(e.g. zero shift, sample

displacement

andlor transparency effects) are present.

5.4.2

Other crystal systems

Indexing of powder diffraction data in crystal systems other than

hexagonal when unit cell dimensions are known approximately, follows

essentially the same path as described in the previous section, except that the

proper form of Eq.

5.2

should be used in Eqs.

5.4

and

5.5.

In low symmetry

crystal systems, i.e. triclinic and monoclinic, two indices or one index,

respectively, should include negative values, i.e. they should vary from

-in,,,

to +i,,,, where i

for a complete generation of the list of possible

hkl.

Referring to the example of the two-dimensional reciprocal lattice

shown in

Figure

5.3, it is easy to see that for completeness, the list of

possible Bragg angles should include a set of reciprocal points with index h

varying from -h,,, to h,, and k varying from

to k,,,. In other words, this

describes the upper half of the circle drawn in this reciprocal lattice. We note

that all symmetrically independent combinations (hk) will also be generated

when h varies from

to h,,, but

varies from -kmx to k,,,, which

corresponds to a semi-circle on the right of

Figure

5.3.

The minimum and maximum values of Miller indices in three dimensions

are fully determined by the symmetrically independent fraction of the

reciprocal lattice as shown schematically in

Figure

5.6 for the six

distinguishable "powder" Laue classes. The same conditions are also listed

Table

5.7.'

Both

Table

5.7

and

Figure

5.6

account for the differences among "powder" Laue classes,

which are distinguishable at this stage, and are suitable for indexing of powder diffraction

patterns. For example, in Laue classes 6/m and 4/m ("powder" Laue classes 6/mmm and

4/mmm, respectively), the intensities of

hkl

and

khl

reflections are different, although the

Chapter

mmm

Figure

5.6.

Schematic representations of the fractions of the volume of the sphere

l/h) in

the reciprocal space in which the list of

hkl

triplets should be generated in six "powder" Laue

classes to ensure that all symmetrically independent points in the reciprocal lattice have been

included in the calculation of Bragg angles using a proper form of Eq. 5.2. The monoclinic

crystal system is shown in the alternative setting, i.e. with the unique two-fold axis parallel to

instead of the standard setting, where the two-fold axis is parallel to

b*.

Table

5.7.

Symmetrically independent combinations of indices in six "powder" Laue classes.

Independent

"Powder" Laue class Range of indices and limiting fraction of

conditionsa sphere volumeb

Triclinic, 1

-h.. .+h; -k.

..k;

0. ..+1

112

Monoclinic, 2/m

-h.. .+h; 0.

..k;

0..

.+1

1 14

Orthorhombic,

mmm

O...+h;

O...+k;

O...+l

118

Tetragonal, 4/mmm

O...+h; O...+k; O...+l; hlk

1/16

Hexagonal (=Trigonal), 6/mmrn

0.. .+h; 0..

.+k;

0..

.+1;

1/24

Cubic, m3m

O...+h; O...+k; O...+1; hsk; kll

1/48

Range and limiting conditions match the illustrations depicted in

Figure

5.6.

In general, any fraction of the sphere volume, symmetrically equivalent to that shaded in

Figure

5.6,

is acceptable.

corresponding Bragg angles remain identical. Consult the International Tables for

Crystallography, vol.

for proper intensity relationships in other Laue classes.

Unit cell determination and refinement

415

Instead of using a spreadsheet for generating the list of possible

hkl's and

calculating Bragg angles using known or approximately known unit cell

dimensions, it is possible to use one of several computer programs that can

be downloaded from the International Union of Crystallography' or from the

Collaborative Computational Project No.

142 Web sites. Nearly all of them

are simple to use and they require minimum data input. The latter typically

includes symmetry in the form of space group symbol or crystal system

name, unit cell dimensions, wavelength and maximum Bragg angle to limit

the amount of output data. Furthermore, nearly every commercially available

crystallographic software product includes a procedure for generating a

complete list of possible hkl's along with the corresponding interplanar

distances and Bragg angles calculated from the known unit cell dimensions.

5.5

Reliability

indexing

Regardless of which tools were used in the indexing of the powder

diffraction pattern, the most reliable solution should result in the minimum

discrepancies in the series of simultaneous equations (Eq. 5.5 or its

equivalent for a different crystal system) constructed with the observed

substituted into the left hand side and the assigned index triplets and refined

unit cell dimensions substituted into the right hand side of each equation.

While the minimum combined discrepancy is easily established

algebraically,

e.g. as the sum of the squared differences

usually it is not enough to achieve the minimum

and assume that the

correct unit cell has been found. In Eq.

5.6,

represents the number of the

observed Bragg peaks. Obviously,

when the unit cell dimensions are

increased (e.g. see Eq. 5.5) or its symmetry is lowered (see Table

5.7),

this

results in an increased number of possible combinations of indices in the

same range of Bragg angles. Ultimately, infinitesimal

can be reached when

the total number of possible combinations of hkl triplets approaches infinity

but

remains constant.

Because of this ambiguity, several other criteria shall be considered

before an indexing result is accepted, i.e. a final unit cell selection is made,

especially during the ab initio indexing. The somewhat related to one

another norms are as follows (all other things are assumed equal):

416 Chapter

a) The preference generally is given to the unit cell with the highest

symmetry because high symmetry translates into a low number of

symmetrically independent reciprocal lattice points (see Figure

5.6)

and,

therefore, the lowest number of possible Bragg reflections. For example,

when the following three unit cells (Table 5.8) result in the successful

indexing, the best of the three is represented by a tetragonal symmetry.

Table

5.8.

Example of three unit cells with nearly identical volumes but different symmetry.

Crystal system

(A)

("1

Bravais lattice

Monoclinic

7.128 9.253 7.127 89.98

Orthorhombic

9.253 7.127 7.129 90

Tetragonal (best)

7.127 7.127 9.255 90

The unit cell with the smallest volume usually represents the best

solution because it leaves the smallest number of possible index triplets

unassigned to at least one of the observed Bragg peaks.

the example

shown in Table 5.9, the third row is likely the best solution.

Table

5.9.

Example of three unit cells with identical symmetry but different volumes.

Crystal system

(A)

(A3) Bravais lattice

Orthorhombic

7.128 9.253 5.613 370.21

Orthorhombic

9.253

7.128

1 1.226 740.42

Orthorhombic (best)

4.627

5.613

7.128 185.12

c) The preference shall be given to a solution, which results in the smallest

number of possible hkl triplets in the examined range of Bragg angles.

other words, if among several solutions, which are otherwise equivalent,

one has a centered lattice and all the others are primitive, the centered

lattice is typically the best (see Table 5.10).

Table

5.10.

Example of two unit cells with identical symmetry and volumes but different

Bravais lattices.

Crystal system

(A)

(A3) Bravais lattice

Tetragonal (best)

7.127

7.127 9.255

470.28

Tetragonal

7.127

7.127 9.255

470.28

d) Finally, the resulting

(Eq.

5.6)

or a similar algebraic measure should be

at its minimum for the most preferred indexing solution.

We note that the benchmarks listed above must be applied altogether. For

example, it is nearly always possible to choose the highest symmetry crystal

system

(i.e, cubic) and a large unit cell to dubiously assign index triplets to

all observed Bragg peaks and obtain acceptable

This happens because the

density of points in the reciprocal lattice is proportional to the volume of the

Unit cell determination and refinement

417

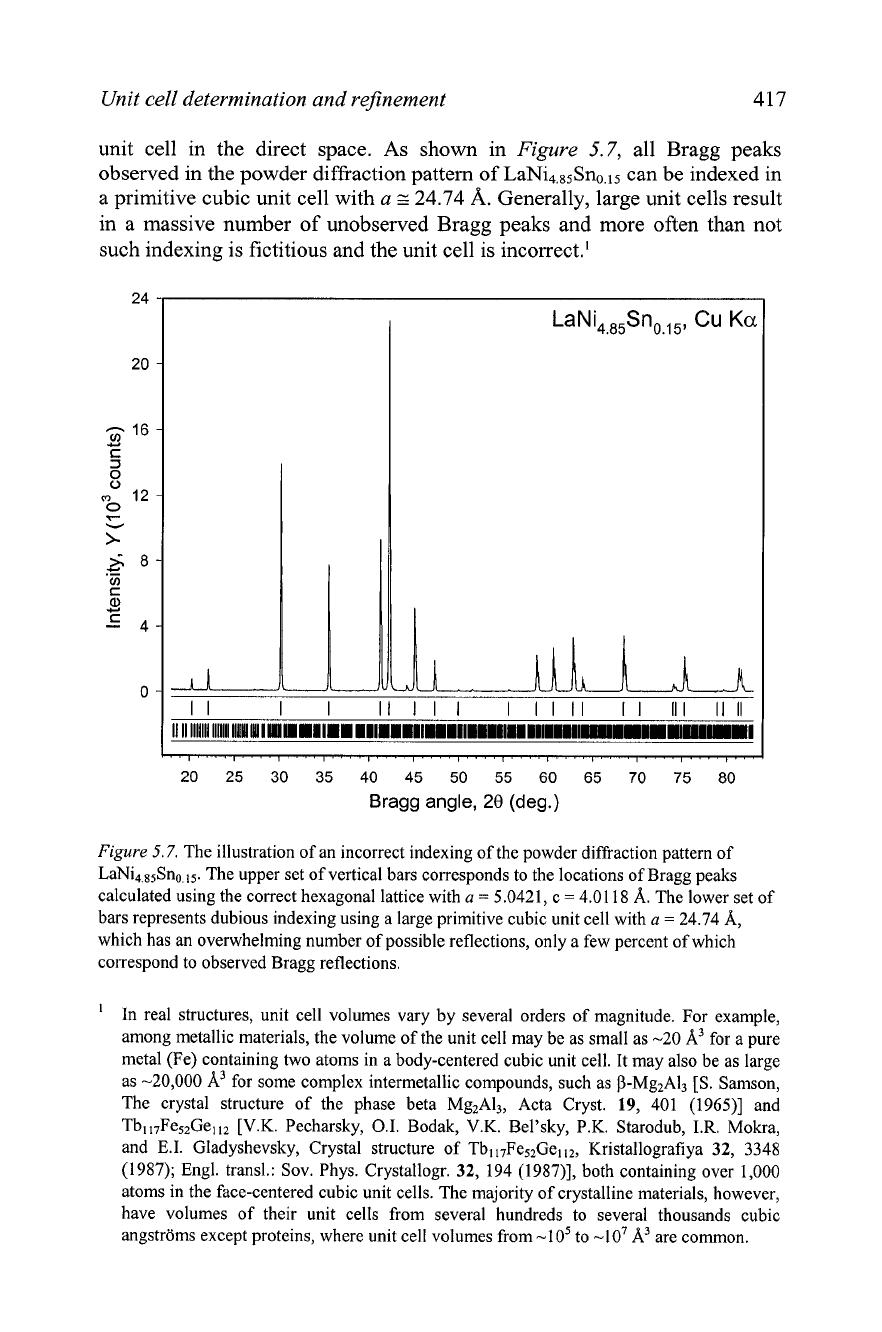
unit cell in the direct space. As shown in

Figure

5.7, all Bragg peaks

observed in the powder diffraction pattern of LaNi4.85Sn0.15 can be indexed in

a primitive cubic unit cell with

24.74

Generally, large unit cells result

in a massive number of unobserved Bragg peaks and more often than not

such indexing is fictitious and the unit cell is incorrect.'

20 25 30 35

45 50 55 60 65 70 75 80

Bragg angle,

(deg.)

Figure

5.7.

The illustration of an incorrect indexing of the powder diffraction pattern of

LaNi4,85Sno.,5. The upper set of vertical bars corresponds to the locations of Bragg peaks

calculated using the correct hexagonal lattice with

5.0421, c

4.01 18 A. The lower set of

bars represents dubious indexing using a large primitive cubic unit cell with

24.74 A,

which has an overwhelming number of possible reflections, only a few percent of which

correspond to observed Bragg reflections.

In real structures, unit cell volumes vary by several orders of magnitude. For example,

among metallic materials, the volume of the unit cell may be as small as -20 A3 for a pure

metal (Fe) containing two atoms in a body-centered cubic unit cell. It may also be as large

as -20,000

for some complex intermetallic compounds, such as P-Mg2AI3 [S. Samson,

The crystal structure of the phase beta Mg2AI3, Acta Cryst.

19,

401 (1965)l and

Tbl17Fe52Gell,

[V.K.

Pecharsky, 0.1. Bodak, V.K. Bel'sky, P.K. Starodub,

I.R.

Mokra,

and E.I. Gladyshevsky, Crystal structure of Tbl17Fe52Gel12, Kristallografiya

32,

3348

(1987); Engl. transl.: Sov. Phys. Crystallogr.

32,

194

(1987)], both containing over 1,000

atoms in the face-centered cubic unit cells. The majority of crystalline materials, however,

have volumes of their unit cells from several hundreds to several thousands cubic

angstroms except proteins, where unit cell volumes from

-lo5 to -lo7 A3 are common.

418 Chapter

It is worth noting, however, that when the true crystal structure is derived

from

minor distortion of a small unit cell,

e.g. when the so-called

superstructure has been formed or when the real structure is perturbed by a

long period, small amplitude modulation function, many Bragg peaks and

often the majority of them, may have extremely low intensity and become

unobserved. These cases require special attention during the indexing, and

detailed consideration of related subjects exceeds the scope of this book.

The quality and the reliability of indexing, therefore, is routinely

characterized by means of various numerical figures of merit

(FOM's), and

their significance becomes especially high when indexing is performed using

a computer program. Numerous FOM's have been introduced and used with

variable success in the powder diffraction data indexing process. We will

consider two of the most frequently used figures of merit. Both have been

adopted by the International Centre for Diffraction Data to characterize the

quality of indexing of patterns included into the Powder Diffraction File.

5.5.1

The

figure of merit

The so-called

figure of merit has been introduced by Smith and

Snyder.' It is defined as

where

is the number of the observed Bragg peaks.

NpoSs

is the number of independent Bragg reflections possible up to the

observed diffraction peak, and

AT0

z1~20~

z120;bs

20~''

is the average absolute

i=1

difference between the observed and calculated 2ehk[.

In other words,

N,,,,,

is the number of symmetrically independent points

in the reciprocal lattice limited by a sphere with the diameter d*N

lldN) as

established by Eq. 5.3 after substituting the Bragg angle, ON, of the

Nth

observed Bragg peak for €Ihkl. Additional restrictions are imposed on

N,,,

high symmetry crystal systems: when reciprocal lattice points are not related

by symmetry but when they have identical reciprocal vector lengths due to

specific unit cell shape

(e.g. h05 and h34 in the cubic, or 051 and 341 in the

G.S. Smith and

R.L.

Snyder,

FN:

a criterion for rating powder diffraction patterns and

evaluating the reliability of powder pattern indexing,

Appl. Cryst.

12,60

(1979).

Unit cell determination and refinement

419

tetragonal crystal systems), then only one is included into calculating

N,,,.

On the contrary, when the identity of the reciprocal lattice vectors lengths is

coincidental [eg as shown for d(32)

(42)

in Figure 5.31, both are included

into the calculated N,,,. The

figure of merit is usually reported in the

form

For example, in the indexed powder diffraction pattern of LaNi4,85Sno,lS

shown in Table 5.6 after the unit cell dimensions have been refined, the

resulting FN, excluding the two impurity peaks, is

F22

208.4(0.005, 23).

The same figure of merit, calculated using the indexing results and unrefined

unit cell dimensions (Table 5.5), is

F22

26.1(0.037, 23). The best FOM,

F22

208.4(0.005, 23), is interpreted as follows: the figure of merit for the

22 observed Bragg peaks is 208.4, the average absolute 20 difference is

0.005", and the total number of possible symmetrically inequivalent Bragg

peaks is 23. The best indexing result usually has the highest FN. Although it

is difficult to establish strict guidelines on the values of

corresponding to

a reasonable indexing, the

usually should be greater than 10; the lowest

average 29 difference should be lower than 0.02", and the number of

possible Bragg peaks, Nposs, should be the same or slightly larger than the

number of the observed peaks, N.

5.5.2

The

MzO

figure

merit

The second fi-equently used figure of merit, M20, has been introduced by

de WolfF and it is defined as

where:

N,,,, has the same meaning as in the FN, except it is computed for

Om,

020, i.e. it is the number of symmetrically independent points in the

reciprocal lattice up to the 2oth observed Bragg peak.

d *2

l/d represents the square of the length of the reciprocal

vector.

P.M.

Wolff, A simplified criterion for

the

reliability of a powder pattern indexing,

Appl. Cryst.

108

(1968).

420 Chapter

Q20

is the corresponding Q-value for the 2oth observed Bragg peak, and

~AQ~

Q;::

is the average absolute

i=,

difference between the observed and calculated

Qhkl

for the first 20 Bragg

peaks.

The

M20

FOM is nearly always calculated for the first 20 observed

reflections, unless the total number of the observed Bragg peaks is less than

20. Sometimes, when

20, the value of

can be reported instead of

M20.

these cases,

Eq.

5.9, is converted into

Once again referring to the two examples of indexing (Table

5.5

and

Table

5.6)

the respective

Mzo

values are 39.1 and 278.1. Similar to FN, the

more reliable indexing yields the higher

Mzo.

However, it is even harder to

specify an "acceptable" range of the

Mzo

values: when compared to FN, the

M20

FOM is strongly dependent on both the complexity of the pattern and

unit cell volume. Therefore, one should look for a solution with the

M20

figure of merit, which is distinctly larger than the others. If all solutions have

about the same and low

M20

FOM's, e.g. all are between

and

it is highly

likely that none of them is a correct solution of the indexing problem.

5.6

Introduction to

initio

indexing

The complexity of indexing powder diffraction data without prior

knowledge of either or both the symmetry and dimensions of the unit cell

(i.e. assignment of indices from first principles, based strictly on the

relationships between the measured lengths of the reciprocal lattice vectors)

is inversely proportional to the symmetry of the lattice

the higher the

symmetry, the simpler the indexing process. Although today the actual

indexing is hardly ever performed without employing one or several freely

available or commercial computer programs,' we believe that it is important

to consider essential mathematical background, which for many years was

employed successfully to find solutions of indexing problems "manually".

The most comprehensive collections of various crystallographic software products are

found at the International Union of Crystallography Web site at http://www.iucr.org and at

the Collaborative Computational Project No.

for Single Crystal and Powder Diffraction

Web site at http://www.ccpl4.ac.uk.

Unit cell determination and refinement

42 1

We will begin with the cubic crystal system, where the assignment of

indices is nearly transparent and then consider the theory behind the

ab initio

indexing in crystal systems with tetragonal and hexagonal symmetry.'

Indeed, as with any kind of experimental work, experience is paramount, and

we hope that the contents of this section may help the reader to achieve

accurate solutions of real life indexing tasks successfully.

Accurate indexing from first principles rests on the four cornerstones:

1. The availability of Bragg peaks observed at the lowest possible Bragg

angles. These peaks are critically important because they have the

simplest indices (usually -2

2, -2

2 and -2

2), which

considerably limits the possibilities of locating the corresponding vectors

in the reciprocal lattice and therefore, simplifies the whole process of

restoring reciprocal lattice vector directions from their lengths.

2. The absence of a large number of extinct Bragg peaks, especially at low

Bragg angles. For example, if due to a variety of reasons all observed

Bragg peaks taken into account during the indexing have one of the

indices divisible by two, then the resulting unit cell dimension will be

112

of the true value.

The high absolute accuracy including the absence of any kind of a

systematic error affecting the measured Bragg angles. This requirement is

obvious as only the lengths, but not the directions of the reciprocal

vectors are measurable in powder diffraction. The presence of even a

small systematic error

(e.g. sample displacement andor zero shift errors)

may considerably affect the outcome of the indexing because it usually

has the strongest influence on the lowest Bragg angle peaks, which are

critical for successful indexing (see item 1 in this list, and

Eq.

5.29 and

Figure

5.18,

below).

any case, systematic experimental errors should

be minimized by proper alignment of the instrument. If necessary, an

additional set of experimental data can be collected with a

well-

characterized internal standard added to the studied powder thus enabling

one to eliminate the present systematic errors from the data before

attempting

ab initio

assignment of indices.

The absence of impurity Bragg peaks in the array of experimental data. If

this requirement is not met and one or more impurity peaks are included

in the indexing attempt, it is nearly always true that the reciprocal vectors

from the impurity phase do not fit within the correct reciprocal lattice of

the major crystalline phase. The resulting unit cell, if a solution is ever

found, more often than not will be incorrect as it describes both the

vectors from the major phase and the impurity

phase(s) in the same

An excellent description of the

initio

indexing in all crystal systems can be found in

Lipson and

Steeple, Interpretation of x-ray powder diffraction patterns, Macmillan,

London; St. Martin's Press, New York

(1970).