Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials

Подождите немного. Документ загружается.

422 Chapter

reciprocal lattice. Certain

initio indexing procedures, e.g. those that

are incorporated into

TREOR

and

IT0

(see sections

5.1

1.1

and

5.1

1.3

below), automatically skip some Bragg peaks that do not fit in a trial

lattice. This feature may help in indexing patterns containing some

impurities but on the other hand, it may also result in the incorrect,

usually overly simplified solution when Bragg peaks from a major phase

are accidentally excluded.

5.7

Cubic crystal system

Cubic symmetry of a material is always a good guess when a powder

diffraction pattern contains just a few peaks, or when there are sequences of

observed Bragg peaks that appear nearly equally spaced, especially at low

Bragg angles. Clearly, some experience in working with powder diffraction

data is needed to make this judgment from a visual analysis of

Y(8).

However, the ab initio indexing algorithm is so simple in the case of cubic

symmetry, that nearly always it is justifiable to attempt cubic indexing and

either confirm or dismiss this option.

When the crystal system is cubic, the general form of equation 5.2 is

simplified to

or in terms of the reciprocal lattice parameter

Since h,

and

are integers, the sums of their squares, (h2

p),

are

also integer numbers. Thus, equation 5.12 can be written as follows

Qhkl

Ajk,a (5.13)

where Qjkl

d*2hkl

l/d2jkl and

Ahkl

(h2

P).

The former is

established from the experiment for each Bragg peak using Eq. 5.3 and the

latter is a positive integer, which depends on the values of h,

and

in the

index triplet. Certain whole numbers, e.g.

15 and others, given by

Unit cell determination and refinement

423

where i and

are positive integers, cannot be represented as a sum of squares

of any three integers and therefore, are forbidden in Eq. 5.13.

Assume that we have a set of experimental data where the observed

Bragg angles have been converted into an array of Q-values. Then, if the

crystal lattice is cubic, the following system of simultaneous equations can

be written to associate each Bragg peak with a certain combination of hkl

triplets:

As follows from the second form of Eq. 5.15, the observed array of

Q-

values should have a common divisor, which results in the array of integers

or nearly integers, considering the finite accuracy of the measured Bragg

angles. This common divisor is nothing else than the inverse of the square of

the edge of the cubic unit cell in the direct space since a*

lla.

The algorithm of indexing to test for cubic symmetry is shown in the

form of a flowchart in Figure

5.8.

After the array of Bragg angles have been

converted to Q-values, the next step is to normalize it and find the integers

A', A2,

AN. The simplest way to do so is to divide all Q-values by the

smallest number present in the array, i.e. Qjlklll

Q'. If the resulting array of

A', A',

. .

contains whole numbers (to within a few hundredth's), the

lattice parameter is calculated and the corresponding values of the hikili

triplets are determined based on the values of

after verification that no

forbidden integers (e.g.

15, etc., see Eq. 5.14) are present in the array A.

When the first normalization step results in clearly non-integer values in

the array A, indexing still may be completed when the obtained A', A',

AN are multiplied by 2, 3, 4, etc. If the crystal system is truly cubic, a simple

visual analysis of the array

after the first normalization usually enables one

to determine the needed integer multiplier easily. For example, when

decimal fractions of all A-values are close to 0 and 0.5, multiplying every

number in the array

by 2 will result in all integers. Similarly, when the

fractions are -0, -0.33 and -0.66, the multiplier is 3, and so on. When the

algorithm shown in Figure

5.8

is realized as a computer program then visual

analysis of data in

is usually impractical and the value of n is determined

automatically, based on somewhat arbitrary tolerances that establish which

value is taken as a whole number and which is not.

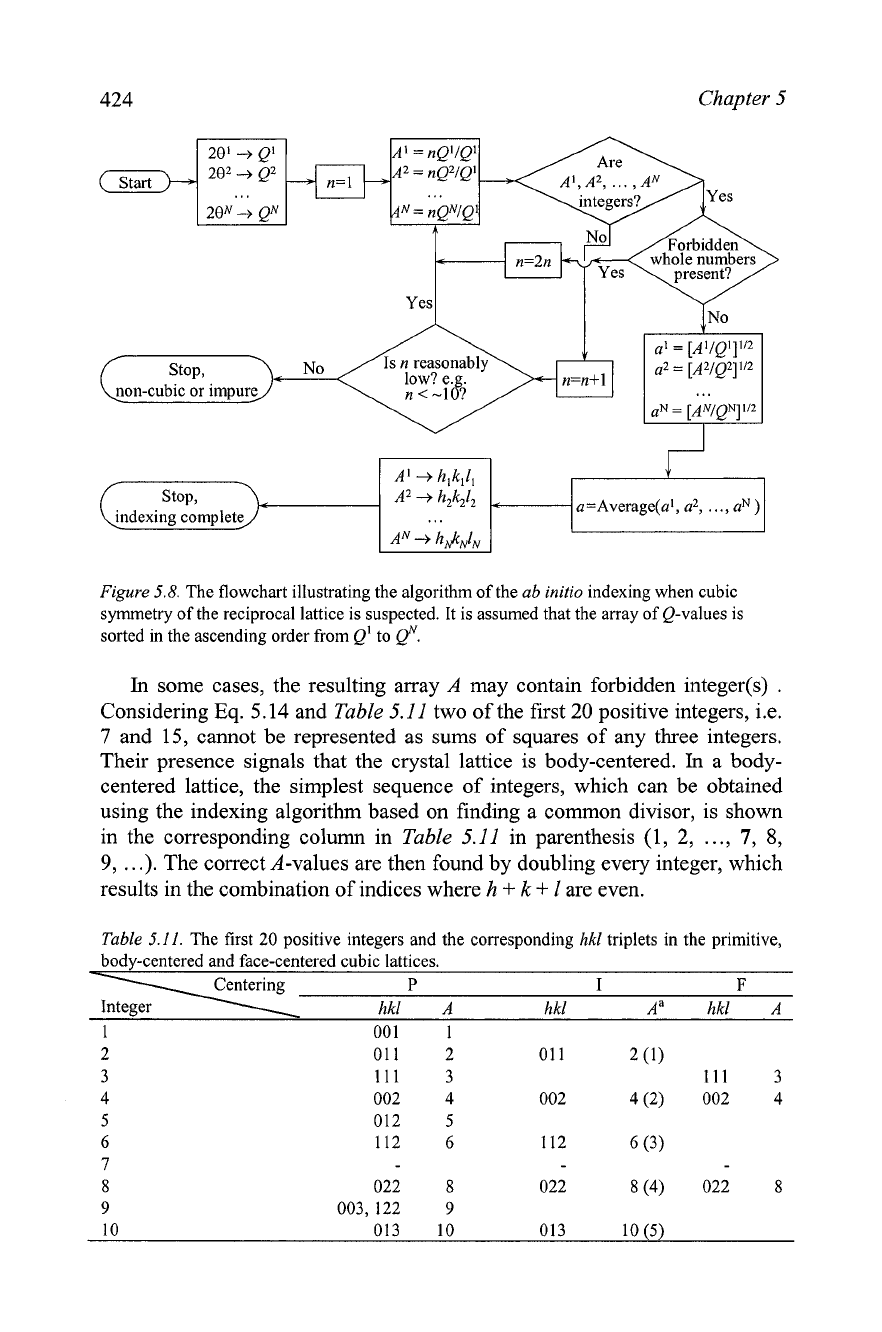
424

Chapter

Yes

Flgure

5.8.

The flowchart illustrating the algorithm of the

initio

indexing when cubic

symmetry of the reciprocal lattice is suspected. It is assumed that the array of Q-values is

sorted in the ascending order from

some cases, the resulting array

may contain forbidden integer(s)

Considering

Eq.

5.14 and

Table

5.11

two of the first

positive integers, i.e.

and 15, cannot be represented as sums of squares of any three integers.

Their presence signals that the crystal lattice is body-centered. In a body-

centered lattice, the simplest sequence of integers, which can be obtained

using the indexing algorithm based on finding a common divisor, is shown

in the corresponding column in

Table

5.11

in parenthesis

(1,

...,

.).

The correct A-values are then found by doubling every integer, which

results in the combination of indices where

are even.

Table

5.11.

The first 20 positive integers and the corresponding

hkl

triplets in the primitive,

body-centered and face-centered cubic lattices.

hkl

001

Unit cell determination and rejkement

425

hkl

11 113 11 113 11

20 024 20 024 20 (10) 024 20

The numbers in parenthesis indicate the simplest sequence of integers, which describes

the relationships between the sums of

h2,

and

in the body-centered cubic lattice. The

presence of forbidden integers (e.g.

which is highlighted in bold) enables one to

differentiate between the primitive and body-centered cubic lattices during the

initio

indexing.

5.7.1

Primitive cubic unit cell:

LaBs

We now consider the application of the indexing algorithm described

above using experimental powder diffraction data collected from two

different cubic materials. The first one is the standard reference material

La&, which was available from the National Institute of Standards and

Technology (NIST) under the catalogue number SRM-660.' The

experimental powder diffraction pattern is shown in

Figure

5.9

and the

certified lattice parameter of the material is

4.15695(6)

The observed

Bragg peak positions were determined using a profile fitting procedure and

the least squares standard deviations in the observed Bragg angles did not

exceed 0.001" of 20. These are listed in

Table

5.12

and can be found in

Excel spreadsheet data file

Ch5Ex02~PrimitiveCubic.xls

on the

CD.

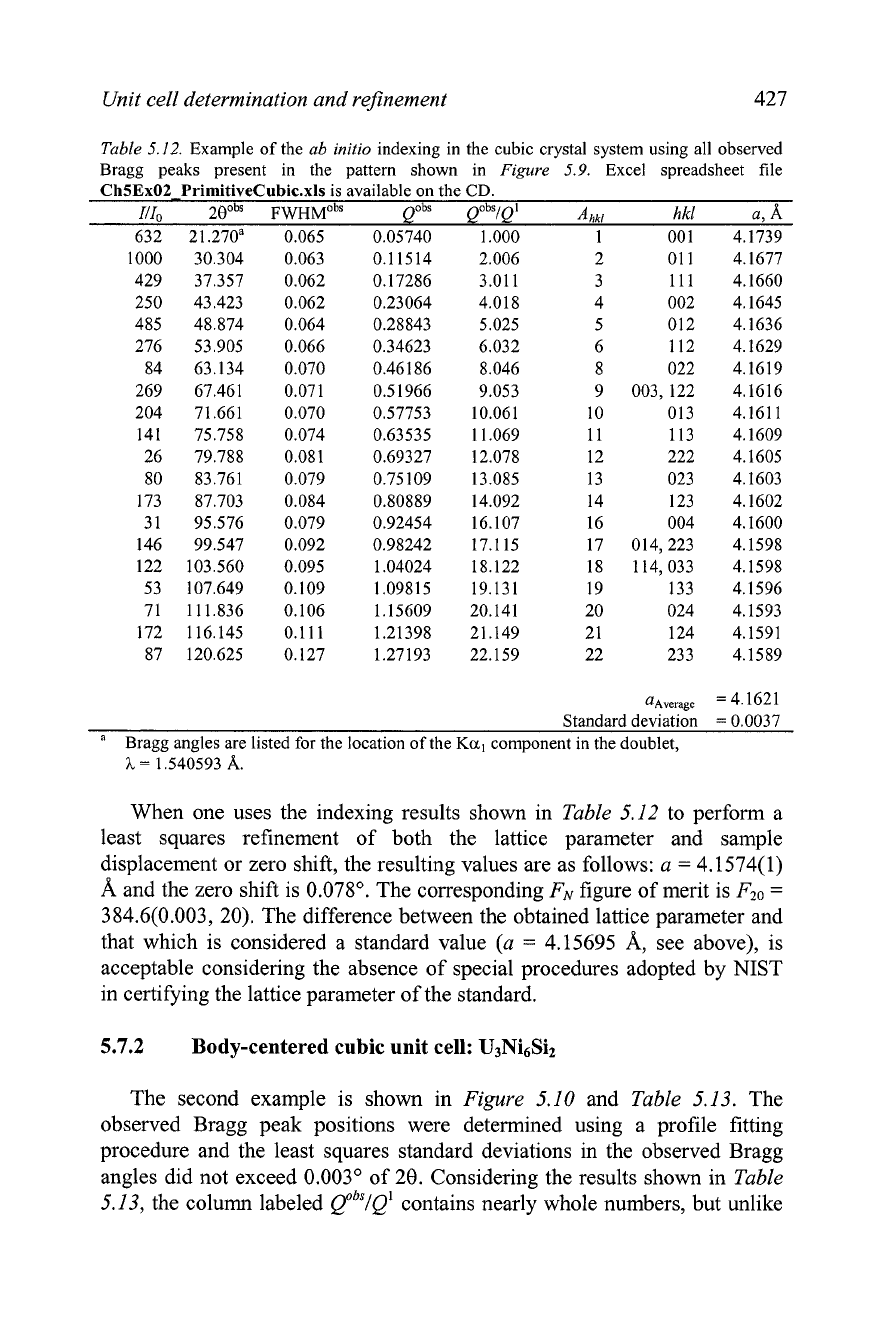
Table

5.12

shows how the indexing has been performed. First, QobS are

calculated for each 20ObS:

Second, the values from this column are normalized by dividing them by

the smallest observed Q, i.e. by 0.05740. This yields the column of data

marked as QobS/Q'.

SRM-660 has been replaced by SRM-660a and the latter is available from NIST. Consult

http:Nsrmcatalog.nist.gov/

for details.

426

Chapter

LaB,

(NIST SRM-660),

20 30 40 50 60 70 80 90 100 110 120

Bragg

angle,

(deg.)

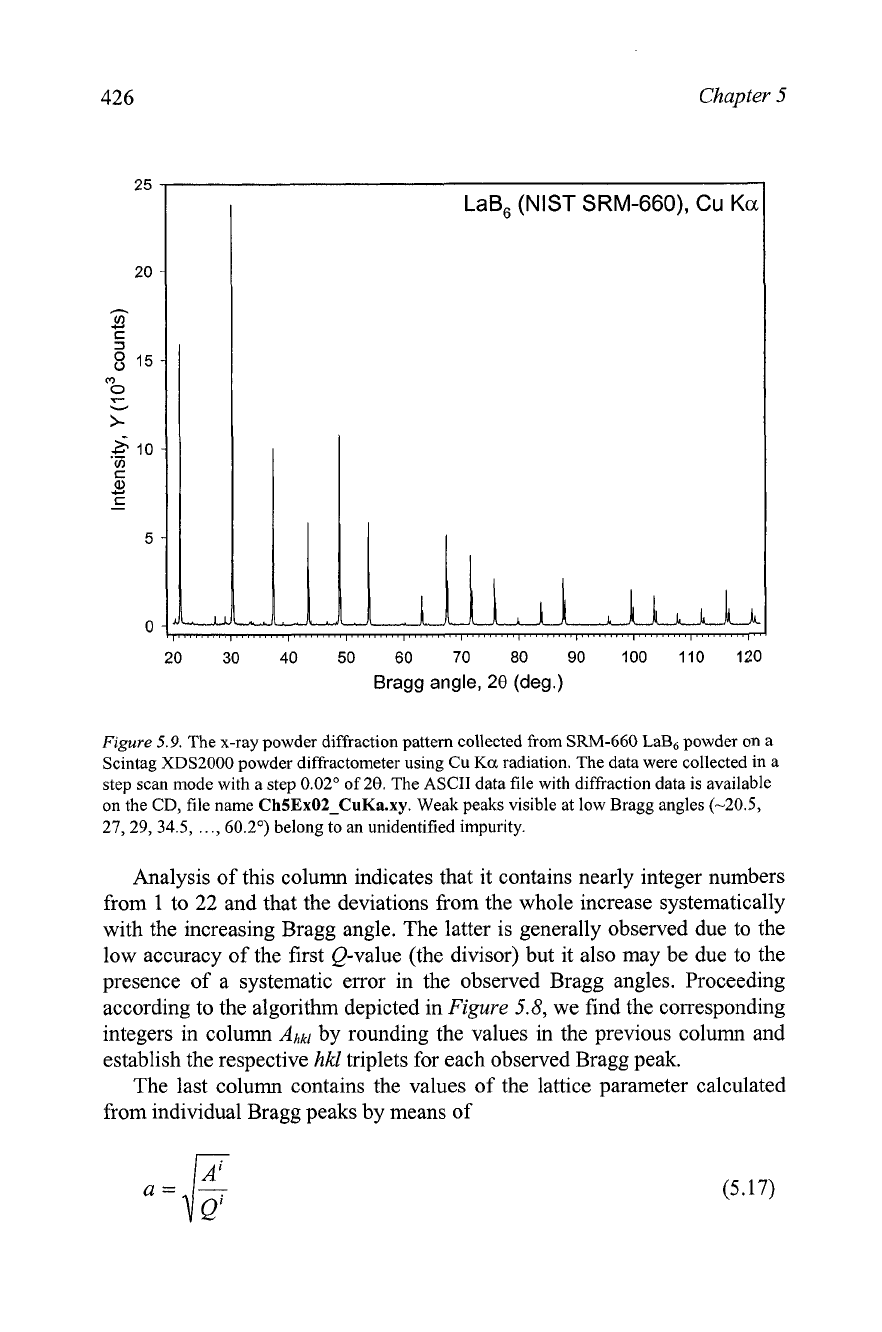
Figure

5.9.

The x-ray powder diffraction pattern collected from SRM-660 LaB, powder on a

Scintag XDS2000 powder diffractometer using

radiation. The data were collected in a

step scan mode with a step 0.02' of

20.

The ASCII data file with diffraction data is available

on the CD, file name

ChSExOZ-CuKa.xy.

Weak peaks visible at low Bragg angles (-20.5,

27,29,

34.5,

., 60.2") belong to an unidentified impurity.

Analysis of this column indicates that it contains nearly integer numbers

from 1 to

and that the deviations from the whole increase systematically

with the increasing Bragg angle. The latter is generally observed due to the

low accuracy of the first Q-value (the divisor) but it also may be due to the

presence of a systematic error in the observed Bragg angles. Proceeding

according to the algorithm depicted in

Figure

5.8,

we find the corresponding

integers in column

Ahkl

by rounding the values in the previous column and

establish the respective

hkl

triplets for each observed Bragg peak.

The last column contains the values of the lattice parameter calculated

from individual Bragg peaks by means of

Unit cell determination and rejnement

427

Table

5.12.

Example of the

initio

indexing in the cubic crystal system using all observed

Bragg peaks present in the pattern shown in

Figure

5.9.

Excel spreadsheet file

ChSEx02

PrimitiveCubic.xls

is available on the

CD.

14,

2BobS

FWHM'~~

obs

Q"~"Q'

Ahkl

hkl

632 21.270a 0.065 0.05740

.OOO 1 001 4.1739

Standard deviation

0.0037

Bragg angles are listed for the location of the

KCL,

component in the doublet,

S40593

When one uses the indexing results shown in

Table

5.12 to perform a

least squares refinement of both the lattice parameter and sample

displacement or zero shift, the resulting values are as follows:

4.1574(1)

and the zero shift is 0.078". The corresponding

figure of merit is

FZ0

384.6(0.003, 20). The difference between the obtained lattice parameter and

that which is considered a standard value

4.15695 A, see above), is

acceptable considering the absence of special procedures adopted by

NIST

in certifying the lattice parameter of the standard.

5.7.2

Body-centered cubic unit cell:

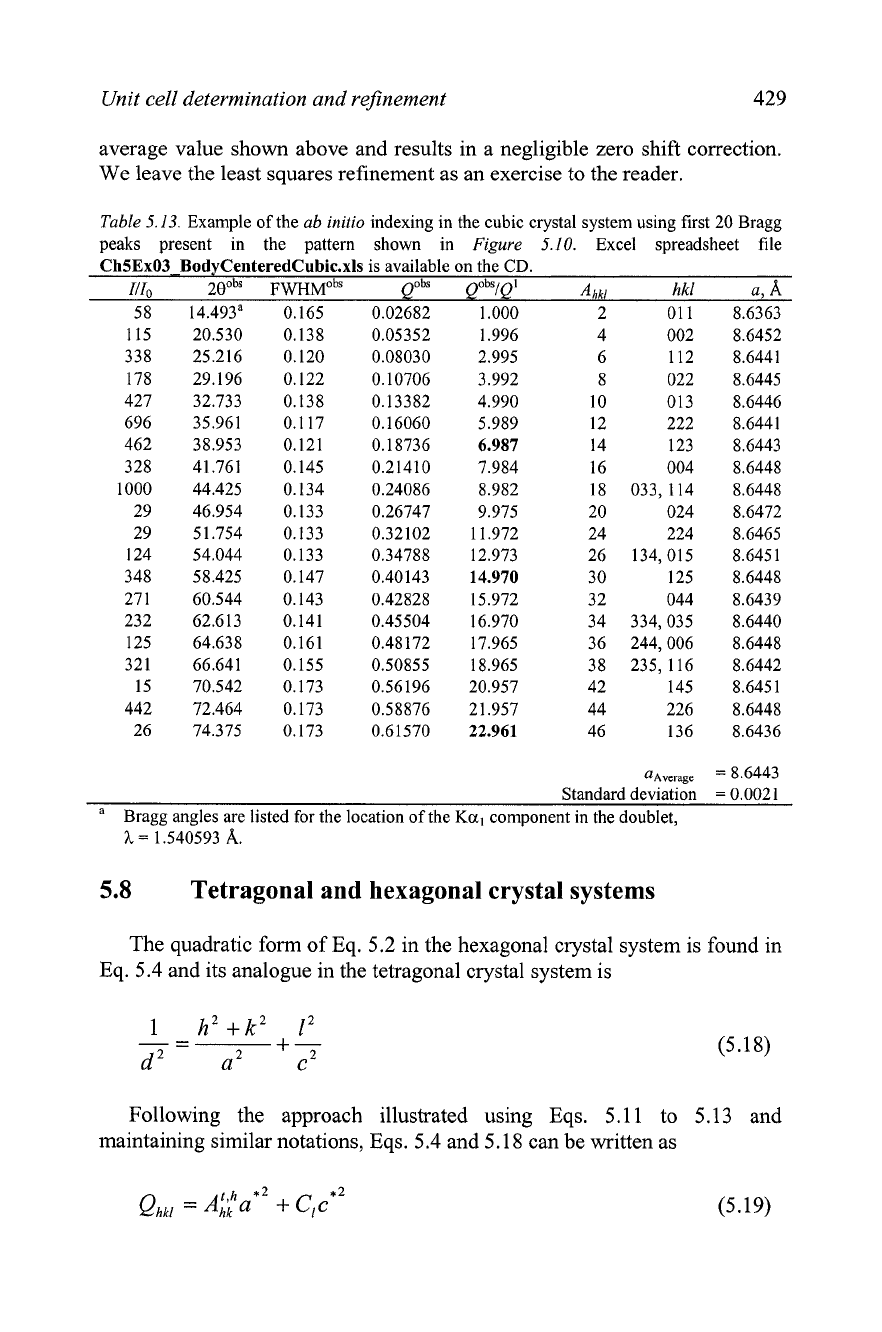
U3Ni6Si2

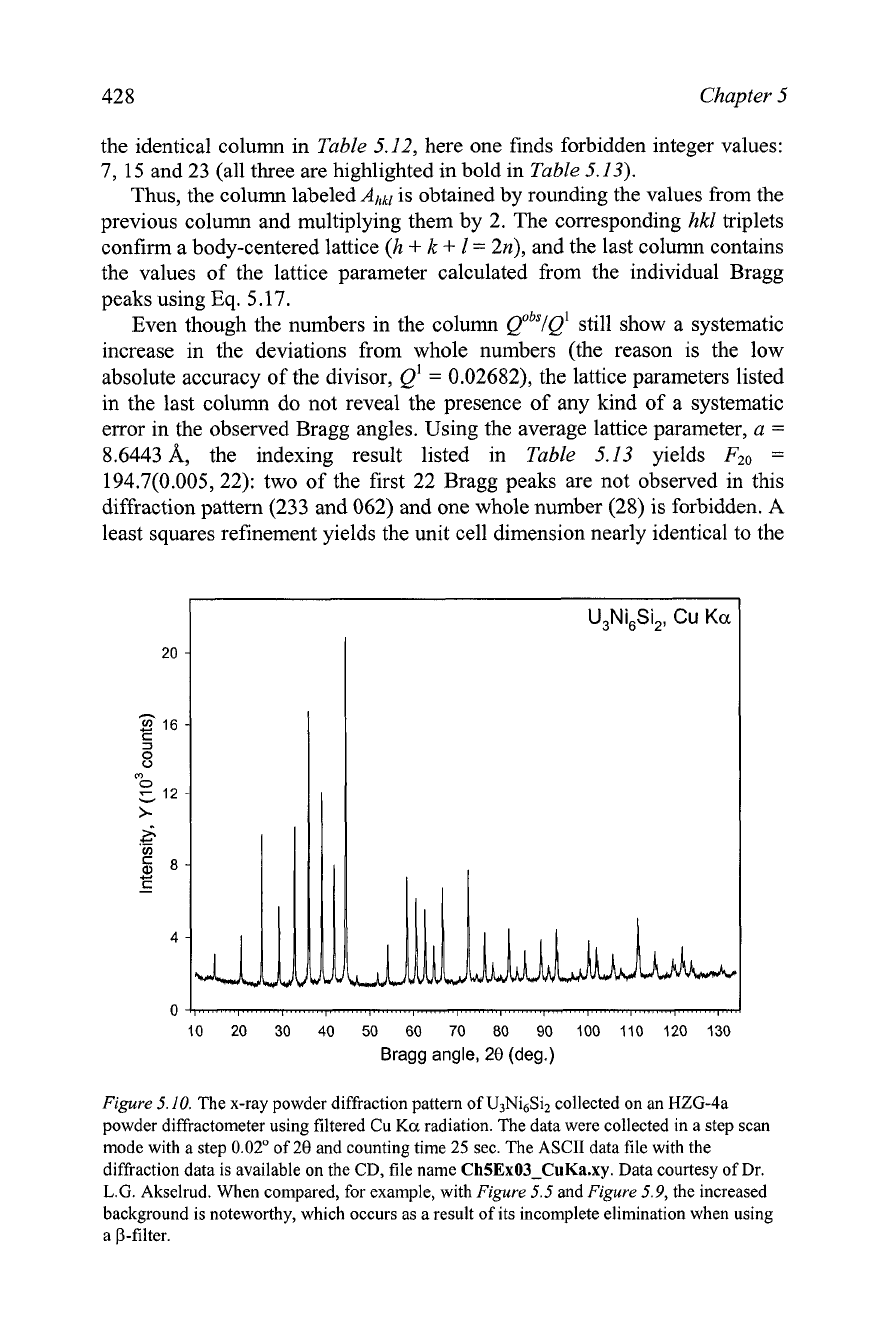
The second example is shown in

Figure

5.10 and

Table

5.13. The

observed Bragg peak positions were determined using a profile fitting

procedure and the least squares standard deviations in the observed Bragg

angles did not exceed 0.003" of 28. Considering the results shown in

Table

5.13, the column labeled

QObS/~'

contains nearly whole numbers, but unlike

42 8 Chapter

the identical column in Table 5.12, here one finds forbidden integer values:

and

(all three are highlighted in bold in Table 5.13).

Thus, the column labeled

Ahkl

is obtained by rounding the values from the

previous column and multiplying them by 2. The corresponding hkl triplets

confirm a body-centered lattice (h

2n), and the last column contains

the values of the lattice parameter calculated from the individual Bragg

peaks using

Eq.

5.17.

Even though the numbers in the column

Q"~~IQ'

still show a systematic

increase in the deviations from whole numbers (the reason is the low

absolute accuracy of the divisor,

0.02682), the lattice parameters listed

in the last column do not reveal the presence of any kind of a systematic

error in the observed Bragg angles. Using the average lattice parameter, a

8.6443

the indexing result listed in Table

5.13

yields

F2,,

194.7(0.005,22): two of the first 22 Bragg peaks are not observed in this

diffraction pattern (233 and 062) and one whole number (28) is forbidden.

least squares refinement yields the unit cell dimension nearly identical to the

I0 20 30 40 50 60 70 80 90 100 110 120 130

Bragg angle,

(deg.)

Figure

5.10.

The x-ray powder diffraction pattern of U3Ni6Si2 collected on an HZG-4a

powder diffractometer using filtered Cu

radiation. The data were collected in a step scan

mode with a step 0.02" of 20 and counting time 25 sec. The ASCII data file with the

diffraction data is available on the CD, file name

ChSEx03-CuKa.xy.

Data courtesy of Dr.

L.G. Akselrud. When compared, for example, with

Figure

5.5

and

Figure

5.9,

the increased

background is noteworthy, which occurs as a result of its incomplete elimination when using

a p-filter.

Unit cell determination and rejkement

429

average value shown above and results in a negligible zero shift correction.

leave the least squares refinement as an exercise to the reader.

Table 5.13.

Example of the

ab initio

indexing in the cubic crystal system using first

Bragg

peaks present in the pattern shown in

Figure

5.10.

Excel spreadsheet file

ChSEx03 BodyCenteredCubic.xls

is available on the

CD.

r/ro

2eobS

FWHMO~"

obs

obsl

Ahkl

hkl

Standard deviation

0.0021

Bragg angles are listed for the location of the

Ka,

component in the doublet,

1.540593

5.8

Tetragonal and hexagonal crystal systems

The quadratic form of Eq. 5.2 in the hexagonal crystal system is found in

Eq. 5.4 and its analogue in the tetragonal crystal system is

Following the approach illustrated using Eqs. 5.1 1 to 5.13 and

maintaining similar notations, Eqs. 5.4 and 5.18 can be written as

430

Chapter

where Qhkl

d*2hkl

l~d~~~~, Athk

(h2

k2),

~~hk

(h2

k2) and Cl

and noting that in the hexagonal crystal system a*

21~43. Hence, positions

of Bragg peaks found in the diffi-action patterns of materials that belong to

either the tetragonal or hexagonal crystal systems can be represented by the

following series of simultaneous equations, where Athk and

~~hk

are

substituted by Ahk:

The solution of Eq. 5.20 could be found after calculating all possible

differences between the observed pairs of Qhkl. This leads to the following

series of equations:

As follows from Eq. 5.2 1, when two Bragg peaks have the same value of

I, e.g. hikiO and hjkjO, or hikil and hjkjl, or hiki2 and hjkj2 and so on, the

resulting difference is only a function of Ahk and a*:

(5.22)

Qh,,,

Qhjkj,

(Ahiki

Ah],,

Similarly, when h and k are identical but 1 is different, e.g. Olli and 014,

or 1 1 li and 1 1 4, or 1 21i and 124, and so on, some of the equations in 5.2 1 are

transformed into:

Unit cell determination and refinement

43 1

Solving the indexing problem becomes a matter of identifying the

differences that result in whole numbers when divided by a common divisor

(a*2

and

c*~,

respectively). The expected whole numbers are shown in

Table

5.14 through

Table

5.16 for several small

and

It only makes sense to

consider these small values because successful indexing is critically

dependent on the availability of low Bragg angle peaks, which usually have

small values of indices.

The resulting whole numbers, expected as multipliers for the differences

in Q-values given by Eq. 5.23

(Table

5.14), are dissimilar from those

expected for Eq. 5.22

(Table

5.15 and

Table

5.16), and this property is used

to distinguish between

c*'

and

a*'.

Given the background considered above, the indexing of experimental

powder diffraction data assuming tetragonal or hexagonal symmetry may be

carried out using the algorithm illustrated in

Figure

5.11. First, all possible

differences between the observed Q-values are computed for several low

Bragg angle peaks. Second, the array of the obtained differences is analyzed

to find the most frequently occurring small values. Third, the found values

are tested with respect to whether or not the indexing of all observed Bragg

peaks is possible assuming that one of the quantities is and another is

c*~.

If the indexing is successful, both the crystal system and lattice

parameters are determined. If not, the found small values can be tested after

they have been divided by a whole number, usually between 2 and

Again,

if indexing is possible, the problem is solved but if the indexing is

impossible, one or both found small values suspected as

a*2

and

c*~

should

be discarded and the search for a suitable pair of

a*2

and

c*~

continues.

When all potential candidates have been tested and no solution has been

found, then likely the assumption of tetragonal or hexagonal symmetry is

wrong, or the powder diffraction data contain impurity Bragg peaks at low

angles, which makes reasonable indexing impossible.

Table

5.14.

Possible values of integer multipliers for the differences defined in

Eq.

5.23 for

both tetragonal and hexagonal crystal systems