Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials

Подождите немного. Документ загружается.

432

Chapter

Table

5.15.

Possible values of integer multipliers for the differences defined in

Eq.

5.22

for

the tetragonal crystal system

(00);

Ahk

(01);

dlzk

1 (I I);

Ahk

2 (02);

Akk

(12);

Ahk

(00);

Ahk

(01);

Ahk

1 1

(II);Ahkx2

(02);

Ahk

(12);

Ahk

Table

5.16.

Possible values of integer multipliers for the differences defined in

Eq.

5.22

for

the hexagonal crystal system

(00);

Ah,=

0 (01);

Ah,=

(02);

Ah,=

(12);

Akk=

(00);

Ahk

0 1

(01);

Ahk

1 2

(1 1);

Ahk

(02);

Ahk

small

It'

NO\

No but more suspects present

Yes Yes

Determine Refine lattice

Stop, stop,

indexing

crystal system parameters

different crystal

complete

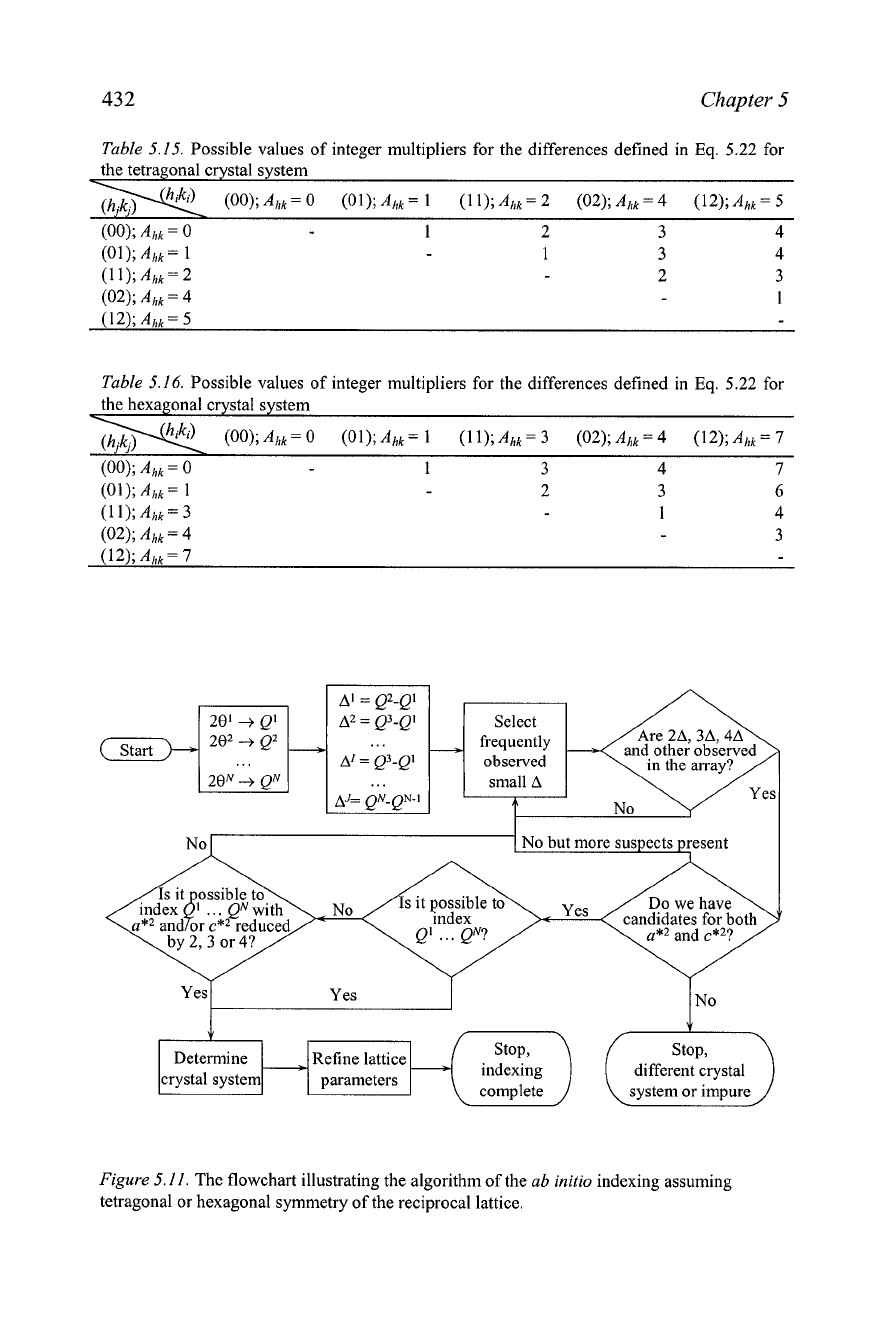
Figure

5.11.

The flowchart illustrating the algorithm of the

initio

indexing assuming

tetragonal or hexagonal symmetry of the reciprocal lattice.

Unit cell determination and refinement

433

5.8.1

Indexing example: LaNi4.85Sn0.15

We will illustrate the use of the technique described above by indexing

the powder diffraction pattern of LaNi4.85Sno.ls

(Figure

5.5

and

Table

5.1).

Note that in the process we make no assumptions about the exact symmetry

of the material except that we suspect that it may be either tetragonal or

hexagonal.

our indexing attempt we will limit all calculations to the first

seven observed Bragg peaks excluding the weak impurity peak observed at

44.21

as shown in

Table

5.17.

The observed Bragg angles as

determined directly from a profile fitting procedure are employed without

correcting for any kind of a systematic

err0r.l

Table

5.17.

Relative integrated intensities (Illo), Bragg angles and full widths at half

maximum (FWHM) of first eight Bragg peaks observed in the LaNi4,85Sno.15 powder

diffraction pattern, see

Figure

5.5.

The impurity Bragg peak shown using a strike-through

font has been excluded from the indexing attempt.

Illo

(deg)a FWHM (deg) IIIo

(deg)a FWHM (deg)

20 20.288 0.070 3 94 41.285 0.082

43 22.105 0.077 1000 42.272 0.085

513 30.198 0.076

4-8

0499

305 35.548 0.078 274 45.130 0.106

Bragg angles are listed for the position of the

Ka,

component in the characteristic Cu Ka

spectrum,

1.540593

The values of Bragg angles listed in

Table

5.17

have been converted into

the Q-values using

Eq.

5.3.

Possible differences

(Eq.

5.21)

have been

calculated and listed in

Table

5.18.

They are sorted and analyzed as shown in

Table

5.19.

The first column in this table includes the Q-values of the seven

observed Bragg peaks (in

bold)

in addition to all calculated differences.

Table

5.18.

Differences in Q-values for the first seven observed Bragg peaks in the powder

diffraction pattern of LaNi 85Sno,15.

0.0523 0.0619 0.1144 0.1570 0.2095 0.2191 0.2482

0.0523

0.0097 0.0621 0.1048 0.1572 0.1668 0.1959

0.0619

0.0524 0.0951 0.1475 0.1572 0.1862

0.1 144

0.0427 0.0951 0.1048 0.1338

0.1570

0.0524 0.0621 0.0911

0.2095

0.0097 0.0387

0.2191

0.0290

Although the presence of a systematic error may, in general, hinder an indexing attempt,

neglecting a small zero shift error in this case (see

Table

5.6)

is forgivable because only a

small region of Bragg angles (from

45' 20

)

is employed. When larger arrays of data

are included in an

initio

indexing, they should be corrected for all known systematic

errors, if any, for example by employing an internal standard.

434

Chapter

Table

5.19.

Illustration of the indexing of the first seven Bragg peaks observed in the powder

diffraction pattern of LaNi4,85Sno.15 using Eqs. 5.20 to 5.23.

Qob,,

Diff. Meana ~2~ ~3~ ~4~

a*', c*'

Eq. 5.19

QC~C

hkl

0.0097

0.0097 0.0097 0.0193 0.0290 0.0387

0.0290

0.0387

0.0427

0.1047

0.1571

0.2095

la*' 0.0524 010

91?'4fiZm

4c*' 0.2481 002

All values in the table are listed with four digits after decimal point but the actual

computations were performed with a better accuracy.

Considering Eqs. 5.22 and 5.23,

Table

5.14 through

Table

5.16, and

Figure

5.11 it is quite clear that all computed differences should be analyzed

for the occurrence of nearly identical small values, which potentially may

correspond to the differences resulting in

a*2

and

c*~

or their whole

multiples. Once the repetitive numbers are found, the next step is to find out

whether or not the array of differences and observed Q-values contains

whole multiples or whole fractions of the found quantities. The tested whole

numbers should be correlated with

Table

5.14 through

Table

5.16.

The initial candidate in the first column of

Table

5.19 is 0.0097, which

occurs twice. The average and the results of its multiplication by

and

the simplest whole numbers that are present in

Table

5.14 through

Table

5.16

are shown in columns 2,

4 and

If the computed average

corresponds to either

a*2

c*~

then these products should also be often

Unit cell determination and rejnement

435

observed in the array combining both the differences and observed Q-values.

As seen from Table 5.19, this is not the case since only one occurrence of

triple and quadruple multiples of the suspected value are found, and 0.0097

as a candidate for

a*2 or c*~ is dismissed as unsuitable. Furthermore, this

value appears too small because it results in d

10 A, which is too large

considering the simplicity of the powder diffraction pattern (Figure 5.5).

The next possibility is 0.0524, which occurs three times for the

differences between pairs of first seven observed Bragg peaks. Not only this

value is itself more frequently occurring than any other smaller quantity

found in the table, but when multiplied by two it yields 0.1047, which occurs

in the array twice

these nearly identical numbers are shown in italic.

Testing 0.0524 multiplied by three (0.1571) has three additional occurrences

(all are shown underlined). There is also one occurrence of 4~0.0524

0.2095, both are double underlined. Hence, this value seems to be an

excellent candidate for one of the reciprocal lattice parameters. After

consulting Table 5.14 through Table 5.16 it is clear that ~xc*~ is not

expected to be seen but

2~a*~ should be observed quite frequently in both

the tetragonal and hexagonal crystal systems.

Proceeding in a similar fashion with the triple occurrence of the next

small value (the average is 0.0620) we find that the array of differences and

observed Q-values has no occurrences of 2~0.0620

0.1241 but both

3~0.0620

0.1861 and 4~0.0620

,Q..2481

have one occurrence in the table.

Hence, as follows from Table 5.14 the value of 0.0620 is an outstanding

candidate for

c*~.

The next step is to verify whether or not the found candidates for and

c*~ (both are shaded in Table 5.19) result in the complete indexing of the

existing seven Bragg peaks. By using Eq. 5.19, all observed Q-values are

nearly equal to the sums of

~a*~ and CC*~, where

and C are whole

numbers, which are listed in the corresponding column in Table 5.19 in bold.

Strictly speaking, the whole diffraction pattern should be indexed following

the same approach, but we leave this to the reader as an exercise.

At this point (or after the whole pattern has been indexed) the analysis of

the observed values of A enables one to establish whether we deal with the

tetragonal or hexagonal crystal systems. As seen in Table 5.19, the whole

multipliers of

a*2 are 1 and

and 3 is only possible in the hexagonal crystal

system for

1. After a simple calculation using the average values

of and c*~ listed in Table 5.19 we find approximate values of a and c as

5.046 and 4.015 A, respectively. A least squares refinement of the lattice

parameters using the entire array of indexed Bragg peaks obviously yields

the same lattice parameters as were established before (see Table 5.6).

It is worth noting that the considered example is relatively easy because

first, the lattice is primitive and second, there were no extinct Bragg

Chapter

reflections among the first seven observed diffraction maxima. If some

Bragg peaks are missing, then the list of the generated differences (column

in Table

5.19)

becomes incomplete and the task of identifying the quantities

corresponding to a*2 and c*~ becomes considerably more complex. This is

especially true when the material has a Bravais lattice other than primitive

since additional lattice translations cause multiple systematic absences in the

list of possible

hkl's.

any case, the final indexing should always be

checked by calculating one or more figures of merit after refinement of

lattice parameters, which for this pattern has been done above (see sections

5.5.1 and 5.5.2)

Automatic

initio

indexing algorithms

The complexity of finding a solution of the indexing problem increases

rapidly as the symmetry of the lattice decreases. For instance, in the

orthorhombic crystal system the reciprocal unit cell dimensions, which affect

the governing reciprocal lattice equation

(Eq.

5. l), depend on three unknown

parameters (a, b and

c),

while in the monoclinic and triclinic crystal systems

the number of unknown parameters becomes four (a, b,

and p) and six (a,

b, c, a,

and

y),

respectively. As a result, manual indexing of low-symmetry

powder diffraction patterns becomes extremely difficult and time

consuming. Therefore, automatic indexing using various algorithms and

software is essential in the case of low symmetry. The use of computers also

speeds up high symmetry cases, and at the end, allows one to perform a

comprehensive search for indexing solution in all crystal systems.

The solution of the indexing problem can be found using several different

computational algorithms, which have been realized in a variety of automatic

indexing programs. All of them use one of the two fundamentally different

approaches to the ab initio indexing by treating either direct space

parameters

(i.e. unit cell dimensions) or reciprocal space parameters (i.e.

reflection indices) as free variables in order to describe all or almost all

observed diffraction peaks using a reasonable crystal lattice.

The first approach employs unit cell dimensions varying with a certain

increment within certain limits.

attempt to index the entire diffraction

pattern is made after every incremental step in lattice parameters. The

increments depend on both the accuracy and complexity of the diffraction

pattern but -0.01

for the unit cell edges (a, b and c) and -0.1" for the

angles (a,

and

should be sufficient in most cases.

The maximum size of the unit cell edges can be estimated from the d-

spacing of the first Bragg peak

(dm,,) observed in the diffraction pattern.

the majority of low symmetry cases (triclinic through orthorhombic crystal

systems), the maximum size of the unit cell edge should not exceed 2dm,,,

Unit cell determination and reJinement

while in the high symmetry cases it should be set at

(tetragonallcubic) to 6

(hexagonalltrigonal)

dm,.

When indexing superlattices, in which many

possible reflections are missing, higher limits on the maximum unit cell

dimensions may be required.

This is the simplest but also the slowest indexing method. Obviously,

each crystal system should be tested separately, as the number of free

variables has a critical influence on the computation time. For example, a

total of

lo6 unit cells must be checked assuming a tetragonal or hexagonal

crystal system with unit cell dimensions in the range between 2 and 22

using 0.01

increment. In a triclinic crystal system, with unit cell edges

between 2 and 12

and angles between 90 and 120•‹, a total of 2.7~10'~

combinations should be tested using 0.01 and 0.1" increments,

respectively. Assuming that 1,000,000 unit cells can be tested in 1 second,'

an unrestricted and exhaustive search in the tetragonal or hexagonal case will

take

-4

seconds, but one will have to wait nearly 860 years to test all

possible combinations and see the answer in a triclinic crystal system.

Modem high-speed computers can handle the problem in high symmetry

cases, especially taking into account that other restrictions are applicable.

For example, the maximum expected unit cell volume can be evaluated

from

the density of diffi-action peaks observed in a certain range of Bragg angles.

Furthermore, the following additional restrictions can be imposed: in the

monoclinic crystal system

c and in the orthorhombic and triclinic crystal

systems a

c, because in these cases the solution is invariant to a

permutation of unit cell edges, except for the need to convert to a standard

setting after the indexing was judged successful.

The most effective is the reciprocal space approach, in which several low

Bragg angle peaks are chosen as a basis set, and then an exhaustive

permutation-based assignment of various combinations of hkl triplets to each

peak fkom the basis set is carried out. Index permutation algorithms are more

complex in realization than direct space algorithms but the former are many

orders of magnitude faster than the latter.' This occurs because the indices of

This assumption is unrealistic using even the most powerful single processor

available

in late 2002. A more rational estimate is between -lo2 and -lo3 unit cells per second for a

well optimized computer code.

Consider a triclinic crystal system, where a minimum of six independent Bragg reflections

are required to determine the unit cell. Assuming that the maximum value of each of the

three indices is

and recalling that two of them should vary from

-1

(see

Table

5.7),

total number of possible combinations for one Bragg reflection is 3x3~2

[the set

(000) cannot be observed and is excluded from the consideration]. In an exhaustive search

without imposing any limitations, a total of

2.4~10' combinations among all six

reflections result. This represents about

orders

(!)

of magnitude reduction in the

computation time when compared to the mentioned above unrestricted exhaustive search

in direct space. The same example also highlights the critical role of the lowest Bragg

Chapter

low Bragg angle peaks, which are varied, are three relatively small integers.

Today, index permutation is the most common technique used in various

indexing computer programs and it will be discussed in this book.

The reciprocal space indexing can be implemented in several different

ways. Two of them are trial-and-error and zone search methods. The first

one is more efficient in high symmetry crystal systems (from cubic to

orthorhombic) but becomes slow for low symmetry crystal systems

(especially triclinic), while the second method works quite effectively and is

fast with low symmetries (from triclinic to orthorhombic).

5.9.1

Trial-and-error method

The trial-and-error method is based on assigning indices to a minimum

required number of low Bragg angle peaks

the so-called basis set. The

minimum number of peaks in the basis set is equal to the number of the

individual unit cell parameters, which varies from 1 to

depending on the

crystal system. The values of indices in the triplets vary between certain pre-

selected minimum and maximum values of h,

and I. Each permutation is

followed by the determination of a trial unit cell and by an attempt to index

-10 to 30 consecutive reflections at higher Bragg angles in the resulting unit

cell. Successful solutions, i.e. those, which produce the fully or almost fully

indexed diffraction pattern, are stored along with the computed figure(s) of

merit for further analysis and automatic or manual selection of the best

indexing solution.

The success of this approach is critically dependent on the selection of

the basis set, which generally should contain more Bragg peaks than the

number of the unknown unit cell dimensions. Potential caveats include but

are not limited to the following: the selected basis set contains reciprocal

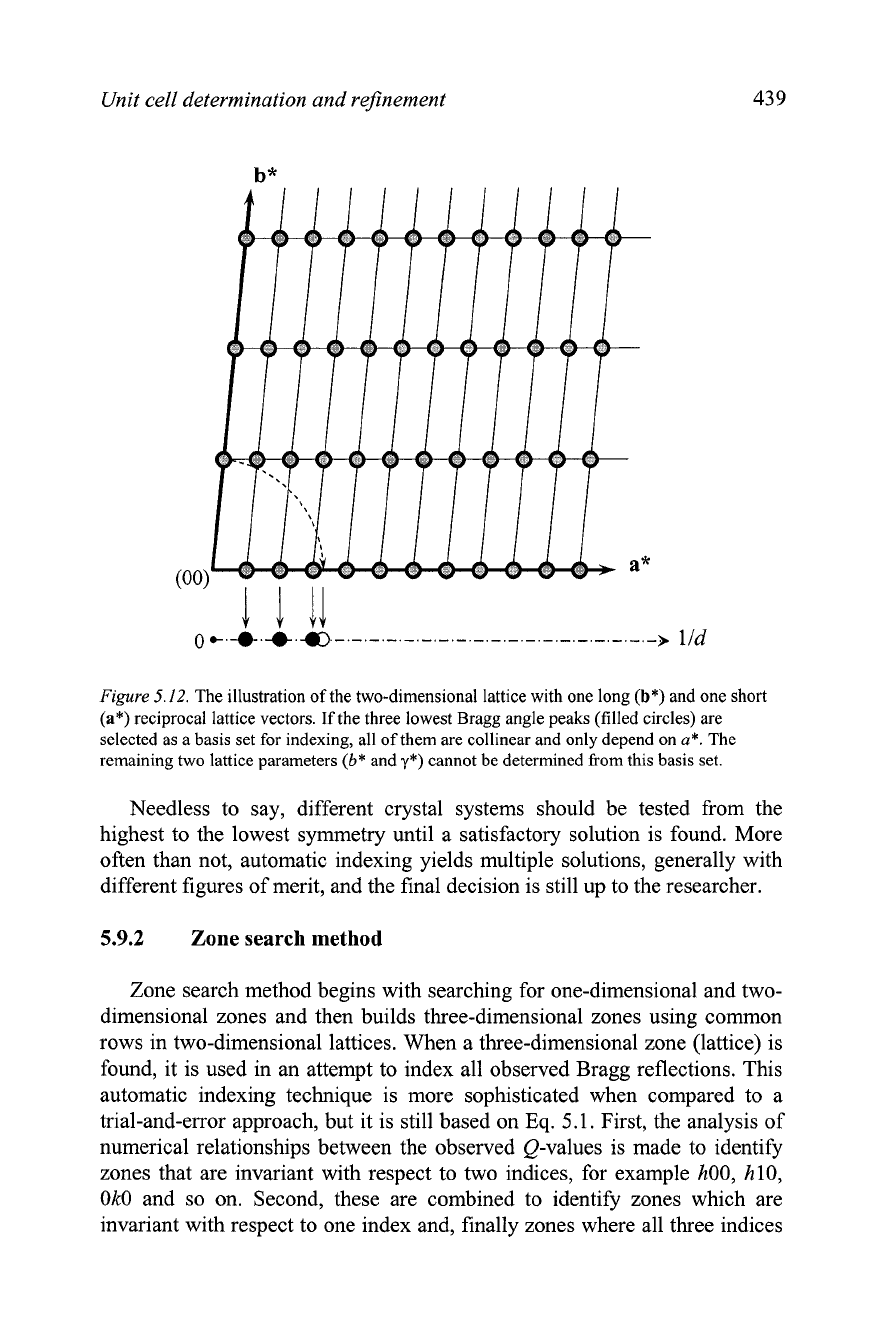
vectors which are collinear or coplanar (see Figure

5.12);

there is one or

more impurity peak(s) in the basis set or in the list of Bragg peaks included

into the consideration during the indexing attempt, and improper selection of

the minimum and maximum h,

and 1 values for index permutations.

The exhaustive permutation technique may be improved by eliminating

collinear reciprocal lattice vectors from the basis set, which can be done by

analysis of the relationships between the observed low Bragg angle

Q-

values. As follows from Eq. 5.1, when two different lld

are related to

one another by a whole multiplier, there is a high probability that the two are

collinear, and only the smallest is usually retained in the basis set.

angle reflections in finding a solution of the indexing problem: when the maximum index

to be considered is increased to

the total number of combinations to be tested in an

unrestricted exhaustive search rises to

-1.6x10",

and it becomes

-2.1~10'~

when the

maximum value of index increases to

Unit cell determination and rejkement

Figure

5.12.

The illustration of the two-dimensional lattice with one long

(b*)

and one short

(a*)

reciprocal lattice vectors. If the three lowest Bragg angle peaks (filled circles) are

selected as a basis set for indexing, all of them are collinear and only depend on

a*.

The

remaining two lattice parameters

(b*

and

y*)

cannot be determined from this basis set.

Needless to say, different crystal systems should be tested from the

highest to the lowest symmetry until a satisfactory solution is found. More

often than not, automatic indexing yields multiple solutions, generally with

different figures of merit, and the final decision is still up to the researcher.

5.9.2

Zone search method

Zone search method begins with searching for one-dimensional and two-

dimensional zones and then builds three-dimensional zones using common

rows in two-dimensional lattices. When a three-dimensional zone (lattice) is

found, it is used in an attempt to index all observed Bragg reflections. This

automatic indexing technique is more sophisticated when compared to a

trial-and-error approach, but it is still based on Eq. 5.1. First, the analysis of

numerical relationships between the observed Q-values is made to identify

zones that are invariant with respect to two indices, for example hOO, h10,

OM)

and so on. Second, these are combined to identify zones which are

invariant with respect to one index and, finally zones where all three indices

440

Chapter

in the triplets vary independently are found and analyzed. To a certain

extent, zone searching resembles the algorithm described above for the

manual indexing in the tetragonal and hexagonal crystal systems; for

example, zones that are invariant to both

and

should satisfy Eq. 5.24.

d;,,

ha*

const

The zone search indexing method does not require an assumption about

the crystal system and therefore, it results in a primitive lattice in most cases.

When the lattice is confirmed by the subsequent indexing of all observed

Bragg peaks, it shall be converted to one of the 14 standard Bravais lattices.

The latter is achieved in a process known as the reduction of the unit cell.

5.10

Unit cell reduction algorithms

Low symmetry unit cells can be selected in a variety of ways regardless

of which method was used to find the unit cell suitable to index the entire

diffraction pattern. For example, in the case of an orthorhombic crystal

system, all three vectors

and c can be permuted; in a monoclinic crystal

system, a, c and

&(a

c) can be switched in a setting with

90•‹,

while

in a triclinic case, lattice vectors may be selected in a number of different

ways.

order to compare and analyze different indexing solutions, the

lattice must be reduced to a certain unique, preferably standard form. It is

usually achieved by applying the following rules (which sometimes are

already incorporated in the indexing process itself by imposing specific

restrictions on the assigned indices):

the orthorhombic crystal system the unit cell dimensions should be

such that

the monoclinic crystal system,

c, assuming a standard setting with

as the unique axis.

the triclinic crystal system, the reduction becomes more complicated

due to possible multiple choices of the basis vectors in the lattice.

The first two reduction rules are normally employed only during the

indexing. They usually do not produce a standard choice of the unit cell

since at this stage the space group symmetry, and often even the lattice type,

are not involved. For example, in the orthorhombic space group symmetry

Pnma (a standard setting) the condition

c is not necessarily obeyed.

There are two broadly accepted methods of unit cell reduction. One of

them was introduced by Delaunay' and then applied to a transformation of a

Delaunay. Neue Darstellung der geometrischen Kristallographie.

Kristallogr.

84,

109 (1933).

Unit cell determination and refinement

randomly selected unit cell by 1to.I This technique is known as the

Delaunay-Ito method.

order to achieve complete standardization, a

different method should be employed in the reduction of the unit cell. This

approach, originally introduced by Niggli,' results in the so-called Niggli-

reduced unit cell.

5.10.1

Delaunay-Ito reduction

The Delaunay-Ito reduction is performed on three lattice vectors vl, v2

and v3, and a fourth vector, v4

-vl

v3 (an inverted body diagonal of a

parallelepiped) as shown in

Figure

5.13, left.

this figure, four vectors vi

are associated with the comers of a tetrahedron, while six scalar products,

vi.vj

lvillvjlcosao (for i

j),

are associated with the edges of the same

tetrahedron. The unit cell is considered reduced when angles

between

each pair of vectors vi are greater than or equal to

90'

and therefore, all

scalar products

sij

are negative or zero.

The reduction is achieved by changing the sign of any scalar product that

is greater than zero, simultaneously with modifying other relevant

parameters of the tetrahedron as shown in

Figure

5.13, right. This procedure

is equivalent to adding vectors and is repeated until all scalar products, so,

become negative or zero.

Figure

5.13.

The schematic of Delaunay-Ito transformation. Left

the four unit cell vectors

(v,, vz, v3

and

-vI-vt-v3)

are associated with the comers of the tetrahedron, while the six

scalar products between the corresponding pairs of the vectors

(s12

through

sS4)

are linked to

the edges of the tetrahedron. Assuming that

s12

the transformation is carried out as shown

on the right: the sign of

slz

is changed; its value is subtracted from that on the opposite edge

and added to those on all adjacent edges; the direction of

(or

vz)

is reversed and the new

vectors

vt3

and

vt4

are determined as

v3+vl

and

v4+v1

(or

V3+V2

and

v4+vZ,

respectively).

Ito, A general powder x-ray photography, Nature

164,755

(1949).

Niggli. Krystallographische und strukturtheoretische Grundbegriffe. Band

Teil,

Handbuch der Experimentalphysik, Akademische Verlagsgesellschafi,

108

928).