Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials

Подождите немного. Документ загружается.

462

Chapter

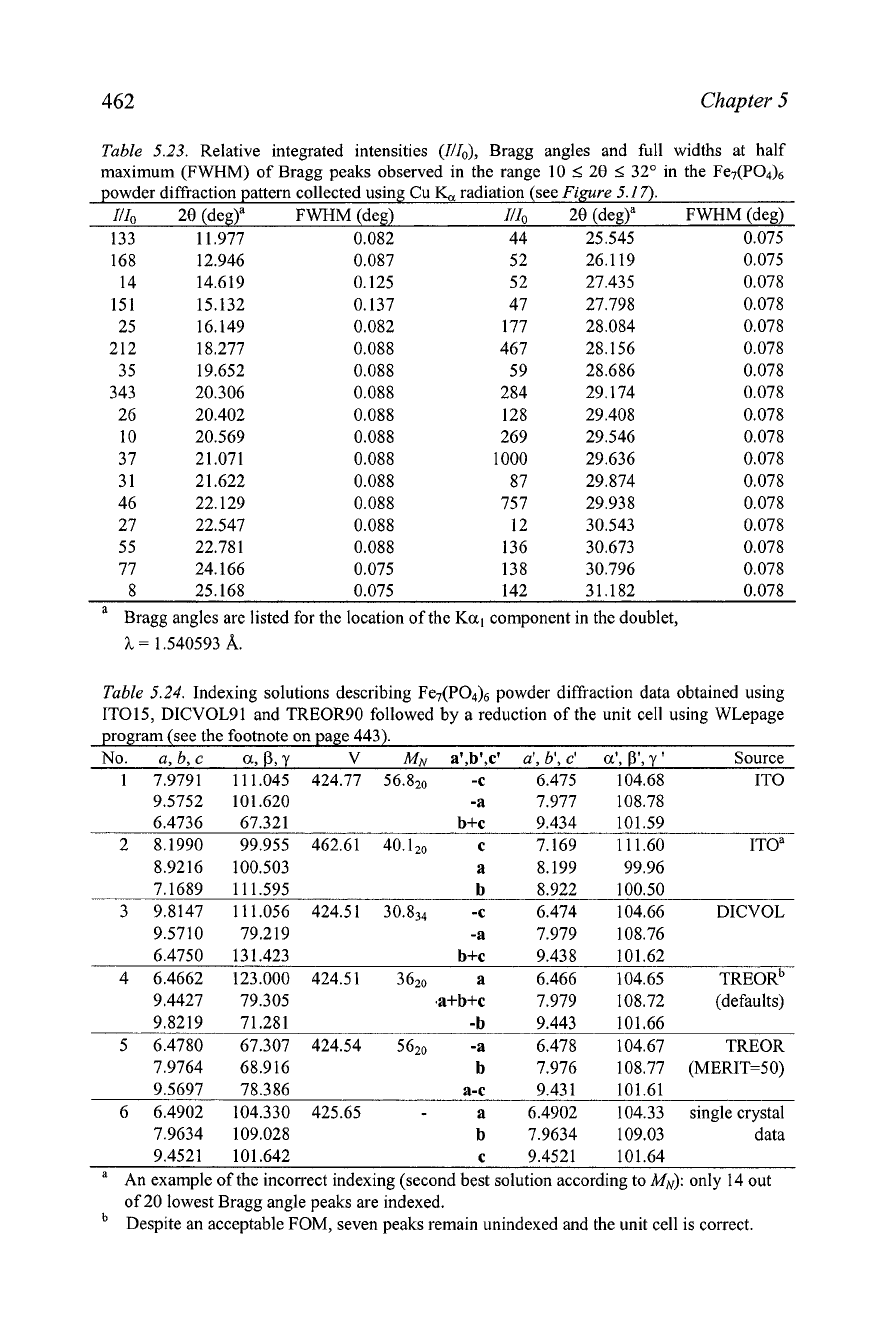
Table

5.23.

Relative integrated intensities (III,), Bragg angles and full widths at half

maximum

(FWHM)

of Bragg peaks observed in the range 10

32' in the Fe7(P04)6

powder diffraction pattern collected using Cu

radiation (see

Figure

5.17).

Illo 20 (deg)a FWHM (deg) IIIo 20 (deg)" FWHM (deg)

1 1.977 0.082 44 25.545 0.075

343 20.306 0.088 284 29.174

26 20.402 0.088 128 29.408

10 20.569 0.088 269 29.546

37 21.071 0.088 1000 29.636

3 1 21.622 0.088 87 29.874

46 22.129 0.088 757 29.938

27 22.547 0.088

12 30.543

5 5 22.781 0.088

136 30.673

77 24.166

0.075

138 30.796

8 25.168 0.075 142 31.182

Bragg angles are listed for the location of the

Ka,

component in the doublet,

1.540593

Table

5.24.

Indexing solutions describing Fe7(P04)6 powder diffraction data obtained using

IT015, DICVOL91 and TREOR9O followed by a reduction of the unit cell using WLepage

program (see the footnote on page 443).

No.

a, b,

V MN

a',bf,c'

a', b',

a',

(3',

Source

1 7.9791 11 1.045 424.77 56.82,

-C

6.475 104.68 IT0

9.5752 101.620

-a

7.977 108.78

8.9216 100.503

8.199 99.96

7.1689 111.595

8.922 100.50

3 9.8147 111.056 424.51 30.S34

-C

6.474 104.66 DICVOL

9.5710 79.219

-a

7.979 108.76

6.4750 13 1.423

b+c

9.438 101.62

4 6.4662 123.000 424.51 3620

6.466 104.65 TREOR~

9.4427 79.305

.a+b+c

7.979 108.72 (defaults)

9.8219 71.281

-b

9.443 101.66

5 6.4780 67.307 424.54 5620

-a

6.478 104.67 TREOR

7.9764 68.916

7.976 108.77 (MERIT=50)

9.5697 78.386

a-c

9.431 101.61

6 6.4902 104.330 425.65

6.4902 104.33 single crystal

7.9634 109.028

7.9634 109.03 data

9.4521 101.642

9.4521 101.64

An example of the incorrect indexing (second best solution according to MN): only 14 out

of 20 lowest Bragg angle peaks are indexed.

Despite an acceptable FOM, seven peaks remain unindexed and the unit cell is correct.

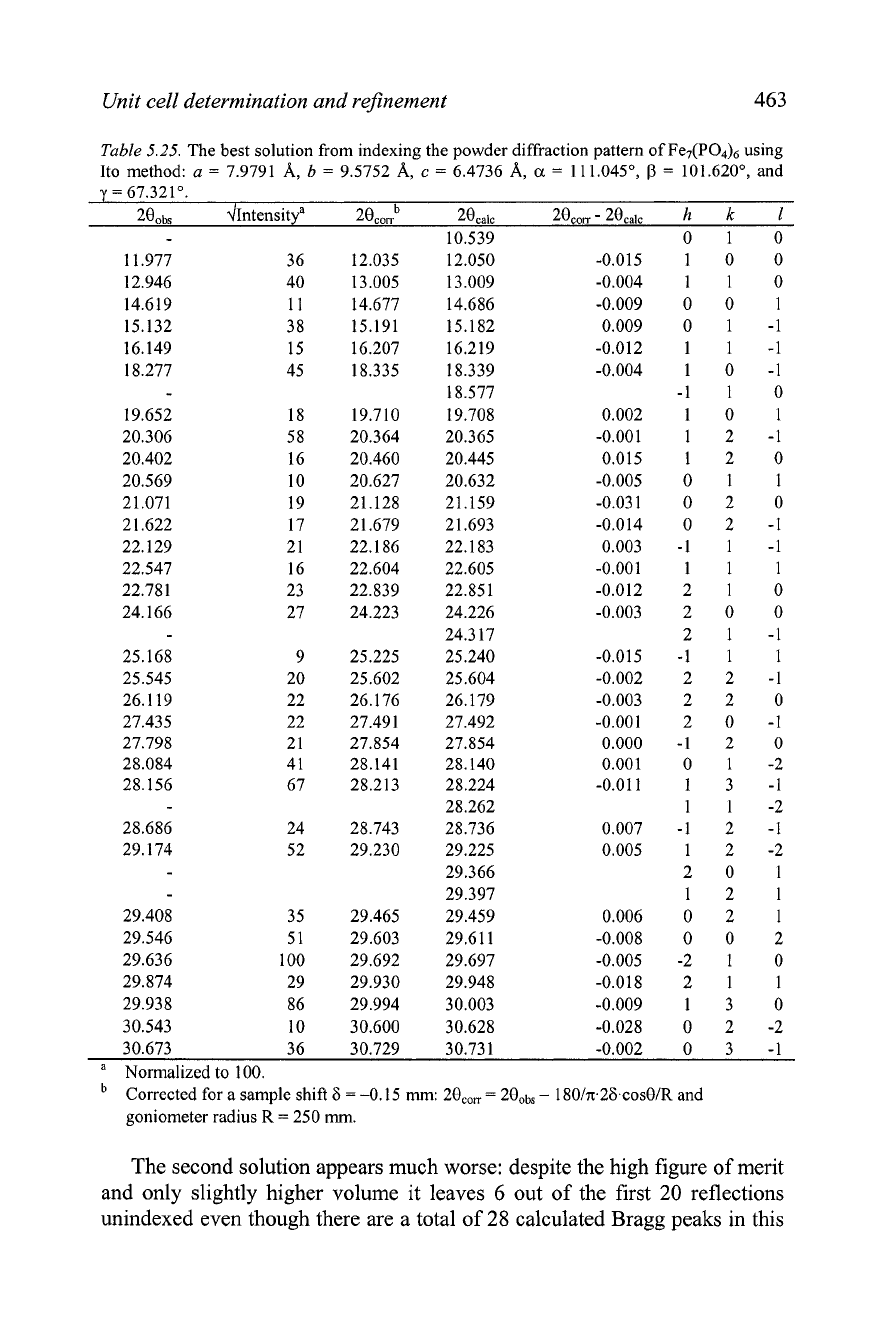
Unit cell determination and reJinement

463

Table

5.25.

The best solution from indexing the powder diffraction pattern of Fe7(P0& using

Ito method:

7.9791

9.5752

6.4736

cc.

111.045",

101.620•‹, and

30.673 36 30.729 30.731 -0.002 0 3 -1

Normalized to 100.

Corrected for a sample shift

-0.15

mm:

20,,,

2Ook

180/n~26.cosOlR and

goniometer radius

250

mm.

The second solution appears much worse: despite the high figure of merit

and only slightly higher volume it leaves

out of the first

reflections

unindexed even though there are a total of

calculated Bragg peaks in this

464

Chapter

range of angles. Other solutions have much lower figures of merit, higher

volume and too many unindexed peaks along with a large number of

calculated Bragg reflections that are unobserved.

Some of the unreliable solutions can be eliminated by decreasing the

tolerances in

28 for zone searches. However, there is a danger of choosing a

tolerance that is too low, and by using it, the true solution can be missed. To

avoid this, the tolerance should be reduced gradually and only when

excessive amounts of different and unreliable solutions emerge.

our

example, the tolerance that was set by default between 3 and 4 appears to be

a good choice.

Table

5.24 also contains the results of triclinic indexing using the

DICVOL and TREOR algorithms. With all crystal systems tested, DICVOL

results in a single solution, shown in the third row. All reflections were

indexed and the figures of merit are quite high:

M34

30.8 and

F34

lO4.5(O.O08 1, 40). Employing TREOR with all parameters set to their

default value (except instruction TRIC

1) three solutions where found.

Two of them with unit cell volume of -800

have very low figures of

merit and leave many peaks unindexed. The third one has the same cell

volume (-424

A3)

as the earlier solutions, and is listed in row 4. This

solution has 6 out of 34 Bragg reflections unindexed, which is due to the low

accuracy of the determined unit cell. To check other possible solutions, the

keyword MERIT

50 was inserted in the input data file. This modification

results in more than 20 different solutions with a unit cell volume of

-424

A3.

The best solution has all 34 reflections indexed, high figures of

merit, and it is listed in row

As is obvious from columns 2 and 3 in

Table

5.24, different indexing

algorithms result in different choices of the unit cell for the same lattice and,

therefore, unit cell reduction is especially important to compare the results in

triclinic symmetry. The unit cell dimensions, reduced using the

WLepage

program, are listed in

Table

5.24 in columns 6-8. Obviously, all of them are

represented by the same unit cell, except the incorrect solution shown in row

2. The triclinic unit cell was confirmed by a single crystal diffraction

experiment, as shown in row 6.

5.13

Precise lattice parameters and linear least squares

After the powder diffraction pattern has been successfully indexed, the

next step is to establish the unit cell dimensions with the highest possible

precision. By combining Eqs. 5.2 and 5.3 one can see that the errors in the

lattice parameters only depend on the errors in the measured Bragg angles

assuming that Miller indices and

are known exactly:

Unit cell determination and refinement

465

By differentiating the right hand side of Eq. 5.28 we find that the

absolute error in the interplanar distance, od, is a function of both the error

in Bragg angle, 08, and Bragg angle:

cos

o€l

2sin2

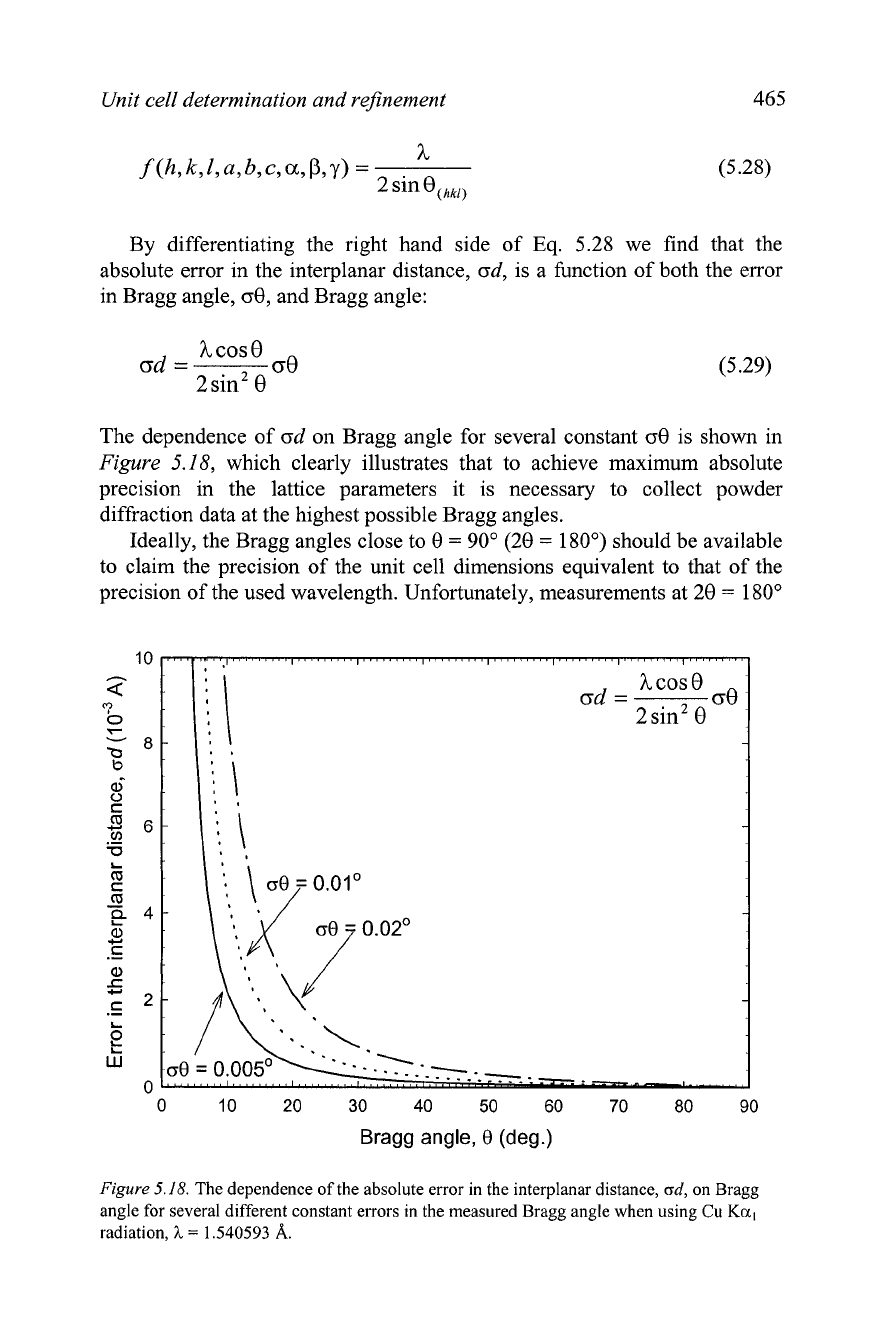
The dependence of od on Bragg angle for several constant o8 is shown in

Figure

5.18,

which clearly illustrates that to achieve maximum absolute

precision in the lattice parameters it is necessary to collect powder

diffraction data at the highest possible Bragg angles.

Ideally, the Bragg angles close to 8

90" (28

180") should be available

to claim the precision of the unit cell dimensions equivalent to that of the

precision of the used wavelength. Unfortunately, measurements at 28

180"

0 10 20 30 40 50 60

80 90

Bragg angle,

(deg.)

Figure

5.18.

The dependence of the absolute error in the interplanar distance,

od,

on Bragg

angle for several different constant errors in the measured Bragg angle when using

Ka,

radiation,

S40593

466

Chapter

are impossible and in most commercial powder diffractometers the highest

reachable Bragg angle is limited by

140 to 150'. Thus, in nearly every

instance, all available data are used to determine lattice parameters using

least squares refinement. The use of the least squares technique is fully

justifiable as it also allows one to refine the most critical corrections to the

observed Bragg angles that arise from the presence of systematic errors in

the experimental data due to sample displacement or zero shift.

5.13.1

Linear least squares

Assume that we need to find a solution of the system of

simultaneous

linear equations with m unknown parameters.

general form, this system of

equations can be represented as

allxl

a12x2

...

aImxm

a2,xl

a,,x2

...

a2,x,

anlxl

a,,x2

+...+

anmx,

a matrix and vector notation, Eq.

5.30

becomes

where

When

m, Eq.

5.30

has an infinite number of solutions with respect to

a set of

unknowns, and each particular solution depends on certain

assumptions which were made about the values of the remaining m

parameters. When

Eq.

5.30

has one exact solution, if it exists when

det(A)

On the other hand, when

the solution of Eq.

5.30

can be

obtained in two fundamentally different ways.

First, it is possible to randomly select m equations and find m parameters,

if any, that exactly satisfy each of the m selected equations. This solution,

Unit cell determination and refinement

467

however, will likely be far from the best for the remaining

equations

(e.g. see the varying lattice parameter determined

this way in

Table

5.12).

Second, it is possible to find vector

which would be the best solution

for all

existing equations using the least squares technique. The least

squares solution of Eq. 5.30 is obtained by rearranging it into the following

form

and then finding the minimum of the following function

@(x,,x,

,..

x,)

Ce2

The best solution of Eq. 5.33 (and Eq. 5.30) is found by calculating

partial derivatives of the function defined in Eq. 5.34 with respect to XI, x2,

x, and equating each to zero, which are the conditions of the minimum

x], x2,

. .

x,):

Obviously, Eq. 5.35 has a single solution, if any, since we replaced the

system containing

equations and

unknowns (Eqs. 5.30 and 5.33) with

the system that has the same number of equations as there are free

parameters. After calculating partial derivatives, grouping the coefficients

near the same xi and rearranging each of the equations, we get the following

equivalent of Eq. 5.35:

Chapter

The coefficients in the left hand side of Eq. 5.36 are nothing else than the

product of the transpose of matrix A (Eq. 5.3

and the matrix A itself, and

the coefficients in the right hand side of Eq. 5.36 can be represented as the

product of the transpose of matrix A and vector

(Eq. 5.3 1). Thus, letting

AT be the transpose of matrix A

Eq. 5.36 can be written in a matrix and vector notation as

Its solution (and simultaneously the least squares solution of Eq. 5.30) is

found from

where

(ATA)-' is the inverse of a square matrix, which is the product of AT

and A. Equations 5.35, 5.36 and 5.38 are identical and they represent

different notations of the so-called normal equations in the least squares

method. Two noteworthy properties of the elements of the normal equation

matrix (ATA) or, which is the same, the coefficients near the unknowns in

normal equations (Eq. 5.36) are:

The elements located on the main (principal) diagonal of the matrix are

always positive, and

The matrix is symmetrical with respect to the main diagonal.

Unit cell determination and refinement

469

5.13.2

Precise lattice parameters from linear least squares

We now consider the most general form of Eq. 5.28, i.e. that which

relates the unit cell dimensions, Miller indices, wavelength and Bragg angles

in the triclinic crystal system. In a quadratic form, it can be written as

2hkabc2 (cos

cos

cosy)

2hlab2c(cosacos

cos

4sin2

2kla 2bc(cos

cosy

cos

a)]

where

is the volume of the unit cell, which is given as

By comparing Eq. 5.40 with Eq. 5.30, it is easy to see that the linear least

squares technique is not directly applicable in this case since the former

equation is clearly non linear with respect to the unknowns (a,

and

y).

If, however, Eq. 5.40 is rewritten it terms of the reciprocal lattice

parameters

(h2a

+k2b

+12c *2 +2hka

cos

it becomes linear with respect to a different set of the unknowns:

where the new parameters,

Si,

are defined as follows:

Chapter

S12 =a*b*cosy*=

abc2 (cos

cos

cosy)

S13 =a*c*cosp*=

ab2c(cos a cosy

cosp)

'bc(cos cos

cos

S2,

b*c*cosa*=

By comparing Eq. 5.43 with Eqs. 5.30 to

5.32

it is easy to see that matrix

A and vector

are constructed as follows:

and that the least squares solution according to

Eq.

5.39 results in a vector

Unit cell determination and refinement

from which the unit cell dimensions of the direct lattice are calculated using

Eq. 5.44.

So far, we considered the application of a liner least squares technique in

the case when no systematic error has been present in the observed powder

diffraction data. However, as we already know, in many cases the measured

Bragg angles are affected by a systematic sample displacement or zero shift

error. The first systematic error affects each data point differently and

considering Eq. 3.4 (section

3-53, when a sample displacement error,

present in the data, Eq. 5.43 becomes

Eq. 5.48, R is the radius of the goniometer. The second systematic

error adds a small constant value,

600,

to each observed Bragg angle, which

results in the following equivalent of Eq. 5.43:

Both Eqs. 5.48 and 5.49 introduce one additional parameter in the least

squares refinement, i.e. sample displacement divided by the goniometer

radius,

SIR, or zero shift,

&go,

respectively. Regardless of the fact that the

contribution from both parameters is nonlinear, the linear least squares

technique can still be applied after the following simplifications.

From trigonometry, we know that