Pecharsky V.K., Zavalij P.Y. Fundamentals of Powder Diffraction and Structural Characterization of Materials
Подождите немного. Документ загружается.


sin(a
+
P)
=
sin
a
cos
P
+
cos
a
sin
P
sin
2a
=
2
sin
a
cos
a
Chapter
5
(5.50)
Hence
Recall that x, which represents an error in the Bragg angle, is usually
quite small, then cos2x
E
1,
sin2x
2
0 and sin2x
G
2x. Whence, Eq. 5.51 is
simplified to
By substituting the result obtained in Eq. 5.52 into Eqs. 5.48 and 5.49
they are transformed into
(S,, h2
+
sZ2k2
+
s3,12
+
2SI2hk
+
2S13hl
+
2S2,kl)
-
s
4
cos
8
sin
28
=
4sin2
8
R
h2 h
and
Matrix
A
is then modified to
h: k: 1; 2h,k1 2h,l, 2k,4
4 cos 8, sin 28,
h2
4 cos
8,
sin 28,
h; kt lZ2 2h2k2 2h212 2k212
h2
(5.55)

Unit cell determination and rejinernent
4
sin
28,
h: k:
1:
2h1k1 2h,Z1 2k111
h2
4
sin
28,
hi k:
1;
2h,k, 2h,l, 2knln
h2
to account for the sample displacement and zero shift errors, respectively,
and the least squares solution produces the following vectors
When the symmetry of the material is higher than triclinic, Eqs.
5.53
and
5.54 contain fewer unknowns and the least squares procedure is simplified.
The least squares technique described above assumes that each data point
(i.e. Bragg peak) is measured with the same experimental error and
therefore, equally contributes into the resulting solution that represents the
refined unit cell dimensions
andlor correction for a systematic error, if any.
When a realistic estimate of individual errors in Bragg angles is available, it

474
Chapter
5
is possible to adjust the contributions from the individual Bragg peaks to
reflect higher or lower precision in the determination of Bragg angles. This
is realized by introducing individual weights into the calculation of the
normal equations.
Thus, each row of matrix
A,
each element of vector
y
(see Eq. 5.32) and
each column of the transpose matrix AT (see Eq. 5.37) is changed by the
multiplier that is inversely proportional to the square root of the
experimental error in the corresponding experimental data point.
Alternatively, the weighted least squares solution may be expressed as
follows
where W is the square matrix representing individual weights for each of the
available
n
data points:
The standard uncertainties (or standard deviations) for each parameter
determined according to the least squares method are calculated from
where:
-
n
is the number of equations (Bragg peaks),
-
m
is the number of unknown parameters (from two to seven assuming
that sample displacement or zero shift error is always refined),
-
(A~wA)~~" is the corresponding diagonal element of the inverse
normal equation matrix,
-
wk
is the corresponding weight if any,
-
(Q:"
-
QT'")
is the difference between the observed and calculated
1
Id2.
Unit cell determination and refinement
475
There are many different stand-alone software programs available
through the International Union of Crystallography' or Collaborative
Computational Project No. 142 Web sites in addition to various
commercially available least squares utilities. We will illustrate the least
squares refinement of the lattice parameter of the La& compound, which
was fully indexed earlier, see
Table
5.12.
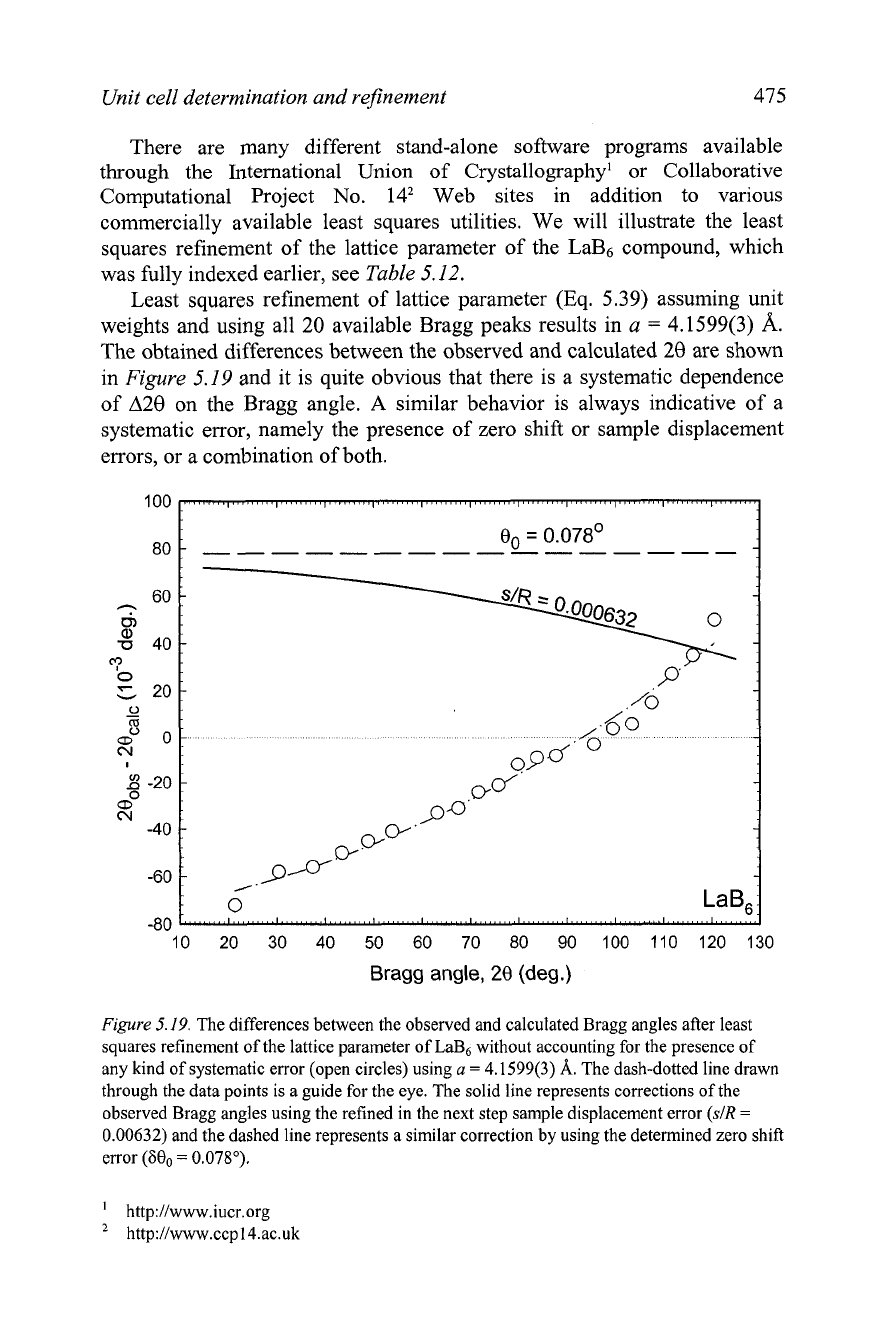
Least squares refinement of lattice parameter (Eq. 5.39) assuming unit
weights and using all 20 available Bragg peaks results in
a
=
4.1599(3)
A.
The obtained differences between the observed and calculated 28 are shown
in
Figure
5.19
and it is quite obvious that there is a systematic dependence
of A28 on the Bragg angle.
A
similar behavior is always indicative of a
systematic error, namely the presence of zero shift or sample displacement
errors, or a combination of both.
10 20 30
40
50 60 70 80 90 100 110 120 130
Bragg angle,
20
(deg.)
Figure
5.19.
The differences between the observed and calculated Bragg angles after least
squares refinement of the lattice parameter of LaB6 without accounting for the presence of
any kind of systematic error (open circles) using
a
=
4.1599(3)
A.
The dash-dotted line drawn
through the data points is a guide for the eye. The solid line represents corrections of the
observed Bragg angles using the refined in the next step sample displacement error
(SIR
=
0.00632) and the dashed line represents a similar correction by using the determined zero shift
error
(600
=
0.078").
476
Chapter
5
The fact that the difference between the observed and calculated Bragg
angles changes sign
(Figure
5.19),
is intrinsic to a least squares technique,
which simply minimizes the function defined in
Eq.
5.34. As a result, the
refined lattice parameter of La&,
a
=
4.1599(3) A, is far from its standard
value of
a
=
4.15695(6)
A.
When the sample displacement error has been
refined together with the lattice parameter, this yields
a
=
4.1583(1)
A
and
SIR
=
0.00632. On the other hand, when zero shift error is refined instead of
sample displacement, the resultant unit cell dimension becomes
a
=
4.1574(1)
A
and zero shift
6e0
=
0.078". The corresponding corrections of
the observed Bragg angles are shown in
Figure
5.19 and the respective sets
of differences between the observed and calculated Bragg angles are
depicted in
Figure
5.20.
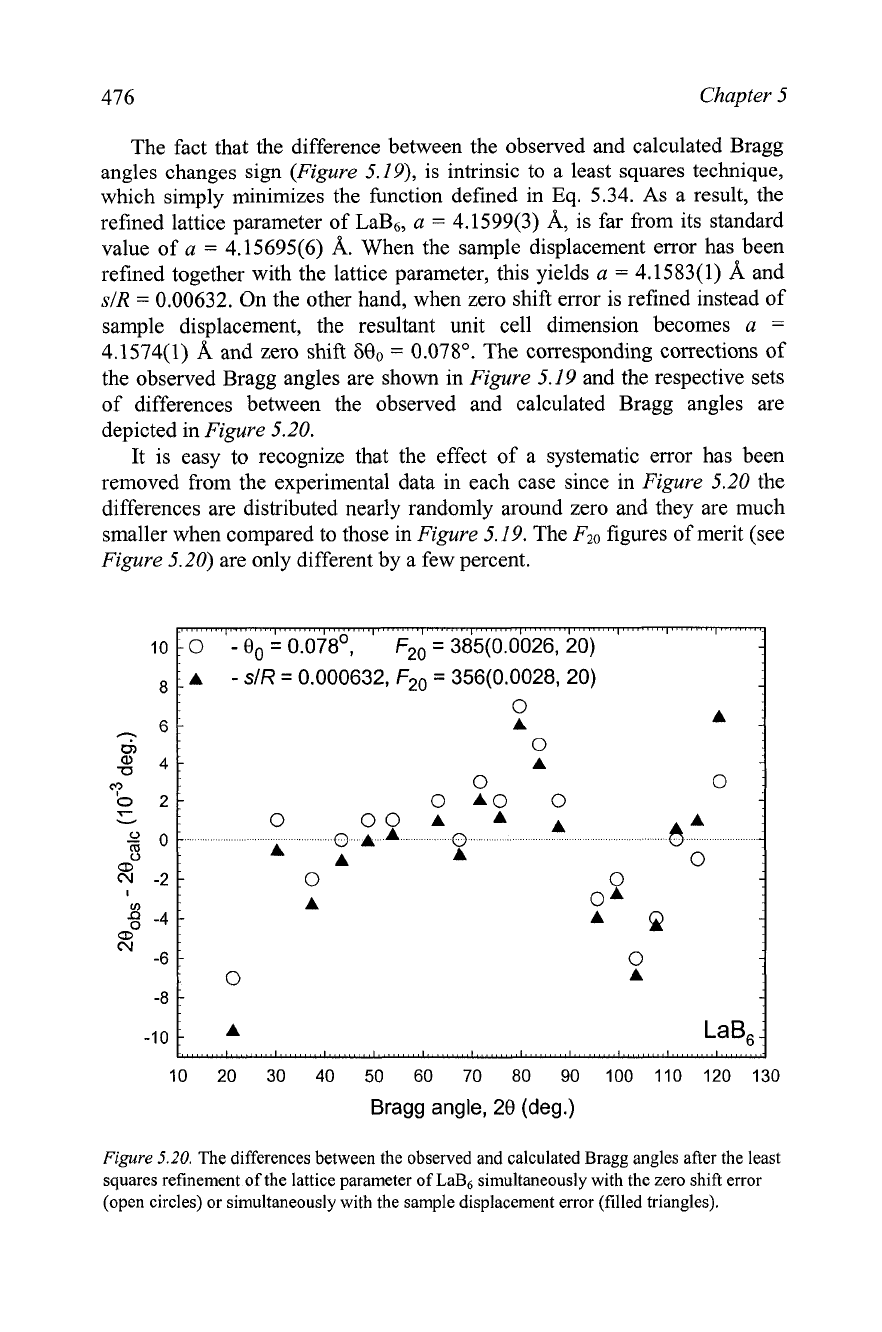
It is easy to recognize that the effect of a systematic error has been
removed from the experimental data in each case since in
Figure
5.20 the
differences are distributed nearly randomly around zero and they are much
smaller when compared to those in
Figure
5.19. The
F20
figures of merit (see
Figure
5.20) are only different by a few percent.
10 20 30 40 50 60 70 80 90 100 110 120 130
Bragg angle,
28
(deg.)
-8
-10
Figure
5.20.
The differences between the observed and calculated Bragg angles after the least
squares refinement of the lattice parameter of LaB6 simultaneously with the zero shift error
(open circles) or simultaneously with the sample displacement error (filled triangles).
7
:
A
LaB,
I
Unit cell determination and rejkement
477
However, if one compares the values of the lattice parameter obtained
when a different kind of a systematic error was assumed and accounted for
in the data, the difference between the two is statistically significant (4.1583
vs. 4.1574
A
for sample displacement and zero shift effects, respectively).
This is expected given the different contribution from different errors as seen
in Figure
5.19.
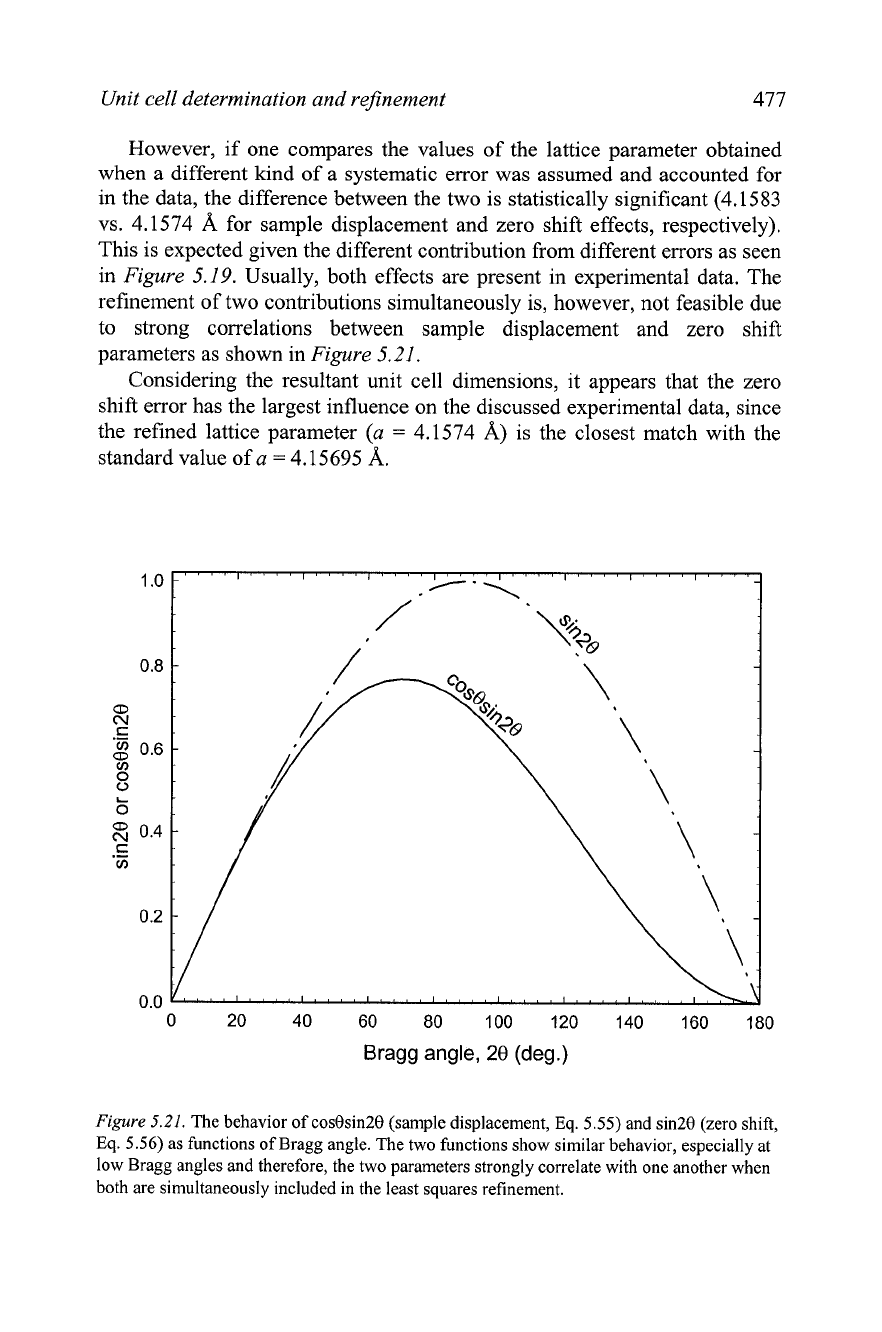
Usually, both effects are present in experimental data. The
refinement of two contributions simultaneously is, however, not feasible due
to strong correlations between sample displacement and zero shift
parameters as shown in Figure
5.21.
Considering the resultant unit cell dimensions, it appears that the zero
shift error has the largest influence on the discussed experimental data, since
the refined lattice parameter (a
=
4.1574 A) is the closest match with the
standard value of a
=
4.15695
A.
0 20 40 60 80 100 120 140 160 180
Bragg angle,
28
(deg.)
Figure
5.21.
The behavior of cos0sin20 (sample displacement, Eq.
5.55)
and sin28 (zero shift,
Eq.
5.56)
as functions of Bragg angle. The two functions show similar behavior, especially at
low Bragg angles and therefore, the two parameters strongly correlate with one another when
both are simultaneously included in the least squares refinement.

478
Chapter
5
Lattice parameters, determined by any of the three indexing programs
considered in this chapter, are usually refined using the least squares method.
On one hand, their accuracy is quite satisfactory if the unit cell dimensions
will be employed in database searches or in full pattern decomposition by
using either Le Bail or
Pawley technique (Chapter
6),
or in Rietveld
refinement (Chapter 7). Both full profile approaches result in the highest
precision of lattice parameters, which can be achieved for a specific dataset.
On the other hand, lattice parameters refined during the indexing are
imprecise because of missed or improperly handled systematic errors.
Furthermore, only a limited subset of Bragg reflections, usually at low
angles, and therefore, most affected by various systematic errors, is
employed during
ab initio
indexing. When precise unit cell dimensions are
required, their accuracy after automatic indexing can be improved by
including additional Bragg reflections into the least squares procedure
without involving full profile methods. The entire pattern should be indexed
as described in section 5.4, and all resolved Bragg peaks should be included
in the least squares minimization.
Considering the pattern of
(CH3NH3)2M07022, which is shown in
Figure
5.15, its complexity is due to the relatively large unit cell and monoclinic
symmetry coupled with a typical resolution of a conventional laboratory
diffractometer. As a result, a substantial Bragg peak overlap is observed,
especially at high angles. The first 30 resolved peaks below 28
=
30" were
indexed as shown in section 5.12.2. The remaining 57 resolvable Bragg
peaks between
30
and
51"
28
were indexed manually, using a solution with
the highest figure of merit from
Table
5.22.
A
least squares refinement
employing all 87 Bragg peaks resulted in the following lattice parameters:
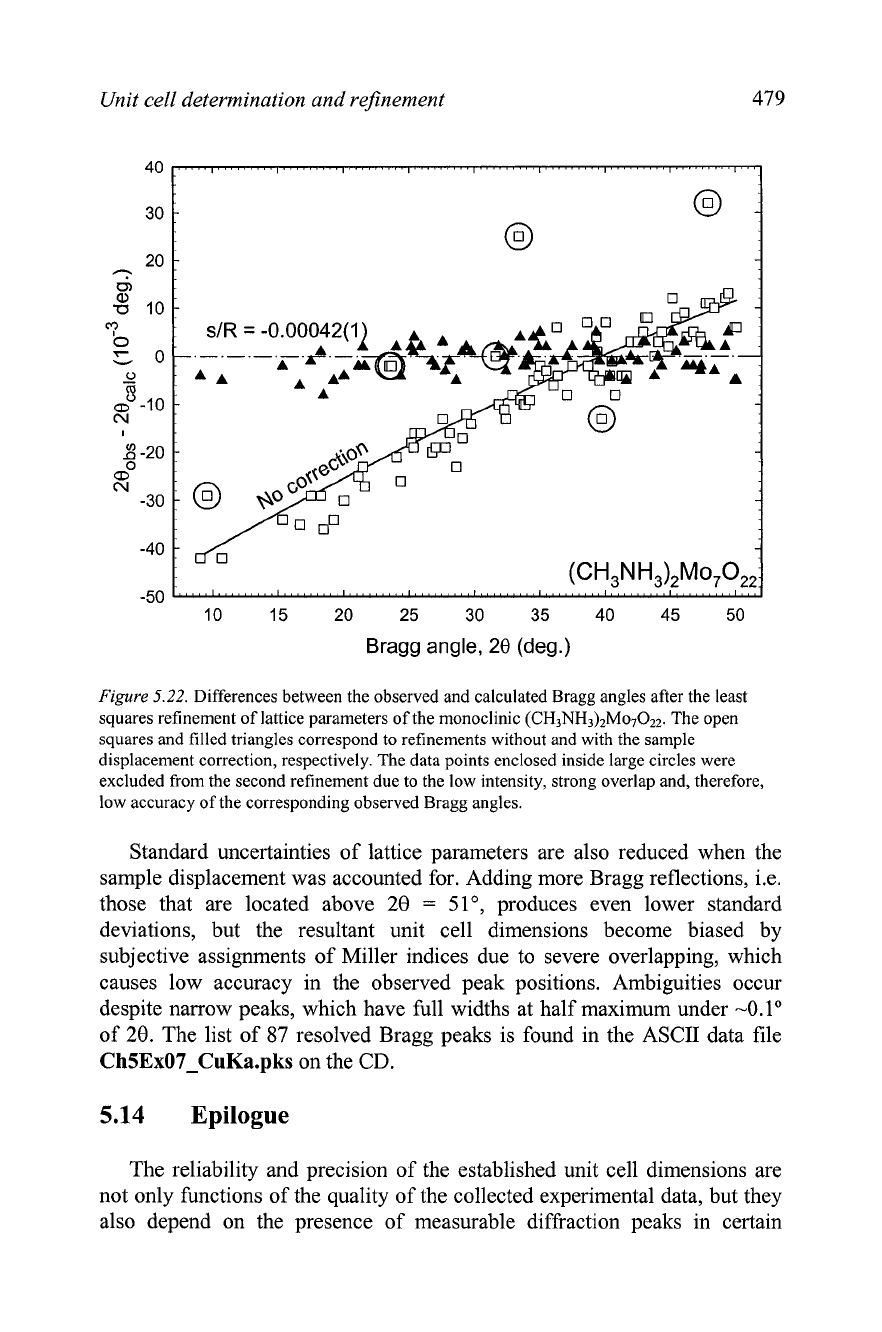
The differences between the observed and calculated Bragg angles are
shown in
Figure
5.22 as open squares. They clearly indicate the presence of
a systematic error. Furthermore, several differences are far away from the
gradually varying 2eOb,
-
28,,,, behavior. These peaks are marked with large
circles in the figure, and all of them are weak andlor are heavily overlapped
with strong neighboring Bragg reflections. A second least squares
refinement of the lattice parameters together with sample displacement
optimization after excluding the five marked reflections produces
and sample displacement parameter,
SIR
=
-0.00042(1). Much lower
discrepancies between the observed and calculated 28 are noteworthy.
Unit cell determination and rejhement
479
Bragg angle,
28
(deg.)
Figure
5.22.
Differences between the observed and calculated Bragg angles after the least
squares refinement of lattice parameters of the monoclinic (CH3NH3)2M07022 The open
squares and filled triangles correspond to refinements without and with the sample
displacement correction, respectively. The data points enclosed inside large circles were
excluded from the second refinement due to the low intensity, strong overlap and, therefore,
low accuracy of the corresponding observed Bragg angles.
Standard uncertainties of lattice parameters are also reduced when the
sample displacement was accounted for. Adding more Bragg reflections, i.e.
those that are located above
28
=
51•‹, produces even lower standard
deviations, but the resultant unit cell dimensions become biased by
subjective assignments of Miller indices due to severe overlapping, which
causes low accuracy in the observed peak positions. Ambiguities occur
despite narrow peaks, which have full widths at half maximum under
-0.1"
of
29.
The list of
87
resolved Bragg peaks is found in the ASCII data file
ChSEx07-CuKa.pks
on the CD.
5.14
Epilogue
The reliability and precision of the established unit cell dimensions are
not only functions of the quality of the collected experimental data, but they
also depend on the presence of measurable diffraction peaks in certain
480
Chapter
5
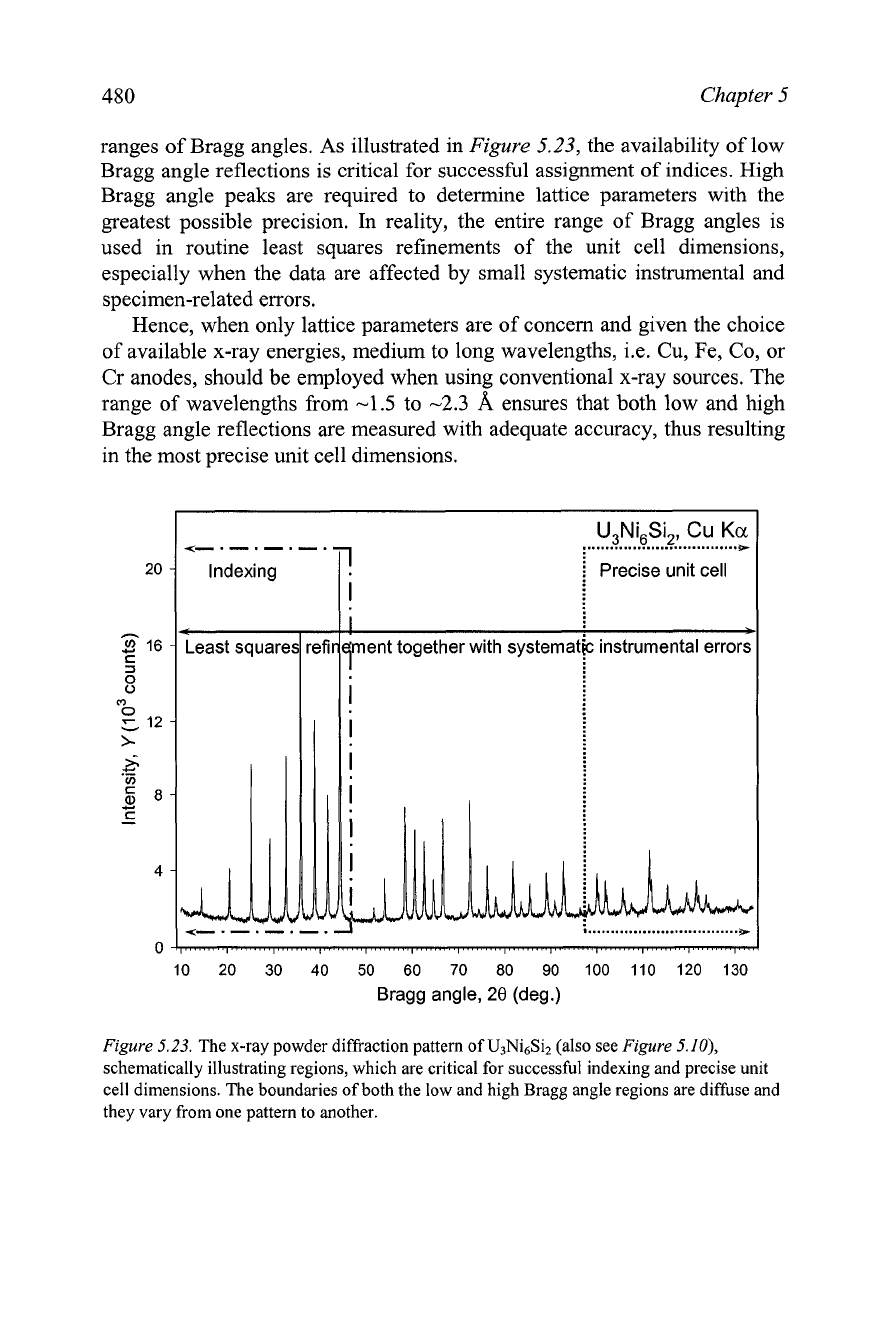
ranges of Bragg angles. As illustrated in
Figure
5.23,
the availability of low
Bragg angle reflections is critical for successful assignment of indices. High
Bragg angle peaks are required to determine lattice parameters with the
greatest possible precision.
In
reality, the entire range of Bragg angles is
used in routine least squares refinements of the unit cell dimensions,
especially when the data are affected by small systematic instrumental and
specimen-related errors.
Hence, when only lattice parameters are of concern and given the choice
of available x-ray energies, medium to long wavelengths,
i.e. Cu, Fe, Co, or
Cr anodes, should be employed when using conventional x-ray sources. The
range of wavelengths from
-1.5
to
-2.3
1$
ensures that both low and high
Bragg angle reflections are measured with adequate accuracy, thus resulting
in the most precise unit cell dimensions.
<-.-.-.-.
U Ni
Si
,
Cu
Ka
....
..............
1
:.....
3
6
....?
*
Indexing
i
Precise unit cell
I
!
least squares refi ment together with systemat& instrumental error;
'i
I
I
.................................
p
10 20 30 40 50 60 70 80 90 100 110 120 130
Bragg angle,
29
(deg.)
Figure
5.23.
The x-ray powder diffraction pattern of U3Ni6Si2 (also see
Figure
5.
lo),
schematically illustrating regions, which are critical for successful indexing and precise unit
cell dimensions. The boundaries of both the low and high Bragg angle regions are diffuse and
they vary from one pattern to another.

Unit cell determination and rejnement
48
1
5.15
Additional reading
1.
P.-E. Werner, Autoindexing, in:
:
Structure determination from powder
diffraction data. IUCr monographs on crystallography
13.
W.
I.
F.
David,
K.
Shankland, L.B. McCusker, and Ch. Baerlocher, Eds., Oxford
University Press, Oxford, New York (2002).
2.
H.
Lipson and
H.
Steeple, Interpretation of x-ray powder diffraction
patterns, MacMillan, London (1 970).
3. P.-E. Werner, L. Eriksson and M. Westdahl, A semi-exhaustive trial-and-
error powder indexing program for all symmetries,
J.
Appl. Cryst.
18,
367 (1985).
4.
A. Boutlif and D. Louer, Indexing of powder diffraction patterns for low
symmetry lattices by the successive dichotomy method, J. Appl. Cryst.
24,987 (1991).
5.
J.W. Visser, A fully automatic program for finding the unit cell from
powder data, J. Appl. Cryst.
2,
89 (1969).
6.
E.
Prince and P.T. Boggs, Least squares, in: International Tables for
Crystallography, Vol. C, Second edition, Kluwer Academic Publishers,
Boston/Dordrecht/London,
p.672 (1999) and references therein.
