Пчельник В.К. Пособие по курсу высшая математика. Матрицы и определители

Министерство образования Республики Беларусь

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

«ГРОДНЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИМЕНИ ЯНКИ КУПАЛЫ»

ИНСТИТУТ ПОСЛЕДИПЛОМНОГО ОБРАЗОВАНИЯ

ГрГУ ИМ. Я.КУПАЛЫ

МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ

Пособие по курсу

«Высшая математика»

для студентов технических специальностей

Гродно 2007

УДК 681.3(076)

ББК 32.973

Рецензенты

: кандидат физико-математических наук, доцент

А.А.Денисковец;

кандидат физико-математических наук, доцент

кафедры дифференциальных уравнений и

оптимального управления ГрГУ им.

Я.Купалы З.М.Наркун.

Рекомендовано советом Института последипломного образования

ГрГУ им. Я.Купалы

.

Пчельник В.К.

Матрицы и определители. Аналитическая геометрия

н

а плоскости и в пространстве: пособие

/

В.К.Пчельник,

Е

.А.Сетько, И.Н.Ревчук. – Гродно: ГрГУ, 2007. ― 164 с.

Пособие содержит краткие теоретические сведения по матричной алгебре,

аналитической геометрии на плоскости и в пространстве, примеры решения задач,

задачи для самостоятельного решения и задания для контрольной работы. В при-

ложениях приведены примеры решения задач матричной алгебры, способы по-

строение кривых на плоскости и в пространстве средствами электронных таблиц

Microsoft Excel.

УДК 681.3(076)

ББК 32.973

ISBN 985–417–692–4

©

Пчельник В.К., Сетько Е.А., Ревчук И.Н.,

2007

3 4

1. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ

Определение. Матрицей называется система m×n чисел,

расположенных в прямоугольной таблице из m строк и n

столбцов.

Числа этой таблицы называются элементами матрицы.

Для матриц используют следующие обозначения:

⎟

⎠

⎞

⎜

⎝

⎛

⎥

⎦

⎤

⎢

⎣

⎡

mnmm

n

mnmm

n

mnmm

n

aaa

...

......

...

,

...

......

...

,

...

......

...

21

22221

11211

21

22221

11211

21

22221

11211

.

Элементы a

i1

, a

i2

, ... , a

in

составляют i-ю строку (i=1, 2, ...,

m) матрицы, элементы a

1k

, a

2k

, ... , a

mk

- ее k-й столбец (k=1, 2,

..., n); a

ik

― элемент, принадлежащий i-й строке и k-му столбцу

матрицы; числа i, k называются индексами элемента a

ik

.

Матрицу, имеющую m строк и n столбцов, называют мат-

рицей размерности m×n (читается m на n). Используют и более

краткие обозначения матрицы размерности m

×

n: [a

ik

]

m,n

,||

a

ik

||

m,n

, (a

ik

)

m,n

. Матрицу обозначают также одной заглавной

буквой: А=|| a

ik

||

m,n

, В=(b

ik

)

m,n

. Если необходимо отметить, что

матрица А имеет m строк и n столбцов, то пишут А=А

m,n

или

А=А

mn

.

Определение. Две матрицы А=[a

ik

]

m,n

и В=[b

pq

]

p,q

назы-

ваются равными, если p=m, q=n и a

ik

= b

ik

(i=1, 2, ..., m; k=1, 2,

..., n) (то есть, если они имеют одинаковые размеры и их соот-

ветствующие элементы равны).

Пусть А=А

mn

. Если m=1, то матрица А называется

строчной матрицей, или матрицей-строкой. Если n=1, то

матрица А называется столбцевой матрицей или матрицей-

столбцом.

Пусть дана матрица А=А

mn

. Если m=n, то матрица А на-

зывается квадратной.

Порядком квадратной матрицы называется число ее

строк (столбцов).

Матрица, все элементы которой равны нулю, называется

нулевой.

Определение. Пусть А=(a

ik

)

m

,

n

, В=(b

ik

)

m,n

. Суммой двух

матриц называется такая матрица С=(с

ik

)

m,n

, что с

ik

= a

ik

+ b

ik

(i=1, 2, ..., m; k=1, 2, ..., n). Разностью двух матриц А и В

называется такая матрица D= (d

ik

)

m,n

, что d

ik

= a

ik

- b

ik

(i=1, 2, ..., m; k=1, 2, ..., n).

Определение. Пусть А=|| a

ik

||

m,n

,

α

― действительное чис-

ло. Тогда

α

А=А

α

=|| b

ik

||

m,n

= ||

α

a

ik

||

m,n

.

Определение. Произведением матрицы А

mn

= || a

ik

||

m,n

на

матрицу В

nl

= ||b

ik

||

n,l

называется такая матрица С

ml

=||c

ik

||

m,l

,

для которой

∑

=

=+++=

n

j

jkijnkinkikiik

babababac

1

2211

...

т.е., элемент

с

ik

матрицы С

ml

равен сумме произведений эле-

ментов

i-й строки матрицы А

mn

на соответствующие элементы

k-го столбца матрицы В

nl

.

Определение.

Если АВ=ВА, то матрицы А и В называются

перестановочными (коммутативными).

Определение. Определителем квадратной матрицы второго

порядка

⎟

⎠

⎞

⎜

⎝

⎛

=

2221

1211

aa

A

называется число, равное

|A|=a

11

a

22

- a

12

a

21

.

 Определитель матрицы называют также детерминан-

том. Для определителя матрицы

А используют сле-

дующие обозначения:

|A|,

Δ

A, det A.

Определение. Определителем квадратной матрицы

третьего порядка

5 6

⎥

⎦

⎤

⎢

⎣

⎡

=

333231

232221

131211

aaa

A

называют число

== ||

333231

232221

131211

aaa

aaа

A

.

233211332112312213

133221312312332211

aaaaaaaaa

−−−

−

+

Каждое слагаемое алгебраической суммы в правой части

последней формулы представляет собой произведение элемен-

тов матрицы, взятых по одному и только по одному из каждо-

го столбца и каждой строки.

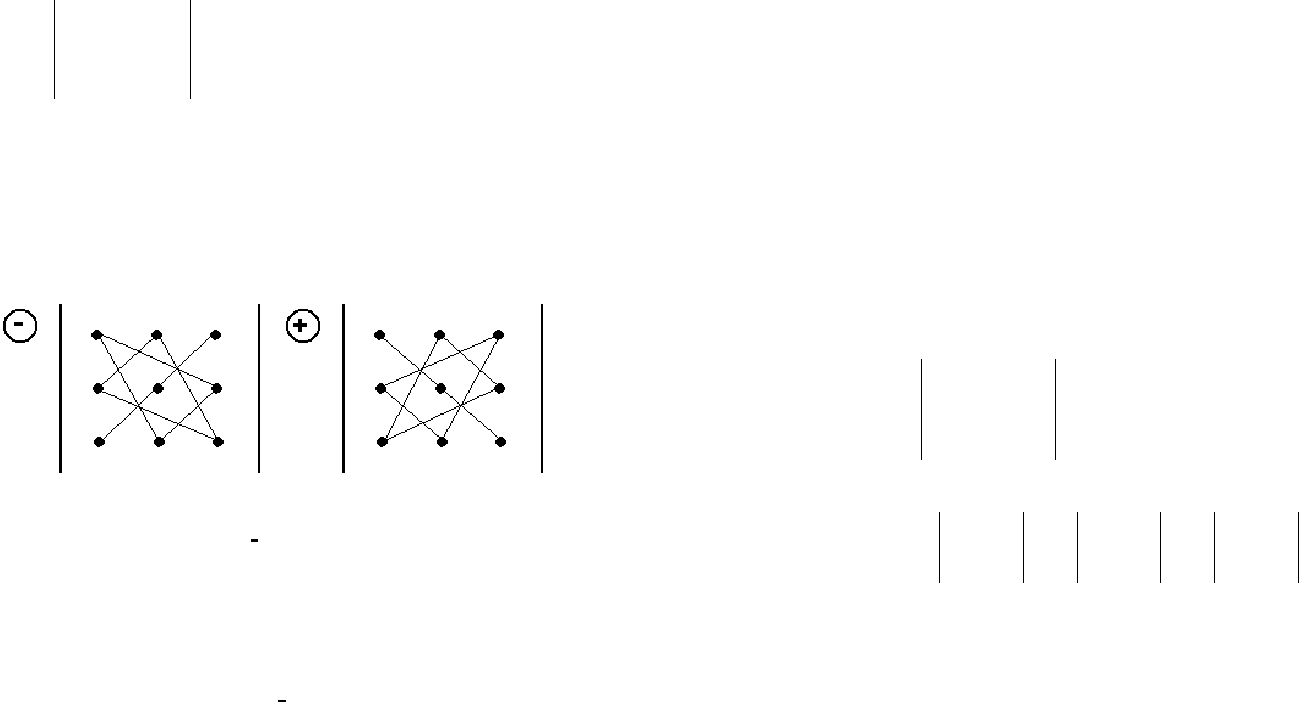
Для определения знака произведения полезно знать пра-

вило, схематически изображенное на рис.1.

Рисунок 1

Определение. Минором М

ij

элемента а

ij

определителя на-

зывается определитель, полученный из исходного вычеркива-

нием

i-й строки и j-го столбца.

Определение. Алгебраическим дополнением А

ij

элемента

а

ij

определителя называют число А

ij

=(-1)

i+j

М

ij

, где М

ij

― ми-

нор элемента

а

ij

.

Свойства определителей:

1. определитель не изменяется при замене всех строк соот-

ветствующими столбцами;

2. при перестановке двух строк (столбцов) определитель лишь

меняет знак;

3. определитель с двумя одинаковыми строками (столбцами)

равен нулю;

4. общий для всех элементов строки (столбца) множитель

можно вынести за знак определителя;

5. определитель не изменится, если к элементам

некоторой

строки (столбца) прибавить соответствующие элементы другой

строки (столбца);

6. определитель не изменится, если все элементы некоторой

строки (столбца) умножить на одно и то же число, отличное от

нуля;

7. если все элементы некоторой строки (столбца) определите-

ля равны нулю, то он равен нулю;

8. определитель равен сумме произведений элементов любой

строки (столбца) на их алгебраические дополнения.

Свойство 8 для матриц третьего порядка можно выразить

формулой:

.

aa

a

aa

a

aa

a

aaa

aaа

3231

2221

13

3331

2321

12

3332

2322

11

131312121111

333231

232221

131211

+−=

=++= AAA

Эта формула представляет собой разложение определи-

теля третьего порядка по первой строке.

Свойство 7 содержит в себе способ вычисления опреде-

лителей четвертого порядка и выше. Согласно свойству 5 мож-

7 8

но преобразовать матрицу к «треугольному» виду (в этом слу-

чае определитель равен произведению диагональных элемен-

тов) либо так, чтобы все элементы некоторой строки (столбца),

кроме, быть может, одного, равнялись нулю (в этом случае,

разлагая определитель по элементам выбранного ряда, можно

понизить порядок определителя).

Определение. Квадратная матрица А

-1

называется обрат-

ной квадратной матрице

А, если выполняется условие:

А

-1

А=АА

-1

=Е, где Е ― единичная матрица, то есть, матрица

вида

.

1...000

.......

0...100

0...010

0...001

⎟

⎠

⎞

⎜

⎝

⎛

=E

Определение. Если |A|

≠

0, то квадратная матрица А назы-

вается невырожденной (неособенной).

Если

|A|

≠

0, то матрица

А=

⎥

⎦

⎤

⎢

⎣

⎡

nnnn

n

aaa

...

......

...

21

22221

11211

имеет обратную матрицу, которая определяется по формуле

,

...

......

...

||

1

21

22212

12111

1

nnnn

n

AAA

A

A =

−

где

А

ik

― алгебраическое дополнение элемента а

ik

матрицы А.

Определение. Рангом матрицы называется наивысший из по-

рядков ее миноров, отличных от нуля.

1.1. Примеры решения типовых задач

Пример 1. Найти сумму двух матриц

.

864

751

13-18-

=B ,

1283

123

857

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

−−

=A

Решение. По определению

=

⎟

⎠

⎞

⎜

⎝

⎛

+

⎟

⎠

⎞

⎜

⎝

⎛

−−

=+

864

751

13-18-

1283

123

857

BA

.

4141

874

561

8126843

715213

1381587

⎟

⎠

⎞

⎜

⎝

⎛

−

−−

=

⎟

⎠

⎞

⎜

⎝

⎛

+−++−

+++

−+−

=

Ответ:

⎟

⎠

⎞

⎜

⎝

⎛

−

−−

4141

874

561

.

9 10

Пример 2. Даны матрицы

.

13

5-2-

=B ,

53

21

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

−

=A

Найти матрицу Х, удовлетворяющую условию 3А-2Х=5В.

Решение. Имеем:

.

2

53

,523

BA

XBXA

−

==− Умножая

А и В на числа 3 и 5 соответственно и пользуясь определением

разности двух матриц, получим:

.

53

5,155,3

106

317

2

1

515159

256103

2

1

515

2510

159

63

2

1

⎥

⎦

⎤

⎢

⎣

⎡

−

=

⎥

⎦

⎤

⎢

⎣

⎡

−

=

⎥

⎦

⎤

⎢

⎣

⎡

−−

++−

=

⎟

⎠

⎞

⎜

⎝

⎛

⎥

⎦

⎤

⎢

⎣

⎡

−−

−

⎥

⎦

⎤

⎢

⎣

⎡

−

=X

Ответ:

35 155

35

,,

−

⎡

⎣

⎢

⎤

⎦

⎥

.

Пример 3. Найти произведение матриц АВ и ВА, если

.

123

345

432

=B ,

123

642

751

⎟

⎠

⎞

⎜

⎝

⎛

−−−

⎟

⎠

⎞

⎜

⎝

⎛

−−−

=A

Решение. По определению

1)1()3()2(432)1()4()2(333)1()5()2(23

16)3(44226)4(43236)5(422

17)3(54127)4(53137)5(521

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅−+−⋅

−+⋅−⋅−+−⋅−+⋅−⋅−+−⋅−+⋅−

⋅+−⋅+⋅⋅+−⋅+⋅⋅+−⋅+⋅

=⋅BA

,

731

222

432

⎟

⎠

⎞

⎜

⎝

⎛

−−

−−−

=

.

32214

56354

28144

)1(16273)2(14253)3(12213

)1()3(6)4(75)2()3(4)4(55)3()3(2)4(15

)1(46372)2(44352)3(42312

⎟

⎠

⎞

⎜

⎝

⎛

−−−

−

=

⎟

⎠

⎞

⎜

⎝

⎛

−⋅+⋅+⋅−⋅+⋅+⋅−⋅+⋅+⋅

−⋅−+⋅−+⋅−−⋅−+⋅−+⋅−−⋅−+⋅−+⋅−

−⋅+⋅+⋅−⋅+⋅+⋅−⋅+⋅+⋅

=⋅AB

Ответ:

,

731

222

432

⎟

⎠

⎞

⎜

⎝

⎛

−−

−−−

=AB

⎟

⎠

⎞

⎜

⎝

⎛

−−−

−

=

32214

56354

28144

BA

.

Пример 4. Дана матрица

.

724

511

032

⎥

⎦

⎤

⎢

⎣

⎡

−

=A

Найти алгеб-

раические дополнения элементов второго столбца.

Решение.

.10

51

02-

)1(

,14

74

02

)1(A ,13

74

51

)1(

32

23

22

21

12

=−=

−

−==−=

+

++

AA

Ответ: А

12

=13; А

22

=-14; А

23

=10.

11 12

Пример 5. Вычислить определитель:

.

724

511

032

−

=Δ

Решение. Раскладывая определитель по первой строке,

получим:

.7339340)207(3)107(2

24

11

0

74

51

)1(3

72

51

)2(

=+=+−⋅−−−⋅−=

=

−

⋅+⋅−⋅+

−

⋅−=Δ

Ответ: Δ=73.

Пример 6. Вычислить определитель четвертого порядка

,

8242

5321

3651

5121

−

−−

−

Решение.

Способ 1. Приведем определитель к треугольному виду. Для

этого из второй строки вычтем первую, к третьей строке при-

бавим первую, к четвертой строке прибавим первую, умно-

женную на (-2). Получим:

.12)2(231

2000

10200

2730

5121

8242

5321

3651

5121

−=−⋅⋅⋅=

−

=

−

−−

−

=

A

Способ 2. Сначала вынесем общий множитель четвертой стро-

ки за знак определителя, а затем преобразуем матрицу так, что-

бы в четвертой строке остался один ненулевой элемент:

.12)3428(2)17247(2

42

177

)1()1(2

1742

27177

100

2

1742

27177

100

)1()1(2

0100

17342

276177

1100

4121

5321

3651

5121

2

8242

5321

3651

5121

31

34

−=−⋅=⋅−⋅⋅=−⋅−⋅

=⋅=−⋅−⋅=

=

−

=

−

−−

−

⋅=

−

−−

−

=

+

A

Для этого сложим первый и третий столбцы, ко второму столб-

цу прибавим третий, умноженный на 2, а к четвертому столбцу

прибавим третий, умноженный на четыре. Полученный опре-

делитель разложим согласно свойству 7 по элементам четвер-

той строки. Полученный в качестве минора определитель

третьего порядка вновь можно разложить по элементам первой

строки.

Пример 7.

Выяснить, существует ли матрица, обратная

матрице

,

131

200

101

⎥

⎦

⎤

⎢

⎣

⎡

−

=A

и если существует, то найти ее.

Решение. Так как detA=-6

≠

0, то матрица А невырожден-

ная, и А

-1

существует.

Способ 1. Находим алгебраические дополнения элементов мат-

рицы А:

,6 ,0

31

00

,2

11

20

,6

13

20

11131211

−==

−

=−=

−

−=−== AAAA

13 14

.0

00

01

,2

20

11

,0

20

10

,3

31

01

,2

11

,3

13

10

333231

232221

==−=−===

−=

−

−==

−

==−=

AAA

Следовательно,

.

030

222

036

6

1

⎥

⎦

⎤

⎢

⎣

⎡

−

−−

−

−=

−

A

Способ 2. Найдем А

-1

с помощью элементарных преобразова-

ний над строками матрицы С:

.

100

010

001

131

200

101

−

→C

Прибавив к третьей строке первую, получим:

.

101

010

001

230

200

101

→C

Поменяем местами вторую и третью строки. Тогда

.

001

101

001

200

230

101

→C

Прибавив ко второй строке третью, умноженную на (-1), полу-

чим:

.

010

111

001

200

030

101

−→C

Умножив вторую строку на 1/3, а третью ― на 1/2, имеем:

.

0

2

1

0

3

1

3

1

3

1

001

100

010

101

−→C

Вычтем из первой строки третью. Тогда

=

⎥

⎦

⎤

⎢

⎣

⎡

−

=−

−

→

0

2

1

0

3

1

3

1

3

1

0

2

1

A ,

0

2

1

0

3

1

3

1

3

1

0

2

1

100

010

001

1-

C

.

030

222

036

6

1

⎥

⎦

⎤

⎢

⎣

⎡

−

−−

−

−=

Пример 8. Найти Х из матричного уравнения АХ=В, где

А – квадратная матрица порядка 3, Х и В – матрицы, содержа-

щие по одному столбцу и по 3 строки:

.

5

1

4

,

131

200

101

⎟

⎠

⎞

⎜

⎝

⎛

−=

⎟

⎠

⎞

⎜

⎝

⎛

−

= ВA

15 16

Решение. Домножив левую и правую части уравнения

АХ=В слева на матрицу, обратную матрице А, получим:

.

1111

ВАХВАЕХВААХА

−−−−

=→=→=

Найдем матрицу

1−

А (см. пример 7):

.

030

222

036

6

1

⎟

⎠

⎞

⎜

⎝

⎛

−

−−

−

−=

−

А

Перемножая найденную обратную матрицу на матрицу В, по-

лучим:

.

3

20

27

6

1

⎟

⎠

⎞

⎜

⎝

⎛

−

−=Х

Примечание. Примеры использования формул для

решения задач матричной алгебры средствами электронных

таблиц Microsoft Excel приведены в приложении 1.

1.2. Задачи для самостоятельного решения

1. Найти сумму и разность двух матриц:

;

1711

53

=B ,

138

72

1)

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

=A ,

1258

983

721

2)

⎟

⎠

⎞

⎜

⎝

⎛

−

−−=A

.

1272

385

321

=B ,

425

5118

357

3);

642

8119

1372

=B

⎟

⎠

⎞

⎜

⎝

⎛

−

−−−

⎟

⎠

⎞

⎜

⎝

⎛

−=

⎟

⎠

⎞

⎜

⎝

⎛

− A

2. Даны три матрицы

.

67

45

23

C ,

71

64

32

B ,

86

73

51

⎥

⎦

⎤

⎢

⎣

⎡

−

−=

⎥

⎦

⎤

⎢

⎣

⎡

−

=

⎥

⎦

⎤

⎢

⎣

⎡

−

=A

Найти:

1)

А + В + С; 2) А - В - С; 3) 3А - 2В + С; 4) 2А + 4В - 3С.

3. Дана матрица

.

524

834

621

⎥

⎦

⎤

⎢

⎣

⎡

−

=A

Найти матрицу Х, удовле-

творяющую условию

3А + 2Х = Е.

4. Даны матрицы .

31

25

B ,

35

12

⎥

⎦

⎤

⎢

⎣

⎡

−−

=

⎥

⎦

⎤

⎢

⎣

⎡

−

=A

Найти матрицу

Х, удовлетворяющую условию 2А - 3Х = В.

5.

Найти произведения матриц:

[][]

;

1-

4

3

541 3) ;762

2

1-

3

2) ;

61-

50

21-

13

)1

⎥

⎦

⎤

⎢

⎣

⎡

⋅−−⋅

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⋅

⎥

⎦

⎤

⎢

⎣

⎡

;

100

020

005

401-

725

642

)5 ;

04

01

10

21

3215

0432-

)4

⎥

⎦

⎤

⎢

⎣

⎡

−

⋅

⎥

⎦

⎤

⎢

⎣

⎡

−

⎥

⎦

⎤

⎢

⎣

⎡

−

⋅

⎥

⎦

⎤

⎢

⎣

⎡

−

;

100

050

003

800

010

002

)7 ;

300

030

003

32-1

054

123

)6

⎥

⎦

⎤

⎢

⎣

⎡

−

⋅

⎥

⎦

⎤

⎢

⎣

⎡

−

⎥

⎦

⎤

⎢

⎣

⎡

⋅

⎥

⎦

⎤

⎢

⎣

⎡

−

17 18

.

03

12

11

20

12

210

31-2

)9 ;

5

3

15

32

03

1-2

8)

⎥

⎦

⎤

⎢

⎣

⎡

−

⋅

⎥

⎦

⎤

⎢

⎣

⎡

−

⋅

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⋅

⎥

⎦

⎤

⎢

⎣

⎡

⋅

⎥

⎦

⎤

⎢

⎣

⎡

6.

Даны матрицы .

43

2-5

41

3-2

=B ,

2311

0032

3401

5321

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

−

−−

=A

Найти

элемент

с

42

матрицы С=АВ.

7.

Проверить, имеет ли место равенство

()

,2

22

BABABA ++=+ если

.

30

1-2

=B ,

03-

21

=A 2) ;

3-0

03-

=B ,

42

51

=A )1

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

8.

Вычислить указанные определители:

.

13-2-

053

21-1

6) ;

01-1

42-3

1-32

)5

211

3-01

231-

4) ;

34-2

513

21-2

3) ;

35

01-

2) ;

43

1-2

)1

9. Вычислить указанные определители, пользуясь их свойства-

ми:

;

4171-13

9907

1521

421-3

3) ;

7531

1357

2419144

4838288

2) ;

1391327

0000

91187153

18-72

)1

34542790

34532789

6) ;

3-3-3-

126252377

127253378

5) ;

15-83

6-10

1-21

)4

;

321

432

543

8) ;

317217

181181

)7

.

10. При каких значениях

α

ранг матрицы

⎥

⎦

⎤

⎢

⎣

⎡

−

64

021

312

α

равен 2?

11.

При каком значении

α

ранг матрицы

⎥

⎦

⎤

⎢

⎣

⎡

−

321

241682

1312

12841

α

равен

3?

12.

Найти матрицы, обратные данным, если они существуют:

;

321-

504

32-1

4) ;

600

050

001

3) ;

71

83

2) ;

53-

112

)1

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

.

2-11

33-1

5-21

6) ;

1022-

653-

43-1

5)

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

19 20

2. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ И МЕТОДЫ

ИХ РЕШЕНИЯ

Системой линейных алгебраических уравнений, содер-

жащей m уравнений и n неизвестных, называется система вида

⎪

⎩

⎪

⎨

⎧

=+++

,...

........................................

,...

2211

22222121

11212111

mnmnmm

nn

bxaxaxa

(1)

где

njmia

ij

,1 ,,1 , == называются коэффициентами системы, а

числа

i

b — свободными членами. Матрица

(

)

,

ij

aA

=

состав-

ленная из коэффициентов системы, называется матрицей сис-

темы. Расширенной матрицей называется матрица

В, получен-

ная из

А дополнением столбцом свободных членов.

Решением системы (1) называется совокупность n дейст-

вительных чисел

(

)

n

α

,...,,

21

, при подстановке которых вме-

сто неизвестных все уравнения системы обращаются в верные

равенства.

Система (1) называется совместной, если она имеет хотя

бы одно решение, и несовместной, если она не имеет решений.

Если

,0 det

≠

A то система (1) называется невырожден-

ной.

Невырожденная система n линейных уравнений с n не-

известными имеет единственное решение, которое может быть

найдено по формуле Крамера:

, ,1 , nix

i

=

Δ

=

где

, det A=Δ определитель

i

Δ получается из Δ заменой i-го

столбца столбцом свободных членов.

Система линейных алгебраических уравнений (ЛАУ)

может быть записана в матричном виде

Ах=b, где А — матри-

ца системы,

(

)

(

)

. ..., , , , ..., , ,

2121 n

T

n

bbbbxxxx == Невырожден-

ная система n линейных уравнений с n неизвестными может

быть решена матричным способом, то есть решение может

быть получено по формуле

,

1

bAx

−

=

где

1−

A ― матрица, обратная матрице А.

Напомним, что рангом матрицы А называется наиболь-

ший из порядков миноров данной матрицы, отличных от нуля.

Обозначается ранг матрицы

r, r(A) или rang A. Минор, порядок

которого определяет ранг матрицы, называется базисным. У

матрицы может быть несколько базисных миноров.

Элементарными преобразованиями матрицы называются:

1)

умножение любого ряда матрицы на число, отличное от

нуля;

2)

прибавление к одному ряду матрицы другого параллель-

ного ряда, умноженного на любое число;

3)

перестановка двух параллельных рядов матрицы.

Свойства ранга матрицы:

а)

ранг матрицы не меняется при транспонировании;

б)

ранг матрицы не меняется при отбрасывании нулевого

ряда;

в)

ранг матрицы не меняется при элементарных преобразо-

ваниях.

Критерий совместности Кронекера-Капелли

Для того, чтобы система (1) была совместной, необходи-

мо и достаточно, чтобы ранг матрицы системы был равен

рангу расширенной матрицы системы, то есть r(A) = r(B).

Если в системе (1)

,0...

21

=

n

bbb то такая система

называется однородной. Однородная система всегда совместна,

так как всегда имеет нулевое решение. Поэтому представляет

Пчельник В.К. Пособие по курсу высшая математика. Матрицы и определители

Подождите немного. Документ загружается.