Пчельник В.К. Пособие по курсу высшая математика. Матрицы и определители

61 62

Рисунок 11 б Рисунок 11 в

Рисунок 11 г

7.1. Примеры решения типовых задач

Пример 1. Написать уравнение окружности, касающейся

осей координат и проходящей через точку А(1; 2).

Решение. Так как окружность касается осей координат и

лежит в первой четверти, то ее радиус равен R, а центр имеет

координаты (R; R). Учитывая, что окружность проходит через

точку А(1; 2), получаем уравнение (1 - R)

2

+ (2 - R)

2

= R

2

. Пре-

образуем его: R

2

- 6·R + 5 + 0 ⇒ (R - 5) · (R - 1) = 0. Корни

полученного уравнения равны R

1

= 1, R

2

= 5.

Ответ: (х - 1)

2

+ (у - 1)

2

= 1, (х - 5)

2

+ (у - 5)

2

= 25.

Пример 2. Даны точки А(-3; 0) и В(3; 6). Написать урав-

нение окружности, диаметром которой служит отрезок АВ.

Решение. Согласно условию точка О(α;β) ― середина

отрезка АВ ― является центром искомой окружности. Поэто-

му

α = (-3 + 3)/2 = 0, β = (0 + 6)/2 = 3. Радиус R окружности ра-

вен.

23

2

26

2

3636

2

==

+

===

AB

OAR

.

Уравнение искомой окружности имеет вид:

х

2

+ (у-3)

2

= 18.

Ответ: х

2

+ (у-3)

2

= 18.

Пример 3. Написать уравнение окружности, проходящей

через точки

А(-1; 3), В(0; 2) и С(1; -1).

Решение. Найдем середину Е отрезка АВ:

2

5

2

23

;

2

1

2

01

=

+

−=

+

−

. Проведем через точку

⎟

⎠

⎞

⎜

⎝

⎛

−

2

5

;

2

1

E

прямую ЕО, перпендикулярную прямой АВ

(рис. 12):

.22

01

0

23

2

+−=⇒−=−⇒

−−

−

=

−

xyxy

xy

k

AB

= -1, k

EO

= 1. Уравнение прямой ЕО имеет вид

63 64

.

2

1

2

5

+=− xy (*)

A

E

B

F

C

O

Рисунок 12

Проведем через точку

⎟

⎠

⎞

⎜

⎝

⎛

2

1

;

2

1

F

прямую FO, перпенди-

кулярную прямой

ВС:

.23

10

1

12

1

+−=⇒

−

=

+

xy

k

BC

= -3, k

FO

= 1/3. Уравнение прямой FO имеет вид

.

3

2

1

2

1

−

=−

x

y

(**)

Решив систему уравнений (*) и (**), найдем координаты

точки О:

⎩

⎨

⎧

+=

13

,3

xy

.

Получаем О(-4; -1). Найдем радиус окружности:

()()

.53114

22

=−−++−== OAR

Уравнение окружности имеет вид (х + 4)

2

+ (у + 1)

2

= 25.

Ответ: (х + 4)

2

+ (у + 1)

2

= 25

Пример 4. Составить уравнение окружности, имеющей

центр на прямой

4х - 5у - 3 = 0 и касающейся двух прямых

2х-3у-10=0, 3х-2у+ 5 = 0.

Решение. Пусть О ― центр искомой окружности О(

α;β

).

Тогда расстояния от точки

О до прямых 2х-3у-10=0 и

3х-2у+ 5 = 0 равны:

.

13

523

94

1032 +−

=

+

−−

βαβα

С другой сто-

роны, точка

О(

α;β

) принадлежит прямой 4х - 5у - 3 = 0. Таким

образом, для определения координат точки О получаем систе-

му:

⎩

⎨

⎧

+−=−−

=−−

.

5231032

,0354

βαβα

βα

Она распадается на две системы:

I.

;5231032

,0354

⎩

⎨

⎧

+−=−−

=−−

βαβα

βα

II.

⎩

⎨

⎧

=+−+−−

=−−

.05231032

,0354

βαβα

βα

Решая их, последовательно находим:

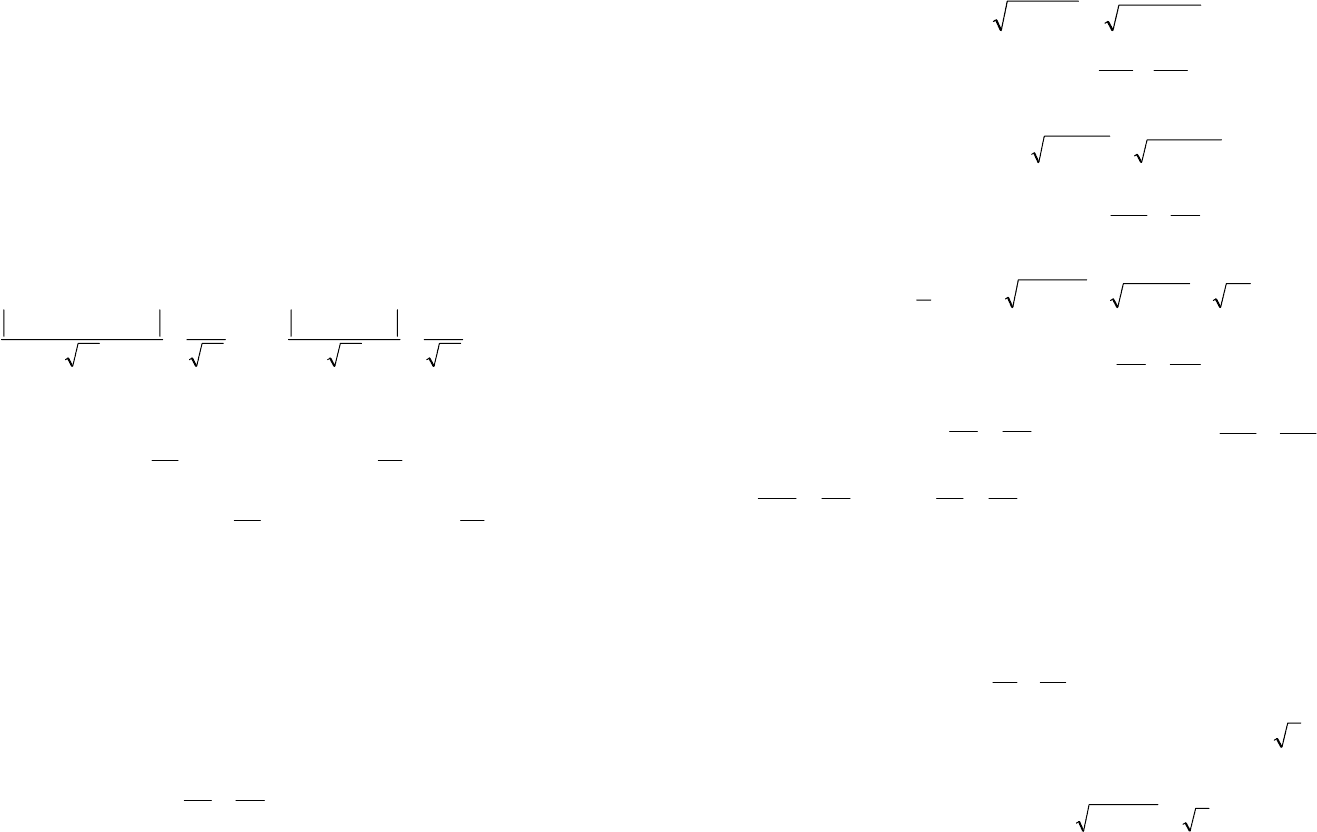
65 66

⎩

⎨

⎧

⎩

⎨

⎧

−=

⎩

⎨

⎧

=−−+

+=

⎩

⎨

⎧

=++

=+

⎩

⎨

⎧

⎩

⎨

⎧

=−−

=++

1.=

1,=

7

-8,=

;03554

,1

;015

,0729

0;=3-5-4

0,=1--

II.

;0354

,015

I.

β

α

β

α

ββ

βα

α

βα

Таким образом, получаем

О

1

(-8; -7) и О

2

(2; 1). Находим

радиусы:

.

13

9

13

10322

R ,

13

5

13

1073)8(2

21

=

−−⋅

==

−⋅+−⋅

=R

Искомые уравнения имеют вид:

()( ) ()()

.

13

81

12 ,

13

25

78

2222

=−+−=++− yxyx

Ответ:

()( ) ()()

.

13

81

12 ,

13

25

78

2222

=−+−=++− yxyx

Пример 5. Составить каноническое уравнение эллипса,

фокусы которого расположены на оси Ох симметрично отно-

сительно начала координат, если: 1) большая полуось равна

8, малая полуось равна 6; 2) расстояние между фокусами рав-

но 10, большая ось равна 26; 3) большая ось равна 20, эксцен-

триситет равен 0,6; 4) расстояние между фокусами равно 14,

эксцентриситет равен 7/9.

Решение. 1) По условию а=8, b=6. Поэтому искомое

уравнение имеет вид:

.1

3664

22

=+

yx

2) По условию

2с=10, 2а=26. Следовательно,

.1225169,5,13

22

=−=−=== cabca

Искомое уравнение имеет вид:

.1

144169

22

=+

yx

3) По условию

2а=20,

ε

=с/а=0,6. Отсюда находим:

.836100,6,10

22

=−=−=== cabca

Искомое уравнение имеет вид:

.1

64100

22

=+

yx

4) По условию 2с=14,

ε

=с/а=7/9. Отсюда находим:

.324981,9,7

22

=−=−==== cab

c

ac

ε

Искомое уравнение имеет вид:

.1

3281

22

=+

yx

Ответ: 1)

1

3664

22

=+

yx

; 2)

1

144169

22

=+

yx

;

3)

1

64100

22

=+

yx

; 4).

.1

3281

22

=+

yx

Пример 6

. Дан эллипс 9х

2

+ 5у

2

= 45. Найти: 1) его полу-

оси; 2) фокусы; 3) эксцентриситет; 4) уравнения директрис.

Решение. Преобразуем уравнение эллипса к канониче-

скому виду:

1

95

22

=+

yx

.

Его полуоси равны соответственно

3,5 == ba

(

b ― большая полуось). Находим с из условия

222

cba −= , то есть .24

22

==−= abc

Следовательно, его фокусы расположены на оси Оу и

имеют координаты

F

1

(0 ;-2), F

2

(0; 2). Находим эксцентриситет:

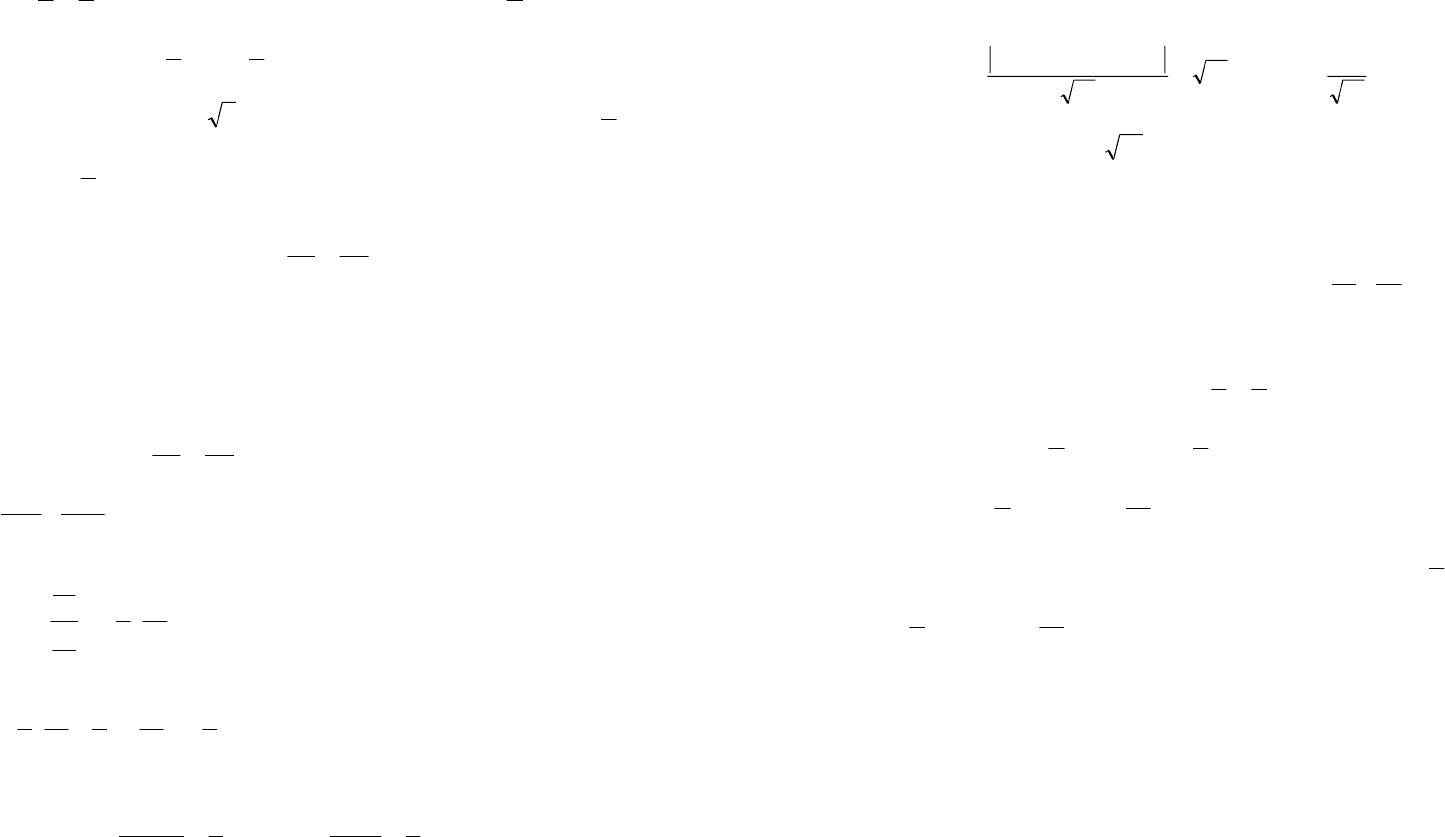
67 68

3

22

==

b

ε

. Уравнения директрис имеют вид

ε

b

y ±=

. В нашем

случае

2

9

,

3

2

,3 ±=== yb

ε

.

Ответ: 1) 3 ,5 == ba ; 2) F

1

(0; -2), F

2

(0; 2); 3)

3

2

=

ε

;

4)

2

9

±=y

.

Пример 7. На эллипсе

1

818

22

=+

yx

найти точку М

1

, бли-

жайшую к прямой

2х-3у+25=0, и вычислить расстояние d от

точки

М

1

до этой прямой.

Решение. Пусть М

1

(х

1

;у

1

) ― искомая точка. Тогда каса-

тельная в ней должна быть параллельна прямой

2х - 3у + 25= 0.

Воспользуемся следующим результатом. Уравнение касатель-

ной к эллипсу

1

2

=+

b

y

a

x

в точке М

1

(х

1

;у

1

) будет иметь вид:

.1

818

2121

=+

yyxx

Для прямой 2х - 3у + 25 = 0 угловой коэффици-

ент равен

2/3. Для касательной угловой коэффициент равен

1

y

x

9

4

18

⋅−=−=

y

x

k

. Так как прямая и касательная параллельны,

то, приравнивая их угловые коэффициенты, получим:

2

3

2

9

4

1

−=⇒=⋅−

y

x

y

x

. Так как точка М

1

(х

1

; у

1

) принадлежит

эллипсу, то с учетом последнего соотношения получаем:

2 ,1

8

1

418

9

,1

8

1

18

/

1

2

1

32

2

1

±==

⎟

⎠

⎞

⎜

⎝

⎛

+

⋅

⋅=

⎟

⎠

⎞

⎜

⎝

⎛

+⋅ yy

yx

y

.

Точки

М

1

и М

2

, удовлетворяющие полученному условию,

имеют координаты

М

1

(-3; 2) и М

2

(3; -2). Найдем расстояния от

них до прямой:

.

13

37

)( ,13

13

25)2(3)3(2

)(

21

==

+⋅−−⋅

= MdMd

Условию задачи удовлетворяет точка М

1

.

Ответ: 13 ),2 ;3( =− dM .

Пример 8. Дана гипербола 16х

2

- 9у

2

= -144. Найти: 1) по-

луоси

а и b; 2) фокусы; 3) эксцентриситет; 4) уравнения асим-

птот; 5) уравнения директрис.

Решение. Преобразуем уравнение к виду

1

169

22

−=−

yx

.

Имеем:

а=3, b=4. Находим с по формуле с

2

= а

2

+ b

2

. В нашем

случае

с=5. Фокусы гиперболы имеют координаты F

1

(0; -5),

F

2

(0;5). Находим эксцентриситет:

4

5

==

b

c

ε

. Уравнения асим-

птот имеют вид

x

a

b

y ±= или xy

3

4

±= . Уравнения директрис

имеют вид

ε

b

y ±=

или

5

16

±=y

.

Ответ: 1) а=3, b=4; 2) F

1

(0; -5), F

2

(0 ;5); 3)

4

5

=

ε

;

4)

xy

3

4

±=

; 5)

5

16

±=y

.

Пример 9

. Написать каноническое уравнение гиперболы,

фокусы которой расположены на оси

Ох симметрично относи-

тельно начала координат, если: 1)

2а=14, 2b=10; 2) расстояние

между фокусами равно

20, 2а = 12; 3) 2а=6, эксцентриситет

равен

5/3; 4) расстояние между фокусами равно 26, эксцентри-

ситет равен

2,6.

Решение. 1) По условию имеем: а=7, b=5. Тогда канони-

ческое уравнение гиперболы имеет вид:

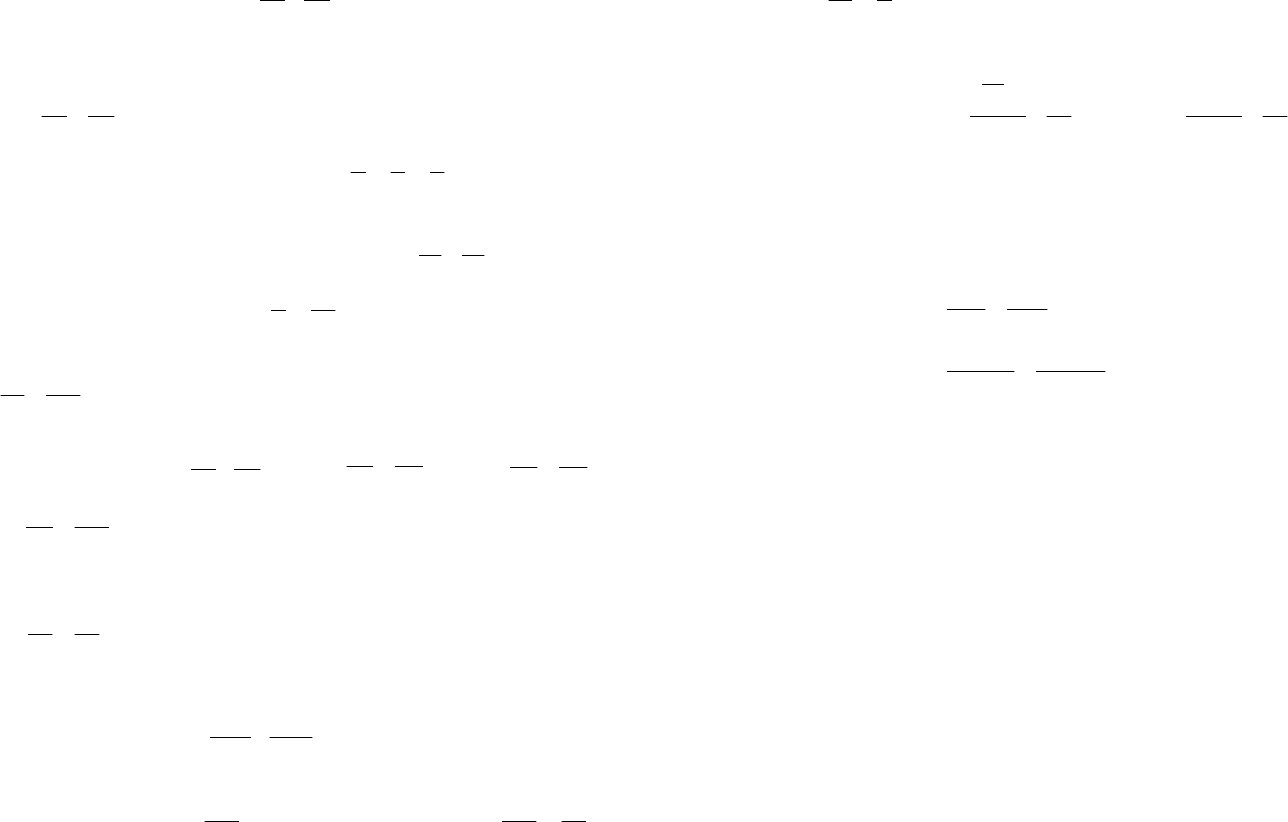
69 70

.1

2549

22

=−

yx

2) По условию

с=10, а=6. Пользуясь формулой с

2

=а

2

+ b

2

, на-

ходим

b=8. Тогда каноническое уравнение гиперболы имеет

вид

.1

6436

2

=−

y

x

3) По условию имеем

33

5

a

c

,3

c

a ====

ε

. Следовательно,

с=5. По формуле с

2

=а

2

+ b

2

находим, что b=4. Поэтому кано-

ническое уравнение гиперболы имеет вид

xy

22

916

1−=.

4) По условию

6,2

13

a

c

,13 ====

a

c

ε

. Следовательно, а=5,

b= 12.

Поэтому каноническое уравнение гиперболы имеет вид

xy

22

25 144

1−=.

Ответ

: 1)

1

2549

2

=−

y

x

; 2)

1

6436

2

=−

y

x

; 3) 1

169

2

=−

y

x

;

4)

.1

14425

22

=−

yx

Пример 10

. Составить уравнения касательных к гипербо-

ле

xy

22

16 64

1−=

, параллельных прямой 10х - 3у + 9 = 0.

Решение

. Уравнение касательной к гиперболе в точке

М

1

(х

1

; у

1

) имеет вид:

1

6416

11

=

⋅

−

⋅

yyxx

. Угловой коэффициент пря-

мой

10х - 3у + 9 = 0 равен k=10/3. Угловой коэффициент каса-

тельной равен

1

4

y

x

k =

. По условию k

1

=k и

3

104

1

=

y

x

или

6

5

1

=

y

x

. Так как точка М

1

(х

1

; у

1

) принадлежит гиперболе, то

.5,6

1

64

1

1636

25

1

64

1

16

2

1

2

1

2

1

±=±=⇒

⇒=

⎟

⎠

⎞

⎜

⎝

⎛

−

⋅

⋅⇒=

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

⋅

xy

y

x

y

Уравнения касательных имеют вид:

.0323101

64

)6(

16

)5(

;0323101

64

6

16

5

=+−⇒=

−⋅

−

−⋅

=−−⇒=

⋅

−

⋅

yx

Ответ: 10x - 3y - 32 = 0; 10x - 3y + 32 = 0.

Пример 11. Написать каноническое уравнение параболы,

если известно, что: 1) фокус находится в точке F(4; 0);

2) фокус находится в точке F(0; 3); 3) директриса имеет урав-

нение

х - 3 = 0; 4) директриса имеет уравнение у - 1= 0.

Решение. 1) Парабола симметрична относительно оси Ох;

ее каноническое уравнение имеет вид

у

2

= 2рх. Тогда ее фокус

имеет координаты

F(р/2; 0). Поэтому р/2 = 4, откуда р=8 и

у

2

= 16х.

2) Парабола симметрична относительно оси

Оу; ее канониче-

ское уравнение имеет вид

х

2

= 2qу. Тогда ее фокус имеет коор-

динаты

F(0; q/2). Следовательно, q/2 = 3, то есть, q=6,

х

2

= 12у.

3) Парабола симметрична относительно оси

Ох; ее канониче-

ское уравнение имеет вид

у

2

= 2рх. Тогда уравнение ее дирек-

трисы имеет вид

х = -р/2. Поэтому -р/2 = 3, то есть, р=-6,

у

2

= -12х.

4) Парабола симметрична относительно оси

Оу, ее канониче-

71 72

ское уравнение имеет вид х

2

= 2qу. Тогда уравнение ее дирек-

трисы

у = -q/2. Поэтому -q/2 = 2, откуда q = -4, х

2

= -8у.

Ответ: 1) у

2

= 16х; 2) х

2

= 12у; 3) у

2

= -12х; 4) х

2

= -8у.

7.2. Задачи для самостоятельного решения

1. Составить уравнение окружности в каждом из следую-

щих случаев:

1) центр окружности совпадает с началом координат и ее

радиус R=3;

2) центр окружности совпадает с точкой С(2; -3) и ее ра-

диус R=7;

3) окружность проходит через начало координат и ее

центр совпадает с точкой С(6; -8);

4) окружность проходит через точку А(2; 6) и ее центр

совпадает

с точкой С(-1; 2);

5) точки А(3;3) и В(-1; 6) являются концами одного из

диаметров окружности;

6) центр окружности совпадает с началом координат и

прямая 3х - 4у + 20 = 0;

7) является касательной к окружности;

8) центр окружности совпадает с точкой С(1; -1) и прямая

5х-12у +9 =0 является касательной к окружности;

9) окружность проходит через точки А(3; 1) и

В(-1; 3), а

ее центр лежит на прямой 3х - у - 2 = 0;

10) окружность проходит через три точки А(1; 1), В(1; -1)

и С(2; 0);

11) окружность проходит через три точки М

1

(-1; 5),

М

2

(-2; -2) и М

3

(5; 5).

2.

Точка С(3; -1) является центром окружности, отсекаю-

щей на прямой 2х -5у + 18 = 0 хорду, длина которой равна 6.

Составить уравнение этой окружности.

3.

Составить уравнение окружности, касающейся двух

параллельных прямых 2х+у - 5 = 0 и 2х + у + 15 = 0, причем

одной из них ― в точке А(2; 1).

4. Составить уравнение окружности, которая имеет центр

на прямой 2х + у = 0, касается прямых 4х - 3у + 10 = 0 и

4х - 3у - 30 = 0.

5.

Составить уравнения окружностей, проходящих через

начало координат и касающихся двух пересекающихся прямых

х + 2у - 9 = 0 , 2х - у + 2 = 0.

6.

Написать уравнения окружностей, касающихся трех

прямых: 4х-3у-10= 0, 3х - 4у - 5 = 0 и 3х - 4у- 15 = 0.

7.

Вычислить кратчайшее расстояние от точки до окруж-

ности в каждом из трех случаев:

а) А(6; -8), х

2

+ у

2

= 1; б) В(3; 9), х

2

+ у

2

- 26х + 30у + 313= 0;

в) С(-7; 7), х

2

+ у

2

- 10х - 14у - 151 = 0.

8. Составить уравнение окружности, проходящей через

начало координат и точку пересечения двух окружностей:

(х + 1)

2

+ (у + 1)

2

= 25, (х-2)

2

+(у+4)

2

= 9.

9.

Точка

) ;(

111

yxM

лежит на окружности (х-α)

2

+ (у-β)

2

=

=R

2

. Составить уравнение касательной в точке

1

M

.

10.

Составить уравнения касательных к окружностям

х

2

+ +у

2

+ 10х- 2у+6= 0, параллельных прямой 2х + у - 7 = 0.

11.

Составить уравнение эллипса, фокусы которого распо-

ложены на оси абсцисс, симметрично относительно начала

координат, зная кроме того, что:

1) его полуоси равны 5 и 2;

2) его большая полуось равна 10, а расстояние между

фокусами 2с=8;

3) его малая ось равна 24, а расстояние между фокуса-

ми 2с=10;

4) расстояние между его фокусами 2с=6 и эксцентри-

ситет

5

3

=

ε

;

5) его большая полуось равна 20, а эксцентриситет

5

3

=

ε

;

6) его малая ось равна 10, а эксцентриситет

13

12

=

ε

;

7) расстояние между его директрисами равно 5, а рас-

стояние между фокусами 2с=4;

73 74

8) его большая полуось равна 8, а расстояние между

директрисами равно 16;

9) его малая ось равна 6, а расстояние между дирек-

трисами равно 13;

10)

расстояние между его директрисами равно 32 и

2

1

=

ε

.

12.

Дан эллипс 3х

2

+ 25 у

2

= 225. Найти: 1) его полуоси;

2) фокусы; 3) эксцентриситет; 4) уравнения директрис.

13.

Вывести условие, при котором прямая у=kх+b касается

эллипса

1

2

=+

b

y

a

x

.

14.

Составить уравнение касательной к эллипсу

1

2

=+

b

y

a

x

в его точке М(х;у).

15.

Доказать, что касательные к эллипсу 1

2

=+

b

y

a

x

, про-

веденные в концах одного и того же диаметра, параллельны

(диаметром эллипса называется его хорда, проходящая через

центр).

16.

Провести касательные к эллипсу 1

2430

2

=+

y

x

парал-

лельно прямой 4х - 2у + 23 = 0 и вычислить расстояние d меж-

ду ними.

17.

Составить уравнение гиперболы, фокусы которой рас-

положены на оси абсцисс симметрично относительно начала

координат, зная, кроме того, что:

1) ее оси 2а=10, 2b=8;

2) расстояние между фокусами 2с=10, а ось 2b=8;

3) расстояние между фокусами 2с=6, а эксцентриситет

ε=3/2;

4) ось 2а=16,

ε=5/4;

5) уравнения асимптот у=

±4х/3, а расстояние между фоку-

сами 2с=20;

6) расстояние между директрисами равно

13

2

22

, а расстоя-

ние между фокусами 2с=26;

7) расстояние между директрисами равно 32/5, а ось 2b=6;

8) расстояние между директрисами равно 8/3, а эксцентри-

ситет

ε=3/2;

9) уравнения асимптот у=

±3х/4, а расстояние между ди-

ректрисами равно 12,8.

18.

Дана гипербола .144916

22

=− yx Найти:

1) полуоси а и b;

2) фокусы;

3) эксцентриситет;

4) уравнения асимптот;

5) уравнения директрис.

19.

Фокусы гиперболы совпадают с фокусами эллипса

х

2

/25 + y

2

/9 = 1. Составить уравнение гиперболы, если ее

эксцентриситет

ε=2.

20.

Доказать, что расстояние от фокуса гиперболы

х

2

/а

2

- y

2

/b

2

= 1 до ее асимптоты равно b.

21.

Доказать, что произведение расстояний от любой точки

гиперболы

1

2

=−

b

y

a

x

до двух ее асимптот есть величина по-

стоянная, равная

22

ba

+

.

22.

Доказать, что площадь параллелограмма, ограниченно-

го асимптотами гиперболы

1

2

=−

b

y

a

x

и прямыми, проведен-

ными через любую ее точку параллельно асимптотам, есть ве-

личина постоянная, равная

2

ab

.

23.

Вывести условие, при котором прямая y=kx+m касает-

ся гиперболы

1

2

=−

b

y

a

x

.

75 76

24. Составить уравнение касательной к гиперболе

1

2

=−

b

y

a

x

в ее точке М(х; у).

25.

Составить уравнения касательных к гиперболе

х

2

- y

2

= 16, проведенных из точки А(-1; -7).

26.

На гиперболе 1

1824

22

=−

yx

найти точку М, ближайшую к

прямой 3х+2у+1=0. Вычислить расстояние d от точки М до

этой прямой.

27.

Составить уравнение параболы, вершина которой нахо-

дится в начале координат, зная, что:

1) парабола расположена в правой полуплоскости сим-

метрично относительно оси Ох, а ее параметр р=3;

2) парабола расположена в левой полуплоскости

симметрично относительно оси Ох, а ее параметр р=7;

3) парабола расположена в верхней полуплоскости

симметрично относительно оси Оу, а

ее параметр р=1/4;

4) парабола расположена в нижней полуплоскости

симметрично относительно оси Оу, а ее параметр р=3.

28.

Вывести условие, при котором прямая y=kx+b касается

параболы у

2

=2рх.

29.

Составить уравнение касательной к параболе у

2

=2рх в

точке М(х; у).

30.

Провести касательную к параболе у

2

= 12х параллельно

31.

прямой 3х-2у+30=0 и вычислить расстояние d между этой

касательной и данной прямой.

32.

Составить уравнения касательных к параболе у

2

=36х, про-

веденных из точки А(2; 9).

8. ВЕКТОРЫ В ПРОСТРАНСТВЕ

Определение. Вектором называется направленный отре-

зок. Если начало вектора находится в точке

А, а конец ― в

точке

В, то вектор обозначают

A

B

.

Для векторов используют также обозначения

.AB , , aa

Определение. Длина вектора

a

называется его модулем

и обозначается

a

. Единичным называется вектор

e

, для кото-

рого

1=e

.

Определение. Векторы a и b , лежащие на параллель-

ных прямых (или на одной и той же прямой), называются

кол-

линеарными

.

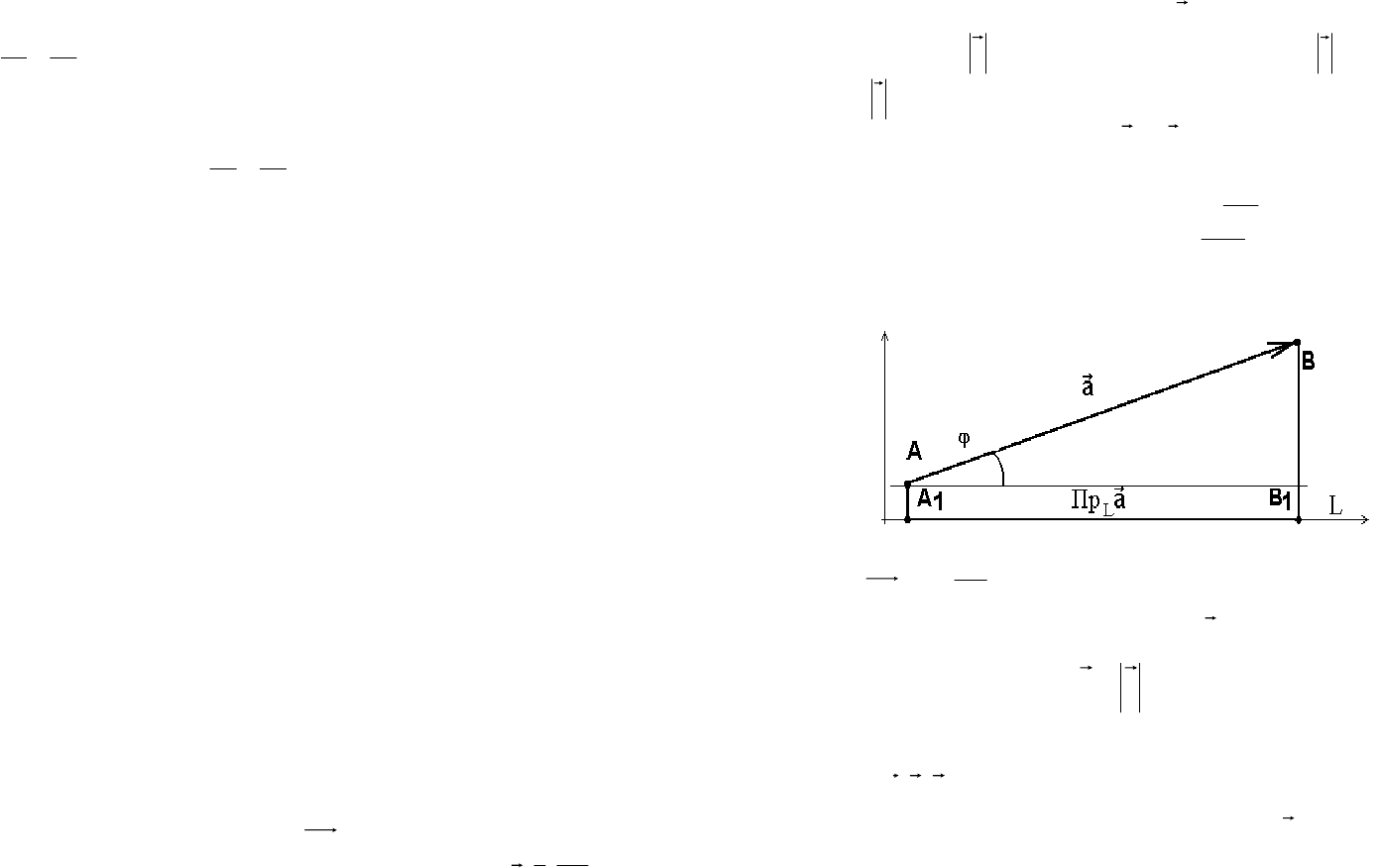
Определение. Проекцией вектора

A

B

на ось L называ-

ется число, равное величине отрезка

11

BA

оси L, где точка А

1

является проекцией на ось L точки А, а В

1

― проекцией на эту

ось точки

В.

Рисунок 13

Для проекции используют обозначения:

ABÏðABÏð

LL

,

.

Пусть

ϕ ― угол наклона вектора a к оси L. Тогда

.cos

ϕ

⋅= aaÏð

L

(1)

Пусть

Oxyz ― прямоугольная декартовая система коор-

динат,

kji ,,

- соответствующие единичные векторы, и пусть

х=ОМ

х

, у=ОМ

у

, z=ОМ

z

― проекции вектора a на соответст-

вующие координатные оси. Тогда

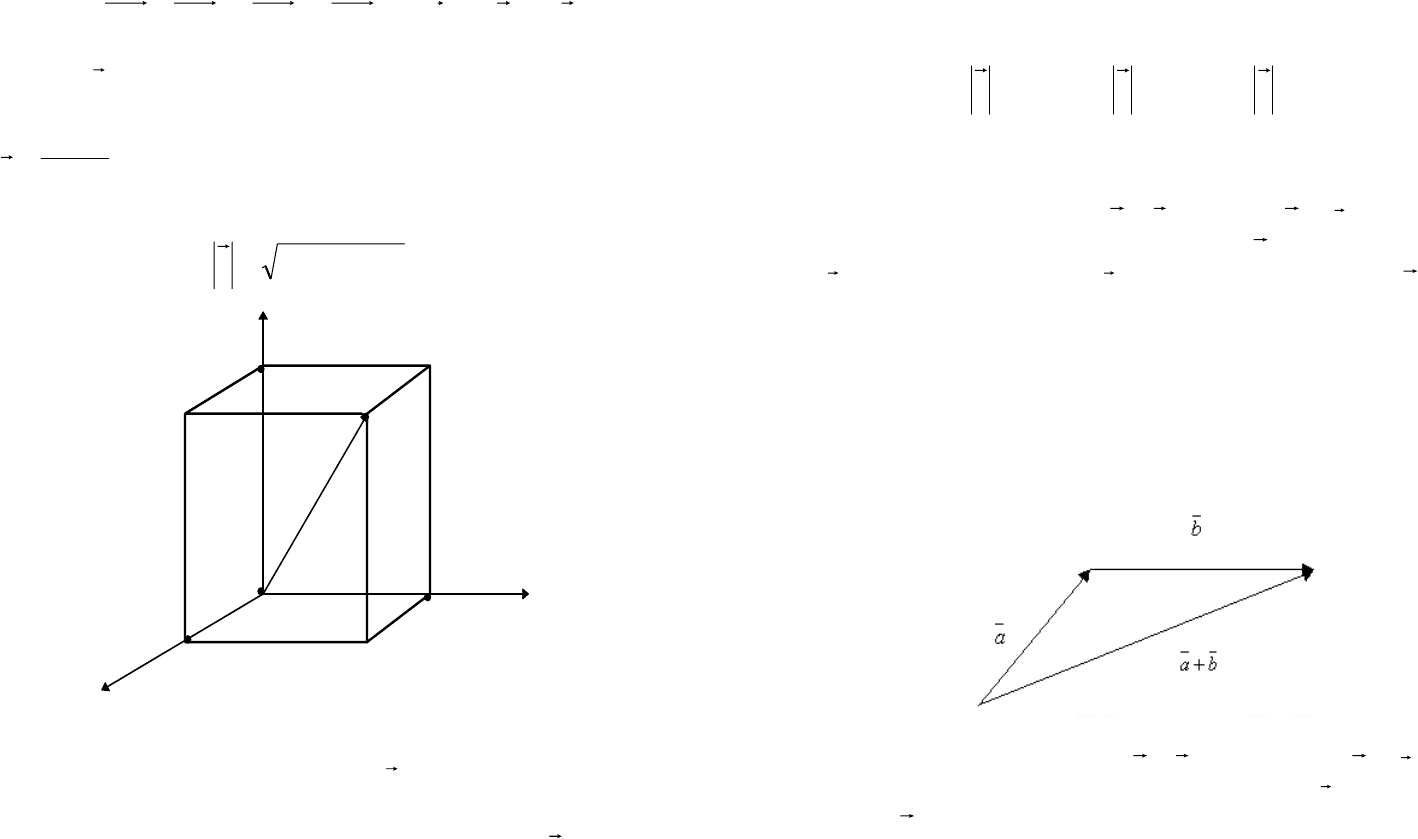
77 78

kzyyixOMOMOMOM

zyx

⋅+⋅+⋅=++=

и вектор

{}

zyxa ;;=

имеет декартовые координаты х, у, z.

Пусть

).z ;y ;( ),z ;y ;(

22221111

xMxM Тогда

{

}

{

}

zyxzzyyxxMMa ; ; ; ;

12121221

=−−−==

.

Формула

222

zyxa ++=

(2)

M

z

Z

Х0

М(х,у,z )

β

γ

α

М

у

М

х

Х

Рисунок 14

позволяет определить модуль вектора

{

}

zyxa ;;= по его коор-

динатам.

Пусть

α, β, γ ― углы, которые составляет вектор

a

с ко-

ординатными осями (рис. 14). Тогда

cosα, cosβ, cosγ ― на-

правляющие косинусы данного вектора. Из формулы (1)

следует:

.cos=z ,cos=y ,cos

γβα

⋅⋅⋅= aaax

Из последних равенств и формулы (2) следует, что

cos

2

α + cos

2

β + cos

2

γ =1.

Определение. Суммой

ba +

векторов

a

и

b

называет-

ся вектор, который идет из начала вектора

a

в конец вектора и

b

при условии, что вектор

b

приложен к концу вектора

a

.

Указанный способ сложения векторов называют

прави-

лом треугольника

(рис. 15).

 Наряду с правилом треугольника при сложении векто-

ров пользуются равносильным ему правилом паралле-

лограмма.

 Сложение произвольного конечного количества векто-

ров производится по модели последовательного при-

менения правила треугольника.

Рисунок 15

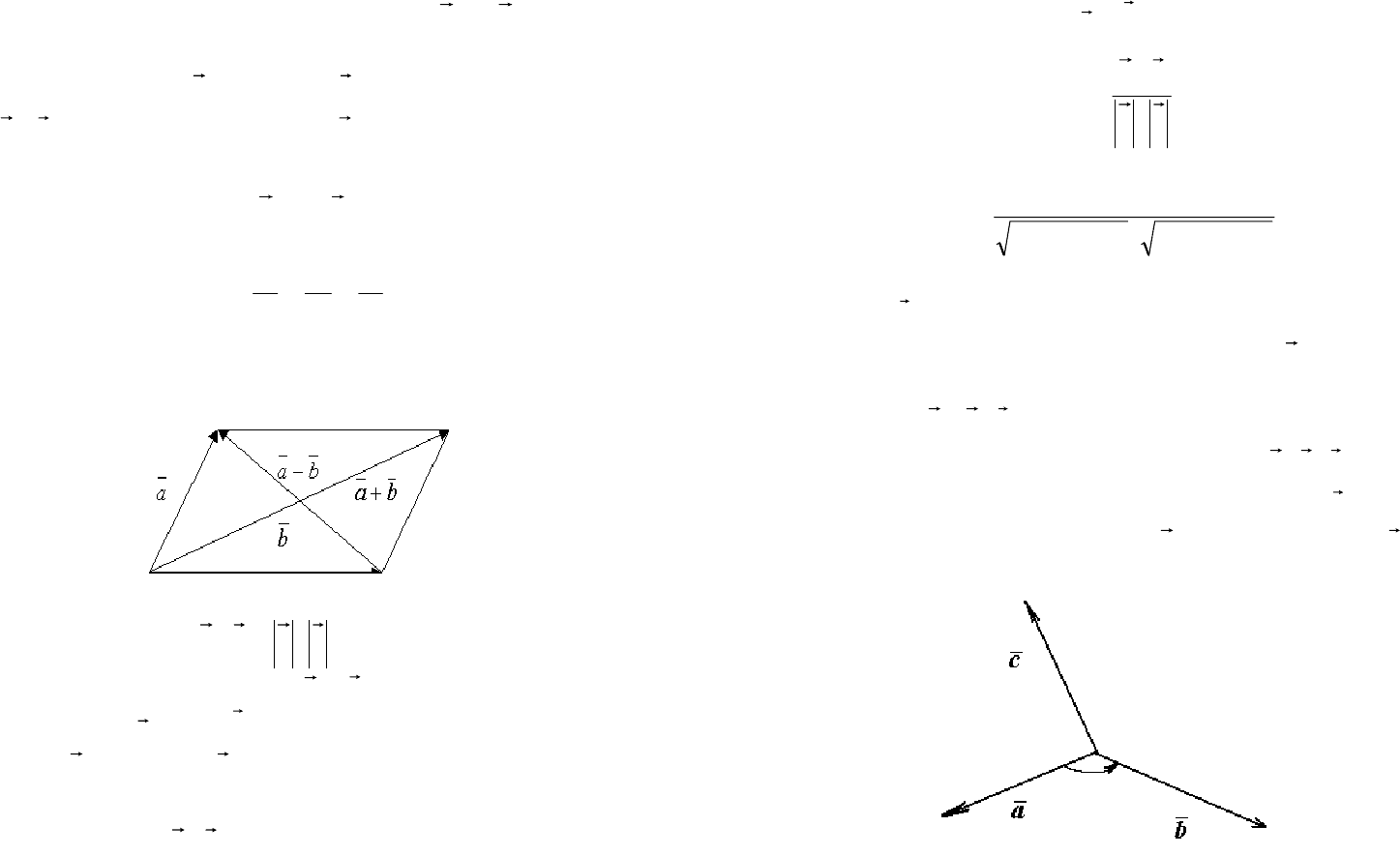
Определение. Разностью

ba −

двух векторов

a

и

b

на-

зывается вектор, который в сумме с вектором

b

составляет

вектор

a

.

Определение

. Два вектора равной длины, лежащие на од-

ной прямой и направленные в противоположные стороны, на-

79 80

зываются взаимообратными и обозначаются

a

и -

a

соответ-

ственно.

Если

{}{}

222111

; ; , ; ; zyxbzyxa ==

, то

{}

{

}

111212121

; ; , ; ; zyxazzyyxxba

λλλλ

=±±±=±

(рис. 16).

 Необходимым и достаточным условием коллинеарно-

сти двух векторов

a

и

b

является пропорциональ-

ность их координат:

.

2

1

2

1

2

1

z

y

x

==

Определение

. Скалярным произведением двух векторов

называется число, равное произведению модулей этих векто-

ров на косинус угла между ними, то есть,

Рисунок 16

,cos

ϕ

⋅⋅=• baba

где

ϕ ― угол между векторами

a

и

b

.

 Если a и b заданы своими координатами

{}{}

222111

; ; , ; ; zyxbzyxa ==

, то их скалярное произ-

ведение может быть вычислено по формуле:

212121

zzyyxxba ++=•

.

Угол между векторами a и b определяется по формуле:

ba

⋅

•

=

ϕ

cos

или в координатной форме:

.cos

2

1

2

1

2

1

332211

zyxzyx

yxyxyx

++⋅++

+

=

ϕ

Пусть ось

L образует углы

α

,

β

,

γ

с координатными

осями и

{

}

γβα

cos ;cos ;cos=e

― единичный вектор на

этой оси. Тогда проекция произвольного вектора

{}

zyxa ; ;=

на ось

L определяется формулой

γβα

coscoscos ⋅+⋅+⋅=•= zyxeaaÏð

L

.

Определение. Три коллинеарных вектора

cba , ,

обра-

зуют правую тройку, если с конца третьего вектора

c

крат-

чайший поворот от первого вектора

a

ко второму вектору

b

виден совершающимся против часовой стрелки (рис. 17).

Рисунок 17

Пчельник В.К. Пособие по курсу высшая математика. Матрицы и определители

Подождите немного. Документ загружается.