Пчельник В.К. Пособие по курсу высшая математика. Матрицы и определители
Подождите немного. Документ загружается.


141 142
б) 8 2 2 4 4 5 8 5 7 1
12.26 а) 1 6 3 2 1 6 7 8 4 5
б) 5 1 1 6 2 0 7 6 8 8
12.27 а) 6 6 6 6 3 2 8 5 2 4
б) 2 1 0 6 0 3 2 0 5 3
12.28 а) 6 2 0 5 1 5 5 8 6 8
б) 8 8 5 3 4 4 6 8 6 4
12.29 а) 8 0 8 7 3 8 5 1 6 5
б) 3 1 7 6 0 6 0 6 3 2
12.30 а) 2 2 1 0 8 7 2 0 4 8
Экзаменационная программа по линейной алгебре
1. Матрицы и линейные операции над ними. Умножение мат-
рицы на вектор. Преобразования матриц.
2.
Определители квадратных матриц и их свойства. Методы
вычисления определителей.
3.
Миноры и алгебраические дополнения. Теорема Лапласа и
теорема аннулирования.
4.
Обратная матрица, ее существование, построение и свойст-
ва.
5.
Системы линейных алгебраических уравнений. Системы с
невырожденной квадратной матрицей и способы их решения
(метод Крамера, матричный метод).
6.
Метод Гаусса решения систем линейных алгебраических
уравнений.
7.
Ранг матрицы и его вычисление. Теорема о базисном мино-
ре.
8.
Совместность линейных систем. Теорема Кронекера-
Капелли.
9.
Однородные системы линейных алгебраических уравнений.
Ненулевое решение однородной системы. Фундаментальная
система решений однородной системы и ее нахождение.
10.
Собственные векторы и собственные значения матриц и их
свойства.
11.
Контрольная работа.
Экзаменационная программа по основам аналити-
ческой геометрии
1. Векторы. Линейные операции над векторами. Проекция век-
тора на ось и ее свойства. n-мерное векторное пространство.
2.
Скалярное произведение векторов, его физический смысл и
свойства. Координатная форма скалярного произведения. Ус-
ловие перпендикулярности двух векторов.
3.
Векторное произведение векторов, его геометрический и
физический смысл. Свойства векторного произведения. Коор-
динатная форма векторного произведения. Условие коллине-
арности двух векторов.
4.
Смешанное произведение векторов, его геометрический
смысл и свойства. Координатная форма смешанного произве-
дения. Условие компланарности трех векторов.
5.
Линейная зависимость и независимость системы векторов.
Примеры. Базис системы векторов и n-мерного векторного
пространства. Координаты вектора в базисе.
6.
Прямая на плоскости. Различные виды уравнения прямой (с
угловым коэффициентом, по точке и угловому коэффициенту,
через две точки, общее, каноническое, параметрическое).
7.
Нормальное уравнение прямой на плоскости.
8.
Условие параллельности и перпендикулярности двух пря-
мых на плоскости. Угол между двумя прямыми.
9.
Эллипс. Каноническое уравнение, исследование формы,
параметры эллипса, директрисы эллипса.
143 144
10. Гипербола. Каноническое уравнение, исследование формы
и расположение ветвей относительно осей координат, парамет-
ры гиперболы, директриса и асимптоты гиперболы.
11.
Парабола. Каноническое уравнение, исследование формы,
параметр параболы, директриса параболы. Различное располо-
жение параболы относительно системы координат.
12.
Различные виды уравнения плоскости в пространстве (об-
щее, через три точки, через точку по известному нормальному
вектору, через точку параллельно двум векторам).
13.
Нормальное уравнение плоскости. Расстояние от точки до
плоскости.
14.
Прямая в пространстве. Каноническое, параметрическое,
общее уравнение прямой в пространстве.
15.
Условия параллельности и перпендикулярности двух пря-
мых, двух плоскостей, прямой и плоскости. Угол между двумя
плоскостями, двумя прямыми, прямой и плоскостью.
16.
Поверхности второго порядка: эллипсоид, гиперболоиды и
параболоиды, конус, цилиндры. Исследование формы методом
сечений.
ПРИЛОЖЕНИЕ 1
Формулы для выполнения матричных операций с
использованием электронных таблиц Microsoft
Excel
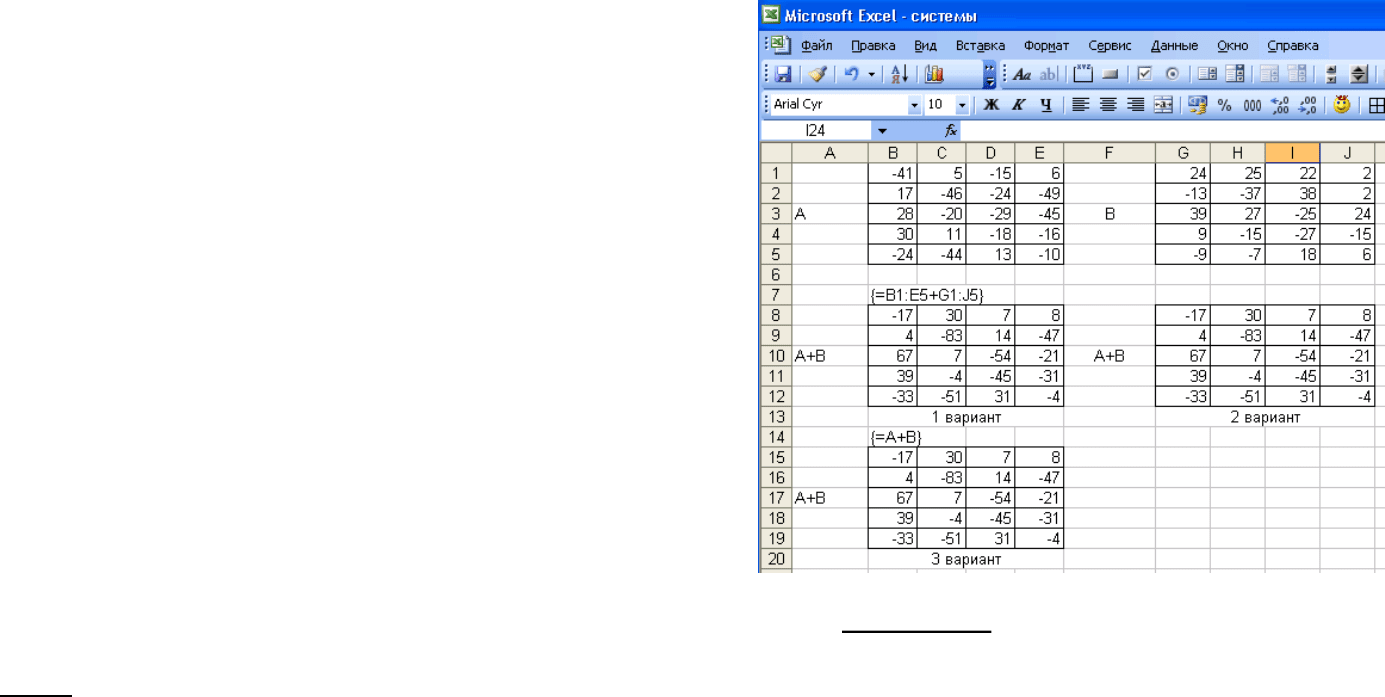
Сумму двух матриц А и В можно найти с использова-
нием табличной формулы {=B1:F5+G1:J5} (1 вариант) либо
копированием содержимого ячейки G7, содержащей сумму
B1+G1, на остальной диапазон размещения суммы (2 вариант)
(заданные матрицы А и В располагаются в диапазонах B1:E5 и
G1:J5 соответственно на рис. 19). В третьем варианте исполь-
зуется табличная формула, причем предварительно диапазонам
B1:E5 и G1:J5
присвоены имена А и В соответственно.
Рисунок 19
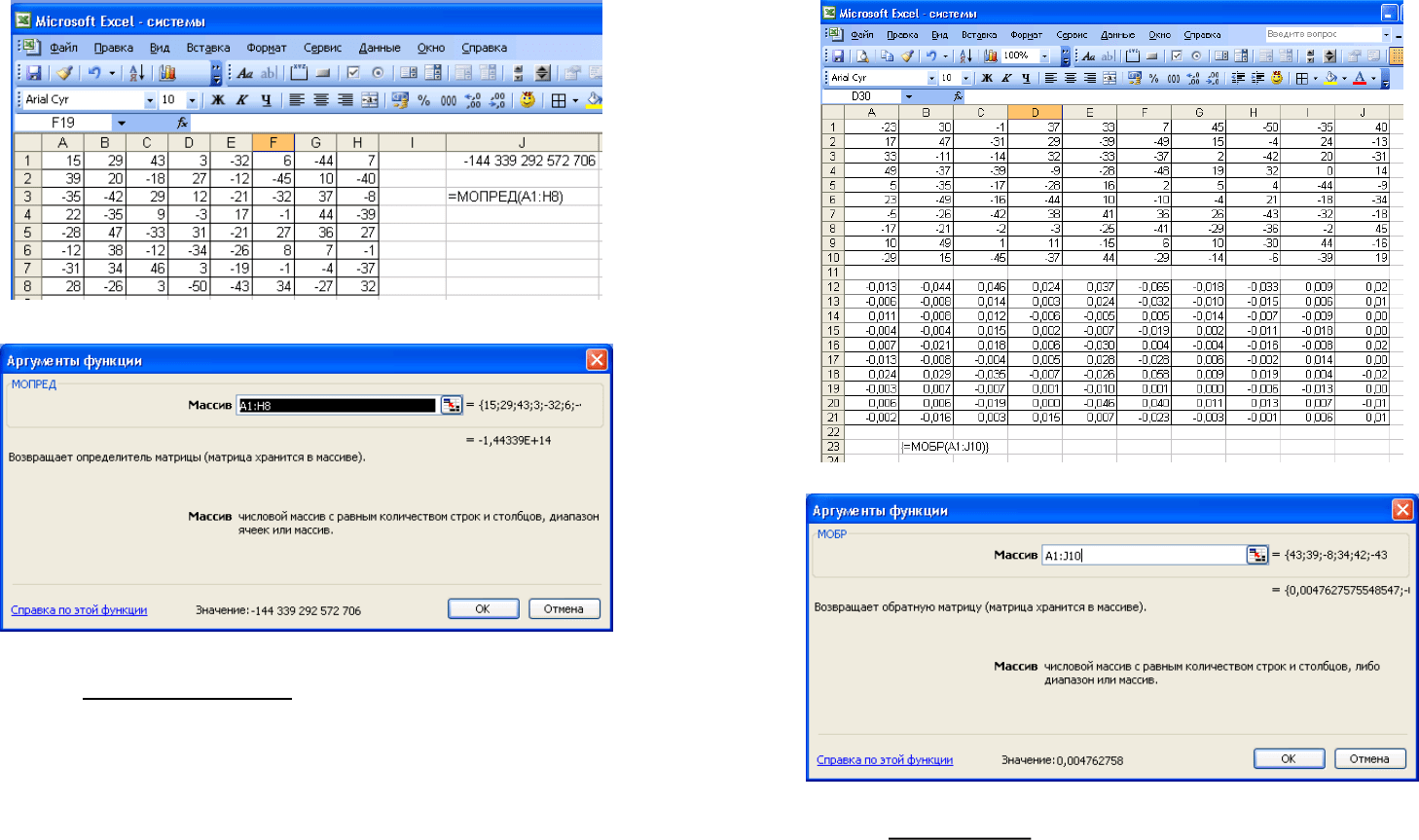
Определитель квадратной матрицы А, можно найти с
использованием функции МОПРЕД (на рис. 20 матрица А рас-
полагается в диапазоне А1:Н8). На рис. 21 показано окно диа-
лога функции МОПРЕД.
145 146
Рисунок 20
Рисунок 21
Обратную матрицу для невырожденной матрицы
можно найти с использованием табличной функции МОБР (на
рис. 22 матрица А расположена в диапазоне А1:J10). На рис. 23
показано окно диалога функции МОБР.
Рисунок 22
Рисунок 23
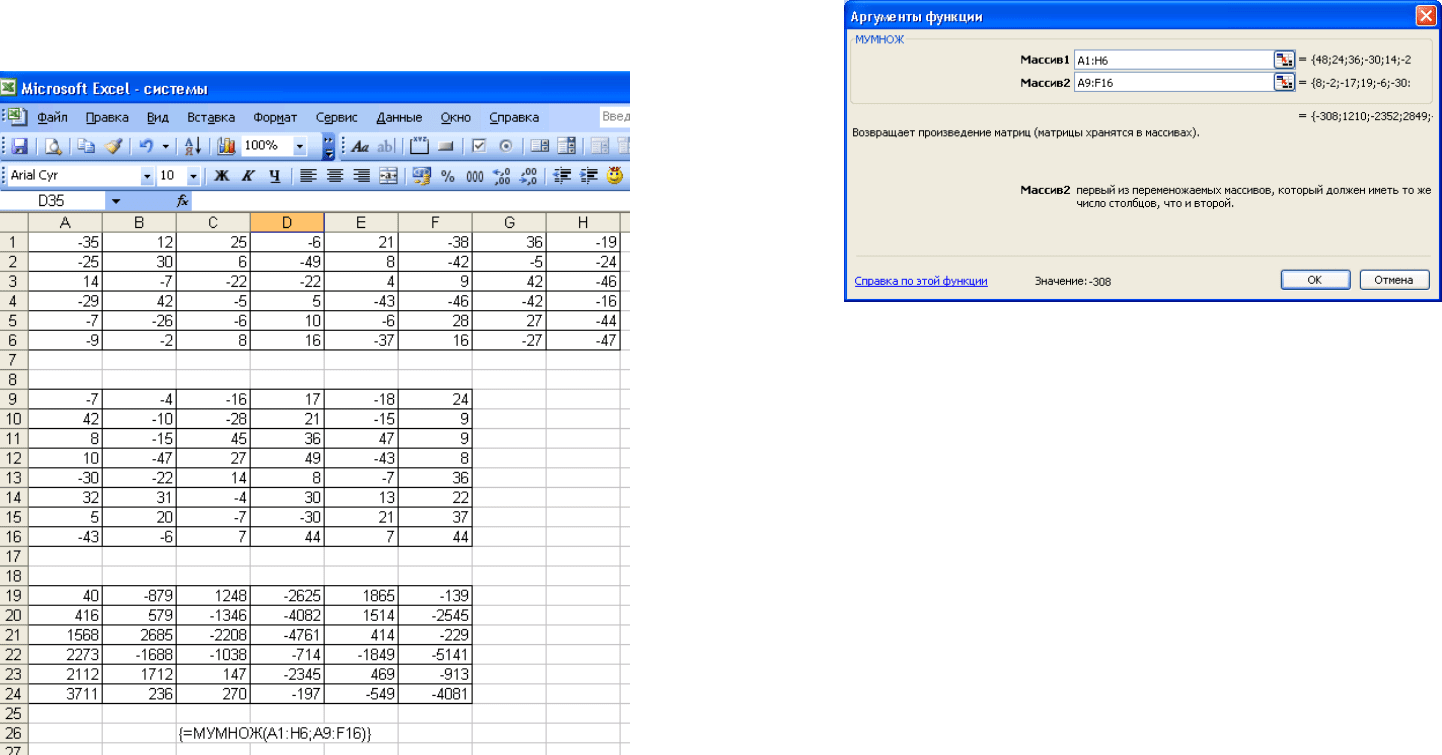
Произведение двух матриц А и В можно найти, ис-
пользуя табличную функцию МУМНОЖ (на рис.24 матрицы А
147 148
и В располагаются в диапазонах А1:H6 и A9:F16 соответствен-
но): На рис. 25 показано окно диалога функции МУМНОЖ.
Рисунок 24
Рисунок 25
Чтобы решить матричное уравнение АХ=В, можно
воспользоваться табличной формулой
{=МУМНОЖ(МОБР(A1:H8);J1:J8)}
(на рис. 26 матрица А расположена в диапазоне A1:H8, а мат-
рица В – в диапазоне J1:J8). Результат расположен в диапазоне
А10:А17. Для контроля выполнено умножение матрицы А на
матрицу Х. Результат расположен в диапазоне J10:J17 и он
совпадает с матрицей В
.

149 150
Рисунок 26
ПРИЛОЖЕНИЕ 2
Построение графиков функций на плоскости с
использованием электронных таблиц Microsoft
Excel
Для построения кривой иногда удобно воспользоваться
представлением точки на плоскости либо в полярной системе
координат, либо с использованием параметра.
Рассмотрим полярную систему координат. Для ее опре-
деления надо задать на плоскости:
1. масштаб (т.е. единицу измерения длины);
2. направление вращения в плоскости. Примем его поло-
жительным, если оно направлено против часовой
стрелки;
3. точку О, называемую «началом» или полюсом системы
координат;
4. полупрямую Ор, исходящую из точки О (рис. 27) (эта
полупрямая называется полярной осью). Положительное на-
правление на полупрямой задается вектором
OE (где Е - лю-
бая ее точка, отличная от точки О).
Рисунок 27 Рисунок 28 Рисунок 29
Если таким образом выбрана полярная система коорди-
нат, то для каждой точки М плоскости (рис. 28) определены ее
полярные координаты, а именно:
1) угол наклона φ вектора
OM к полярной оси;
2) расстояние ρ точки М от начала О (т.е. длина вектора
OM ).
Угол φ называется полярным углом точки М или первой
полярной координатой этой точки (0≤ φ≤2π). Число ρ называ-
ется полярным радиусом или второй полярной координатой
точки М. Полярный радиус любой точки М, отличной от О,
положителен; для точки О он равен нулю.
Декартову систему координат Оху выберем так, чтобы
начало координат О совпало с полюсом О, а ось абсцисс со-
вместим с полярной осью. Ось ординат определяем как ось, в
которую перейдет полярная ось при повороте ее вокруг полюса
О на угол φ в положительном направлении. Тогда из прямо-
угольного треугольника ОАМ получаем формулы, связываю-
151 152
щие полярные и декартовы координаты:
⎩
⎨
⎧
=
=
)sin(
);cos(
ϕρ
ϕρ
y
x
(рис. 29).
При использовании параметрического представления
кривой используют систему вида
⎩
⎨
⎧
=
=
).(
);(
tyy
txx
где t пробегает некоторый диапазон значений.
Для изображения кривых на плоскости выполняем
последовательность действий:
а).
подготовим диапазон изменения угла φ (переменной t);
б).
рассчитаем значения функции на данном диапазоне в
полярных координатах ρ=ρ(φ) (в случае использования
полярной системы координат);
в).
рассчитаем значения х и y в декартовой системе координат:
)sin( ),cos(
ϕ
ρ
ϕ
ρ
=
= yx (в случае использования полярной
системе координат) или
⎩
⎨
⎧
=
=
)(
);(
tyy
txx
при использовании пара-
метрического представления;
г).
выделим диапазон области определения и области
значений функции и воспользуемся Мастером построения
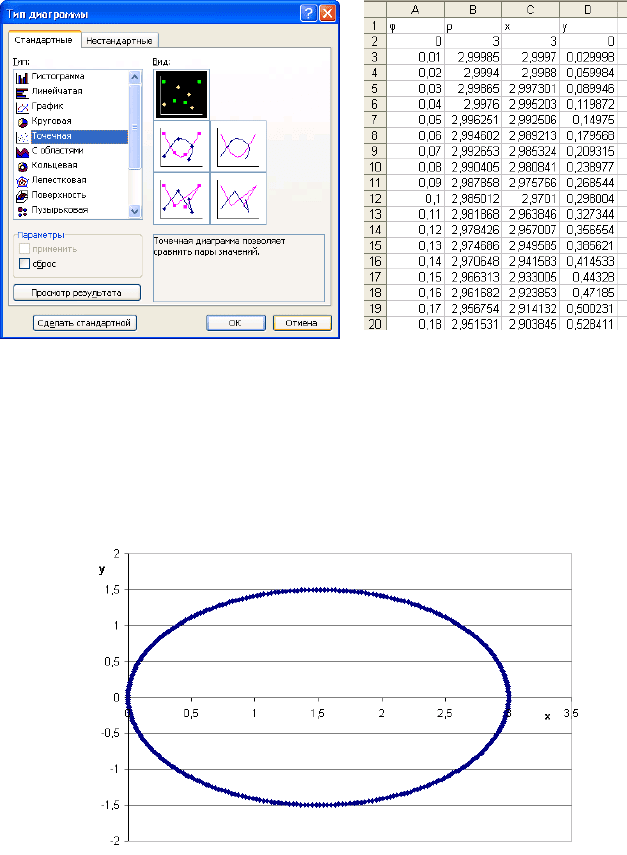
диаграмм. В качестве типа диаграммы удобно выбрать тип
Точечная (рис.30).
Рисунок 30
Рисунок 31
Приведем примеры построения некоторых кривых.
Уравнение эллипса в полярных координатах имеет вид
ρ=acos(φ). Пусть для примера a=3, b=5. На рис. 31 приведен
фрагмент таблицы, по столбцам x и y которой построена
точечная диаграмма, приведенная на рис. 32.
Рисунок 32
153 154
В таблице 18 приведены некоторые кривые, простроен-
ные аналогичным путем с использованием полярной системы
координат либо с использованием параметрического представ-
ления кривой.
Таблица 18
Название и уравнение
кривой
Вид кривой
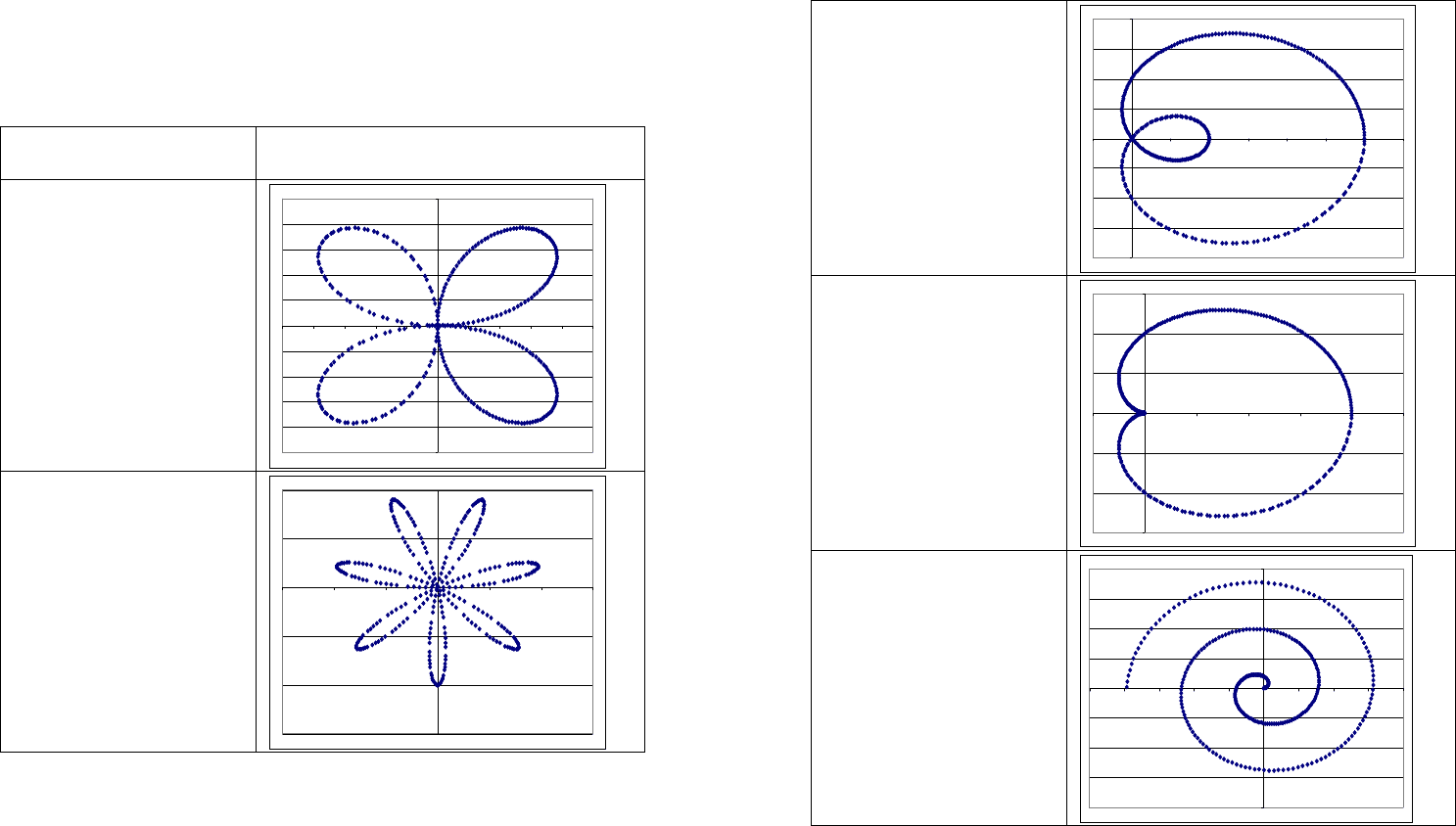
Четырехлепестковая
роза
ρ=sin(2φ)
-1
-0,8
-0,6
-0,4
-0,2
0
0,2
0,4
0,6
0,8
1
-1 -0,8 -0,6 -0,4 -0,2 0 0,2 0,4 0,6 0,8 1
Семилепестковая роза
ρ=sin(7φ)
-1,5
-1
-0,5
0
0,5
1
-1,5 -1 -0,5 0 0,5 1 1,5
Улитка Паскаля
ρ=1+2cos(φ)
-2
-1,5
-1
-0,5
0
0,5
1
1,5
2
-0,5 0 0,5 1 1,5 2 2,5 3 3,5
Кардиоида
ρ=1+cos(φ)
-1,5
-1
-0,5
0
0,5
1
1,5
-0,5 0 0,5 1 1,5 2 2,5
Спираль Архимеда
ρ=φ/4
-4
-3
-2
-1
0
1
2
3
4
-5 -4 -3 -2 -1 0 1 2 3 4
155 156
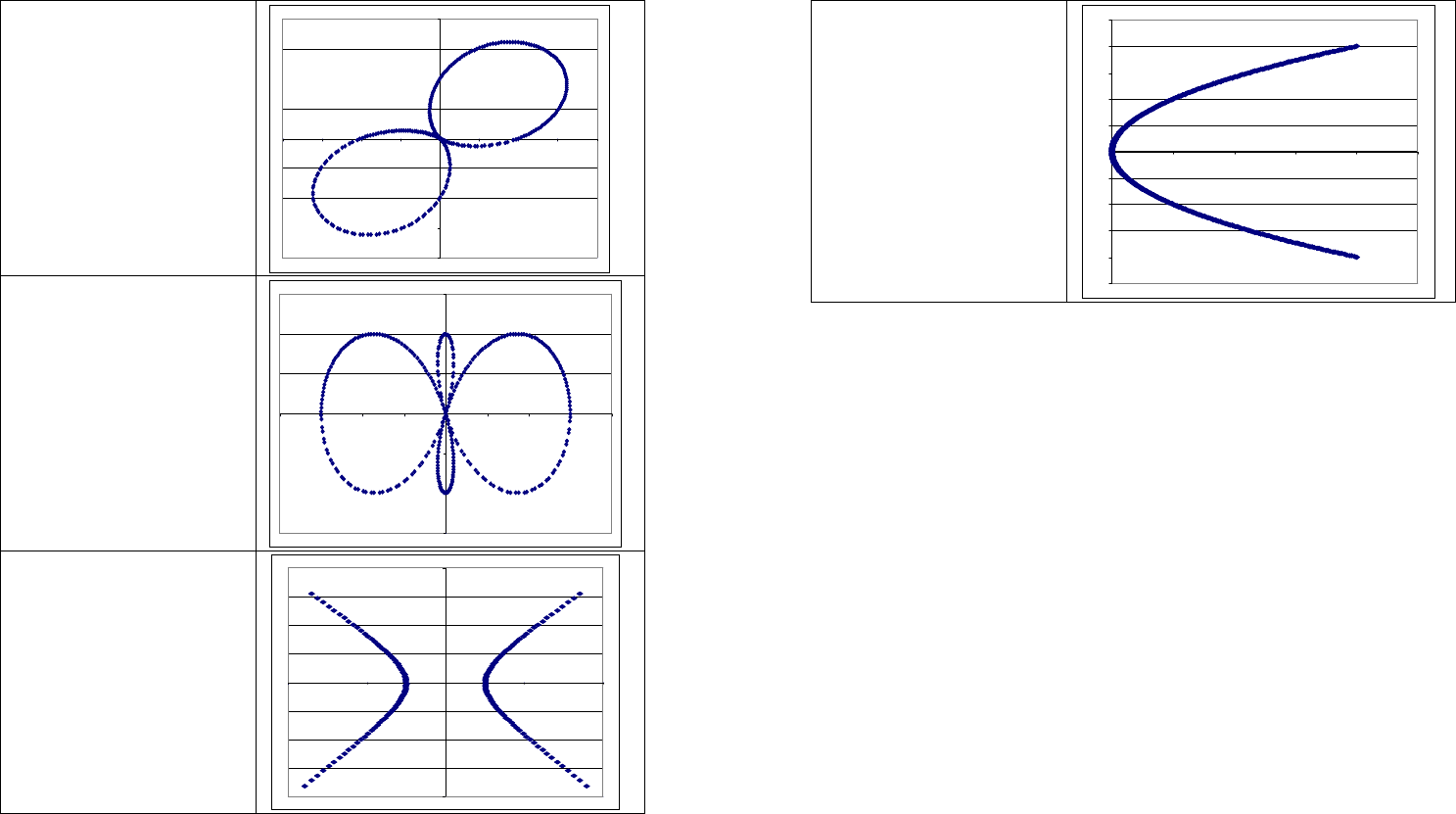
Двухлепестковая роза
ρ=1+sin(2φ)
-2
-1,5
-1
-0,5
0
0,5
1
1,5
2
-2 -1,5 -1 -0,5 0 0,5 1 1,5 2
Петельное сцепление
ρ=1+2cos(2φ)
-1,5
-1
-0,5
0
0,5
1
1,5
-4 -3 -2 -1 0 1 2 3 4
Гипербола
∞<<∞−
±=
⎩
⎨
⎧
⋅=
⋅⋅=
t
tshby
tchax
,1
)(
);(
ε
ε
-4
-3
-2
-1
0
1
2
3
4
-4 -2 0 2 4
Парабола
∞<<∞−
⎩
⎨
⎧
⋅⋅=
⋅⋅=
t
tpy
tpx
2
;2
2
-5
-4
-3
-2
-1
0
1
2
3
4
5
0246810
ПРИЛОЖЕНИЕ 3
Построение поверхностей с использованием
электронных таблиц Microsoft Excel
Мастер диаграмм позволяет строить следующие подтипы
поверхностных диаграмм:
1.
трехмерные стандартные;
2.
трехмерные проволочные;
3.
контурные;
4.
контурные проволочные.
Первый подтип отображает изменение значения по двум
измерениям в виде поверхности. Второй подтип строит про-
зрачную поверхность, заполненную сеткой, отображающей
линии одинаковых значений. Третий подтип дает вид сверху
стандартной диаграммы. Четвертый подтип дает вид сверху
проволочной диаграммы.
Для построения диаграммы следует установить интерва-
лы изменения переменных x и y. Так, например
, для построе-
ния поверхности
(
)
22
cos yxz += будем рассматривать для
переменных x и y интервалы от –1,5 до 1,5 включительно с
шагом 0,2. Заполним ячейки В1:Q1 и А2:А17 значениями от –
1,5 до 1,5 с шагом 0,2 (оси OY и ОХ соответственно). Можно

157 158
присвоить этим диапазонам имена X и Y соответственно. В
диапазон В2:Q17 поместим формулу
{=COS(X*X+Y*Y)}.
Используя мастер диаграмм, получаем поверхность, изобра-
женную на рис. 33.
-1,50
-1,10
-0,70
-0,30
0,10
0,50
0,90
1,30
-1,50
-0,30
0,90
-1,00
-0,80
-0,60
-0,40
-0,20
0,00
0,20
0,40
0,60
0,80
1,00
Рисунок 33
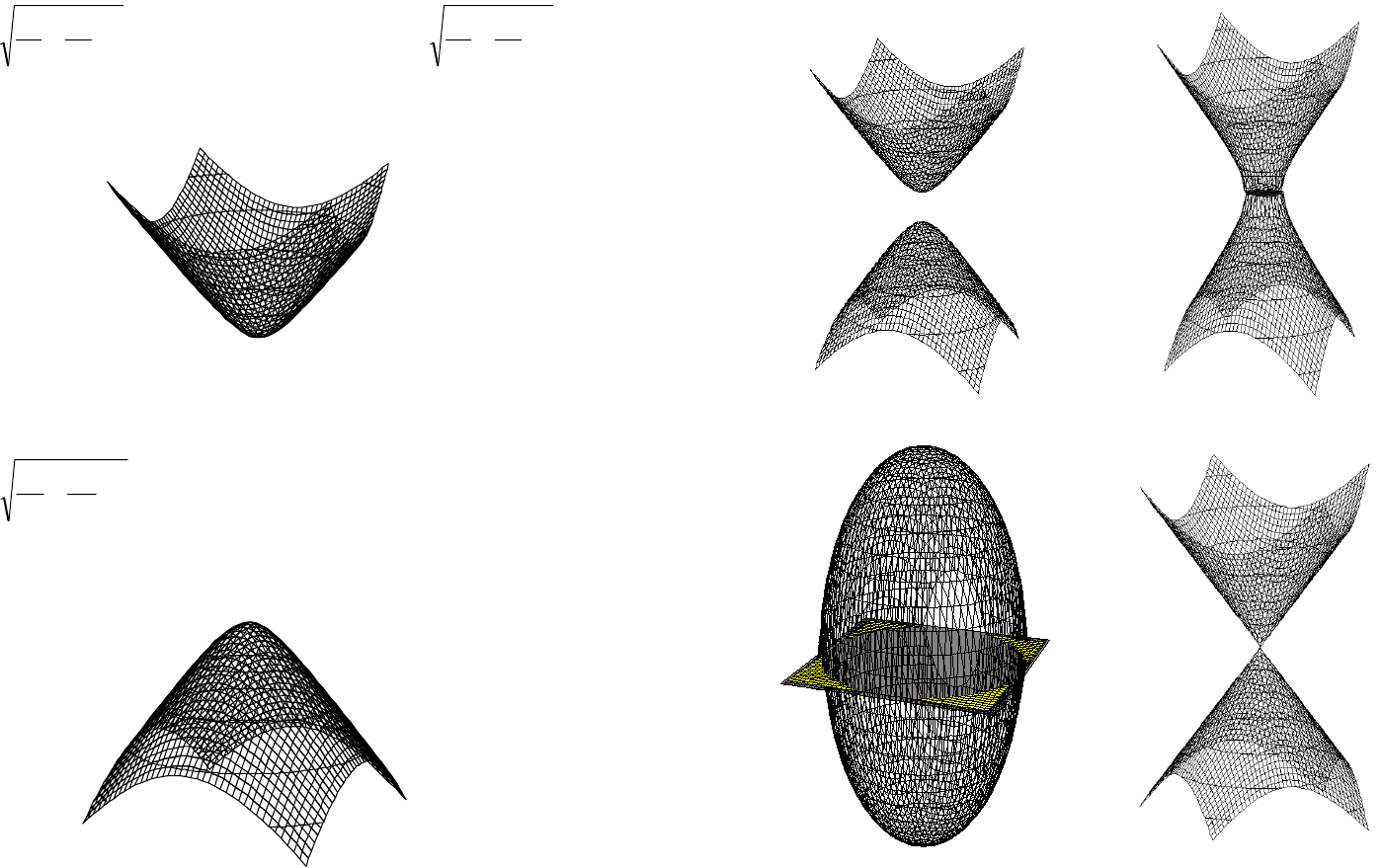
Аналогичным путем получены эллиптический параболо-
ид (рис. 34), гиперболический параболоид (рис. 35).
Рисунок 34
Рисунок 35
Для получения изображения однополостного гипербо-
лоида
преобразуем выражение 1
2
2
2
2
2
2
=−+
c
z
b
y
a
x
к виду
159 160
1
2
2
2
2
−+±=
b
y
a
x
cz . Построим поверхность 1
2
2
2
2
−+=
b
y
a
x
cz
(рис. 36). Сделаем прозрачными боковые стенки диаграммы и
удалим линии сетки.
Рисунок 36
Вторую часть поверхности построим копированием диа-
граммы, полученной на рис. 36, изменив формулу на
1
2
2
2
2
−+−=
b
y
a
x
cz (рис. 37). Затем накладываем диаграммы и
получаем изображение, приведенное на рис. 38.
Изображения однополостного гиперболоида (рис. 39),
эллипсоида (рис. 40) и конуса (рис. 41) получены аналогично.
Рисунок 37
Рисунок 38 Рисунок 39
Рисунок 40 Рисунок 41
