Пчельник В.К. Пособие по курсу высшая математика. Матрицы и определители

41 42

5. ДЕКАРТОВЫ ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ

НА ПЛОСКОСТИ

Определение. Декартовой прямоугольной системой ко-

ординат

называются две взаимноперпендикулярные прямые

оси, занумерованные в каком-либо порядке, с заданными на

них одинаковыми единичными отрезками.

Точка пересечения осей

О называется началом коорди-

нат

, а сами оси ― координатными осями. Первая из них назы-

вается осью

абсцисс (ось Ох), вторая ― осью ординат (ось

Оy).

Y

M

y

M

0 M

x

X

Рисунок 6

Координатами произвольной точки М в заданной системе

координат называются числа

х=ОМ

x

, y=ОМ

y

, где М

x

, М

y

―

проекции точки

М на оси Ох и Оy соответственно (рис. 6). За-

пись

М(х;y) обозначает, что точка М имеет координаты (х;y).

Расстояние

d между двумя точками М

1

(х

1

;y

1

) и М

2

(х

2

;y

2

)

определяется по формуле

.)()(

2

12

2

12

yyxxd −+−=

Если точка

М(х;y) лежит на прямой, проходящей через

точки

М

1

(х

1

;y

1

), М

2

(х

2

;y

2

) и дано отношение

λ

=М

1

М/ММ

2

(

λ≠

-1), в котором точка М делит отрезок М

1

М

2

, то координаты

точки

М определяются по формулам

λ

+

=

1

21

хх

х

, .

1

21

λ

+

=

yy

y

Если точка М - середина отрезка М

1

М

2

, то ее координа-

ты определяются по формулам

2

21

хх

х

+

= ,

2

21

yy

y

+

= .

Для любых трех точек А(х

1

;у

1

), В(х

2

;у

2

), С(х

3

;у

3

) площадь

S треугольника

АВС вычисляется по формуле:

.mod

2

1

2

1

mod

1212

1313

1212

1313

yyxx

S

−−

=

−−

=

5.1. Примеры решения типовых задач

Пример 1. Найти координаты проекций на ось абсцисс и

ось ординат точек А(7;-5) и В(-2;3).

Решение. Так как х=ОМ

x

и y=ОМ

y

, где М

x

и М

y

― проек-

ции точки М(х;y) на оси Ох и Оy соответственно, то: А

x

(7),

А

y

(-5),

В

x

(-2), В

y

(3).

Ответ: А

x

(7), А

y

(-5), В

x

(-2), В

y

(3).

Пример 2. Найти координаты точек, симметричных точке

А(α;β) относительно осей Ох, Оy и начала координат.

Решение. По определению точка М* будет симметричной

точке М(х;y) относительно оси, если она одинаково удалена от

оси и лежит по другую сторону от нее (см. рисунок). Поэтому

координаты симметричных точек будут равны

соответственно

А

1

(α;-β), А

2

(-α;β), А

3

(-α;-β).

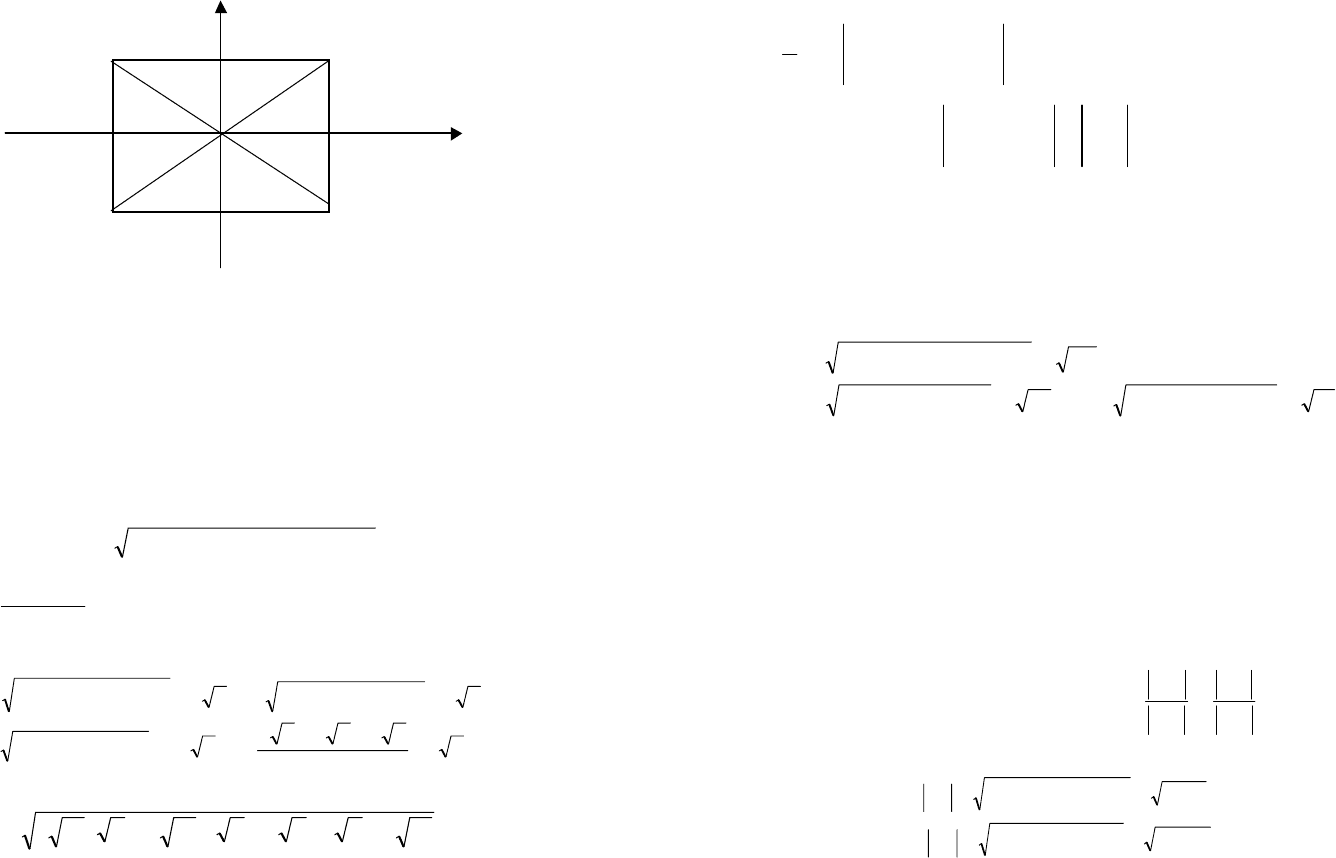
43 44

Ответ: А

1

(α;-β), А

2

(-α;β),А

3

(-α;-β).

Y

M

2

(-x;y) M(x;y)

0 X

M

3

(-x;-y) M

2

(x;-y)

Рисунок 7

Пример 3. Выяснить, лежат ли указанные точки

М

1

(2;3),М

2

(5;6) и М

3

(7;8) на одной прямой.

Решение. Точки М

1

(x

1

,y

1

),,М

2

(x

2

,y

2

), М

3

(x

3

,y

3

) лежат на

одной прямой тогда и только тогда, когда площадь треуголь-

ника М

1

М

2

М

3

рана нулю.

Способ 1. Вычислим площадь треугольника по трем сторонам,

используя формулу Герона:

,)()()( cpbpappS −⋅−⋅−⋅=

где

cba

p ,, ,

2

+

=

― стороны данного треугольника. В

нашем случае

()

() ()()

()()

.25

2

232522

,233625

,253827,226857

2

222

2

=

++

==−+−=

=−+−==−+−=

pc

ba

Тогда

.0)2325)(2525()2225(25 =−−−=S

Следовательно, указанные точки лежат на одной прямой.

Способ 2. Найдем площадь треугольника по формуле

.mod

2

1

1212

1313

yyxx

S

−−

=

В нашем случае имеем:

.0

33

55

3625

3817

==

−−

Значит, указанные точки лежат на одной прямой.

Пример 4. Доказать, что треугольник с вершинами

А(2;-1), В(-3;4), С(5;2) прямоугольный.

Доказательство. Находим длины сторон треугольника

АВС:

()( )

()() ()

.18)12(95;684235=BC

;50)1(423

2

222

22

=++−==−++

=−−+−−=

AC

AB

Проверяем выполнение условия

222

cba =+

для сторон

треугольника. Имеем:

222

ACABBC += . По теореме, обрат-

ной теореме Пифагора, получаем, что треугольник АВС прямо-

угольный.

Пример 5. Даны вершины треугольника А(6;-6), В(2;-3),

С(8;5). Найти длину биссектрисы его внутреннего угла при

вершине С.

Решение. Пусть ВF ― биссектриса. По свойству биссек-

трисы внутреннего угла треугольника

.

λ

==

BC

AB

FC

AF

Нахо-

дим:

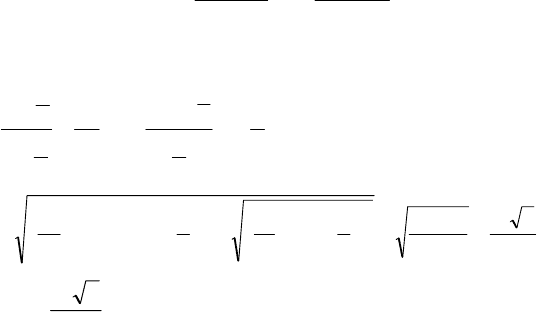
.106436)35()28(

,5916)63()62(

22

=+=−+−=

=+=+−+−=

BC

AB

45 46

Тогда

λ

=1/2. Координаты точки F(x;y) находим по фор-

мулам:

λ

+

=

+

=

1

,

1

2121

yy

y

xx

x

.

В нашем случае имеем (x

1

;y

1

)=(6;-6),(x

2

;y

2

)=(8;5),

.

3

7

2

3

5

6

,

3

26

2

1

2

8

6

−=

+−

==

+

= yx

Найдем длину BF:

.

3

210

9

4196

3

2

3

14

3

7

32

3

20

2222

=

+

=

⎟

⎠

⎞

⎜

⎝

⎛

−+

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

+−+

⎟

⎠

⎞

⎜

⎝

⎛

−=BF

Ответ:

.

3

210

5.2. Задачи для самостоятельного решения

1. Построить точки А(2;3), В(-5;1), С(-2;-3), D(0;3), E(-5;0),

F(-1/3;2/3).

2.

Найти координаты проекций точек А(2;-3), В(3;-1),

С(-5;1), D(-3;-2), E(-5;-1) на оси абсцисс и ординат.

3.

Найти координаты точек, симметричных относительно осей

Ох и Оy точкам 1) А(2;3); 2) В(-3;2); 3) С(-1;-1);

4) D(-3;-5); 5)E(-4;6); 6) F(α;β).

4.

Найти координаты точек, симметричных относительно на-

чала координат точкам 1) А(3;3); 2) В(2;-4); 3) С(-2;1);

4) D(5;-3); 5) E(-5;-4); 6) F(α;β).

5.

Даны две смежные вершины квадрата А(3;-7) и В(-1;4). Вы-

числить его площадь.

6.

Даны две противоположные вершины квадрата Р(3;5) и

Q(1;-3). Вычислить его площадь.

7.

Даны три вершины А(3;-7), В(5;-7), С(-2;5) параллелограмма

АВСD, четвертая вершина D которого противоположна

вершине В. Определить длину диагоналей параллелограмма.

8.

Доказать, что точки А(3;-5), В(-2;-7) и С(18;1) лежат на од-

ной прямой.

9. Доказать, что треугольник с вершинами А(-3;-2), В(0;-1),

С(-2;5) прямоугольный.

10.Доказать, что точки А(2;2), В(-1;6), С(-5;3) и D(-2;-1) явля-

ются вершинами квадрата.

11.На оси Ох найти точку М, одинаково удаленную от начала

координат и от точки А(8;4).

12.Через точку А(4;2) проведена окружность, касающаяся обе-

их координатных осей. Определить ее центр и

радиус R.

13.Через точку М(1;-2) проведена окружность радиуса 5, ка-

сающаяся оси Ох. Определить ее центр.

14.Дан треугольник с вершинами А(-4;2), В(0;-1) и С(3;3). Оп-

ределить его площадь, периметр и углы.

15.Даны вершины треугольника А(1;-3), В(3;-5) и С(-5;7). Оп-

ределить середины его сторон.

16.Даны две точки А(3;-1) и В(2;1). Определить: 1) координаты

точки М, симметричной точке А относительно точки В;

2) координаты точки N, симметричной точке В относитель-

но точки А.

17.Точки М(2;-1), N(-1;4) и Р(-2;2) являются серединами сто-

рон треугольника. Определить его вершины.

18.Даны вершины треугольника А(1;4), В(3;-9), С(-5;2). Опре-

делить длину его медианы, проведенной из вершины В.

19.Даны вершины треугольника А(2;-5),

В(1;-2), С(4;7). Найти

точку пересечения со стороной АС биссектрисы внутренне-

го угла при вершине В.

20.Вычислить площадь треугольника, вершинами которого

являются точки: 1) А(2;3), В(3;2) и С(-2;5); 2) М

1

(-3;2),

М

2

(5;-2) и М

3

(1;3); 3) М(3;-4), N(-2;3) и Р(4;5).

21.Вершинами треугольника являются точки А(3;6), В(-1;3) и

С(2;-1). Вычислить длину его высоты, проведенной из вер-

шины С.

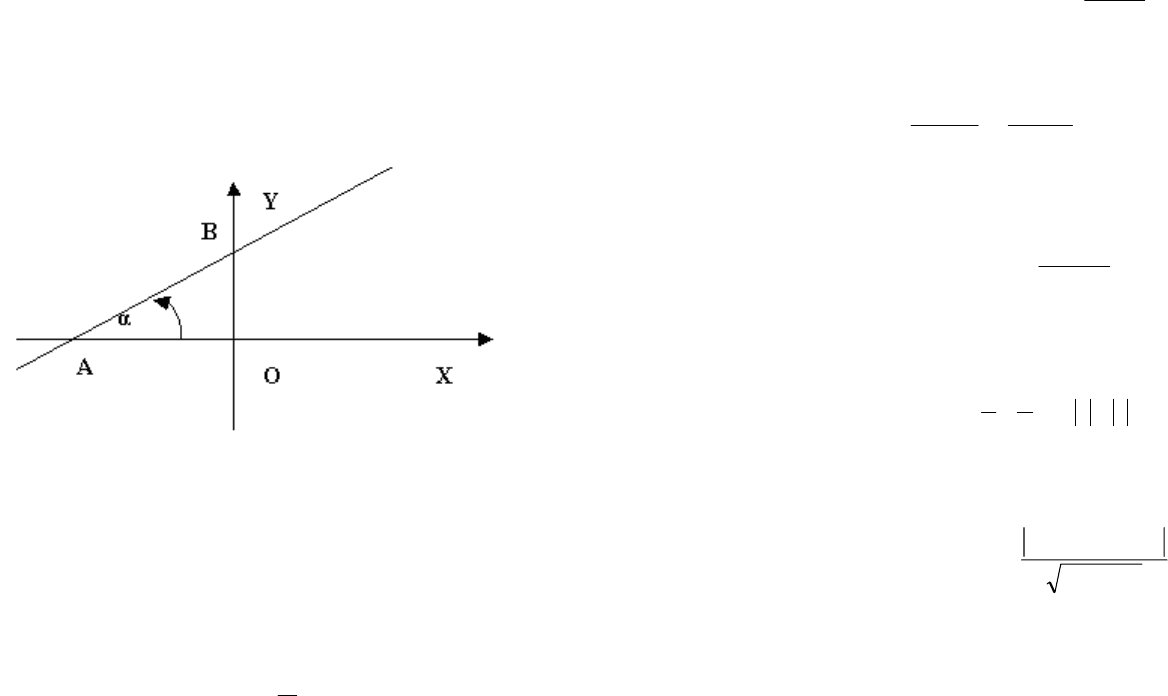
47 48

6. ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ

Определение. Уравнение вида

Ax + By + C = 0 (1)

называется общим уравнением прямой

).0(

22

≠+ BA

 В декартовых координатах любая прямая определяется

уравнением (1) и наоборот, любое уравнение (1) опре-

деляет прямую.

Определение. Угловым коэффициентом прямой называют

тангенс угла наклона ее к положительной полуоси Ох прямо-

угольной декартовой системы координат k = tg

α(0

≤

α

<

π)

(рис. 8).

Рисунок 8

Уравнение прямой с угловым коэффициентом k имеет

вид

y=kx+b, (2)

где k ― угловой коэффициент, b=OB ― величина отрезка, от-

секаемого на оси Oy.

Если прямая задана уравнением (1), то ее угловой коэф-

фициент k определяется по формуле

.

B

A

k −= (3)

Уравнение прямой, проходящей через данную точку

М

0

(х

о

;y

0

), с угловым коэффициентом k имеет вид

y - y

0

= k(x - x

0

). (4)

Угловой коэффициент прямой, проходящей через точки

М

1

(х

1

;y

1

) и М

2

(х

2

;y

2

), определяется по формуле

.

12

xx

yy

k

−

=

(5)

Уравнение прямой, проходящей через две различные точ-

ки М

1

(х

1

;y

1

) и М

2

(х

2

;y

2

), имеет вид:

),(.

1212

12

1

12

1

yyxx

xx

yy

≠≠

−

=

−

. (6)

Пусть k

1

и k

2

― угловые коэффициенты двух прямых.

Тогда один из углов

ϕ

между ними определяется по формуле

12

1 kk

kk

tg

+

−

=

ϕ

. (7)

Если k

1

= k

2

, то прямые параллельны. Если k

1

k

2

= -1, то

прямые

перпендикулярны.

Уравнение вида

)0( 1 ≠+=+ ba

b

y

a

x

(8)

называется

уравнением прямой в отрезках.

Расстояние

d от точки М

0

(х

0

;y

0

) до прямой (1) вычисляет-

ся по формуле

.

22

00

BA

CByAx

d

+

++

=

(9)

6.1. Примеры решения типовых задач

Пример 1. Получить уравнение прямой, проходящей че-

рез точку М

1

(х

1

;y

1

) параллельно прямой Ax + By + C = 0.

49 50

Решение. Искомое уравнение имеет вид

()

11

xxkyy −=− .

Из параллельности прямых следует, что k = - A/B. Окон-

чательно получаем:

() ()()

0 ,0

1111

=−+−=−+− yyBxxAxx

B

A

yy .

Ответ: A(x - x

1

) + B(y - y

1

) = 0.

Пример 2. Даны уравнения основания равнобедренного

треугольника x+y+1=0 и боковой стороны x - 2y - 3 = 0. Соста-

вить уравнение третьей стороны треугольника, если известно,

что на ней лежит точка Р(-3;-1).

Решение. Преобразуем уравнения сторон к виду y = -x -

1,

y = x/2 - 3/2. Следовательно, данные прямые имеют угловые

коэффициенты k

1

= -1 и k

2

=1/2. По формуле (7) находим тан-

генс угла между ними:

.3

2

1

2

1

=

−

+

=

ϕ

tg

Уравнение третьей стороны ищем в виде y = kx + b. По

условию эта сторона образует с основанием x + y + 1 = 0 та-

кой же угол, что и данная сторона x - 2y - 3 = 0. Поэтому

tg

ϕ

=(k+1)/(1-k) или tg

ψ

= (-1-k)/(1-k) (в зависимости от того,

какую из двух рассматриваемых прямых считать первой). По-

лучаем уравнения:

,3

1

3

1

==

−

+

k-

k+

, -

k

откуда находим k=1/2, k=2. Берем второе значение k =2, так

как первое относится к заданной боковой стороне x-2y-3=0.

Уравнение искомой стороны принимает вид y=2x+b. Учиты-

вая, что искомая прямая проходит через точку Р(-3;-1), получа-

ем: -1=2(-3)+b, откуда b=5.

Ответ: y=2x+5.

Пример 3. Составить уравнения прямых, на которых ле-

жат стороны и высоты

треугольника с вершинами А(3;4),

В(6;2) и С(3;

2

1

).

Решение. Найдем уравнение прямой, на которой лежит

сторона АВ. Воспользуемся формулой (6). В нашем случае

имеем: x

1

=3, y

1

=4, x

2

=6, y

2

=2. Тогда формула (6) примет вид:

.

36

3

42

4

−

=

−

− xy

Отсюда имеем уравнение прямой, на которой ле-

жит сторона АВ : 2x+3y-18=0. Аналогично составляем уравне-

ние прямой, на которой лежит сторона ВС:

,

63

6

2

1

2

−

=

−

− xy

т.е. x-2y-2=0. Уравнение третьей стороны АС имеет вид:

.

33

3

4

2

1

4

−

=

−

− xy

Следовательно, x-3=0.

При составлении уравнений прямых, на которых лежит

высота треугольника, воспользуемся формулой (4) и условием

перпендикулярности прямых. Прямая АВ имеет угловой коэф-

фициент k

AB

=-

3

2

. Тогда высота к ней, проведенная из точки С,

имеет угловой коэффициент k=

2

3

. Используя формулу (4)

(здесь x

0

=

2

1

, y

0

=3), получаем уравнение высоты h

AB

:

3x-3y-8=0. Аналогично получаем уравнение прямой, на кото-

рой лежит высота треугольника h

BC

, проведенная из точки А:

51 52

2x+y-10=0. Так как прямая АС параллельна оси Оy, то высота

h

AC

, проведенная из точки В, параллельна оси Ох и имеет вид

y=2.

Ответ: 2x+3y-18=0 (AB); x-2y-2=0 (BC); x-3=0 (AC); 3x-

2y-8=0 (h

AB

); 2x+y-10=0 (h

BC

); y=2 (h

AC

).

Пример 4. Доказать, что уравнение прямой, проходящей

через две заданные точки М

1

(х

1

;у

1

) и М

2

(х

2

;у

2

), может быть за-

писано в виде

.0

1

22

11

=

yx

Доказательство. Уравнение прямой, проходящей через

две точки М

1

и М

2

, имеет вид:

.

12

1

12

1

xx

yy

−

=

−

Преобразуем его к виду

-x(y

2

-y

1

)+y(x

2

-x

1

)+x

1

y

2

- x

1

y

1

- y

1

x

2

+ x

1

y

1

=0

Ö

x(y

1

-y

2

)-y(x

1

-x

2

)+x

1

y

2

- y

1

x

2

=0.

Последнюю формулу представим в виде

.0

1

22

11

2

1

2

1

=+−

yx

x

y

x

Окончательно

.0

1

22

11

=

yx

Пример 5. Даны две смежные вершины А(-3;-1) и В(2;2)

параллелограмма АВСD и точка Q(3:0) пересечения его диаго-

налей. Составить уравнения сторон этого параллелограмма.

Решение. Пусть С(х

1

;у

1

), D(x

2

;y

2

) ― координаты неиз-

вестных

вершин. Тогда Q ― середина диагонали АС. Поэтому получа-

ем уравнения:

0.=

2

y+1-

3,=

2

3

11

x

+

−

Из них находим: С(х

1

;у

1

)

=

= С(9;1). Точка Q ― середина диагонали BD, поэтому

,0

2

,3

2

22

=

+

=

+ yx

откуда х

2

= 4, у

2

= -2, то есть, имеем

D(4;-2). Воспользовавшись формулой (6), находим искомые

уравнения сторон:

,

23

2

21

2

−−

−

=

−−

− xy

т.е. -3x+5y-4=0

уравнение стороны АВ

,

29

2

21

2

−

=

−

− xy

т.е. 7у+х-16=0

уравнение стороны ВС

,

94

9

12

1

−

=

−−

− xy

т.е. 5у-3х+22=0

уравнение стороны CD

,

34

3

12

1

+

=

+−

+ xy

т.е. 7у+х+10=0

уравнение стороны AD

Ответ: -3x+5y-4=0; 7у+х-16=0; 5у-3х+22=0; 7у+х+10=0.

Пример 6. Доказать, что прямая 2х-3у+6=0 не пересекает

отрезок, ограниченный точками М

1

(-2;-3) и М

2

(1;-2).

Решение. Найдем отклонение δ(М

0

) от точек М

0

(х

0

;у

0

) до

прямой Ах+Ву+С=0 по формуле

.)(

22

00

0

BA

CByAx

M

+

=

δ

Очевидно, что если δ(М

1

) и δ(М

2

) имеют одинаковый

знак, то они лежат по одну сторону от прямой L, то есть, пря-

мая L не проходит через отрезок М

1

М

2

. В нашем случае име-

ем:

53 54

.

13

14

13

212

13

6)2(312

)(

;

13

11

13

694

94

6)3(3)2(2

)(

2

1

=

+

=

+−⋅−⋅

=

++−

=

+

+−⋅−

−

⋅

=

M

δ

Так как δ(М

1

)>0 и δ(М

2

)>0, то отрезок М

1

М

2

лежит по

одну сторону от прямой, то есть, прямая L не проходит через

отрезок М

1

М

2

.

6.2. Задачи для самостоятельного решения

1. Составить уравнения прямых, параллельных биссектрисе

первого координатного угла и отсекающих на оси Оу отрезки,

величина которых равна соответственно b

1

=2, b

2

=-5.

2. Написать уравнения прямых, отсекающих на оси Оу отрезок

b=-3 и образующих с осью Ох углы ϕ

1

=0, ϕ

2

=45

0

, ϕ

3

=60

0

,

ϕ

4

=135

0

.

3. Найти углы, образуемые с осью Ох следующими прямыми:

1) 2х-2у+5=0; 2) 3х+3у-7=0; 3) 6х-3у-1=0; 4) 7х+10=0;

5) 3у+7=0; 6) 15х+5у-14=0.

4. Вычислить площадь треугольника, заключенного между

осями координат и прямой 4х+5у-20=0.

5. Найти углы между прямыми: 1) у=4х/3-2, y=x/7+3;

2) y=3x/5+1, y=4x-5; 3) y=

2

х

+6, x-2y-6=0; 4) y=

7

4х

-2,

7x+4y-10=0.

6. Стороны АВ, ВС и АС треугольника АВС заданы уравне-

ниями 4х+3у-5=0, х-3у+10=0, х-2=0. Определить координаты

его вершин.

7. Стороны треугольника лежат на прямых х+5у-7=0,

3х-2у-4=0, 7х+у+19=0. Вычислить его площадь S.

8. Даны уравнения двух сторон прямоугольника 2х-3у+5=0,

3х+2у-7=0 и одна из его вершин

А(2;-3). Составить уравнения

двух других сторон прямоугольника.

9. Вычислить угловой коэффициент k прямой, проходящей

через две данные точки:) М

1

(2;-5), М

2

(3;2); 2) Р(-3;1), Q(7;8);

3)А(5;-3), В(-1;6).

10. Составить уравнения прямых, проходящих через вершины

треугольника А(5;-4), В(-1;3), С(-3;-2) параллельно противопо-

ложным сторонам.

11.

Даны вершины треугольника М

1

(2;1), М

2

(-1;1) и М

3

(3;2).

Составить уравнения его высот.

12. Даны вершины треугольника А(1;-1), В(-2;1) и С(3;5). Со-

ставить уравнение перпендикуляра, опущенного из вершины А

на его медиану, проведенную из вершины В.

13.

Даны вершины треугольника А(2;-2), В(3;-5) и С(5;7). Со-

ставить уравнение перпендикуляра, опущенного из вершины С

на биссектрису внутреннего угла при вершине А.

14.

Точка А(-4;5) является вершиной квадрата, диагональ кото-

рого лежит на прямой 7х=у+8=0. Составить уравнения сторон

и второй диагонали квадрата.

15.

Даны две вершины треугольника М

1

(-10;2) и М

2

(6;4); его

высоты пересекаются в точке N(5;2). Определить координаты

третьей вершины М

3

.

16. Вычислить расстояние d точки от прямой в каждом из сле-

дующих случаев: 1) А(2;-1), 4х+3у+10=0; 2) В(0;-3),

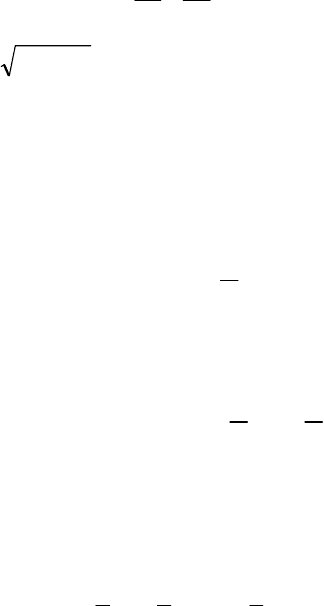
55 56

5х-12у-23=0; 3) Р(-2;3), 3х-4у-2=0; 4) Q(1;2), х-2у-5=0.

17. Точка А(2;5) является вершиной квадрата, одна из сторон

которого лежит на прямой х-2у-7=0. Вычислить площадь этого

квадрата.

18. Доказать, что прямая 2х+у+3=0 пересекает отрезок, огра-

ниченный точками А(-5;1) и В(3;7).

19. Доказать, что через точку Р(2;5) можно провести две пря-

мые так, что их расстояния от точки Q(1;2) равны 5. Составить

уравнения этих прямых.

7. КРИВЫЕ ВТОРОГО ПОРЯДКА НА ПЛОСКОСТИ.

ОКРУЖНОСТЬ. ЭЛЛИПС. ГИПЕРБОЛА. ПАРАБОЛА

Определение. Уравнение

(

)( )

2

22

Ryx =−+−

βα

(1)

определяет окружность радиуса R с центром в точке (α;β).

Если центр окружности совпадает с началом координат,

т.е. α= β=0, то уравнение (1) имеет вид

222

Ryx =+ .

Определение. Эллипсом называется геометрическое ме-

сто точек, для которых сумма расстояний до двух фиксирован-

ных точек плоскости, называемых фокусами, есть постоянная

величина, большая, чем расстояние между фокусами (рис. 9).

Постоянную сумму расстояний произвольной точки эл-

липса до фокусов принято обозначать через 2а. Фокусы эллип-

са обозначаются F

1

и F

2

; расстояние между ними ― через 2с.

Пусть М(х;у) ― произвольная точка эллипса. Тогда по условию

|

F

1

M

|

+

|

F

2

M

|

= 2a.

Если в прямоугольной декартовой системе координат

фокусы эллипса расположены в точках F

1

(-c;0), F

2

(c;0), то

уравнение эллипса имеет вид

,1

2

=+

b

y

a

x

(2)

где

22

cab −=

; очевидно, что а>b. Уравнение вида (2) на-

зывается

каноническим уравнением эллипса.

При указанном выборе системы координат оси координат

являются осями симметрии эллипса, а начало координат - его

центром симметрии. Точки, в которых эллипс пересекает свои

оси, называются его

вершинами.

Число

a

c

=

ε

(3)

где а ― большая полуось, называется

эксцентриситетом

эллипса. На большей оси расположены фокусы эллипса. Оче-

видно, что 0<

ε

<1 (для окружности

ε

=0). Прямые

,=y ,

εε

aa

x −=

(4)

где

ε

определятся формулой (3), и в формуле (2) а>b, называ-

ются

директрисами эллипса.

 Если b>a, то фокусы эллипса (2) расположены в точках

F1(0;-c), F2(0;c), а его директрисы определяются уравне-

ниями

. , где ,

b

= ,

222

abc

b

c

y

b

y −==−=

ε

 Пусть r ― расстояние произвольной точки М(х;у) до бли-

жайшего фокуса, d ― расстояние от этой же точки до

односторонней с фокусом директрисы. Тогда r/d есть по-

стоянная величина, равная эксцентриситету эллипса:

r/d=

ε

.

57 58

Рисунок 9

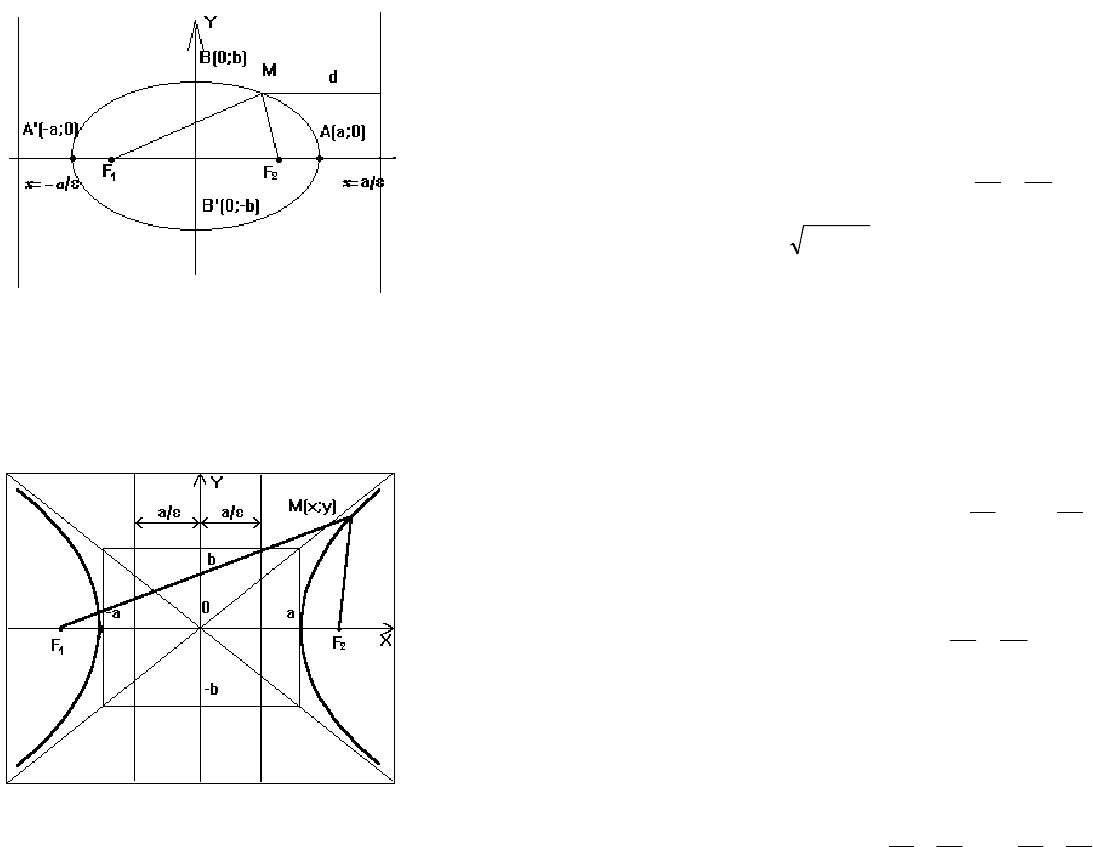
Определение. Гиперболой называется геометрическое ме-

сто точек, для которых модуль разности расстояний до двух

фиксированных точек F

1

и F

2

плоскости, называемых фоку-

сами, есть величина постоянная, меньшая расстояния между фоку-

сами (рис. 10).

Рисунок 10

Фокусы гиперболы обозначаются через F

1

и F

2

; расстоя-

ние между ними ― через 2с. По определению гиперболы

2а<2с. Пусть М(х;у) ― произвольная точка гиперболы. Тогда

по условию

|

F

1

M

|

-

|

F

2

M

|

= 2a. (5)

В прямоугольной декартовой системе координат поло-

жим F

1

(-c;0), F

2

(c;0). Тогда уравнение гиперболы (5) может

быть преобразовано к каноническому виду

,1

2

=−

b

y

a

x

(6)

где

22

acb −=

.

 Из уравнения (6) следует, что оси координат являются

осями симметрии гиперболы, а начало координат ―

ее

центром симметрии. Ось Ох, на которой располо-

жены фокусы гиперболы, называется действительной, а

ось

Oy называется мнимой осью.

Прямоугольник со сторонами

2а и 2b, расположенный

симметрично относительно осей гиперболы и касающийся ее в

вершинах, называется

основным прямоугольником гиперболы.

Прямые

a

bx

-y

a

bx

y == ,

(7)

являются асимптотами гиперболы (6).

Уравнение

,1

2

=+−

b

y

a

x

(8)

определяет гиперболу с фокусами на оси ординат F

1

(0;c),

F

2

(0;c), c

2

=b

2

-a

2

. В этом случае модуль разности расстояний от

произвольной точки гиперболы до фокусов равна 2b.

Две гиперболы, определяемые уравнениями

1 ,1

2

=+−=−

b

y

a

x

b

y

a

x

(9)

59 60

в одной и той же системе координат, называются сопряжен-

ными

.

Число

,

a

c

=

ε

(10)

где

а ― действительная полуось, называется эксцентрисите-

том

гиперболы.

Прямые

ε

a

x ±=

называются директрисами гиперболы

(6), а прямые

ε

b

y ±=

― директрисами гиперболы (8).

 Если r ― расстояние от произвольной точки гиперболы

М(х; у) до ближайшего фокуса, d ― расстояние от этой

же точки до односторонней с этим фокусом директри-

сы, то отношение

d

r

есть величина постоянная, равная

эксцентриситету гиперболы:

d

r

= ε.

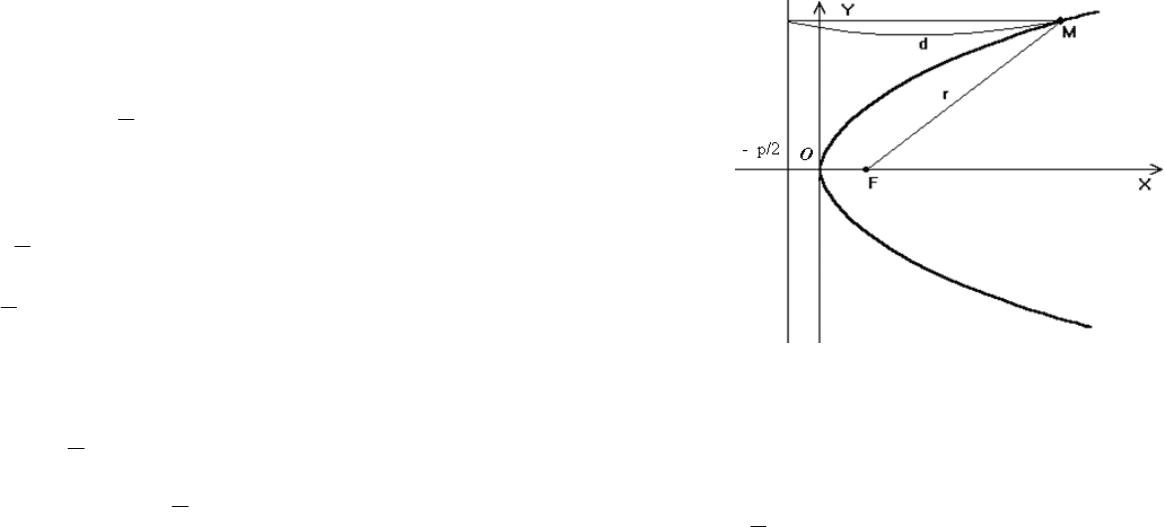
Определение. Параболой называется геометрическое

место точек, для каждой из которых расстояние до некоторой

фиксированной точки, называемой фокусом, равно расстоя-

нию до некоторой фиксированной прямой, называемой дирек-

трисой (рис. 11 а).

Фокус параболы обозначается буквой

F, а расстояние от

фокуса до директрисы ― через p. Число р называется пара-

метром параболы.

Рисунок 11 а

В прямоугольной декартовой системе координат, полагая

F(p/2;0), уравнение параболы преобразуется к каноническому

виду

у

2

= 2рх. (11)

В этой же системе координат уравнение директрисы име-

ет вид

х = -

2

p

.

Уравнения у

2

=-2рх, х

2

= 2рy, х

2

= -2рy (p>0) также опре-

деляют параболы, изображенные на рис. 11 б-11 г соответст-

венно.

Пчельник В.К. Пособие по курсу высшая математика. Матрицы и определители

Подождите немного. Документ загружается.