Пчельник В.К. Пособие по курсу высшая математика. Матрицы и определители
Подождите немного. Документ загружается.


81 82
Определение. Векторным произведением вектора
a
на
вектор
b
называется вектор, обозначаемый
ba×
и определяе-
мый тремя условиями:
1)
ϕ
sin⋅⋅=× baba
, где
ϕ
― угол между векторами
a
и
b
;
2) вектор ортогонален каждому из векторов
a
и
b
;
3) тройка векторов
a
,
b
,
ba×
является правой.
Векторное произведение зависит от порядка сомножи-
телей, то есть,
abba ×−=×
.
Модуль векторного произведения равен площади S па-
раллелограмма, построенного на векторах
a
и
b
:
Sba =⋅⋅
ϕ
sin .
Пусть Охуz ― правая декартовая система координат, и
векторы
a
,
b
заданы своими координатами
{}{}
222111
; ; , ; ; zyxbzyxa ==
.
Тогда
, ; ;
22
11
22
11
22
11
⎭
⎬
⎫
⎩
⎨
⎧
−=×
yx
yx
zx
zx
zy
zy
ba
или
.
222
111
zyx
zyx
kji
ba =×
Определение. Смешанным произведением трех векторов
, , cba
называется число, равное векторному произведению
ba ×
, умноженному скалярно на вектор
c
, то есть,
(
)
cbacba ⋅⋅=•×
Смешанное произведение
cba
равно объему паралле-
лепипеда, построенного на векторах
, , cba
, взятому со
знаком плюс, если тройка векторов
, , cba
правая, и со
знаком минус, если эта тройка левая.
Определение. Векторы
, , cba
называются компланар-
ными
, если они лежат в параллельных плоскостях.
Необходимым и достаточным условием компланарно-
сти трех векторов
, , cba
является выполнение равен-
ства
0 =cba
.
Если векторы
, , cba
заданы своими координатами в
правой системе координат Охуz
{}{}{}
, ; ; , ; ;, ; ;
333222111
zyxc zyxb zyxa ===
то смешанное произведение определяется формулой
.
333
222
111
zyx
zyx
zyx
cba =
8.1. Примеры решения типовых задач
Пример 1. Определить конец вектора
a
={α; β; γ}, если
его начало совпадает с точкой М
0
(х
0
; у
0
; z
0
).
Решение. Пусть точка М(х; у; z) - конец вектора. Тогда
MM
0
=
a
={α; β; γ} ==x-x
0
; y-y
0
; z-z
0
}. Отсюда x-x
0
= α,
y-y
0
= β, z-z
0
= γ. Окончательно получаем: x = x
0
+ α, y = y
0
+
β, z = z
0
+ γ.
Ответ: x = x
0
+ α; y = y
0
+ β; z = z
0
+ γ.

83 84
Пример 2. Даны две координаты трехмерного вектора
х=5, z=10. Определить третью координату у при условии, что
|
a
| = 15.
Решение. Пусть
a
= {5; y; 10}. По условию |
a
|
=
y
2
125+ . Следовательно, у
2
= 225 - 125, у
2
= 100, у = ± 10.
Ответ: у = ± 10.
Пример 3. Может ли вектор
a
составлять с двумя коор-
динатными осями следующие углы: 1)
α = 60
0
, β = 30
0
; 2) β = 60
0
,
γ = 30
0
?
Решение. Пусть α, β, γ ― углы вектора
a
с координат-
ными осями. Тогда они удовлетворяют условию
cos
2
α + cos
2
β + cos
2
γ = 1. (*)
Находим: 1) cos
α = cos45
0
=
2
2
, cosβ = cos30
0
=
3
2
. Тогда
cos
2
45
0
+ cos
2
30
0
=1/2 + 3/4 = 5/4 > 1, что противоречит усло-
вию (*). Значит, вектор
a
не может составлять с координат-
ными осями данные углы.
2) cos
α = cos60
0
=
2
1
, cosγ = cos30
0
=
3
2
. Тогда cos
2
60
0
+
+ cos
2
30
0
=
.1
4
3
4
1
=+
Для угла β получим уравнение
cos
2
β= 0, то есть β = 90
0
.
Ответ: 1) не может; 2) может.
Пример 4. Начало вектора находится в точке М(4; -3; 5),
конец ― в точке N(6; -2; 3). Найти координаты вектора
MN
,
его длину и направляющие
косинусы.
Решение. Пусть вектор имеет координаты
MN
={x; y; z}.
По формулам x = х
2
- х
1
, y=у
2
- у
1
, z=z
2
- z
1
находим: x=6-4=2,
y=-2-(-3)=1, z = 3 - 5 = -2, то есть
MN
= {2: 1; -2}. Далее,
|
MN
| = 39414
222
==++=++ zyx .
Находим направляющие косинусы:
.
3
2
cos ,
3
1
cos ,
3
2
cos −======
MN
z
MN
y
MN
x
γβα
Ответ
:
{}
.
3
2
cos ,
3
1
cos ,
3
2
cos ;3;2 ;1 ;2 −====−=
γβα
MNMN
Пример 5.
Даны векторы
a
= {1; 1; -1},
b
= {2; -1; 3},
c = [1; -2; 1}. Разложить вектор
d
= {12; -9; 11} по векто-
рам
a
,
b
, c .
Решение. Пусть
cbad
γβα
++=
, где α, β, γ - некото-
рые коэффициенты. Так как равные векторы имеют равные
коэффициенты, и координаты линейной комбинации векторов
равны соответствующим линейным комбинациям координат,
то
⎪
⎭
⎪
⎬
⎫
++−=
−−=−
++=
.311
,29
,212
γβα
γβα
γβα
Решив эту систему уравнений, найдем:
α = 2, β = 3, γ = 4.
Ответ:
cbad 432 ++=
.
Пример 6
. В треугольнике АВС проведена медиана АА
1
.
Выразить вектор
AA
1
через векторы
cBAaBC == ,
.
Решение
. Имеем:
.2/
11
acBAABAA +−=+=

85 86
Ответ:
.
2
11
a
cBAABAA +−=+=
Пример 7.
Векторы
a
,
b
, c взаимно перпендикулярны и
имеют общее начало Найти
|
a
+
b
+
c
|, если |
a
| = 10, |
b
| =
=
11, | c | = 2.
Решение. Вектор |
a
+
b
+ c | представляет собой диаго-
наль прямоугольного параллелепипеда, построенного на
векторах
cba , ,
. Тогда
.152254121100
222
==++=++=++ cbacba
Ответ
:
cba ++
=15.
Пример 8. Проверить, является ли четырехугольник с
вершинами в точках А(1; 1; 1), В(4; 4; 1), С(7; 1; 1), D(4; -2; 1)
квадратом.
Решение. Находим координаты векторов: }0 ;3 ;3{=AB ,
}.6 ;3 ;3{ },0 ;0 ;6{ −== ADAC
Если векторы
ADBCAB , ,
компланарны, то точки А, В,
С и D лежат в одной плоскости. Имеем:
.0
03
03
6
033
006
033
=
−
−=
−
Следовательно, точки А, В, С и D лежат в одной плоско-
сти. Если
ADCDBCAB ===
и ADAB
⊥
, то плоская фигура
АВСD является квадратом. В нашем случае векторы имеют
координаты
{
}
{
}
{
} {}
.9 ;3 ;3 ,6 ;3 ;3 ,0 ;3 ;3 ,0 ;3 ;3 −=−−=−== ADCDBCAB
Следовательно,
18==== ADCDBCAB
. Находим
.09900)3(333 =−=⋅+−⋅+⋅=• ADAB
Значит, АВСD является квадратом.
Пример 9. Найти внутренние углы треугольника с вер-
шинами А(1; 7; 2), В(5; -3; 3), С(12; -1; -5).
Решение
. Найдем угол α при вершине А. Находим
AB
= {4; -10; 1},
AC
={11; -8; -7}. Тогда
.
42
2
arccos,
2
2
234117
117
4964121110016
78044
cos
π
α
α
===
⋅
=
=
++⋅++
−+
=
⋅
•
=
ACAB
ACAB
.
Аналогично находим угол
β при вершине В:
B
A
={-4; 10; -1}, BC ={7; 2; -8}. Тогда
.
2
0arccos ,0
117117
0
64449110016
82028
cos
π
β
β
===
⋅
=
=
++⋅++
++−
=
⋅
•
=
BCBA
BCBA
Так как сумма всех внутренних углов треугольника равна
π, то угол γ при вершине С равен
.
442
π
π
π
πβαπγ
=−−=−−=
Ответ: ∠А = π/4; ∠В = π/2; ∠С = π/4.
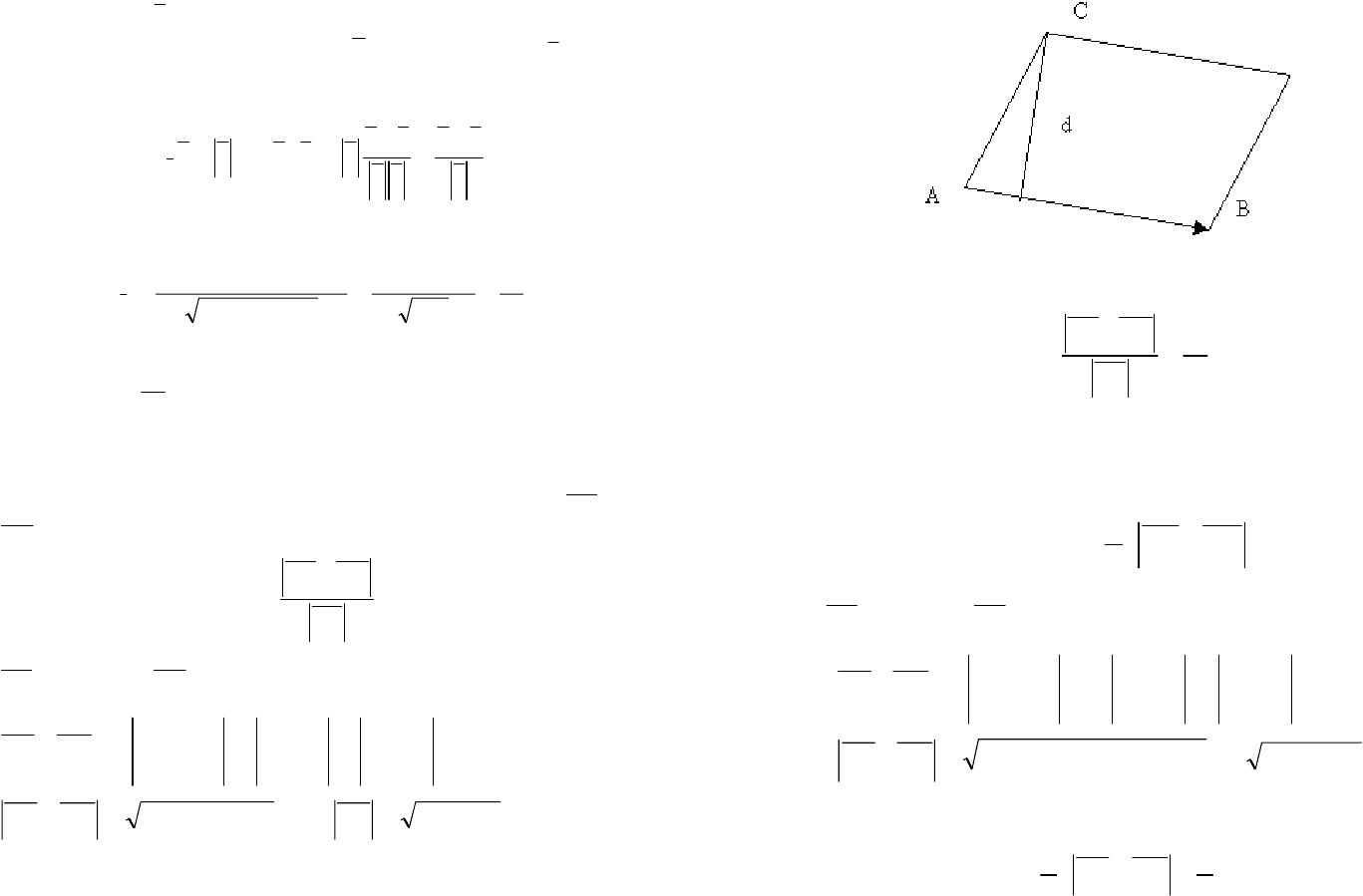
Пример 10. Вычислить проекцию вектора
a
= {1; -2; 2}
87 88
на ось вектора
b
= {2; 10; 11}.
Решение. Проекцию вектора
a
на ось вектора
b
нахо-
дим по формуле:
Пр
()
.^cos
b
ba
ba
ba
abaaa
b
•
=
•
==
В нашем случае имеем:
Пр
.
15
4
225
22202
1211004
11210)2(21
=
+−
=
++
⋅+⋅−+⋅
⋅=
b
Ответ:
.
15
4
Пример 11. Найти расстояние от точки С(4; -1; 2) до
прямой, проходящей через точки А(1; 3; 4) и В(3; 4; 2).
Решение. Построим параллелограмм на векторах AB и
AC (рис. 18). Тогда искомое расстояние d найдем по формуле:
.
AB
ACAB
d
×
=
В нашем случае последовательно находим:
AB
={2; 1; -2},
AC
={3; -4; -2};
{}
.3414 ;151214100
;11 ;2 ;10
43
12
;
23
22
;
24
21
=++==++=×
−−−=
⎭
⎬
⎫
⎩
⎨
⎧
−−
−
−−
−
=×
ABACAB
ACAB
Рисунок 18
Окончательно получаем:
.5
3
15
==
×
=
AB
ACAB
d
Ответ
: 5.
Пример 12. Вычислить площадь треугольника с верши-
нами А(1; 1; 3), В(3; -1; 6), С(5; 1; -3).
Решение. Воспользуемся формулой
.
2
1
ACABS
ABC
×⋅=
В нашем случае последовательно находим:
AB
={2; 2; 3},
AC
= {4; 0; -6};
{}
.2843694246434
,8 ;24 ;12
04
22
;
64
32
;
60
32
222222
=++=⋅+⋅+⋅=×
=
⎭
⎬
⎫
⎩
⎨
⎧
−
−
−
−
−
=×
ACAB
ACAB
Окончательно имеем:
.1428
2
1
2
1
=⋅=×⋅= ACABS
ABC
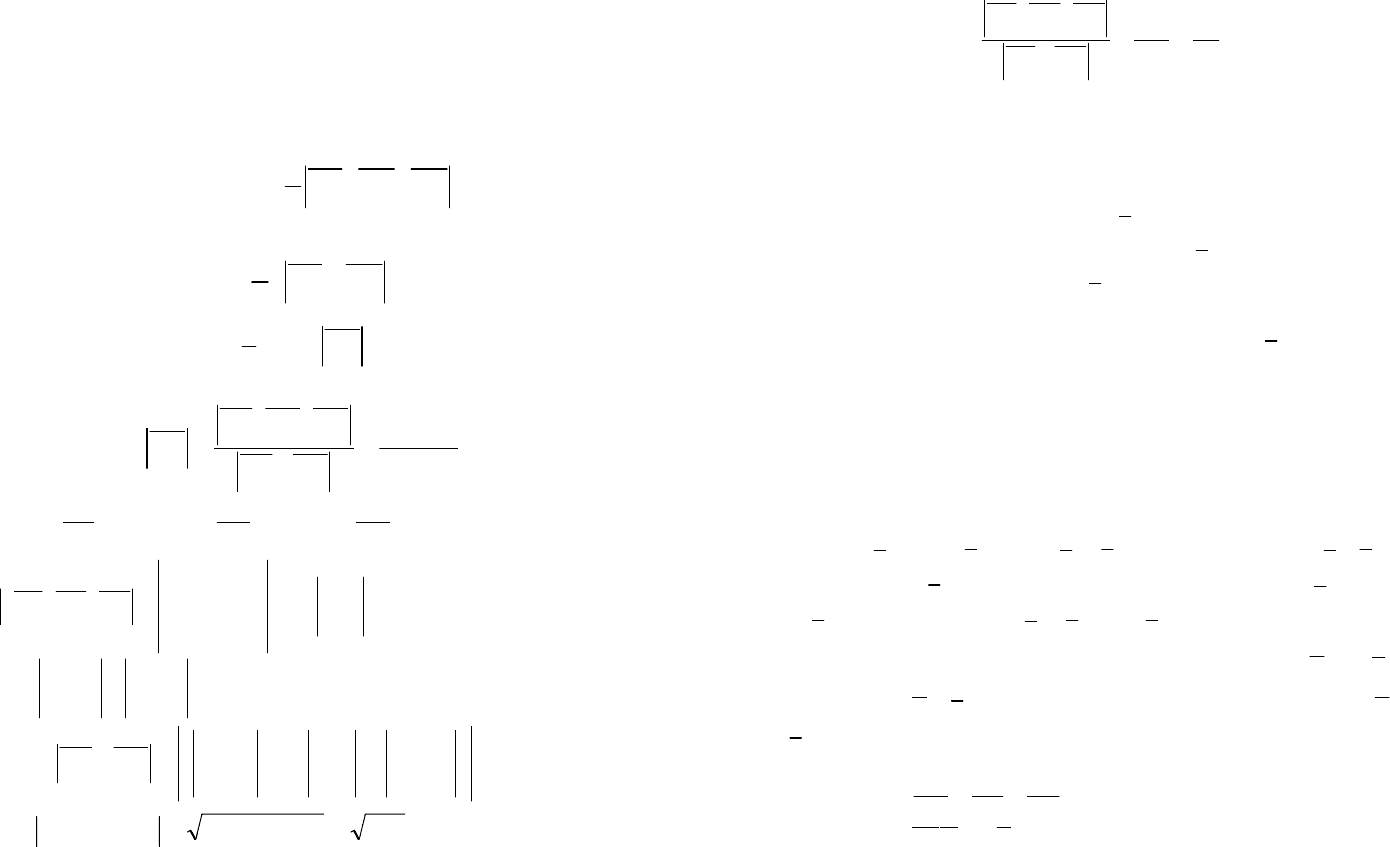
89 90
Ответ: 14 кв. ед.
Пример 13. Вершины треугольной пирамиды находятся в
точках А(2; 1; 1), B(6; -2; 2), С(4; 3; 2), D(-6; 8; 7). Вычислить
длину ее высоты, проведенной из вершины D.
Решение. Объем пирамиды АВСD найдем с помощью
смешанного произведения:
.
6
1
ADACABV ⋅⋅=
Площадь
грани АВС найдем по формуле
.
2
1
ACABS
ABC
×⋅=
C другой стороны,
,
3
1
DFSV
ABC
⋅=
где DF ― высота,
проведенная к грани АВС из точки D. Поэтому
.
2
6
ABC
S
V
ACAB
ADACAB
DFH
⋅
⋅
=
×
⋅⋅
==
В нашем случае последовательно находим:
};6 ;7 ;8{ },1 ;2 ;2{ },1 ;3 ;4{ −==−= ADACAB
+⋅=
−
−
=⋅⋅
67
12
4
678
122
134
ADACAB
;1103020354
78
22
68
12
3 =+⋅+⋅=
−
+
−
⋅+
{}
.1522519042514 ;2 ;5
22
34
;
12
14
;
12
13
==++=−−=
=
⎭
⎬
⎫
⎩
⎨
⎧
−
−
−
=×= ACABS
Окончательно получаем:
.
3
22
15
110
==
×
⋅⋅
=
ACAB
ADACAB
H
Ответ: 22/3.
8.2. Задачи для самостоятельного решения
1. Даны две координаты вектора
a
: х=4, у=-12. Определить
его третью координату
z при условии, что |
a
| = 13.
2.
Определить начало вектора
a
= {2; -3; -1}, если его конец
совпадает с точкой (1; -1; 2).
3.
Вычислить направляющие косинусы вектора
a
= {12; -15;
-16}.
4.
Может ли вектор составлять с координатными осями сле-
дующие углы 1)
α=45
0
, β=60
0
, γ=120
0
; 2) α=45
0
, β=135
0
, γ=60
0
;
3)
α=90
0
, β=150
0
, γ=60
0
?
5.
Может ли вектор составлять с двумя координатными осями
следующие углы: 1)
α=30
0
, β=45
0
; 2) α=60
0
, β=60
0
; 3) α=150
0
,
β=30
0
?
6.
Дано: |
a
| = 13, |
b
| = 19, |
a
+
b
| = 24 . Вычислить |
a
-
b
|.
7.
Векторы и
b
взаимно перпендикулярны, причем |
a
| = 5,
8.
|
b
| = 12. Определить |
a
+
b
| и | -
b
|.
9.
Какому условию должны удовлетворять векторы
a
и
b
,
чтобы вектор
a
+
b
делил пополам угол между векторами
a
и
b
?
10.
Точка О является центром тяжести треугольника АВС.
Доказать, что
OA OB OC
+
+
=
0.
11.
Три силы NM , и
P
, приложенные к одной точке, имеют
взаимно перпендикулярные направления. Определить величи-
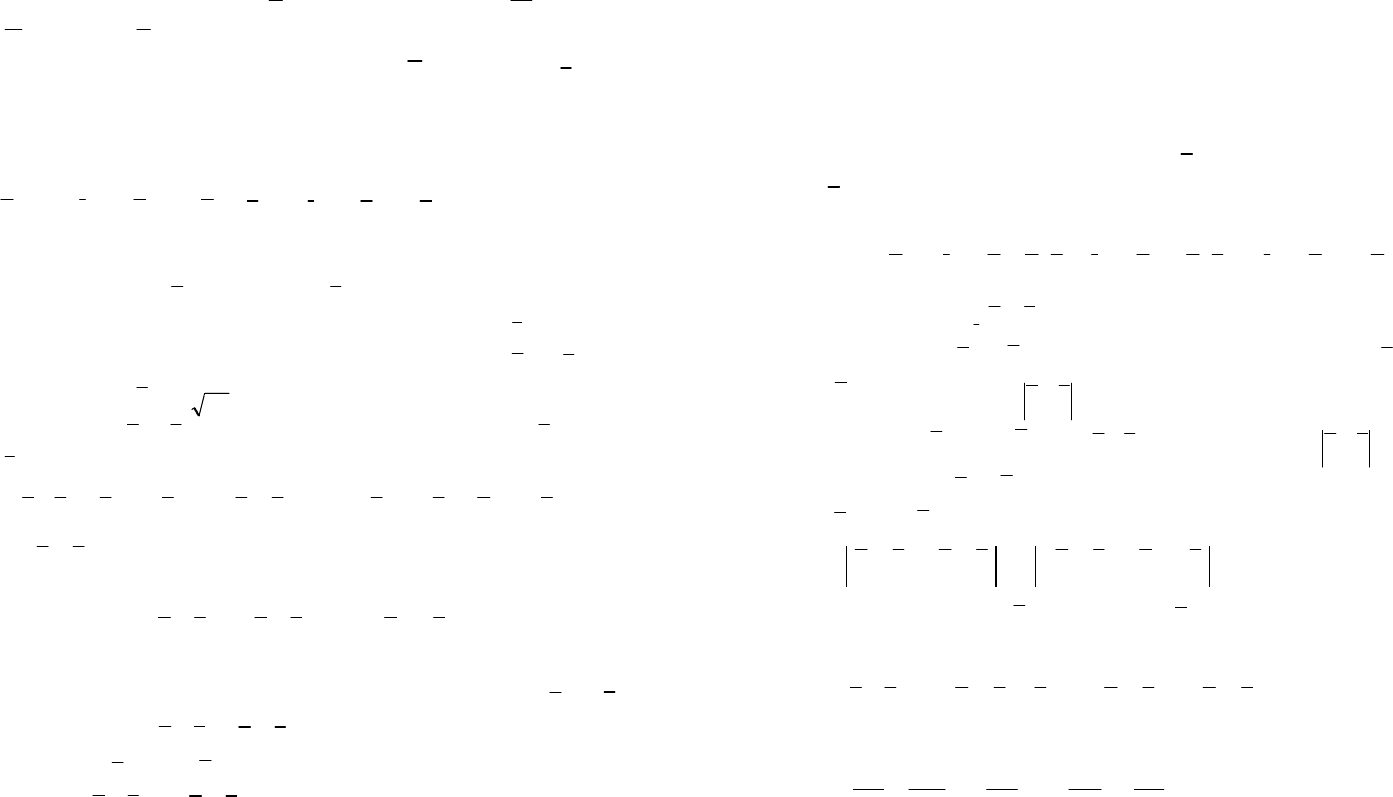
91 92
ну их равнодействующей
R
, если известно, что |
M
| = 2 кГ,
|
N
|= =10 кГ, |
P
| = 11 кГ.
12.
Проверить коллинеарность векторов
a
={22;-1;3} и
b
={-6;
3; -9}. Установить, какой из них длиннее другого и во сколько
раз; как они направлены ― в одну или в противоположные
стороны.
13.
Определить, при каких значениях α и β векторы
kjia ⋅+⋅+⋅−=
β
32
и
kjib ⋅+⋅−⋅= 262
коллинеарны.
14.
Проверить, что четыре точки А(3; -1; 2), В(1; 2; -1),
С(-1; 1;-3), D(3; -5; 3) служат вершинами трапеции.
15.
Два вектора
6} 3;- ;2{=a
и
2}- 2; ;1{−=b
приложены к
одной точке. Определить координаты вектора
c , направ-
ленного по биссектрисе угла между векторами
a
и b при
условии, что |
c
| = 423 .
16. Векторы
a
и b образуют угол ϕ = 2π/3. Зная, что |
a
| = 3,
|
b
| = 4, вычислить:
(
) ()
(
)
()
.a. 6)
;22a3 5) ;a 4) ; 3) ; a2) ;a )1
2
222
b
babbbb
−
⋅+•⋅−⋅+•
17.
Доказать справедливость тождества
(
) ()
⎟
⎠
⎞
⎜
⎝
⎛
+⋅=−++
2222
2 bababa
и выяснить его геометрический смысл.
18.
Какому условию должны удовлетворять векторы
a
и
b
,
чтобы векторы
ba +
и
ba −
были перпендикулярны?
19.
Дано: |
a
| = 3, |
b
| = 5. Определить, при каком значении α
векторы
ba +
и
ba −
будут взаимно перпендикулярны.
20.
Вычислить угол, образованный медианами, проведенными
из острых углов равнобедренного прямоугольного треугольни-
ка.
21.
Даны вершины четырехугольника А(1; -2; 2), В(1; 4; 0),
С(-4; 1; 1) и D(-5; -5; 3). Доказать, что его диагонали АС и ВD
взаимно перпендикулярны.
22.
Вычислив внутренние углы треугольника А(1; 2; 1),
В(3; -1 ;7), С(7; 4; -2), убедиться, что этот треугольник равно-
бедренный.
23.
Вычислить проекцию вектора
a
={5; 2; 5} на ось вектора
b
= {2; -1; 2}.
24.
Даны три вектора
.1243 ,34 ,63 kjickjibkjia +−=−+=−−=
Вычислить
(
)
.baÏð
ñ
+
25. Векторы
a
и
b
образуют угол ϕ = π/6. Зная, что |
a
| = 6,
|
b
| = 5, вычислить .ba ×
26.
Дано: |
a
| = 3, |
b
| = 2,
.12=• ba
Вычислить .ba ×
27. Векторы
a
и
b
взаимно перпендикулярны. Зная, что
|
a
| = 3, |
b
| = 4, вычислить:
()
(
)
(
)
(
)
.23 2) ;)1 babababa −×−−×+
28. Даны векторы
a
= {3; -1; -2},
b
= {1; 2; -1}. Найти коор-
динаты векторных произведений:
(
)
(
)
(
)
.22 3) ;2 2) ;a )1 bababbab +×−×+×
29.
Даны точки А(2; -1; 2), В(1; 2; -1) и С(3; 2; 1). Найти коор-
динаты векторных произведений:
(
)
12); . AB 2) BC×−⋅×BC CA CB
30.
Даны точки А(1; 2; 0), В(3; 0; -3), С(5; 2; 6). Вычислить пло-
щадь треугольника АВС.
31.
Даны вершины треугольника А(1; -1; 2), В(5; -6; 2),
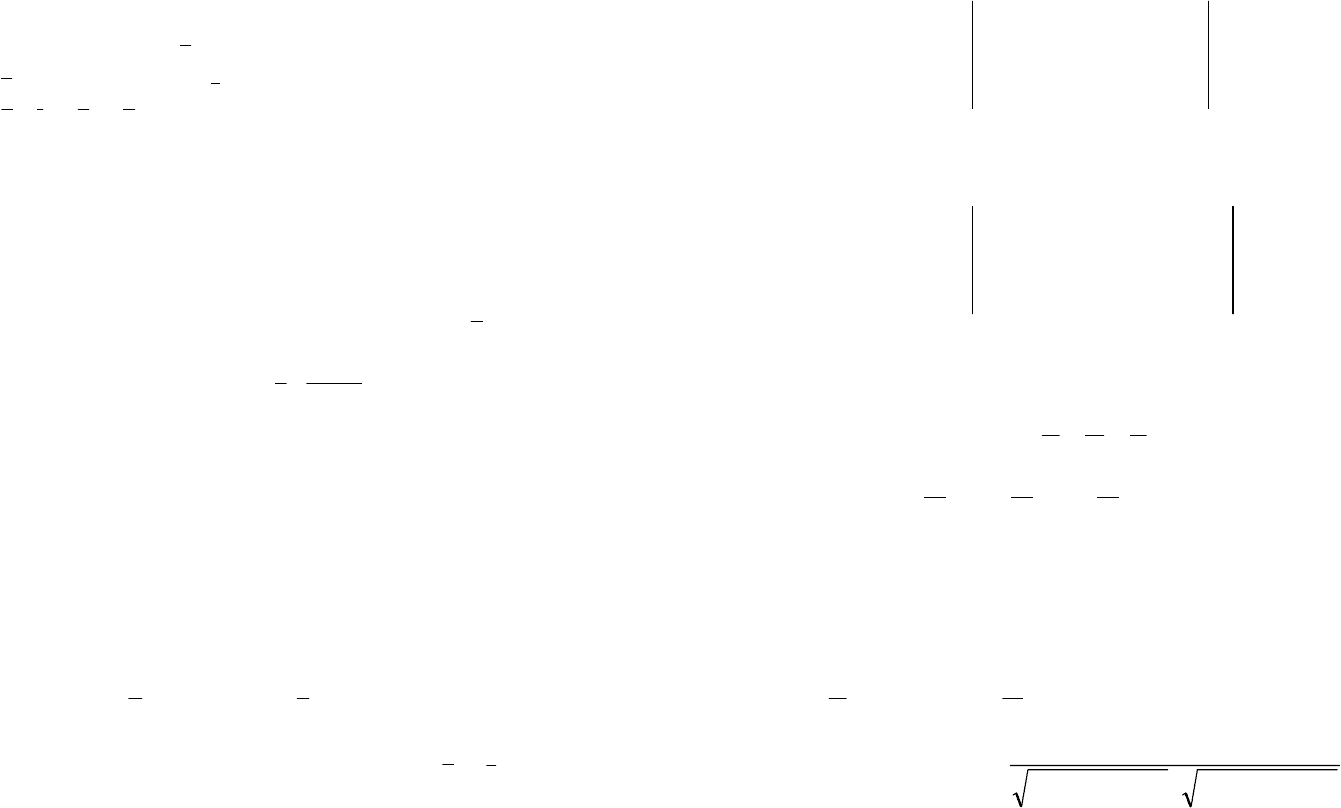
93 94
С(1; 3; -1). Вычислить длину его высоты, опущенной из вер-
шины В на сторону АС.
32.
Найти вектор
x
, зная, что он перпендикулярен к векторам
a
= {2; -3; 1} и
b
={1; -2; 3} и удовлетворяет условию
(
)
.1072 =−+• kjix
9. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
Определение. Нормальным вектором плоскости назы-
вается любой вектор, отличный от нулевого, перпендикуляр-
ный к этой плоскости.
Уравнение плоскости, проходящей через точку
М
0
(х
0
; у
0
; z
0
) и имеющей нормальный вектор
{
}
nABC= ;; , в
векторном виде записывается так:
,0
0
=• MMn
где М(х; у; z) ― произвольная точка искомой плоскости.
В декартовых координатах последнее уравнение имеет
вид:
А(х-х
0
) + В(у-у
0
) + С(z-z
0
) = 0, (1)
или
Aх + Ву +Сz + D = 0, (2)
где D = - Ах
0
- Ву
0
- Сz
0
.
Определение. Уравнение (2) называется общим уравне-
нием плоскости
, если А
2
+В
2
+С
2
≠0.
Пусть
{
} {}
321321
; ; , ; ; bbbbaaaa ==
― два неколли-
неарных вектора. Тогда уравнение плоскости, проходящей че-
рез точку М
0
(х
0
;у
0
;z
0
) параллельно векторам
a
и b , имеет вид
.0
321
321
000
=
−−−
bbb
aaa
zzyyxx
(3)
Уравнение плоскости, проходящей через три точки
М
1
(х
1
; у
1
; z
1
), М
2
(х
2
; у
2
; z
2
), М
3
(х
3
; у
3
; z
3
), имеет вид
,0
131313
121212
111
=
−−−
−−−
−−−
zzyyxx
zzyyxx
zzyyxx
(4)
где М(х; у; z) ― произвольная точка искомой плоскости.
Если все коэффициенты уравнения (2) отличны от нуля,
то его можно преобразовать к виду
,1=++
c
z
b
y
a
x
(5)
где
C
D
B
D
b
A
D
a
−=−=−= c , , ― величины направленных от-
резков, отсекаемых на осях координат. Уравнение (5) называ-
ется
уравнением плоскости в отрезках.
Угол между двумя плоскостями
A
1
x + B
1
y + C
1
z+D
1
=0, (6)
A
2
x + B
2
y + C
2
z+D
2
=0 (7)
определяется как угол между их нормальными векторами
{
}
1111
; ; CBAn = и
{
}
2222
; ; CBAn = по формуле
.cos
2
2
2
2
2
2
2
1
2
1
2
1
212121
CBACBA
CCBBAA
++⋅++
+
+
=
ϕ
Необходимое и достаточное условие перпендикулярно-
сти плоскостей (6) и (7) (их нормальных векторов

95 96
{}
1111
; ; CBAn = и
{
}
2222
; ; CBAn = ) имеет вид:
А
1
А
2
+ В
1
В
2
+ С
1
С
2
= 0. (8)
Необходимое и достаточное условие параллельности
плоскостей (6) и (7) имеет вид:
А
2
=
λ
А
1
, В
2
=
λ
В
1
,
С
2
=
λ
С
1
,
D
2
≠λ
D
1
, (9)
или
.
2
1
2
1
2
1
2
1
D
D
C
C
B
B
A
A
≠==
Необходимое и достаточное условие совпадения плоско-
стей (6) и (7) имеет вид:
А
2
=
λ
А
1
, В
2
=
λ
В
1
,
С
2
=
λ
С
1
,
D
2
=
λ
D
1
, (10)
или
.
2
1
2
1
2
1
2
1
D
D
C
C
B
B
A
A
===
Расстояние
d от точки М
0
(х
0
; у
0
; z
0
) до плоскости
Aх + Ву +Сz + D = 0 (А
2
+В
2
+С
2
≠0) вычисляется по формуле:
.
222
000
CBA
DCzByAx
d
++
+++
=
(11)
Определение. Направляющим вектором прямой назы-
вается любой ненулевой вектор, лежащий на данной прямой
или параллельной ей.
Параметрические уравнения прямой, проходящей через
данную точку М
0
(х
0
;у
0
;z
0
) и имеющей направляющий вектор
{}
321
,, aaaa =
, имеют вид:
х=х
0
+а
1
t, y=y
0
+a
2
t, z=z
0
+a
3
t, (12)
где
t
∈
(-
∞
; +
∞
).
Исключая параметр
t из уравнений (12), получаем кано-
нические уравнения прямой:
.
3
0
2
0
1
0
a
zz
a
yy
a
xx −
=
−
=
−
(13)
Уравнения прямой, проходящей через две точки
М
1
(х
1
; у
1
; z
1
) и М
2
(х
2
; у
2
; z
2
), имеют вид:
.
12
0
12
0
12
0
zz
zz
yy
yy
xx
xx
−
−
=
−
−
=
−
−
Угол
ϕ между двумя прямыми
х=х
1
+а
1
t, y=y
1
+a
2
t, z=z
1
+a
3
t, (14)
х=х
2
+а
1
t, y=y
2
+a
2
t, z=z
2
+a
3
t (15)
определяется как угол между их направляющими векторами
{
}
321
, , aaaa =
и
{
}
321
, , bbbb =
по формуле:
.cos
2
3
2
2
2
1
2
3
2
2
2
1
332211
bbbaaa
bababa
ba
ba
++⋅++
++
=
•
=
ϕ
(16)
Необходимое и достаточное условие перпендикулярно-
сти прямых (14) и (15) выражается равенством:
.0
332211
=++=• babababa
(17)
Расстояние d от точки М
0
(х
0
; у
0
; z
0
) до прямой (14) вы-
числяется по формуле
,
0
a
aMM
d
×
=
(18)
где
М
1
(х
1
; у
1
; z
1
) ― точка прямой (14), а
{
}
321
, , aaaa =
―
направляющий вектор этой прямой. В координатной форме
формула (18) имеет вид:
.
2
3
2
2
2
1
2
21
0101
2
32
0101
2
32
0101
aaa
aa
yyxx
aa
zzxx
aa
zzyy
d
++
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−
=
(19)
Расстояние
d между прямыми (14) и (15) определяется
формулой:
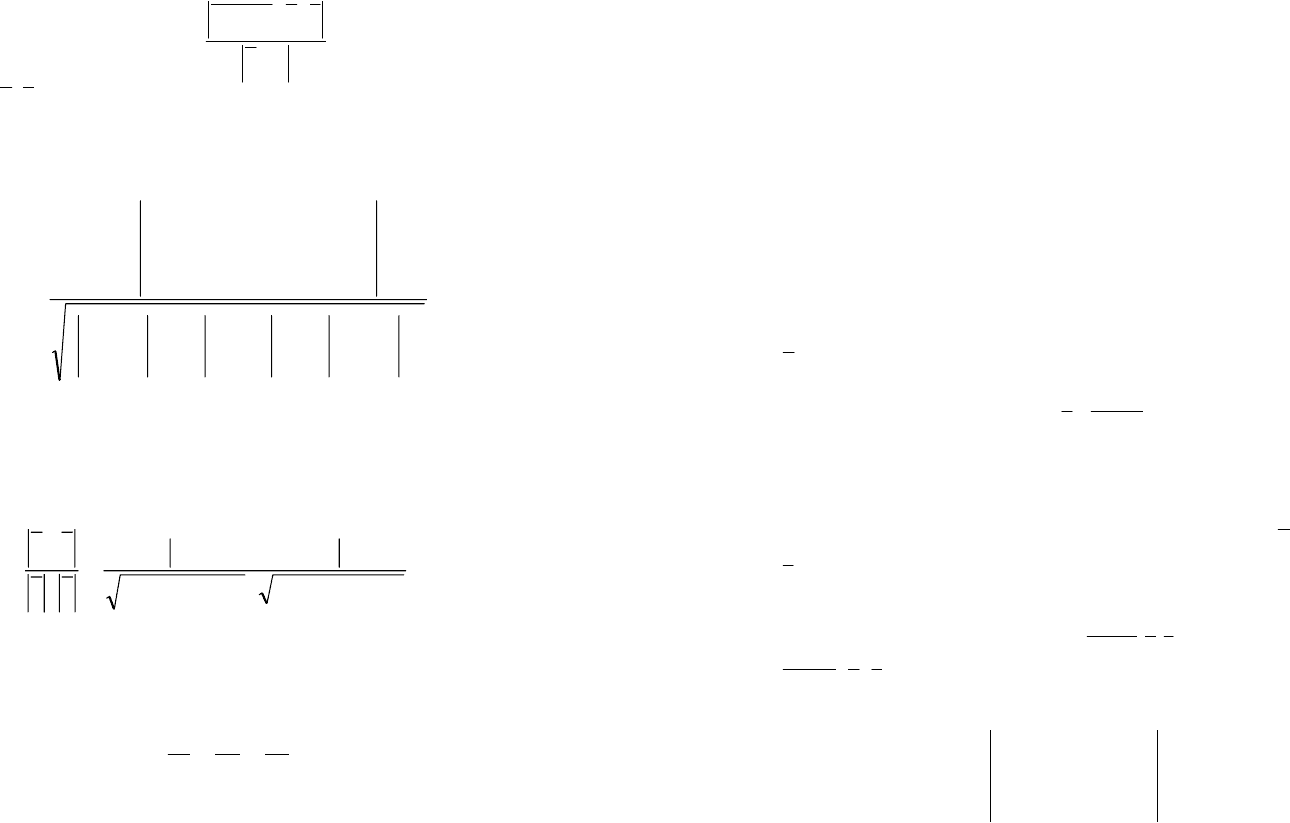
97 98
,
21
ba
baMM
d
×
⋅⋅
=
(20)
где
ba , ― направляющие векторы прямых (14) и (15), а
М
1
(х
1
; у
1
; z
1
), М
2
(х
2
; у
2
; z
2
), - точки, через которые проходят
прямые (14) и(15) соответственно.
В координатной форме формула (20) имеет вид:
.
mod
2
22
22
2
31
31
2
32
32
321
321
121212
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−−
=
bb
aa
bb
aa
bb
aa
bbb
aaa
zzyyxx
d
(21)
Угол ϕ между прямой
х=х
0
+а
1
t, y=y
0
+a
2
t, z=z
0
+a
3
t (22)
и плоскостью
Aх + Ву +Сz + D = 0 (23)
определяется по формуле:
.
a Ba Aa
sin
2222
31
2
2
2
1
321
CBAaaa
C
na
na
++⋅++
++
=
⋅
•
=
ϕ
(24)
Прямая (22) и плоскость (23) параллельны, если
Аа
1
+ Ва
2
+ Са
3
= 0; (25)
перпендикулярны, если
321
a
C
a
B
a
A
== . (26)
Прямая (22) лежит в плоскости (23), если выполняются
условия:
Аа
1
+ Ва
2
+ Са
3
= 0, Ах
0
+ Ву
0
+ Сz
0
+D= 0. (27)
Решив систему уравнений
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=+++
+=
+=
+=
,0
,
,
,
30
20
10
dCzByAx
tazz
tayy
taxx
найдем координаты точек пересечения прямой (22) и плоско-
сти (23).
9.1. Примеры решения типовых задач
Пример 1. Составить уравнение плоскости, проходящей
через точку М
0
(-3; 5; -8) и имеющей нормальный вектор
{}
3 ;2 ;1−=n .
Решение. Пусть М(х; у ;z) ― произвольная точка иско-
мой плоскости. Тогда
.0
0
=• MMn В нашем случае
(x+3)(-1)+(y-5)2+(z+8)3=0. Окончательно -x+2y+3z+11=0.
Ответ: -x+2y+3z+11=0.
Пример 2. Написать уравнение плоскости, проходящей
через точку
М
0
(1; -2; 3) параллельно векторам
{}
4 ;3 ;2=a
и
{}
8 ;5 ;3−=b
.
Решение. Пусть М(х; у; z) ― произвольная точка искомой
плоскости. Тогда векторы
baMM ,,
0
компланарны, т.е.
0
0
=⋅⋅ baMM
. В координатной форме последнее условие при-
мет вид:
.0
853
432
321
=
−
−+− zyx
Вычисляя определитель, получим уравнение плоскости:
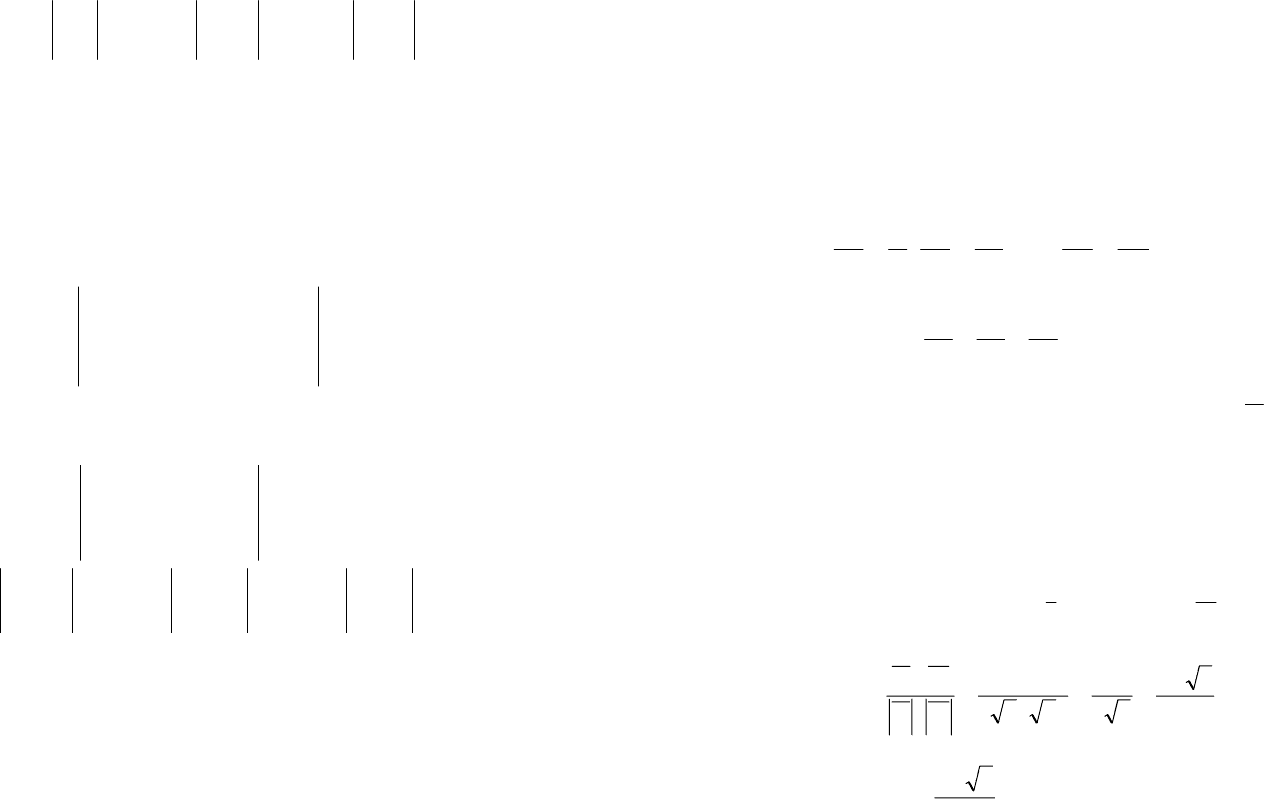
99 100
,0
53
32
)3(
83
42
)2(
85
43
)1( =
−
⋅−+
−
⋅+−⋅− zyx
011719284,019)3(28)2(4)1(
=
−
+
−=⋅
−
+
⋅
+−⋅− zyxzyx
Ответ
: 4x-28y+19z-117=0.
Пример 3. Написать уравнение плоскости, проходящей
через три данные точки
М
1
(5; 3; -2), М
2
(7; 6; 11), М
3
(-2; 2; -2).
Решение. Воспользовавшись уравнением плоскости, про-
ходящей через три данные точки,
,0
131313
121212
111
=
−−−
−−−
−−−
zzyyxx
zzyyxx
zzyyxx
в нашем случае получим:
,0
017
1332
235
=
−−
+−− zyx
.0254239113
,023)2(9)3(13)5(
,0
17
32
)2(
07
132
)3(
01
133
)5(
=++−
=⋅++⋅−−⋅−
=
−
⋅++
−
⋅−−
−
⋅−
zyx
zyx
zyx
Ответ: .0254239113 =+
+
−
zyx
Пример 4. Пересекает ли плоскость х + у - z + 15 = 0 от-
резок
М
1
М
2
, если М
1
(1; 1; 1), М
2
(-10; -7; 2)?
Решение. Обозначим
δ= + −
+
xyz15.
Находим
δδ () ,() .MM
12
11115 16 107 215 4=+
−
+
=
=
−
−
−
+
=
−
Так как
δ(M
1
)=16>0, δ(M
2
)-4<0, то точки М
1
и М
2
лежат
по разные стороны от заданной плоскости, то есть она пересе-
кает отрезок М
1
М
2
.
Ответ: пересекает.
Пример 5. Определить, при каких значениях параметра α
будут параллельны плоскости 2х + 3у + 9z + 15 = 0,
αх - у - 3z+ 7 = 0.
Решение. Находим:
.3
3
9
,3
1
3
,
2
2
1
2
1
2
1
−=
−
=−=
−
==
C
C
B
B
A
A
α
Если
,3
2
1
2
1
2
1
−===
C
C
B
B
A
A
то плоскости будут параллельны. Это возможно, если
2
α
=-3, то
есть,
α=-2/3.
Ответ: α=-2/3.
Пример 6.Найти угол между двумя плоскостями
х+у- z+3=0 и -2х-у+2z = 0.
Решение. Угол α между двумя плоскостями равен углу
между нормальными векторами
{
}
1:1:1
1
−=n и
{}
2;1;2
2
−−=n .
Тогда
.
9
35
33
5
93
212
cos
21
21
−
=
−
=
⋅
−−−
=
⋅
•
=
nn
nn
α
Ответ: α=arccos .
9
35−
Пример 7. Вычислить расстояние от точки М
1
(4; 2; -1) до
плоскости
10х + 11у -2z - 45 = 0.
