Панченков Г.М., Лебедев В.П. Химическая кинетика и катализ

Подождите немного. Документ загружается.

реакции.

Величина k в уравнении (64) описывается выражением

где

р —

плотность;

Af —

мольная масса твердого продукта реакции.

Второе уравнение Рогинского и Шульц относится к кинетике

реакции

в период снижения ее наблюдаемой скорости, Если счи-

тать, что на каждом кристаллике твердого реагента образовался

сплошной

слой твердого продукта и что скорость реакции по-

прежнему пропорциональна поверхности раздела фаз, сокращаю-

щейся

по мере

«сжатия»

реагента, т. е. по мере реакции, то для

кристалла сферической формы аналогично уравнению (64) можно

записать

dn/dt

k(a-

л)

2/3

(66)

где

а —

начальное количество твердого реагента;

п —

текущее количество

пре-

вращенного твердого реагента.

Уравнение (66) известно под названием «уравнение сжимаю-

щейся

сферы», хорошо передающим его физический смысл.

Чтобы перейти к более привычным обозначениям, проинтегри-

руем уравнение (66). Тогда получим

Разделив обе части равенства на а

'»; придем к выражению

(

)

l-(l

-x)

~k't

(68)

которое часто успешно применяется для описания кинетики реак-

ций

с участием твердых веществ на участке снижения скорости

реакции.

Широкая применимость этого уравнения связана с тем,

что такая же зависимость

будет

наблюдаться для кристалла лю-

бой формы, лишь бы эта форма не изменялась по мере роста слоя

продукта и

«сжатия»

исходного кристалла. При этом значение k

уравнениях (66) и (67) определяется выражением (65).

10. Определение удельных скоростей реакции

на

поверхности раздела фаз

Приведенные

выше формулы, хотя и включают

удельную

скорость

реакции,

но содержат, кроме того, ряд

других

констант, часть

которых мы условились считать эмпирическими. Между тем знать

удельные скорости реакции для кинетического анализа реакции

необходимо в первую очередь. Располагая значениями удельных

скоростей — стационарных величин дающими количественную ха-

рактеристику реакционной способности, можно в рамках клас-

сических приемов кинетического анализа расшифровать

инфор-

мацию о механизме реакции, сделать сравнительные оценки

реакционной

способности различных веществ и т. п. Иначе говоря,

переход на язык удельных скоростей реакции сразу же

дает

един-

278

ство подходов, методов и идей в классической кинетике химиче-

ских реакций и кинетике гетерогенных процессов.

Тем не менее кинетика гетерогенных реакций длительное вре-

мя

развивалась в направлении феноменологической теории, харак-

теристики влияния дисперсности исходного твердого тела, его

дефектности и т. п. Лишь в начале 60-х годов в работах А. Я. Ро-

зовского и Б. Дельмона было введено понятие удельной скорости

реакции

на поверхности раздела фаз, разработаны методы ее оп-

ределения из кинетических данных и

других

задач. Рассмотрим

простейшие методы определения удельной скорости реакции.

Как

отмечалось, приведенные формулы наблюдаемой скорости

реакции

включают наряду с удельной скоростью реакции два

эмпирических

параметра; для их исключения требуется дополни-

тельная информация, например еще одно уравнение. Естественно,

искать такое дополнительное уравнение в виде условия макси-

мума скорости реакции, тем более, что условия для особых точек

обычно содержат упрощенные зависимости, легко интерпретируе-

мые из экспериментальных данных.

В рамках допущения о независимом росте ядер фазы твердого

продукта максимальная скорость реакции должна наблюдаться

момент касания растущих ядер. Фактически касание и перекры-

вание части ядер начинается до момента максимума скорости ре-

акции.

Наряду с этим в момент максимума часть ядер

будет

еще

находиться на некотором расстоянии

друг

от

друга,

так что про-

цессы касания и перекрывания

будут

продолжаться и после мак-

симума скорости реакции. Влияние этих

двух

факторов элимини-

руется для величин степени превращения в момент максимума

времени максимума скорости реакции и, наоборот, складывается

для величины максимальной скорости реакции, приводя к умень-

шению

экспериментально наблюдаемого значения по сравнению

с рассчитанным по модели. Однако в тех

случаях,

когда это было

оценено

экспериментально, наблюдавшиеся отклонения в значениях

максимальной

скорости реакции были невелики и не превы-

шали 30%.

Исходя из проведенных рассуждений, введем допущение о том,

что в момент максимума скорости реакции поверхность твердого

реагента заполнена основаниями ядер фазы твердого продукта

(в

случае

изотропности исходного твердого тела — полусфер).

Будем считать, что эффективная площадь, занимаемая отдельным

ядром на исходной поверхности, равна площади квадрата, описан-

ного вокруг основания указанной полусферы. Тогда в момент ма-

ксимума скорости реакции

будем

иметь

(4/я)

ce4

(69)

где

S —

площадь исходной поверхности; S

—

суммарная площадь располо-

женных

на ней

оснований ядер.

Величина

сеч

может быть определена, например, интегрирова-

нием

уравнения, аналогичного основному уравнению (42), за-

писанного

для оснований ядер.- Соответствующие расчеты приво-

279

дят к выражениям для степенного закона образования ядер

2nM

a&$

t1-

fp*

(q - 1) (q - 2) (70)

для экспоненциальною закона

=)]

(71)

Из

полученных уравнений с

учетом

условия максимума ско-

рости реакции (69) и уравнений (54) и (56) можно определить

удельную

скорость реакции на поверхности раздела твердых фаз.

случае

степенного закона образования ядер

да

уа

2qn

M&KC

/ngSgt

M!UiC

(72)

где g и S

— масса и удельная поверхность исходного твердого тела соответ-

ственно.

случае

экспоненциального закона образования ядер фазы

твердого продукта получаем следующее выражение для удельной

скорости:

(Р'макс

— "макс)

(73)

Входящие в уравнения (72) и (73) коэффициенты (как и выбор

одного из них) определяют из экспериментальных кинетических

данных. Для этого нужно знать кинетику реакции в начальный

период (до максимума скорости) и параметры максимума /г

ма

кс

Гмакс

Другой способ определения удельной скорости реакции

следует

непосредственно из условия максимума (69). Действительно, для

ядер сферической формы площадь основания ядра равна половине

поверхности полусферы, которой пропорциональна наблюдаемая

скорость реакции. Это соображение

дает

простейший способ опре-

деления удельной скорости реакции

U№C

/ngS

(74)

Анализ показывает, что изменение формы ядер (кроме форм

типа иголок) мало влияет на погрешность определения удельной

скорости реакции, рассчитываемой по формуле (74). Если сущест-

венное

диффузионное торможение

отсутствует,

то можно считать,

что эта.формула

дает

нижний предел значения удельной скорости

реакции

с вероятным отклонением от действительного значения

до 30%.

Следует

также отметить, что после формирования сплошного

слоя

твердого продукта Wy

может также быть определена на

основании

уравнения «сжимающейся сферы», обсуждавшегося

выше.

Если это уравнение описывает экспериментальные данные,

то удельная скорость реакции может быть найдена из константы

уравнения по формуле (65). Этот путь, однако, менее надежен,

280

поскольку при значительных степенях превращения, когда при-

менимо

уравнение сжимающейся сферы, вероятность диффузион-

ного торможения (диффузия через слой твердого продукта) силь-

но

возрастает.

11.

Учет

перекрывания ядер в процессе роста

Рассмотрим решение задачи

учета

перекрывания ядер в про-

цессе роста для относительно простого случая, когда число ядер

ходе

реакции не изменяется. Будем полагать, что ядра распреде-

лены на исходной поверхности по закону случая, т. е. что их каса-

ние

можно рассматривать как случайный процесс, описывающийся

функцией

нормального распределения.

Тогда вероятность касания растущих ядер в момент времени т

определится выражением

w =

=^ ехр I - (т -

а)*/2о

1 (75;

где о и а — параметры распределения.

Суммарную реакционную поверхность (поверхность раздела

твердых фаз) можно выразить как

сумму

поверхности 5

независи-

мо растущих ядер, число которых равно JV

, и поверхности Si,

принадлежащей Ni взаимодействующим ядрам.

Для системы N ядер доля ядер, взаимодействующих в момент

т(т ^ f), составит

<jy2n

ехр [ - (т -

(76)

Для ядер сферической формы поверхность раздела 5,-

будет

равна

уд '

(

- йя -^

»lt-£j=

\ (t - х)

ехр [ - (т

-af/20

}

(77)

где А - среднее число ядер, с которым взаимодействует отдельное ядро.

Принимая

h =4, и учитывая, что N\ + #2 = Af, после интегри-

рования

выражения в правой части (77) получим

] ~ ехр ( -

У2

/ —а

ехр [ - (т — а)

где % =- 2я

(М/р)

w* JV

dx\

(78)

231

отсюда

w = xf - 2

/1-~- exp f - (/ -

а)

/2а

]

—=-

exp ( -

а'/2а

)

рг \ ехр I - (т - c)

2 J

dx (79)

где х=хЧд

Для проведения расчетов в уравнении (79) последний член может

быть выражен в виде

t — a f

—-=-

J exp [ - (т -

а)У2а

dj=>(t-

а) [Ф (a/a) + Ф K* -

a)/a]}

(80)

где Ф(х) —табличный интеграл Лапласа.

Пределы применимости уравнения (79)

соответствуют

преде-

лам применимости ядерной модели, что

соответствует

периоду

роста скорости, включая максимум, и часть периода снижения

скорости, пока ядра не сливаются в сплошной слой. .

Первый член правой части уравнения (79) выражает скорость

реакции при независимом росте ядер, а остальные —поправку на

перекрывание ядер. Для начального

участка

кинетической кривой

можно пренебречь всеми членами правой части уравнения, кроме

первого, что позволяет определять коэффициент при первом члене

«независимых»

изменениях. Такое определение целесообразно

проводить на первой ступени анализа экспериментальных данных.

Кроме константы % уравнение (79) включает параметры функ-

ции

распределения а и о. Эти параметры имеют следующий смысл.

Параметр а для данной задачи численно равен времени, при кото-

ром число касаний ядер в единицу времени максимально. В этом

легко убедиться, вернувшись к урав-

нению (75), правая часть которого

принимает максимальное значение при

т = а.

«Высота»

этого максимума об-

ратно пропорциональна значению па-

раметра а, который, таким образом,

характеризует

рассеяние случайной

величины вокруг ее математического

ожидания. Чем меньше значение па-

раметра а, тем большее число ядер

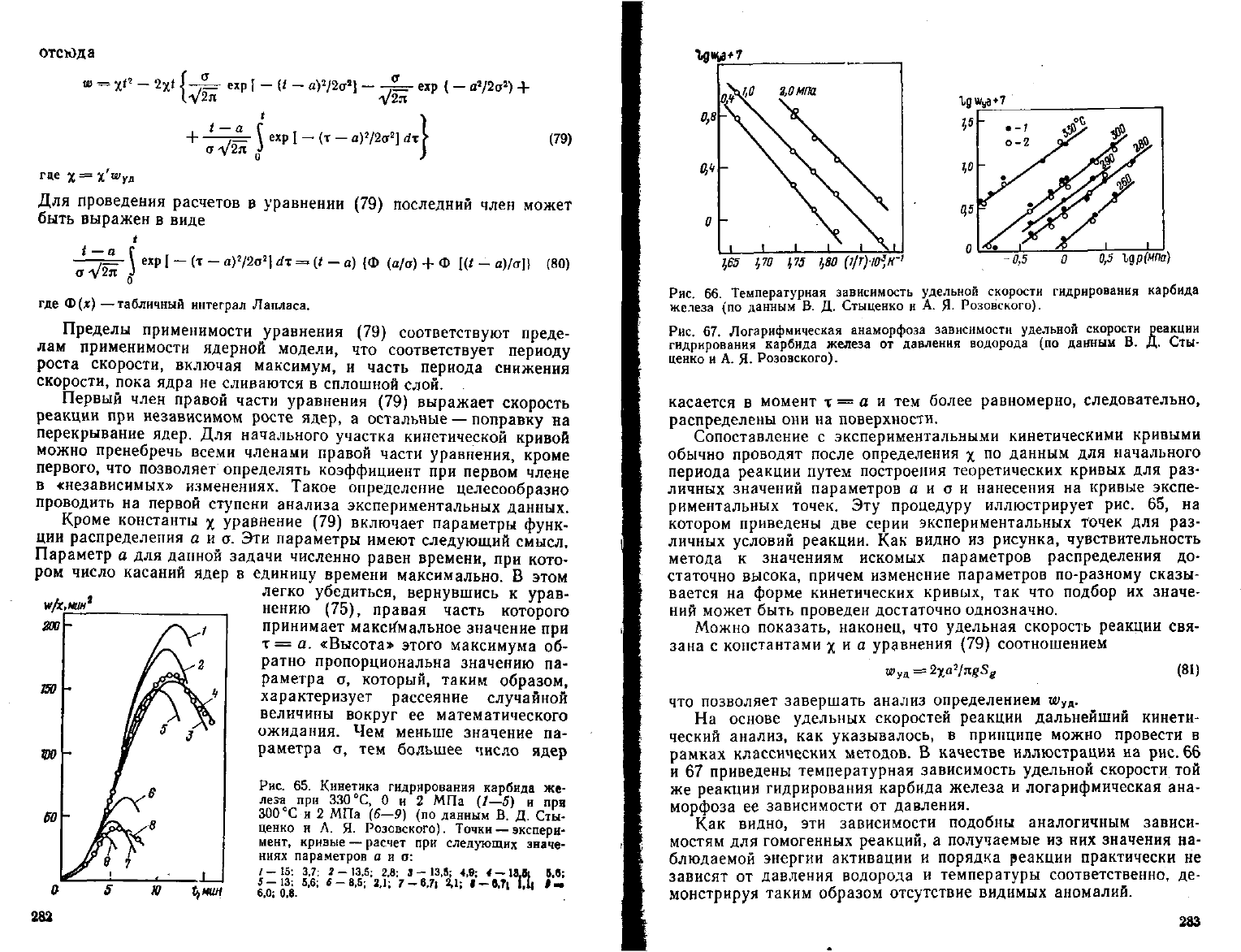
Рис.

65. Кинетика гидрирования карбида же-

леза при 330 "С, 0 и 2 МПа (/—5) и прв

300 °С и 2 МПа (6-9) (по данным В. Д. Сты-

ценко

и А. Я. Розовского). Точки — экспери-

мент, кривые —

расчет

при

следующих

значе-

ниях параметров а и а:

/-15: 3.7: J — 13.5; 2.8: 3 - 13.5; 4,9; 4 — ISA 5.8;

5-13; 5,6; в-8,5; 2.1; 7 - 6,7t 2,1; I - в.?1 Ц| # —

6,0; 0,8.

Цтн

283

lgnw+7

?,80

(?/Т)-Ю*,1Г

-0,5

0,5 Цр(МПо)

Рис.

66. Температурная зависимость удельной скорости гидрирования карбида

железа (по данным В. Д. Стыценко и А. Я. Розовского).

Рнс.

67. Логарифмическая анаморфоза зависимости удельной скорости реакции

гидрирования карбида железа от давления водорода (по данным В. Д. Сты-

ценко

и А. Я. Розовского).

касается в момент х = а и тем более равномерно, следовательно,

распределены они на поверхности.

Сопоставление с экспериментальными кинетическими кривыми

обычно проводят после определения % по данным для начального

периода реакции

путем

построения теоретических кривых для раз-

личных значений параметров а и о и нанесения на кривые экспе-

риментальных точек. Эту

процедуру

иллюстрирует рис. 65, на

котором приведены две серии экспериментальных точек для раз-

личных условий реакции. Как видно из рисунка, чувствительность

метода

к значениям искомых параметров распределения до-

статочно высока, причем изменение параметров по-разному сказы-

вается на форме кинетических кривых, так что подбор их значе-

ний

может быть проведен достаточно однозначно.

Можно показать, наконец, что удельная скорость реакции свя-

зана с константами % и а уравнения (79) соотношением

(81)

что позволяет завершать анализ определением ш

уд

На

основе

удельных

скоростей реакции дальнейший кинети-

ческий анализ, как указывалось, в принципе можно провести в

рамках классических методов. В качестве иллюстрации на рис. 66

67 приведены температурная зависимость удельной скорости той

же реакции гидрирования карбида железа и логарифмическая ана-

морфоза ее зависимости от давления.

Как

видно, эти зависимости подобны аналогичным зависи-

мостям для гомогенных реакций, а получаемые из них значения на-

блюдаемой энергии активации и порядка реакции практически не

зависят от давления водорода и температуры соответственно, де-

монстрируя таким образом

отсутствие

видимых аномалий.

283

РЕАКЦИЯ

ГАЗА С

ПОВЕРХНОСТЬЮ

ТВЕРДОГО ТЕЛА

12. Общие закономерности

Реакции

газа с поверхностью протекают на начальных стадиях

взаимодействия газа с твердым телом. Они

могут

быть самостоя-

тельными процессами в

случаях,

когда по тем или иным причинам

реакция

не может проникнуть в объем твердого тела. Строго говоря,

почти все стадии гетерогенно-каталитического процесса представ-

ляют собой различные реакции газа с поверхностью твердого тела.

Эти

же реакции выступают как гетерогенные стадии в газофазных

радикально-цепных процессах.

Поскольку

протекание реакций газа с поверхностью связано

крайне малыми и потому трудно измеряемыми количествами

превращенного

вещества и в газовой, и в твердой фазе, их

кине-

тические исследования начались сравнительно недавно — в конце

60-х годов. Толчком к этим исследованиям послужило появление

импульсного метода, который в сочетании с хроматографической

или

масс-спектрометрической техникой анализа газовых смесей

превратил одну из труднейших задач кинетического эксперимента

практически рядовую.

Принцип

импульсной методики состоит в том, что в поток

инертного

газа, проходящий через образец твердого вещества (обыч-

но

слой зерен), впрыскивается небольшая порция реагирующего

газа в виде импульса заданной формы, чаще всего приблизительно

прямоугольной. На

выходе

из реактора газовый импульс (вернее,

то,

что от него осталось) анализируют и по изменениям состава

судят

о скорости реакции. Преимущества метода обусловлены воз-

можностями

независимо варьировать время реакции для газового

импульса и для твердого реагента и анализировать отдельную

пробу газа, относящуюся к известному времени реакции.

Действительно, время реакции для газа в режиме идеального

вытеснения

— это время, в течение которого любое (каждое) сече-

ние

газового поршня проходит через весь слой твердого мате-

риала; оно

будет

большим, если слой велик или мала скорость га-

зового потока. Время реакции для твердого реагента — это время,

за которое весь импульс газа проходит через произвольное сечение

твердого материала; оно зависит от скорости газового потока и

объема импульса. Поэтому варьируя соотношение объемов газо-

вого импульса и твердого реагента, мы изменяем соотношение

времен реакции и может подобрать такое, чтобы превращение

газа отвечало требованиям анализа, а превращения поверхности

при

реакции отдельного импульса оставались достаточно малыми.

Недостатки импульсного метода связаны с тем, что заданная

форма

импульса деформируется по мере движения к слою твер-

дого реагента (режим вытеснения не идеален), так что конечное

распределение концентраций достаточно неопределенно.

Итак,

мы подаем импульсы газообразного реагента одина-

ковой

формы и протяженности на поверхность твердого реаген-

281

Какие

процессы

будут

происходить

на

поверхности

^тием частиц твердого

тела?

Пусть

для .

простоты твердое

|о

—

оксид металла

МО, а газ

оксид

углерода

СО, так что про-

ает реакция восстановления оксида

МО -f- СО = М

-+•

COj.

Протекание

реакции приводит

«извлечению»

из

решетки

от-

1ьных атомов кислорода.

При

этом

каждом акте реакции

об-

язуется дефект поверхности.

Из

предыдущих параграфов

мы

|аем,

что в

итоге

результате реакции

на

поверхности

будут об-

(овываться ядра фазы твердого продукта. Каждое ядро

— это

цьшое «образование», включающее значительное число частиц

родукта (атомов металла), структура которых

уже

соответствует

груктуре

продукта.

До

того

как

произошла перестройка струк-

)ы,

эти

частицы существовали

рамках «материнской» решетки

коида

виде стабильной совокупности частиц

—

кластера. Этот

•астер

должен образоваться

результате отдельных актов

ре-

щии.

Следовательно, после образования отдельных дефектов

гагируют

соседние

ними ионы кислорода поверхности,

так что

азникают

группировки дефектов

—

кластеры дефектов.

Образование кластеров дефектов приводит

деформации

крис-

ллической решетки, «сопротивление» которой обусловливает

[еньшение

вероятности реакции

по

мере роста кластеров.

этих

яовиях

будет

наблюдаться уменьшение скорости реакции

во вре-

вни.

Когда кластеры достигнут предельных размеров, реакция

)екратится,

и для

образования ядра,

т. е.

перестройки структуры

lacTepa, потребуется только энергия

—

работа образования

за-

эдыша. Если энергии

системе недостаточно (низкая темпера-

фа),

то

кластер

будет «ждать»

случайного возмущения, необхо-

шого

для

перестройки.

вг Теперь можно предвидеть общий

вид

кинетической кривой взаи-

модействия газа

поверхностью твердого тела.

При

контакте

*а

поверхностью начальная скорость реакции пропорцио-

(альна

концентрации реакционноспособных частиц

на

поверхно-

...

вероятности реакции отдельной частицы. Затем скорость

йакции

должна снижаться

по

мере расходования реакционного-

абных частиц

образования кластеров

до

значений, определяю-

щихся исчезновением дефектов

поверхности

за

счет

их

диффузии

объем твердого тела,

оставаться близкой

стационарной

(или

|йулевой

при

отсутствии обмена

объемом).

Наконец,

образова-

вшем ядер фазы твердого продукта этот период реакции заверша-

$ется,

наблюдается период роста скорости, характерный

для

^объемной*

реакции.

На рис. 68

показана кинетика восстановления Си

О оксидом

^углерода

СО,

наглядно иллюстрирующая применимость таких

рас-

осуждений. Нисходящая ветвь кривой соответствует процессам

об-

разования

восстановленных дефектов

кластеров дефектов

на по-

'Верхности оксида, стационарный участок отражает диффузионный

.обмен

между

поверхностью

объемом Сц

О восходящая ветвь

со-

ответствует

началу образования

роста ядер фазы твердого

про-

235

х,%

монбслоя

Рис.

68.

Типичная кинетическая кривая начальной стадии восстановления CujO

оксидом

углерода

[7,5%

(мол.)

в Не] при 150 °С (по

данным

А. Я.

Розовского,

В.

Д.

Стыценко,

В. Ф.

Третьякова).

Рис.

69.

Кинетика восстановления

при 180 °С

поверхности оксида железа

СО

(мол.)

в Не] (по

данным

А. Я-

Розовского,

В. Д.

Стыценко,

В. Ф.

Третья-

кова).

дукта.

До

начала роста скорости реакция протекает

без

образова-

ния

фаз — в

гомогенной области.

Существует

еще два

типа кинетических кривых взаимодейст-

вия

газа

поверхностью твердого тела. Если образования ядер

фазы

твердого продукта

по тем или

иным причинам

не

происхо-

дит, реакция

«остается»

гомогенной области. Такую картину

можно наблюдать, например,

для

оксидов цинка, ванадия. Возмо-

жен также случай, когда реакция

не

проникает

подповерхност-

ные

слои,

что

чаще всего обусловлено диффузионным торможе-

нием

(времена реакции существенно меньше времен диффузии).

Так

обстоит дело,

частности,

при

восстановлении специально

приготовленного оксида железа,

при

карбидировании железа окси-

дом

углерода.

этом

случае

пределах поверхности монослоя

может быть реализована полная кинетическая картина реакции

газа

твердым телом: образование дефектов

кластеров дефек-

тов, образования ядер фазы твердого продукта,

их

рост

слияние

сплошной слой твердого продукта.

При

этом образуются

«двумер-

ные» поверхностные фазы,

«.толщина»

которых может

не

превы-

шать размеров элементарной ячейки.

На

рис. 69

показана зависимость скорости восстановления

ок-

сида железа

СО при 180 °С от

степени

восстановления поверх-

ности,

иллюстрирующая кинетику реакции

случае

образования

двумерных

фаз на

поверхности твердого реагента. После мини-

мума скорости реакции наблюдается рост скорости, максимум

затем снижение

—и все это в то

время, когда реакция едва

захватывает половину поверхности.

13.

Кинетика реакций газа

поверхностью

Наше

рассмотрение осталось

бы

неполным

без

кинетического

опи-

сания

взаимодействия газа

поверхностью

начальный «доядер-

ный» период. Хотя многообразие возможных

при

этом химических

реакций

необычайно велико, изменения поверхности можно

от-

разить простой схемой.

Для

системы восстановления оксидов

это

следующая совокупность процессов:

образование кислородной

вакансии

при

удалении кислорода;

2) ее

«залечивание» («возвра-

щение

кислорода»), если

системе есть окислитель;

исчезнове-

ние

вакансии

за

счет

ее

диффузии

объем твердого тела (удобно

говорить

диффузии вакансий,

не

забывая

при

этом,

что на

самом

деле

происходит диффузия иона кислорода

из

объема

на

поверхность

—

соответственно вакансия «проваливается»

объем).

Если

окислителя

системе

нет, то

дело ограничивается процес-

сами образования вакансий

и их

диффузии

объем твердого тела.

Хотя

на

самом

деле

задача довольно сложна,

ее

можно

опи-

сать

достаточной точностью упрощенной моделью. Запишем

уравнение баланса вакансий

на

поверхности

dQ/dx = w — v 8 (0) = 0

(82)

где

по—число частиц (например, ионов кислорода

оксиде)

яа

единице

по-

верхности;

б —

безразмерная концентрация вакансий

в долях от /ад ш —

ско-

рость химической реакции;

v —

скорость диффузионного

«стока»

вакансий

объем.

Если

кинетика изучается

помощью импульсного метода, когда

между

импульсами, проходящими

за

время

т,

протекает некото-

рое время

/, в

течение которого диффузионный обмен продол-

жается,

реакция

нет, то

вместо уравнения

(82)

следует

записать

dB/dx = w - vy (83)

(где

у = {t + т)/т) с тем же

начальным условием.

Очевидно,

что

наблюдаемая скорость образования вакансий

—

скорость химической реакции

—

должна быть пропорциональна

количеству оставшихся ионов кислорода

—Q)n

(84)

где ш

отнесена

одной вакансии,

т. е.

представляет собой вероятность

ре-

акции

вакансии

за

единицу времени.

Записать

уравнение

для

скорости диффузионного обмена

между

поверхностью

объемом твердого тела

(а

именно

о нем

мы говорим

как о

скорости

«стока»

вакансий)

куда

сложнее.

не

только потому,

что

пришлось

бы

совместно решать уравне-

ния

диффузии

реакции

нестационарной задаче,

но и

потому,

что

мы не

имеем права описывать интересующий

нас

процесс

уравнением диффузии. Уравнение диффузии применимо, когда

времена процесса достаточно велики, чтобы

он

захватывал стати-

стическое количество слоев

направлении диффузии.

А в

нашем

случае

можно говорить

переходе вакансии

смежный второй

слой,

третий, быть может,

десятый,

но

никак

не в

миллион-

ный,

тем

более

что в

обычных катализаторах, например, таких

слоев

от

поры

до

поры всего несколько десятков.

Следовательно, необходимо найти некий эквивалент, который

позволит

нам

оценить скорость

«стока»

вакансий вместо уравне-

287

ния

диффузии. Для упрощения примем, что во втором слое коли-

чество вакансий настолько мало, что их концентрацию можно

считать равной нулю. Это не такое уж сильное допущение, по-

скольку и в первом слое количество вакансий не более десятков

процентов,

а вакансии, попавшие во второй слой,

будут

«стекать>

и дальше

вглубь.

Теперь, чтобы получить скорость стока вакан-

сий

в объем, мы должны вероятность перехода вакансии из пер-

вого слоя во второй (а она равна удельной скорости диффузии)

умножить на число вакансий и на нормировочный множи-

тель

fioS,

т. е.

v =

(85)

Теперь, подставляя (84) и (85) в (83), получим уравнение, со-

держащее только одну зависящую от времени величину 6.

rfe/rfT

=»

(i-e> -

оудув

(86)

Интегрируя (86), после несложных преобразований найдем

ИЛИ

уд

уд ~Г"

{1 - ехр I - (ш

уд

уоуд)

{1 - ехр — [ю

уд

т + и

уд

(t + т)]}

(87)

(88)

Подставляя значение в в (84), получим выражение для на-

блюдаемой скорости реакции

Шуд/toS

и*

уд

При 1

= 0

уравнение (89) дает начальную скорость реакции

(90)

и окончательно получаем

+ шуд ехр

—

а"=»о

(91)

Уравнение (91) можно также преобразовать к параметриче-

ской

форме, в которой его удобно применять для сопоставления

с экспериментальными данными

(92)

'уд

—

Применимость

уравнения (92) к описанию кинетики восстанов-

ления

оксида меди СиО иллюстрирует рис. 70, на котором экспе-

риментальные данные представлены в линеаризующих координа-

тах. Из уравнения (92)

ясно,

что из такого эксперимента

могут

быть найдены не только значения удельной скорости реакции (на

центр поверхности), но и характеристика диффузионной про-

ницаемости

поверхностного слоя твердого реагента.

В заключение можно заметить, что балансовые уравнения (82)

и (83)

становятся

неприемлемыми,

если превращения

поверхности

288

Рис.

70.

Применимость

уравнения (92) к опи-

санию

кинетики

восстановления поверхности

СиО

оксидом углерода при 150 °С и рсо ~

=?•

4 к.Па (по данным А. Я.

Розовского,

В. Д.

Стыценко,

В. Ф.

Третьякова).

за период реакции отдельного импульса

составляют заметную долю от

всех

час-

тиц

поверхности. В этом

случае

задача

решается аналогичным путем, по как

серия

задач для каждого отдельного им-

пульса и промежутка

между

нмпульса-

-ми

(периода релаксации). При этом ре-

шение

для каждого периода реакции (импульса)

дает

начальное

условие к задаче для последующего периода релаксации, соответ-

ственно решение для периода релаксации — начальное условие

для последующего периода реакции.

В этой главе мы ознакомились с кинетическими описаниями

некоторых типов гетерогенных реакций- реакций газа с жидкостью,

реакций

с участием твердых веществ, реакций

между

газом и

поверхностью твердого тела. Рассмотренные задачи, конечно, не

исчерпывают многообразия гетерогенных реакций; наоборот, они

относятся

к простейшим двухфазным системам. В то же время

при

их решении мы встретились с новыми подходами и методами

кинетического описания, которые в той или иной степени при-

менимы

к разнообразным гетерогенным реакциям. С этим бага-

жом уже можно приступать к самостоятельному анализу. Однако

надо

учесть,

в этой главе обсуждались, главным образом, особен-

ности

развития гетерогенной реакции во времени: закономерности

переноса вещества, часто оказывающие влияние на кинетику

гетерогенных реакций, здесь почти не затрагивались. Они

будут

изложены в следующей главе. Не обсуждалась и проблема ана-

лиза механизма реакции по кинетическим данным. Такой анализ

составляет достаточно специальную область, но после определе-

ния

удельных

скоростей реакции уже не является специфичным

может быть проведен классическими кинетическими приемами.

ГЛАВА

ЭЛЕМЕНТЫ

ДИФФУЗИОННОЙ

КИНЕТИКИ

ХИМИЧЕСКИХ

РЕАКЦИЯ

А.

Я-

Розовский

В гетерогенных системах протекание химической реакции в объ-

еме одной из фаз или па поверхности раздела фаз возможно только

при

условии транспорта реагентов в зону реакции и отвода про-

дуктов реакции. Это значит, что неотъемлемыми стадиями сум-

марного процесса являются и химические, и диффузионные стадии.

•

л»

—Жидкость—

ТОсрдовтело

Рис.

71. Иллюстрация моделей внеш-

ней

(а) и внутренней (б) задач диф-

фузионной

кинетики.

Раздел химической кинетики, изу-

чающий закономерности процес-

сов,

включающих химические и

диффузионные

стадии, называют

диффузионной

кинетикой.

В зависимости от особенностей наложения

друг

на

друга

хими-

ческих и диффузионных стадий различают

внешнюю

внутреннюю

задачи

диффузионной

кинетики. Аппарат внешней задачи исполь-

зуют

в случае, когда диффузия происходит при отсутствии хими-

ческих реакций на всем пути диффузии; химические реакции дей-

ствуют

лишь в конце пути. Аппарат внутренней задачи применяют

ситуации, когда на всем пути диффузии концентрация вещества

изменяется

и вследствие протекания химических реакций, так что

профиль

концентрации диффундирующего вещества определяется

наложением этих процессов.

Для гетерогенных систем характерно разнообразное сочета-

ние

внешней и внутренней задач в разных комбинациях, поэтому

существен правильный выбор модели. Для иллюстрации приведем

один

из простейших примеров. Пусть протекает химическая реак-

ция

газа с твердым телом, погруженным в жидкость в виде от-

дельного куска. При этом газ растворяется в жидкости, и диффун-

дирует

к поверхности куска, (рис. 71). Здесь мы имеем дело с

внешней

задачей.

Разобъем этот кусок на множество более мелких и равномерно

распределим их в жидкости (рис. 71). Теперь

следует

применять

модель внутренней задачи. При дальнейшем усложнении системы,

если например, объединить сосуды, представленные на рис. 71 а

б, и считать, что твердый материал в виде порошка и отдель-

ного куска состоит из разных веществ, причем газ реагирует с

порошком,

а растворенный продукт этой реакции — с отдельным

куском, то «моделирование» такой системы становится неочевид-

ным.

Для этой цели

будут

полезны только что приведенные физи-

ческие (или скорее, геометрические) аналогии.

трудности решения и сами подходы зависят от того, ста-

ционарны

лн процессы в системе. Мы

будем

рассматривать глав-

ным

образом стационарные процессы, в первую очередь гетеро-

генный

катализ.

1. Внешняя задача диффузионной кинетики

Рассмотрим внешнюю

задачу

на примере типичного для гетероген-

ного катализа проточного реактора, заполненного зернами твер-

дого катализатора, на поверхности которого протекает каталити-

ческая реакция. Будем считать, что зерна катализатора непорис-

тые, а линейные размеры поверхности существенно превышают

«90

'длину пути диффузии, так что практически концентрация диф-

фундирующих к (от) поверхности компонентов изменяется в од-

ном

направлении — по нормали к поверхности (так называемая

одномерная задача).

Представим, что газовый поток состоит из ядра, в котором про-

исходит полное смешение, и неподвижной диффузионной пленки

газа толщиной 6, через которую происходит диффузия к внешней

поверхности зерен катализатора. Концентрация с газообразного

реагента в ядре потока поддерживается постоянной. Его концен-

трация

с* у поверхности катализатора меньше с вследствие проте-

кания

реакции; в

результате

этого различия возникает диффузион-

ный

поток реагента к поверхности.

Диффузионный

поток выражается первым законом Фика

j — DSdcfdt (1)

где D —

коэффициент

диффузии; dcfdt—градиент концентрации (в плоскости

нормали

к поверхности).

Скорость

химической реакции определяется концентрацией

газового реагента у поверхности. Очевидно, что концентрация

у поверхности

будет

изменяться во времени до тех пор, пока ско-

рости реакции и диффузии

будут

отличаться

друг

от

друга.

Если,

например,

скорость диффузии больше скорости реакции, концен-

трация

реагента у поверхности

будет

возрастать во времени.

При

этом скорость диффузии

будет

снижаться (из-за уменьшения

градиента концентрации), а скорость реакции — увеличиваться.

При

наличии таких связей со временем установится стационарная

концентрация

реагента у поверхности катализатора, а скорости

реакции

и диффузии

будут

равны. При этом установится распре-

деление концентраций реагента в плоскости нормали к поверх-

ности

катализатора, показанное на рис. 72, а.

Из

рисунка ясно, что градиент концентрации реагента опреде-

ляется выражением

dc/dt « (с - с')}Ь (2)

Запишем

условие стационарности

Ddcjdl

— шуд(с')-»0

учетом

(2)

(С — С

) ям О)уд (с')

(3)

(4)

где р »* D/fl — константа скорости диффузии.

Из

уравнения (4), в частности,

следует,

что при прочих равных

условиях соотношение

между

концентрациями реагента в ядре

Рис.

72. Примерный вид

профиля

концентрации

реагента в плоскости

нормалв

к внешней поверхности зер-

на:

внешняя

(а) и внутренняя (б)

«адачи диффузионной

кннетнкн.

10*

Ср О.

291

потока и у внешней поверхности зерна определяется видом

кине-

тического уравнения собственно реакции.

Для реакции первого порядка ш

уд

= /м/, и из уравнения (4|

получаем

Тогда удельная скорость реакции составит

уд - *Р<У(* + Р) (5)

Уравнение (б) хорошо отражает свойства модели. Если k <C p

величиной

к в знаменателе можно пренебречь, и уравнение (б)

обращается в исходное уравнение реакции первбго порядка.

В этом

случае

говорят, что реакции протекает в кинетической

рбласти.

Если,

наоборот, k "> р уравнение (б) обращается в

(в)

уд

V**/

так

что наблюдаемая скорость химической реакции полностью

^определяется скоростью диффузии. При этом концентрация реаген-

та у поверхности зерна близка к нулю. Область (совокупность

условий)' протекания реакции, в которой реализуется последнее

.неравенство и соответственно уравнение (6), называют

внешне-

диффузионной

областью,

а соответствующее снижение скорости

реакции

—

внешнедиффузионным

торможением.

В промежуточном случае, когда значения констант скорости

реакции

и диффузии соизмеримы, реакция протекает в переходной

области (между кинетической и внешнедиффузионной).

Поскольку

скорость диффузии зависит от концентрации в пер-

вой

степени, во внешнедиффузионной области реакция любого ки-

нетического порядка

будет

протекать как реакция первого поряд-

ка,

т. е. подчиняться уравнению (6). Уравнением (6) определяются я

основные

свойства реакций, протекающих во внешнедиффузионной

области. Константа скорости диффузии в газовой фазе очень слабо

зависит от температуры (наблюдаемая энергия активации поряд-

ка

нескольких килоджоулей на моль против десятков и сотен кило-

джоулей на моль для химических реакций). Так же

ведет

себя

наблюдаемая скорость реакций во внешнедиффузионной области.

В переходной области наблюдаются промежуточные эффекты.

Константа

скорости диффузии зависит также от газодинамиче-

ских параметров; она возрастает с увеличением линейной скорости

потока газа и уменьшением размеров зерен (улучшается пере-

мешивание и уменьшается б). Поэтому соответствующими при-

емами пользуются как для оценки влияния внешнедиффузионного

торможения,

так и для его устранения — повышение линейной ско-

рости газового потока, например, позволяет перевести реакцию из

внешнедиффузионной

области в кинетическую. При повышении

температуры k растет значительно сильнее, чем р, и влияние диф-

фузионного торможения усиливается.

В системах гетерогенного катализа модель внешней задачи со-

ответствует

диффузии газа из ядра потока к внешней поверхности

292

верна катализатора, и внешнедиффузионное торможение наблю-

дается довольно часто. Поэтому исследование кинетики каталити-

ческой реакции обычно начинают с оценки влияния внешнедиф-

фузионного торможения при вариировании линейной скорости

газового потока (при постоянной объемной скорости, т. е. пропор-

ционально

изменяя скорость потока и навеску катализатора).

Линейную скорость увеличивают до тех пор, пока не перестает

наблюдаться ее влияние на скорость реакции — внешнедиффузион-

ное

торможение

отсутствует.

Поскольку внешнедиффузионное тор-

можение возрастает с повышением температуры, такая оценка

должна быть сделана для наивысшей температуры из предпола-

гаемого температурного интервала.

Использованный

здесь

подход

к решению задачи был сформу-

лирован Д. А. Франк-Каменецким и получил название

метода

рав-

нодоступной

поверхности.

2. Внутренняя задача диффузионной кинетики

Модель внутренней задачи, как было показано в начале главы,

характерна для систем с равномерным распределением реагента

или

катализатора в объеме, в котором происходит диффузия.

В гетерогенном катализе чаще всего эта модель описывает диффу-

зию реагентов в

глубь

пористого катализатора (и соответственно

диффузию продуктов в обратном направлении).

Твердые катализаторы обычно представляют собой высокопо-

ристые тела, удельная поверхность которых достигает значений

10—100

/г и намного превышает геометрическую поверхность

зерен (1—10см

/г). Поэтому каталитическая реакция протекает

главным образом внутри зерен катализатора и обеспечивается диф-

фузией реагентов сначала к внешней, а затем к внутренней поверх-

ности

зерен вдоль пор. По мере проникновения в

глубь

зерна ре-

агенты расходуются в реакциях на стенке поры, поэтому необхо-

димо использовать модель внутренней задачи.

Примем,

что пористая

структура

однородна и непрерывна, т. е.

что

структура

во

всех

частях зерна одинакова и все поры сооб-

щаются

между

собой.

Рассмотрим модельную пору, направленную вдоль максималь-

ного градиента концентраций реагента (от внешней поверхности к

центру зерна, в середину плоской пластины и т.д.). Влияние фор-

мы зерна может быть отражено формой модельной поры. Для сфе-

рических зерен модельной является коническая пора, для диффу-

зии

в плоскую пластину — цилиндрическая пора).

Составим дифференциальное уравнение, описывающее распре-

деление концентраций в цилиндрической поре радиуса г. Очевидно,

что это же уравнение

будет

описывать изменение концентрации

плоской пористой пластине по направлению нормали к поверх-

ности.

Рассмотрим бесконечно малый элемент поры длиной dl. При-

рост количества вещества (реагирующего газа] в этом элементе

результате

диффузии

будет

равен разности

между

диффузион-

ными

потоками в рассматриваемый элемент (со стороны внешней

поверхности) и из него и составит [см. уравнение (1)]

(7)

где лг* —

сечение

модельной

поры

—

поверхность,

через

которую

происходит

диффузия.

Скорость химической реакции, протекающей на стенке поры,

будет

пропорциональна ее поверхности, которая для рассматривае-

мого элемента составит

2nrdl,

так что

dm « ю

д dS =» kf (с) 2пг dl (8)

Тогда можно записать итоговое уравнение баланса реагирую-

щего газа для рассматриваемого объема

4ldctdt

nr*D%£r-dt-

Используя

условие

стационарности

{dc/dt^Q),

получим

(9)

(Ю)

Граничными условиями для уравнения (10)

будут

dc/dl

= 0 при / =» L

(условие

симметрии)

с="С

при /=*0

где

Со

—

концентрация

реагента

входа

модельную

пору;

L —

длина

модель-

ной

поры

(половица

толщины

пластины).

Уравнения (9) и (10) —это уравнения соответственно неста-

ционарной

и стационарной диффузии с источниками (стоками) для

модельной поры. В нашем

случае

в качестве источника выступает

химическая реакция.

Поскольку уравнение (10) не всегда имеет аналитические ре-

шения

[в зависимости от вида функции

f(c)],

попытаемся из его

вида оценить

структуру

определяющего параметра. Для этого

представим уравнение в виде

где

(И)

(12)

Отсюда

ясно,

что решение

будет

содержать наряду с концентра-

цией

параметр, определяемый уравнением (12) в виде функций

верхнего и нижнего граничных условий (пределов интегрирова-

ния).

Как мы видели, одно из них нуль, а второе L, т.е. опреде-

ляющим параметром должен быть

Ь —

1*1ЩтЪ

(13)

который,

возможно, включает и функцию от концентрации с.

Для реакции первого порядка нетрудно получить аналитиче-

ское решение задачи. В этом

случае

уравнение (11)

будет

иметь вид

294

(15)

с граничными условиями

dc/dh

= 0 при k

=» h

с«=с

при Л* = 0

Уравнения такого типа решаются при помощи подстановки

=>Y

(16)

после которой интегрирование проводится без существенных

труд-

ностей.

Получаемое решение удобно представить в виде отноше-

ния

наблюдаемой скорости реакции к скорости, которая наблюда-

лась бы в отсутствие внутридиффузионного торможения (т. е. в

отсутствие падения концентрации реагента в поре).

f^wjw

(17)

Это отношение называют

фактором

диффузионного

торможе-

ния, относительной глубиной проникновения реакции, степенью

доступности поверхности.

Для реакции первого порядка

f =

th(A)/A

(18)

Соответственно формуле (18) наблюдаемая скорость реакции,

осложненной внутридиффузионным торможением, определится вы-

ражением

'~^th

(h)c

(19)

где S —

внутренняя

поверхность

пор,

которая

хорошей

точностью

равна

удельной

поверхности

катализатора.

Из

приведенных формул

следует,

что влияние внутридиффу-

зионного

торможения на наблюдаемую кинетику реакции опреде-

ляется величиной безразмерного параметра ft, значение которого

зависит от структурных факторов (радиуса пор, линейного раз-

мера зерен) и от соотношения

между

константой скорости реакции

коэффициентом диффузии. Последнее обусловливает зависимость

параметра Л от температуры. Фактор диффузионного торможе-

ния

/, согласно формуле (18), определяется исключительно вели-

чиной

параметра h.

В формулу (18)

входит

гиперболический тангенс, который за-

висит от значений аргумента следующим образом, При малых А

(Л < 0,2)

th (А) да h (20)

так

что f « 1. В этом

случае

практически можно пренебречь влия-

нием

внутридиффузионного торможения на наблюляомую

кине-

тику реакции

{кинетическая

область)

При

больших h (ft ^ 2)

th(A)«l

fftsl/A

(21)

В этом

случае

наблюдаемая скорость реакции становится про-

порциональной

среднему геометрическому из константы скорости

295

реакции

коэффициента диффузии. Поскольку последний слабо

аавнсит

от

температуры (если диффузия происходит

газовой

фазе),

наблюдаемая энергия активации

будет

составлять примерно

половину

ее

истинного значения. Соответствующую макрокинети-

ческую область протекания реакции называют

внутридиффузион-

ндй

областью.

Скорость реакции, протекающей

во

внутридиффу-

зцонной

области, зависит

от

размеров зерен твердого материала

от

среднего радиуса

пор.

Как

видно

из

условия

выражению

(21),

значение фактора

диффузионного торможения

для

внутридиффузионной области

/ ^

«^ 0,5. В

этом

случае

концентрация газообразного реагента

окрестности центра зерна оказывается близка

нулю

и для

внутридиффузионной области уравнение типа

(10)

может

ре-

шаться

боле* простыми граничными условиями:

с-с

при /-0

— 0 прн / — £ * '

Применение

граничных условий

(22)

существенно упрощает

решение, поэтому

с их

использованием

для

реакций

со

сложной

кинетикой

можно получать аналитические решения, применимые,

естественно, только

для

внутридиффузионной

(но не для

пере-

ходной) области протекания реакции.

Интервал значений

h (0,2 < Л < 2)

соответствует реакции,

протекающей

переходной области.

Для

последней,

как и в слу-

чае внешней задачи, характерны промежуточные закономерности,

р частности, значения наблюдаемой энергии активации

этой

области лежат

интервале

между

истинным значением

и его

половиной.

Для реакций

других

кинетических порядков закономерности

влияния

внутридиффузионного торможения аналогичны описан-

ным,

с той

лишь разницей,

что по

мере «погружения»

во

внутри-

диффузионную область изменяется концентрационная зависимость

скорости реакции: наблюдаемый порядок реакции приближается

среднему арифметическому

между

первым

истинным.

Если зависимость скорости реакции

от

концентрации реагента

можно выразить степенной функцией вида

да

Н* (23)

(реакция

n-го

порядка),

то

величина безразмерного параметра

определяется формулой

— I V^A/r^ff""

(24)

а наблюдаемая скорость реакции

во

внутридиффузионной области

""•

vfn"'

/Ss

(25)

Сложнее обстоит дело

для

реакций

«ленгмюровской» кинети-

кой

вида

часто встречающихся

гетерогенном

ферментативном (уравне-

ние

Михаэлиса —- Ментен) катализе

широко обсуждавшихся

книге.

Аналитическое решение

этом

случае

может быть получено

только

двумя упрощающими ограничениями: реакция протекает

во внутридиффузионной области [первое ограничение,

ведущее

за

собой более простые граничные условия

(22)] в

дифференциаль-

ном

реакторе (второе ограничение, позволяющее

не

проводить

ин-

тегрирование

по

длине слоя катализатора).

При

этих условиях

величина фактора диффузионного торможения определяется фор*

мул

ой

/=--—^VSfup-lnd-fM)

(27)

а наблюдаемая скорость реакции

во

внутридиффузионной области

V-,

[Ьр-\п(\

(28)

Как

видно, формулы

(27) и (28)

далеки

от

простых соотноше-

ний,

наблюдавшихся

для

реакций первого

или п-то

порядка.

Однако наблюдаемая скорость реакции

во

внутридиффузионной

области по-прежнему пропорциональна

•yJkD*

что

ведет

за

собой

соответствующие изменения наблюдаемой энергии активации.

Впрочем,

следует

напомнить,

что

коэффициент

тоже зависит

ох

температуры, вследствие этого

будет

искажать значения наблю-

даемой энергии активации.

Для общего случая реакций

«ленгмюровской» кинетикой

из*

вестно приближенное решение (согласующееся

предельных

си-

туациях первого

нулевого порядка

со

строгими решениями),

со-

гласно которому фактор диффузионного торможения равен

(29)

(Ьр/2)

наблюдаемая скорость реакции

во

внутридиффузионной области

составляет

пгр

2krD

(30)

Существенно,

что

интегрирование уравнения

(30)

может при-»

вести

уравнениям того

же

вида,

что и

обсуждавшиеся

преды-

дущих

главах

для

реакций

потоке. Поэтому

при

кинетическом

описании

гетерогенной каталитической реакции

потоке оценка

влияния

внутридиффузионного торможения становится

тем

более

обязательной.

Макрокинетические области гетерогенно-

каталитической реакции

Как

отмечалось, гетерогенно-каталитическая реакция может

про-

текать

кинетической,

во

внешнедиффузионной,

во

внутридиф-

фузионной

и в

соответствующих переходных областях. Этим

на-