Орленок В.В. Основы геофизики

Подождите немного. Документ загружается.

ционально расстоянию r, вторая – квадрату расстояния r

. Отсюда сле-

дует, что на расстояниях r, больших по сравнению с длиной волны λ,

второе слагаемое становится малым по сравнению с первым; им можно

пренебречь:

=−













sin . (VIII.41)

Акустическое давление сферической волны определяется из выраже-

ния

. sinsin

cos













−=













−=

























−−=−=

ρωω

∂

(VIII.42)

Для случая r>>λ отношение акустического давления к колебатель-

ной скорости равно:

, (VIII.43)

т.е. вдали от источника акустическое сопротивление сферической вол-

ны равно акустическому сопротивлению плоской волны.

Следовательно, для больших расстояний от источника, равных де-

сяти длинам волн, сферичностью фронтов можно пренебречь и рас-

сматривать сферические волны как плоские.

Интенсивность сферической волны вдали от источника определя-

ется из выражения:

IPV

, (VIII.44)

где P

и V

– амплитуды акустического давления и колебательной ско-

рости прямой сферической волны вдали от источника. Из (VIII.41) и

(VIII.42) видно, что

ρω

; V

(VIII.45)

или

22 r

ωρρω

== . (VIII.46)

Таким образом, интенсивность сферической волны в однородной

непоглощающей среде убывает обратно пропорционально квадрату

расстояния от источника. С физической стороны это соответствует

увеличению волновой поверхности при удалении от источника.

Мощность, переносимая сферической волной вдали от источника,

определяется как произведение интенсивности на сферическую по-

верхность S:

W=IS, (VIII.47)

так как Sr= 4

ωρ

= , k =

, то

ωρπ

4 A

W = . (VIII.48)

Следовательно, мощность излучения пропорциональна квадрату

амплитуды и обратно пропорциональна длине излучаемой волны.

§5. Отражение волн на границе вода – дно

Эта чрезвычайно важная задача позволяет понять физику процесса

формирования звукового поля выше и ниже границы раздела вода-дно

в океане. Впервые она была решена в полной мере для продольных и

поперечных волн Л. М. Бреховским (1957). Здесь мы дадим упрощен-

ное решение этой задачи.

Рассмотрим случай, когда образование поперечной волны в мор-

ском грунте не происходит. С физической точки зрения такая задача

соответствует отражению волны от границы двух жидких сред. В пер-

вом приближении такой подход дает удовлетворительное решение для

оценки условий формирования отражений на границе вода-дно и одно-

временно упрощает анализ.

Предположим, что источник колебаний (взрыв) находится в вод-

ном слое, откуда прямая волна U, падая на границу z, разделяющую

две среды с разным акустическим импедансом –

, образует

отраженную волну U

и проходящую под дно (преломленную) волну

(рис. 59). Представим волны U

, U

в виде составляющих векто-

ра К по осям координат x, z (плоская задача). Вектор K будет перпен-

дикулярен поверхности волнового фронта и определяет направление

луча:

= cos

; KK

= sin

KKK

222

=+= =













ωπ

. (VIII.49)

218

С учетом этого решение волнового уравнения для падающей U

, отра-

женной U

и преломленной волн U

будет иметь вид:

Uft

=−

−













sin cos

αα

, (VIII.50)

URft

=−













sin cos

αα

, (VIII.51)

UWft

=−

−













sin cos

ββ

. (VIII.52)

Здесь R – коэффициент отражения от дна, W – коэффициент пре-

ломления;

– углы паде-

ния, отражения и преломле-

ния; c

– скорость звука

выше и ниже границы раздела

(дна моря).

Выберем начало коорди-

нат на границе, т.е. z = 0. Так

как среда непрерывна, то нор-

мальные смещения на границе

, U

и U

также непрерывны

и равны

+ U

= U

. (VIII.53)

Давление P также должно

быть равно по обе стороны от

границы, так как в противном

случае среда на границе z = 0

будет терпеть разрыв и волна

в пространство

не прой-

дет. Так как

∂

, (VIII.54)

то равенство давлений можно записать так:

(

)

∂

. (VIII.55)

Рис. 59. Отражение звука дном моря

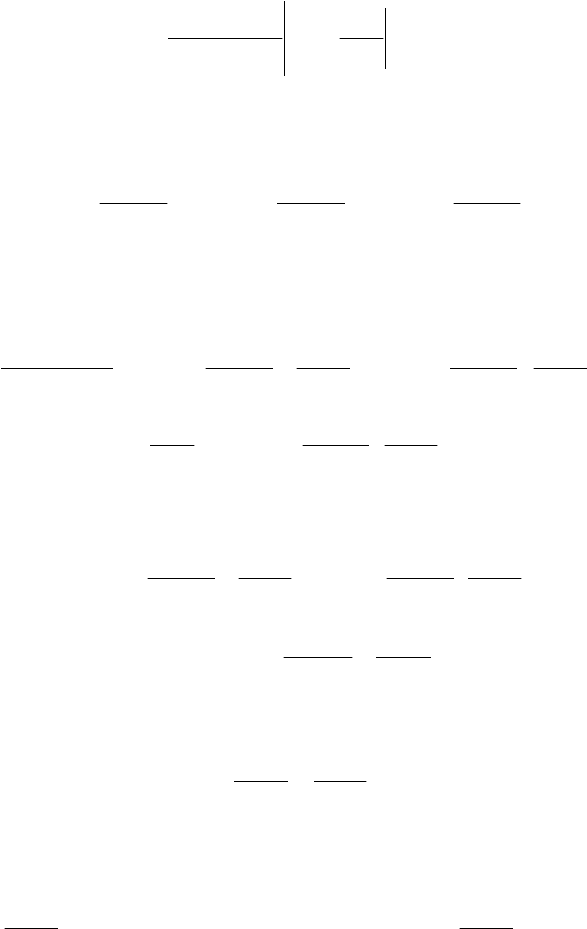
219

Горизонтальные смещения равны нулю, т.е. мы предполагаем среды по

обе стороны границы жидкими:

()

∂

−=

. (VIII.56)

С учетом (VIII.50, VIII.51, VIII.52) полное звуковое поле на границе

вода-дно будет иметь вид:

Rf t

Wt t

−













+−













=−













cos cos

cos

αα

112

. (VIII.57)

Продифференцируем обе части выражения (VIII.57) согласно гранич-

ному условию (VIII.55):

()

∂

αα αα

Rf t

11 11

=−













⋅−−













cos cos

;

∂

ββ

Wf t

=−













cos cos

С учетом (VIII.55) получим:

coscos

1111

tWfc

tRf

tfc

ββ

αααα

⋅













−=

























−−⋅













−

(VIII.58)

Поскольку имеет место соотношение Снеллиуса:

cos

= , (VIII.59)

то подставим его в уравнения (VIII.57) и (VIII.58) с учетом граничных

условий (VIII.55). Можно сократить в (VIII.57) обе части уравнения на

ft z

−













cos

, а в уравнении (VIII.58) – на

ftz

cos

−













В результате получим систему двух уравнений с двумя неизвест-

ными R и W:

220

()

−=











cos

или

11 2 2

−=







cRcW

ρα ρ β

cos ( ) cos

. (VIII.60)

Подставим первое уравнение во второе

11 2 2

11cRcRcos ( ) cos ( )

−

Решая его относительно R, получим:

−

ρβρα

22 11

cos cos

. (VIII.61)

Аналогично находим W:

22 11

ρβρα

cos

cos cos

. (VIII.62)

Полученные уравнения позволяют определять коэффициенты отраже-

ния и преломления от границы вода-дно при любых углах падения.

Они показывают, что эти коэффициенты зависят от акустических им-

педансов среды по обе стороны границы и углов падения и преломле-

ния.

Для случая нормального падения волны на границу раздела, когда

cos cos

1, получим известные формулы Рэлея:

−

ρρ

22 11

; (VIII.63)

22 11

ρρ

. (VIII.64)

Проанализируем полученные выражения для коэффициентов отраже-

ния и преломления в случае нормального падения волны на границу

раздела.

Перепишем выражение (VIII.63) в виде:

221

−

. (VIII.65)

Как видно из (VIII.65), коэффициент отражения R от дна обраща-

ется в нуль при равенстве акустических жесткостей

11 2 2

в сре-

дах по обе стороны от границы z = 0. Если акустическая жесткость

в нижней среде много выше

, то R = 1, т.е.

2211

при,0

0 при,1

ρρ

≈

≈ . (VIII.66)

Коэффициент преломления при аналогичных условиях приобретает

следующие значения:

2211

при,1

0 при,0

сс

ρρ

≈

≈ .

Первое условие для

≈ 0 в реальных средах не имеет смысла, так

как морская вода характеризуется конечными вещественными значе-

ниями

и c

(

≈ 1,03 г/см

, с ≈ 1500 м/с). Это условие может быть в

первом приближении реализовано, если

. Проведенный

анализ показывает, что при равенстве акустических жесткостей воды и

пород дна (что может иметь место в случае рыхлого, водонасыщенного

грунта) коэффициент преломления равен:

≈

, (VIII.67)

а коэффициент отражения равен нулю, т.е. отражения от такого грунта

не будет совсем. Однако коэффициент преломления, как это видно из

(VIII.67), в этом случае равен единице, т.е. волна полностью, без иска-

жений и потерь пройдет в грунт, как если бы никакой границы не бы-

ло. Коэффициент отражения R приобретает максимальное значение,

222

равное единице, в случае резкого перепада акустических жесткостей на

границе раздела вода-дно. Это имеет место, если последнее сложено

весьма плотными породами – гранитами, базальтами и др. Аналогич-

ный резкий перепад

происходит на свободной поверхности

моря.

Приведем два примера. Акустические сопротивления морской во-

ды и воздуха равны соответственно

= 1,0⋅ 1,5⋅ 10

;

= 429. Ко-

эффициент отражения на границе воздух-вода при падении из воды в

воздух равен:

.00057,0

,99943,0

42910511

10152

≈

−≈

+⋅⋅⋅

⋅⋅−

Следовательно, 99% энергии падающей волны отражается от поверх-

ности моря с обратным знаком, т.е. поверхность моря является практи-

чески зеркальным отражателем акустической энергии. Поэтому звуки в

воде практически не слышны над морем. Для границы вода-базальт

получаем:

= 1,5⋅ 10

= 3,0⋅ 6,5⋅ 10

; R = 0,86, т.е. примерно 5/6

падающей на границу энергии волны отражается, и лишь 1/6 проходит

в грунт. Этот факт хорошо известен в морской сейсмоакустике и эхо-

лотировании. Плотные грунты всегда дают более четкую запись отра-

жений, чем мягкие осадочные грунты (рис. 60).

Коэффициент отражения меняет знак на обратный, если величина

, т.е.

. Перемена знака происходит при падении вол-

ны из среды с большим акустическим сопротивлением в среду с мень-

шим акустическим сопротивлением. Это, в частности, имеет место при

отражении от свободной поверхности моря, при подходе волны снизу.

§6. Отражение звука от слоя

Рассмотрим задачу об отражении плоской волны от однородного

слоя толщиной h, падающей под горизонтальным углом α

на верхнюю

и нижнюю границу слоя (рис. 61). Будем полагать, что среды 1 и 3,

разделяемые слоем h, также являются однородными, т.е. распределе-

ние скорости и плотности в них по z и по x постоянны. Решение задачи

впервые было изложено в работе Л. М. Бреховских (1957). Им мы и

воспользуемся.

223

224

Эта задача имеет важ-

ное приложение для сейс-

моакустики и гидроаку-

стики. В частности, таким

слоем можно аппрокси-

мировать толщу океани-

ческих осадков, подсти-

лаемых базальтовым фун-

даментом, что справедли-

во для волн низкой часто-

ты, соизмеримых с мощ-

ностью осадочной толщи,

либо с каким-нибудь

верхним слоем осадков,

например, до первой от-

ражающей границы (гори-

зонт А). Мощность этого

неконсолидированного

слоя в океане в среднем

меняется в пределах 150 – 300 м.

При прохождении волны через слой происходит интерференция

(сложение) колебаний от верхней и нижней границ слоя. Поэтому для

результирующего акустического поля в слое h можно написать сле-

дующее выражение:

()

UWe Re e

ik z ik z ik x

22 2

22 2222

− cos cos sin

ααα

. (VIII.68)

Ранее было показано, что отношение акустического давления к колеба-

тельной скорости при нормальном падении плоской волны на границу

раздела двух сред характеризует волновое сопротивление (импеданс)

среды (

c). При произвольном падении α

cos

. (VIII.69)

Здесь мы обозначим акустический импеданс буквой γ, чтобы не путать

с координатой z.

При смене направления распространения волны cosα меняет знак и

=−

. (VIII.70)

Рис. 61. Отражение звука от тонкого слоя

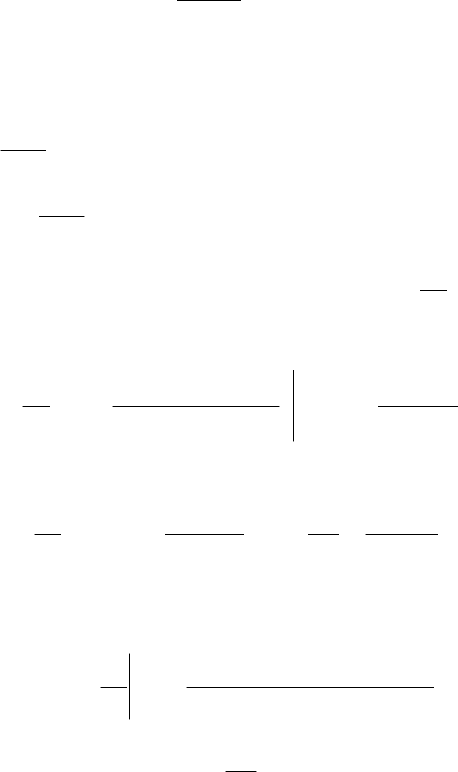
225

В соответствии с этим будем считать, что среды 1, 2, 3 (рис. 61) харак-

теризуются импедансом:

cos

, где j=1, 2, 3... (VIII.71)

Найдем акустическое давление и колебательную скорость, создавае-

мые результирующим полем U

в слое h (Бреховских, 1957):

(

)

()

;cos

222222

sincos

cos

sincos

cos

222

ααα

ωρ

∂

ωρ

∂

xikzikzik

eeReWi

eeReWik

⋅+−=−=

⋅−=−=

−

(VIII.72)

В соответствии с формулой (VIII.69) отношение

на границе z=0

должно равняться импедансу среды 1, т.е.

WRe

ikz

−













−

γγ

cos

, (VIII.73)

откуда

−

γγ

, или

−

γγ

. (VIII.74)

На верхней границе слоя, т.е. при z = h, из выражений (VIII.72)

имеем:

αα

22 22

−

We Re

ihk ihk

cos cos

, (VIII.75)

Подставляя в (VIII.75) значение

из (VIII.74) после простых преоб-

разований с учетом формулы Эйлера:

cos sin

ϕϕ

±=

, (VIII.76)

получим: