Орленок В.В. Основы геофизики
Подождите немного. Документ загружается.


206
где
ρ
– плотность, г/см
3
, с – скорость упругих волн м/с. Величина
∂
∂
U
x
〉0, когда под влиянием внешней силы
σ
x
частицы среды сбли-
жаются, т.е. происходит сжатие среды. При
∂
∂
U
x
〉0 частицы среды
отходят друг от друга и возникает растяжение.
Поскольку величина
σ
x
представляет собой давление Р, то закон
Гука позволяет рассчитать акустическое давление в любой точке сре-
ды.
Рис. 56. Деформации объема среды при движении P-волн (а); деформации
сдвига при движении S-волн (б)
Если деформация вызывает касательное напряжение (см. рис. 56),
то она определяется углом сдвига α или деформацией сдвига
δ
, где
δ
α
= tg
, или
δ
=
∆d
d
:
τ
δ
=
G . (VIII.7)
Здесь G – модуль сдвига. Это закон Гука для сдвиговых деформаций,
или деформаций формы.
Закон Гука в своей линейной части (см. рис. 57) характеризует об-
ласть упругой деформации, происходящей в малом отрезке времени
(доли секунды). Однако упругое тело Гука в геологическом масштабе
времени (тысячи, миллионы лет) может вести себя как пластичное те-
207
ло, т.е. подчиняться нелиней-
ным законам Максвелла. Та-
кую среду называют телом
Максвелла. В общем случае
деформация в твердых поро-
дах слагается из упругой f
1
(
σ
)
и пластичной f
2
(
σ
,t), т.е.:
∆U = f
1
(
σ
) + f
2
(
σ
,t). (VIII.8)
Таким образом, горные
породы в разных временных
масштабах могут одновремен-
но рассматриваться и как уп-
ругие тела Гука, и как пла-
стичные тела Максвелла. Если
величина деформации превы-
шает пределы прочности по-
род, то наступает их разруше-
ние. Величина таких деформаций слишком велика и выходит далеко за
пределы условий возбуждения малых (гармонических) колебаний. По-
этому мы их здесь не будем рассматривать.
Модуль Юнга Е и модуль сдвига G являются основными упругими
характеристиками среды. Их размерность – кг/см
2
или н/м
2
(СИ). Для
оценки отношения между продольными (∆U/U) и поперечными (∆d/d)
деформациями вводится коэффициент Пуассона (безразмерная вели-
чина):
χ
=
−
EG
G
2
2
. (VIII.9)
Весьма важно отметить, что через модуль Юнга и модуль сдвига
можно определить скорость распространения упругих волн – объем-
ных, называемых продольными волнами с
р
– и сдвиговых волн, назы-
ваемых поперечными волнами – с
s
:
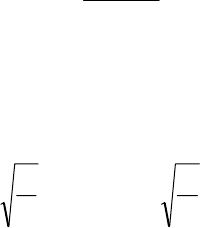
ρ
E
c
p
= (м/с);
ρ
G
c
S
= (м/с), (VIII.10)
где
ρ
– плотность среды.
Существует весьма важное соотношение скорости продольных
волн к скорости поперечных – с
р
/с
s
, которое является, по существу,
функцией коэффициента Пуассона:
Рис. 57. К иллюстрации закона Гука:
ОА – область упругой деформации;
АВ –область пластичной деформации

208
χ
χ
21
1
2
−
−
=
S
P
c
c
. (VIII.11)
Для осадочных пород, вследствие низкого сопротивления сдвигу рых-
лых отложений, величина с
р
/с
s
может достигать больших значений:
с
р
/с
s
= 1,4 ÷ 14 и более.
Для кристаллических магматических и метаморфических пород это
соотношение лежит в более узких пределах:
с
р
/с
s
= 1,7 ÷ 1,9.
Из приведенного видно, что скорость упругих волн в породах за-
висит главным образом от их плотности и практически не зависит от
частоты колебаний. Последняя оказывает сильное влияние на погло-
щение волн.
§2. Волновое уравнение
Если к горной породе приложить внешнюю силу, вызывающую
напряжение (взрыв), то, как было показано выше, произойдет дефор-
мация, смещение частиц породы на расстояние x в направлении дейст-
вия силы F(
σ
). Так как частицы пород жестко связаны между собой
таким образом, что смещение одной частицы вызывает смещение дру-
гой и т.д. (принцип домино), произойдет распространение упругой
гармонической деформации с некоторой скоростью. Найдем уравнение
возникающих при этом гармонических колебаний частиц. Для просто-
ты ограничимся вначале случаем, когда напряжение действует вдоль
одной координаты x. Согласно второму закону Ньютона,
ma=F, (VIII.12)
где а – ускорение, m – масса частицы,
2
2
t
U
a
∂
∂
= . (VIII.13)
Величина U = x характеризует смещение частиц от некоего положения
равновесия. Обозначим массу частицы как произведение объема V на
плотность
ρ
:
m = V·ρ = ∆x∆y∆z·ρ. (VIII.14)

209
Перепишем выражение (VIII.13) с учетом (VIII.14) и (VIII.15):
2
2
2
2
t
U
zyx
t
U
mF
∂
∂
ρ
∂
∂
∆∆∆== . (VIII.15)
Если силы действуют вдоль одной оси x, то сумма всех сил F будет
равна сумме напряжений
σ
x
, действующих на соответствующую пло-
щадь (объем) S:
F
x
S
x
∑
=
∂
σ
∂
, (VIII.16)
где S = ∆x∆y∆z.
Подставим (VIII.16) в левую часть уравнения (VIII.15) и после со-
кращения получим:
).(
2
2
V
m
xt
U
x
=
=
ρ
∂
∂σ
ρ
∂
∂
(VIII.17)
Теперь воспользуемся законом Гука (VIII.4):
.; где
,
E
x
U
x
U
E
xx
xx
∂
∂
σ
∂
∂
ε
εσ
==
=
(VIII.18)
В итоге получаем волновое уравнение вида:
∂
∂
ρ
∂
∂
2
2
2
2
U
t
EU
x
=
. (VIII.19)
Здесь коэффициент
E
ρ
есть не что иное, как квадрат скорости распро-
странения продольной волны в породе с
p
:
c
E
p
=
ρ
, (VIII.20)
или
∂
∂
∂
∂
2
2
2
2
2
U
t
c
U
x
p
= . (VIII.21)
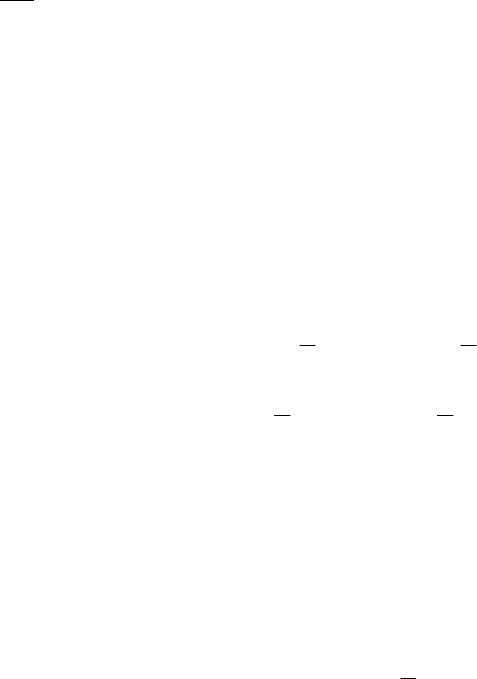
210
Это и есть уравнение распространения упругих гармонических коле-
баний части среды вдоль координаты x, фронт которых имеет вид
плоскости. Отсюда название – уравнение плоских волн.
Для полного определения распространения колебаний необходимо
задать начальные и граничные условия. Начальные условия характери-
зуют состояние колеблющегося источника в начальный момент време-
ни, т.е. при t = 0.
U
x
U
x
(,) ()0 = – смещение частиц среды,
∂
∂
ϕ
U
t
x= ()
– скорость смещения в начальный момент времени t.
Граничные условия показывают характер волнового колебания на
границах вдоль оси x, т.е. при x = 0 и x = l:
Ut
Ult t
(,)
(,) ()
00=
=
ϕ
.
Совокупность начальных и граничных условий называется также крае-
выми условиями. Уравнение (VIII.21) представляет собой линейное
дифференциальное уравнение 2-го порядка. Его общее решение имеет
вид:
, sincos
sincos
++
++
+
−+
−=
c
x
tiB
c
x
tB
c
x
tiA
c
x
tAU
ωω
ωω
(VIII.22)
где A и B – постоянные интегрирования, зависящие от краевых усло-
вий. Первые два слагаемых в правой части уравнения (VIII.22) выра-
жают плоскую волну, распространяющуюся в положительном направ-
лении оси x, вторые два выражают обратную, т.е. отраженную от гра-
ницы l, волну, возвращающуюся к источнику (рис. 58). В безграничной
среде отраженной волны не будет, т.е. уравнение примет вид:
UA t
x
c
=−
cos
ω
, (VIII.23)
где А характеризует амплитуду смещения U в точке x = 0, т.е. ампли-
туду источника возбуждения. Колебания частиц среды вдоль оси x
создаются движением бесконечной плоскости, перпендикулярной на-
правлению распространения волны.

211
Рис. 58. Образование прямой и отраженной волн в океане:
U
I
1
– отраженная от дна; U
2
– отраженная от поверхности акустического
фундамента; U
II
1
– двухкратно отраженная от дна волна
§3. Акустическое давление и колебательная
скорость плоской волны
Введение понятия звукового потенциала U позволяет определить
ряд важных параметров плоской волны. Потенциал U в безграничной
среде определяется выражением:
UA t
x
c
=−
cos .
ω
(VIII.24)
Производная потенциала U по времени, умноженная на плотность
среды ρ, характеризует акустическое давление P плоской волны:
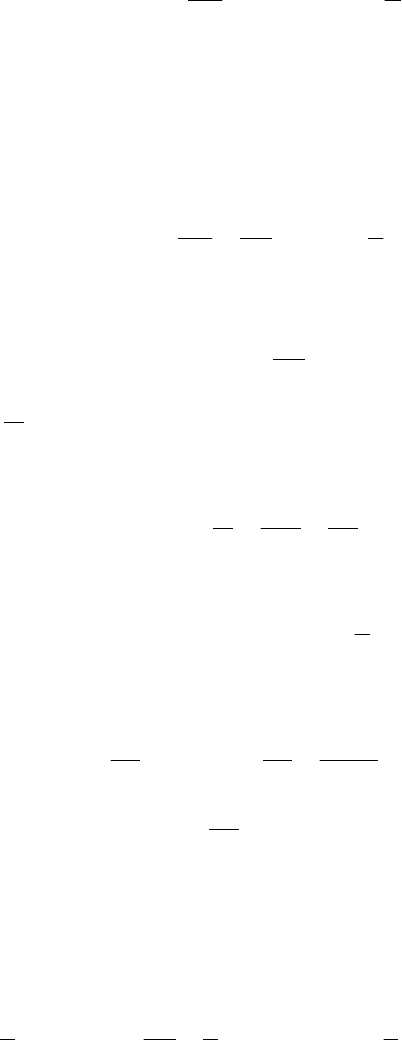
212
−=−=
c
x
tA
t
U
P
ωρω
∂
∂
ρ
sin
. (VIII.25)
Амплитуда акустического давления P
m
равна:
PA
m
=
ρω
. (VIII.26)
Производная потенциала U по направлению x определяет колеба-
тельную скорость плоской волны:
V
U
x
A
c
t
x
c
=− = −
∂
∂
ω
ω
sin . (VIII.27)
Амплитуда колебательной скорости V
m
равна:
V
A
c
m
=
ω
. (VIII.28)
Величина
ω
c
k= называется волновым числом, показывающим, сколь-
ко длин волн
λ
укладывается на расстоянии x = 2
π
, т.е.
k
c
f
c
== =
ω
π
π
λ
22
. (VIII.29)
Сравнивая выражения (VIII.25) и (VIII.27), видим, что под знаком
синуса стоит одно и то же выражение
ω
t
x
c
−
. Это значит, что в пло-
ской волне акустическое давление P и колебательная скорость V рас-
пространяются синфазно.
Взяв отношение
P
V
m
m
, получим:
P
V
Ac
A
c
m
m
==
ρω
ω
ρ
; таким образом,
P
V
c
m
m
==
ργ
. (VIII.30)
Полученное выражение называется акустическим сопротивлением
(импедансом) среды.
Интенсивность I акустических колебаний плоской волны опреде-
ляется из соотношения:
IPV A
A
c
kA
mm
== =
1
2
1
2
2
ρω
ω
ρω
, т.е. IkA=
1
2
2
ρω
. (VIII.31)

213
Выражения (VIII.26), (VIII.28) и (VIII.31) показывают, что амплитуды
акустического давления, колебательной скорости и интенсивности
плоской волны не зависят от расстояния x, т.е. плоская волна в одно-
родной непоглощающей среде распространяется без потерь. Это объ-
ясняется тем, что при постоянной скорости и бесконечной длине фрон-
та волновые поверхности при удалении от источника колебаний не
увеличиваются.
В реальных средах при возбуждении упругих колебаний в воде
или в твердых породах интенсивность акустических колебаний по мере
удаления от источника возбуждения уменьшается. Это ослабление ин-
тенсивности вызвано главным образом геометрическим расхождением,
т.е. увеличением фронта волновой поверхности при удалении от ис-
точника и рассеянием энергии ударного импульса на мелкомасштаб-
ных, соизмеримых с длиной волны неоднородностях среды. При нали-
чии границ раздела энергия уменьшается также за счет частичного от-
ражения волн от этих границ.
Рассеяние энергии акустического излучения за счет превращения
ее в тепло обычно не принимается в расчет ввиду слабого влияния это-
го фактора на величину поглощения. Таким образом, движение аку-
стической волны в реальных средах рассматривается как адиабатиче-
ский процесс, т.е. процесс, не сопровождающийся теплопередачей.
Уравнение плоской волны с учетом поглощения морской воды
имеет вид:
tx
U
x
U
c
t
U
3
4
2
3
2
2
2
2
2
∂∂
∂
ρ
µ
∂
∂
∂
∂
⋅⋅+= . (VIII.32)
Здесь
µ
– коэффициент сдвиговой вязкости, зависящий от температуры
и солености морской воды. Он уменьшается с увеличением температу-
ры и увеличивается с увеличением солености. Последний член в пра-
вой части уравнения (VIII.32) и определяет поглощающие свойства
среды.
Вещественная часть этого уравнения имеет вид:
UAe t
x
c
x
=−
−
α
ω
cos , (VIII.33)
где А – амплитуда колебаний источника в начальный период времени
t=0, α – коэффициент поглощения, измеряемый в неперах, или в об-
ратных единицах длины, или в децибелах и имеющий размерность
(см
-1
). При этом

214
1нп/см = 8,686 дб/км. (VIII.34).
Согласно Стоксу, коэффициент поглощения по амплитуде равен:
α
πµ
ρ
==
8
3
22
2
2
f
a
Af . (VIII.35)
Отсюда видно, что поглощение пропорционально квадрату частоты и
коэффициенту вязкости среды
µ
. Последний измеряется в пуазах и
имеет размерность г/см⋅с.
Из формулы (VIII.33) можно заключить, что амплитуда акустиче-
ских колебаний плоской волны уменьшается с расстоянием x по экспо-
ненциальному закону e
x−
α
.
В соответствии с полученным выражением (VIII.33) формулы для
амплитуд акустического давления, колебательной скорости и интен-
сивности для поглощающей среды примут вид:
PAe
V
A
c
e
IkAe
m
x
m
x
x
=
=
=
−
−
−
ρω
ω
ρω
α
α
α
1
2
2
, (VIII.36)
Таким образом, плоская волна в поглощающей среде будет характери-
зоваться затуханием пропорционально члену e
x−
α
.
Анализ формулы Стокса (VIII.35) показывает, что поглощение
увеличивается с увеличением частоты колебаний. В сейсмическом
диапазоне частот, т.е. при f = 5÷1000 гц, коэффициент поглощения в
морской воде близок к нулю.
В твердых средах он зависит от плотности, пористости и размеров
зерен породы. Например, в осадочных породах α выше, чем в кристал-
лических (базальтовых, гранитных). При этом величина коэффициента
поглощения на высоких частотах обусловлена главным образом тек-
стурными неоднородностями пород (пористостью, размером зерен,
тонкой слоистостью и т.д.). На низких частотах α зависит от крупно-
масштабных неоднородностей разреза.
В морской воде поглощение наиболее ощутимо для высокочастот-
ных колебаний (порядка десятка килогерц). Оно обусловлено вязко-
стью воды, а также насыщенностью воды микроэлементами органиче-

215
ского и неорганического происхождения (фито- и зоопланктон, взвесь,
пузырьки воздуха и т.д.).
Теоретический коэффициент поглощения для чистой пресной воды
в децибелах на км равен:
α = 7,4 ⋅ 10
-11
f
2
, (VIII.37)
т.е. коэффициент поглощения растет пропорционально квадрату часто-
ты. Это весьма важный вывод, на котором основан выбор частоты из-
мерения гидроакустических систем.
На основе изучения распространения волн от атомных взрывов для
частот от 16 Гц до 60 кГц для коэффициента поглощения в морской
воде получена следующая эмпирическая формула:
кмдБf /036,0
2
3
=
α
, (VIII.38)
где f – частота в кГц.
С учетом поглощения интенсивность акустических колебаний в
морской воде определяется из следующего выражения:
x
II
1,0
0
10
−
⋅= , (VIII.39)
где I
0
– интенсивность в источнике, I – интенсивность на расстоянии x
от источника.
§4. Акустическое давление и колебательная
скорость сферической волны
Колебательная скорость и акустическое давление сферической
волны определяются так же, как и для плоской волны.
Найдем колебательную скорость прямой волны:
.cossinsin
coscos
2
2
−−
−=
−+
+
−−=
−==
c
r
t
r
A
c
r
t
rc
A
c
r
t
rc
A
c
r
t
r
A
c
r
t
r
A
rr
U
V
ωω
ω
ω
ω
ωω
∂
∂
∂
∂
(VIII.40)
Полученное выражение показывает, что амплитуда колебательной ско-
рости в сферической волне в отличие от плоской волны имеет две со-
ставляющие –
A
rc
ω
и
A
r
2
, первая из которых убывает обратно пропор-
