Онищенко Г.Б. и др. Автоматизированный электропривод промышленных установок

Подождите немного. Документ загружается.

Число колебаний w. равно числу переходов регулируемой

рдннаты через установившееся значение за время переходнр-

щесса t

Иногда при опенке динамических свойств систем электро-

вода могут использоваться дополнительные показатели.

В отдельных случаях для оценки динамических свойств сис-

ы регулирования используют интегральные оценки качества,

вная идея, Заложенная в таких оценках, состоит в том, чтобы

гризовать процесс регулирования одним числом, по велн-

е которого можно было бы сделать определенные выводы о

;кании переходного процесса в течение заданного интервала

ени. Подобного вида оценки называются функционалами

ства. Они записываются в виде

= \F{fit))dt.

Из этого выражения следует, что численное значение J

оп-

]еляется видом функции Г, характером протекания во времени

»емого параметра /('() и интервалом времени протекания пе-

>дного процесса [0.1] В качестве изучаемого парамсфа f(t)

и определении интегральных оценок Л обычно используется

дная составляющая переходного процесса, определяемая из

ошення

где: Y

<tl

(f) - свободная составляющая;

- установившееся значение регулируемого параметра;

Y(l) - переходный процесс изменения изучаемого параметра

Свободная составляющая Y

Jt) но существу представляет со-

ошибку системы регулирования во время переходного про-

са.

На

рис.

14.6 показан типичный график переходного процесса

t) и его свободной составляющей Y„(t) Для идеальной системы

/лирования Yfr(t)=0, то есть идеальная система представляет

"ой пропорциональное динамическое звено с передаточной

кцией - %

•

Поэтому, чем меньше величина Jo,

м ближе система регулирования к идеальной.

Наиболее часто используется простая квадратичная ннте-

1ьная оценка свободной составляющей вида

J, = •

Чем меньше буди i

сумма абсолютных во

лнчнн гшошадей между

Y\{t) и осью времени

на рис. 14.6, тем меньше

будет величина J, и тем

выше будет быстродейс-

твие системы регулиро-

вания. Однако при этом

перерегулирование и

число колебаний могут

быть достаточно боль-

РйсН

6. Графики перехойного

npouccci-Yw

шим

«- *ТЬ простая

«о

ембодноп

составлмюшеяY

<t) квадратичная оценка не

несет в себе достаточ

ной информации о качестве процесса регулирования.

Для того, чтобы иметь более точную характеристику* дина-

мических свойств системы в подынтетральное выражение квад-

РШг

ратичнон оценки вводят слагаемое i —--- . учитывающее квад-

V )

рат скорости протекания переходного процесса. В результате

комбинированная квадратичная интегральная оценка будет опре-

деляться соотношением

Лх =

|И«+г

к'-

где

< г - постоянная времени оптимальной экспо

6 3

ненты;

tnr ~ требуемое время переходного процесса.

Этот интеграл преобразуется к виду

d/ + rv?m

Комбинированная квадратичная оценка будет достигать ми-

нимального значения, равного

Л, =^,(0). "

если переходный процесс будет близок к оптимальной экспонен-

те с постоянной времени г.

14.5. Статические характеристики электропривода с

замкнутой по скорости системой управления

Функциональная схема электропривода постоянного тока по

Kicml- ТП-Д с обратной связью по скорости приведена па

р.

1-1.7

Уравнение механических характеристик для этой сис-

ы по аналогии с (6.11) будет:

М E

/|1И

/геи». / tufoc

где: (On, - скорое

ь холостого хода в замкнутой системе ре-

агирования;

- жесткость механических характеристик в замкнутой

:ме управления;

К-э.д.с. преобразователя, пи тающего якорную цепь двигателя.

Р) Сеть

Как было по-

казано в §5.1. в

системах управле-

ния с отрица-

тельной обратной

связью по скорос-

ти жесткость ме-

ханических харак-

теристик fi

Muy

уве-

личивается по

сравнению с жест-

костью харакгери-

в разомкнутой системе /? в (J • К) раз (см.5.8), где К - коэф-

Ащнент усиления разомкнутой системы. Для рассматриваемой

ы этот коэффициент будет

'V 7

Функциональна*

схема снс(Смм ТН-Дс

oipitua-

1С11Ы1иП

обрати

сшимо ПО

скорости

_ *>«*«.

Здесь

-коэффициентусиления усилителя;

= - ' - коэффициент усиления преобразователя;

и.

(14-2)

к. =——-

коэффициент обратной связи по скорости;

(О

С=кФ- машинная постоянная (см.6.6).

Электропривод по рассматриваемой схеме описывается сле-

шей системой уравнений

tiy u

Srf -

nUy

- К..0)

Ej = С со* I

(14.3)

*«f

М = С'1

Решая уравнения (14.1) и (14.3) с учетом (14.2) относительно

(у, получим выражение для механических характеристик привода

в замкнутой системе

со

= —

. (14.4)

C(l^tf) /?(1+Я)

Механические характеристики и принцип их формирования

в замкнутой по скорости системе управления представлена на

рис.5.5. Из (14.4) следует, что для увеличения жесткости механи-

ческих характеристик нужно увеличивать коэффициент усилении

к\ что может достигаться увеличением коэффициента усилителя

. Прн лг

(

—>ог механические характеристики привода будут аб-

солютно жесткими (/?

JJ4(

'X?) и их уравнение будет со

—

При конечных значениях var жест кость механических ха-

рактеристик замкнутой системы будет определяться величиной

Обычно по условиям эксплуатации технологических устано-

вок необходимо ограничивать максимальный момент, развивае-

мый двигатс-

Сстъ

лсм, на уровне

(2-3 Ж С этой

целью в замкну-

тых системах

электропривода

применяется за-

держанная отри-

цательная об-

ратная ешь по

гоку якоря, на-

зываемая токо-

вой отсечкой. Функциональная схема электропривода постоянно-

го тока с отрицательной обратной связью по скорости и токовой

отсечкой приведена на рис. 14.8. Токовая отсечка в этой схеме

224

Рйс И S Функциональная схема системы ТП-Д с итринв-

гсиммй обратной связью но старости и отссчкнй потоку

изована на стабилитронах VS1 и VS2. Уравнения цепи об-

ой связи по току будет:

0. если |/J

]

>тк

ШС

- ток якоря, при превышении которого вступает в дейст-

отрицательная обратная связь по току.

В результате соамест-

действия отрицатель-

обратных связей по

ти и току форми-

я механическая ха-

ристика (ext.рис. 14.9),

рая состоит из двух

сов: рабочего (I) с

кой жесткостью и

тка (2) ограничения

ента. На рабочем учас-

покя не действует от-

гельная обратная связь

току, механические ха-

фистики описываются

нением (14.4)

11ри

Рис I4.Q Мсчапичеснлс чаранерт тики систе-

мы ТП-Д с отрицательной обратной связью по

скорости к отсечкой по току

<с

работа электропривода может бы ть

Пеана следующими уравнениями

= и

-к

0-(1,-]

т1

)к у

" tc ".пс У ост

Ej = КуК„и

Е,=С(о + ГЯ

(14.6)

М -

С1

В результате решения этой системы уравнений относительно

с учетом (14.2) получим уравнение механической характерн-

ей для второго участка

*>«„*гМ** я^ +K

K.hу м

С(\

К) С

К)

\ +

К С

11ервые два слагаемых уравнения (14.7) Определяют скорость

1Ьного холостого хода механической характеристики для

)рОГО участка

со

I А(о

о:

Жесткость механической характеристики на втором участке

/дет

г шин 2 ri

"<,„

+ К,К

К,

ЙЦ у п 01 J

Если к

—>

оо, то жесткость механической характеристик на

втором участке будет р

= £., т.е. предельная жесткость

мг

механической характеристики зависит от соотношения коэффи-

циентов обратных связей к/и к

Э.д.с. преобразователя £,/ при работе двигателя с замкнутой

системой управления не остается постоянной, а изменяется в со-

ответствии с уравнением

EJ =

С<О

+ ——-М

•

На рабочем участке механической характеристики скорость

примерно постоянна. С увеличением нагрузки на валу двигателя

Ej возрастает, как показано на рис.

14.9.

После перехода на второй

участок скорость снижается до нуля, наступает режим стопоре-

М ,

ния и ^уменьшается до величины £ = — •

. Таким образом, для формирования желаемой механической

характеристики преобразователь должен иметь необходимый за-

пас по величине E

в соответствии с соотношением

Р'ичшк ~ Са>„ + I

от

Ш1

•

В этой случае жесткость верхней механической характери-

стики

Д,

ат

будет постоянной при всех нагрузках вплоть до М

отс

14.6. Многоконтурные системы с подчиненным регули-

рованием координат электропривода

Для решения задач синтеза замкнутых систем электроприво-

да, обладающих хорошим быстродействием и желаемым харак-

тером переходных процессов, разработан инженерный метод

синтеза, получивший название метода последовательной коррек-

ции с подчиненным регулированием координат или сокращенно

метод подчиненного регулирования. В основе этого метода лежит

разработка многоконтурных систем, когда в результате ^нтеза

каждый из контуров описывается передаточной функцией второ-

го или третьего порядка и обеспечивает оптимальное управление

своей выходной регулируемой координатой.

Для построения такой системы в структурной схеме силовой

Цп электропривода выделяют последовательность динамиче-

их звеньев, каждое из которых имеет на своем выходе соответ-

ующую регулируемую координату

ток (Г), скорость (со), угол

"ворота (ср) или путь (s). После этого синтезируют контуры ре-

лирования, начиная с контура тока - первой внутренней коор-

наты. Синтез обычно выполняется с использованием активных

1едовательных корректирующих звеньев (регуляторов), рев-

изуемых на операционных усилителях постоянного тока с

1Ьшим коэффициентом усиления.

В состав каждого контура входит объект регулирования с

даточной функцией W(p)„

, апериодическое звено с малой

гоянной времени W(p)^ и регулятор W(р)^,.. В результате об-

Зуется многоконтурная (2

или Законтурная) система подчи-

нного регулирования, построенная по иерархическому принци-

как показано на рис. 14.10.

W(pW. [У»

Йер>ый контур I I

* Н Koinyp тока

Второй контур

Третий контур

Контур скиростм

Контур положения

Рис 14 10 Трехконтурная система электропривода с подчиненным регулированием

/, со, if - регулируемые координаты,

f\,fi,fi

- возмущения

14.7. Принципы оптимизации в системах подчиненного

регулирования

При синтезе контуров регулирования используется два типа

гимальных настроек: настройка на модульный оптимум (МО) и

встройка на симметричный оптимум (СО). Выбор типа настрой-

ки определяется требованиями к статическим и динамическим

арактернстикам при отработке управляющих воздействий и

[возмущений, действующих внутри когпура регулирования.

Модульный оптимум настройки контуров регулирования

Считается, что замкттый контур регулирования с единич-

ной обратной связью настроен на модульный оптимум, если он

имеет передаточную функцию второго порядка вида

W{p)

o= .

:" , т. (М.8)

a^p'+a^p

l 2Т~р

2Т

где:

од/ -

коэффициент настройки на модульный оптимум;

- малая постоянная времени некомпснснруемого аперио-

дического звена;

4 - коэффициент модульной настройки;

К(

=2 • стандартный коэффициент настройки контура.

Эту передаточную функцию можно записать в форме, соот-

ветствующей колебательному звену

v 1 / (№)

(D\ <д

где: Т

= Т

- эквивалентная постоянная времени ко-

лебательного звена;

=— - частота недемпфируемых колебаний;

к гтл

/о

£ = ' коэффициент демпфирования колебаний.

Для стандартной настройки T

- T^-Jl.

= ~. определяет-

ся соотношением

= • (14.10)

Следовательно, с возрастанием коэффициента демпфирова-

ния действительная частота колебаний в контуре регулирования

уменьшается. При стандартной настройке на МО, когда а

=2,

= (14.11)

переходный процесс отработки ступенчатого задающего воздей-

ствия представлен на рис. 14.11. Он описывается уравнением

>(/)= \-е

гт

* cos— - + sin— . (14.12)

27; 27;

Действительная частота колебаний звена второго порядка и

имеет следующие показатели качества: время переходного про-

цесса = 8.47;; время нарастания /

=4.77;; время первого

максимума t^. =6.3Т

\ перерегулирование а = 4.3%; чийНо ко-

лебаний я, = I.

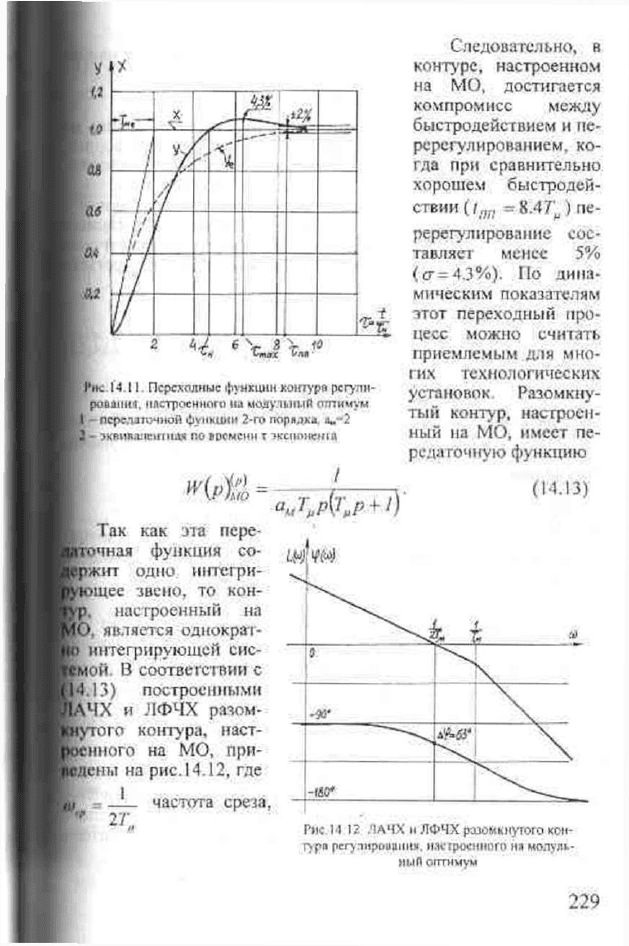
J'lIC 14.11. Переходные функции контуре регули-

рования, настроенного ни модульный оптимум

•^передаточной функции 2-го порядки. tu.--2

эквийапетшм по времени т экспоиеша

НрП -

Следовательно, в

контуре, настроенном

на МО, достигается

компромисс между

быстродействием и пе-

ререгулированием. ко-

гда при сравнительно

хорошем быстродей-

ствии (1

„ =8.47; Пе-

ререгулирование сос-

тавляет менее 5%

(сг=4.3%). По дина-

мическим показателям

этот переходный про-

цесс можно считать

приемлемым .для мно-

гих технологических

установок Разомкну-

тый контур, настроен-

ный на МО, имеет пе-

редаточную функцию

(14.13)

Так как эта пере-

чная функция со-

жнт одно интегри-

щее звено, то кон-

настроенный на

JO, является однократ-

интегрирующей сис-

йой. В соответствии с

34,-13) построенными

1ЛЧХ и ЛФЧХ разом-

того контура, наст-

енного на МО, при-

цепы на рис. 14.12, где

_!_ частота среза,

2 Г.

Рис.

12 ЛАЧХ н ЛФЧХ разойкнугого кон-

тора регулировании. nacipooHiwrn ня молуль-

иыП оптимум

о) - J— - частота сопряжения асимптот, а запас по фазе на час-

' Т.

тоте среза

A<p

c/i

= 180°-

<р

ср

= 63°.

Таким образом, задачей синтеза контура при настройке на

МО является выбор регулятора - последовательного коррек-

тирующего звена с такой передаточной функцией, чтобы разомк-

нутый контур имел передаточную функцию (14.13).

Симметричный оптимум настройки контуров регулирования

Считается, что замкнутый контур регулирования с единич-

ной отрицательной обратной связью настроен на симметричный

оптимум (СО), если он имеет передаточную функцию третьего

порядка вида

, , 4Т

р +1

™\Р)со

, at 7

р +4T

\ (И. 14)

47> +

8Г„У+87;V+47> + l

где: а

- коэффициент настройки на симметричный оптимум;

7^ - малая постоянная времени некомпенсируемого

апериодического звена;

=3,5-^-8 - коэффициент симметричной настройки;

=8 - стандартный коэффициент настройки контура.

Для контура, имеющего стандартную настройку на СО

(я

=8), переходный процесс отработки ступенчатого задающего

воздействия дан на рис. 14.13. Он описывается уравнением

'Л

И'Н

+ е

2е *

cos

v -

(14.15)

и имеет следующие показатели качества: время переходного про-

цесса t

= 16.5T

\ время нарастания t

=3.1 Г

;

время 1-ого мак-

симума t

vaKC

=5.87^; время 1-ого минимума /^ = 12.757),;

перерегулирование а - 43%; число колебаний n

= 2 .

Из анализа показателей качества следует, что они в значи-

тельной степени отличаются от показателей контура, настроенно-

го на МО. Большое перерегулирование, равное сг=43%, обуслов-

лено влиянием форсирующего звена fV(p)=4Tp+1 в числителе

передаточной функции (14.14).