Обработка материалов давлением: сборник научных трудов. Вып. №20

Подождите немного. Документ загружается.

Обработка материалов давлением № 1 (20), 2009

0 0.4 0.8 1.2

ain

120

160

ess, MPa

Point0

Point1

Point2

012345

time, s

120

160

stress, MPa

Point0

Point1

Point2

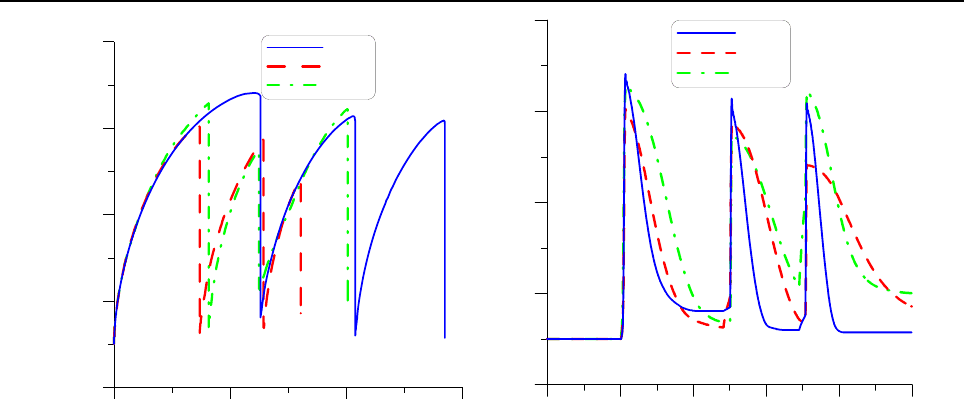
Рис. 8. Изменение напряжения текучести в процессе прокатки

ВЫВОДЫ

В статье представлены результаты моделирования изменения микроструктуры с по-

мощью клеточных автоматов. Модель ориентирована на создание начальной структуры

и моделирования процесса деформации с рекристаллизацией. При моделировании учиты-

вается деформация путем измениния размеров и формы клеток. Результаты, представлен-

ные в работе, показывают возможности клеточных автоматов по предсказанию микрострук-

туры, позволяют определить

размеры зерна и характер процесса рекристаллизации.

Работа проводится в рамках проектов № №

N508 002 32 / 0158 и N 508 3812 33,

фи-

нансируемых Министерством Науки и Высшего Образования Польши в 2006–2010 годах

ЛИТЕРАТУРА

1. Weygand D., Brechet Y., Lepinoux J. // Adv. Engng. Mater. – 2001. – № 3. – Р. 67–71.

2. Fan D., Chen L. Q. // Acta Mat. – 1997. – № 44. – Р. 611–622.

3. Holm E. A., Hassold G. N., Miodownik M. A. // Acta Mat. – 2001. – № 49. – Р. 2981–2991.

4. Bernacki M., Chastel Y., Digonnet H., Resk H., Coupez T., Loge R. E. // Comp. Meth. .Mat. Sci. – 2007. –

№ 7. – Р. 42–149.

5. Davies C. H. J. // Scr. Mater. – 1997. – № 36. – Р. 35–40.

6. Three-dimensional cellular automata for simulation of microstructure evolution, Proc. Conf COMPLAS IX , eds. /

Svyetlichnyy D., Oñate E., Owen R., Suárez B. – Barcelona, 2007. – Р. 983–986.

7. Qian M., Guo Z. X. // Mater. Sci. Eng. – A, 2004. – Р. 180–185.

8. Svyetlichnyy D. // Comp. Meth. .Mat. Sci. – 2009. – № 9 ( в печати).

9. Makarov P. V., Romanova V. A. // Teor. Appl. Fract. Mech. – 2000. – № 37. – Р. 1–7.

10. Svyetlichnyy D. Steel and Related Mat. // Steel Crips. – 2008. – № 79, v. 2. – Р. 452–458.

11. Светличный Д.С. // Системнi технологii. – 2008. – № 47–56. – С. 42–47.

12. Svyetlichnyy D. S. «Consideration of Deformation during the Automata Cellular Simulation», in Nowe

Technologie i osiągnięcia w metalurgii i inżynierii materiałowej / Svyetlichnyy D. S., Dyja H., Szecówka L. //

Conference Proceedings. – Cz

ęstochowa, 2006. – Р. 533–536 (in Polish).

13. Миленин А. А. Исследование численных свойств алгоритмов метода конечных элементов

применительно к трехмерным задачам обработки металлов давлением / А. А. Миленин // Изв. РАН. Металлы. –

1998.– № 5.– С. 33–37.

14. Миленин А. А. Проблемы разработки и применения трехмерных численных моделей для оптимизации

процессов прокатки / А. А. Миленин // Сучасні проблеми металургії. Наукові

вісті. Том. 5. Пластична

деформація металів. – Дніпропетровськ: «Системні технології». – 2002. – С.36–46.

Светличный Д. С. – д-р техн. наук, проф. КГМА;

Миленин А. А. – д-р техн. наук, проф. КГМА.

КГМА – Краковская горно-металлургическая академия (AGH), г. Краков, Польша.

E-mail: milenin@metal.agh.edu.pl

110

Обработка материалов давлением № 1 (20), 2009

УДК 621.771.01

Сатонин А. В.

Михеенко Д. Ю.

Иванов А. А.

ВАРИАЦИОННОЕ МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДЕФОРМИРОВАННОГО

СОСТОЯНИЯ МЕТАЛЛА ПРИ ПРОКАТКЕ С ЗАТЕКАНИЕМ В ЩЕЛЕВОЙ ПАЗ

Решению задач по экономии материальных ресурсов, а также по расширению сор-

тамента и повышению качества готовой металлопродукции в значительной степени спо-

собствует увеличение объемов производства различных металлоизделий со сложной фор-

мой поперечного сечения которые представляют собой готовую продукцию не требующую

дальнейшей механообработки. К такой продукции можно отнести листы с односторонним

оребрением.

Прокатку таких листов и деталей, или, как часто ее именуют, контурную прокатку,

можно разделить на два основных вида:

• прокатку между гладким валком и подвижным штампом с нанесенном на по-

следнем заданной гравюры

• прокатка между двумя валками, из которых один гладкий, а другой имеет тре-

буемую гравюру.

В первом случае можно получать различную конфигурацию детали, длинна которой

ограничена рабочей длинной штампа, во втором длинна изделия может быть неограничен-

ной, однако контур должен быт постоянным по длине или повторятся на участке, равном

длине окружности гравированного валка.

Целью данной статьи является математическое моделирование процесса получения

листов с односторонним оребрением с помощью затекания металла в пазы гравированного

валка.

Основным допущением при анализе напряженно-деформированного состояния ме-

талла в существующих моделях на основе конечно-разностного подхода, метода полей ли-

ний скольжения и метода конечных элементов является отсутствие учета продольного пла-

стического формоизменения металла [1] и, в частности, влияет на выбор исходной длины

заготовки, определяющей объем последующей обрези и, как следствие, коэффициент вы-

хода годной металлопродукции.

В соответствии с рекомендациями работ [2–3] трехмерное математическое моде-

лирование напряженно-деформированного состояния металла при прокатке с

затеканием

в продольные пазы рабочего инструмента было выполнено на основе вариационных под-

ходов, предполагающих определение минимума суммарной мощности пластического

формоизменения. Используемая в этом случае расчетная схема участка пластического

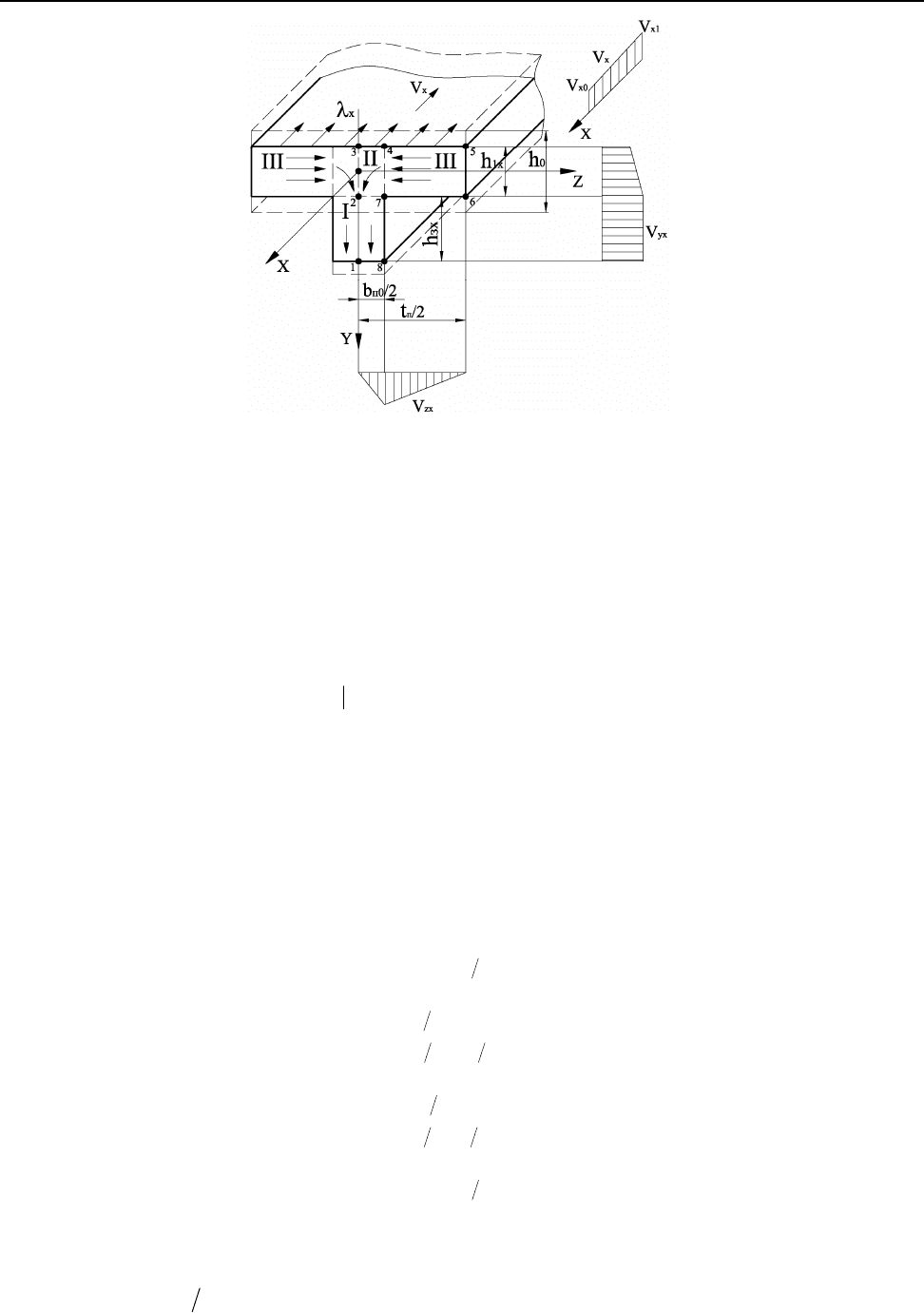
формоизменения металла представлена на рис. 1.

Рассматривая участок деформируемого металла в рамках одной щелевой полости,

а в следствии его симметрии - только одну его правую

половину, выделим по аналогии

с методикой работы [2] три зоны, а именно (см. рис. 1):

• зону I, ограниченную по периметру отрезками 1278, в которой металл течет вдоль

осей

заполняя тем самым щелевую полость;

• зону II, ограниченную отрезками 2347, в которой металл течет вдоль оси

обжимается по оси

и перетекает по оси

в щелевую полость;

• зону III, ограниченную отрезками 4567, в которой металл заготовки обжимается по

оси

, а также течет в продольно по оси

и в поперечном по оси

направлениях, при

этом по оси

пластическое течение металла осуществляется только в сторону щелевого

паза поскольку граничное сечение 56 сопряжено с аналогичным сечением соседнего паза

с аналогичной геометрией.

111

Обработка материалов давлением № 1 (20), 2009

Рис. 1. Расчетная схема поперечного сечения очага деформации при прокатке с затеканием

в продольные пазы рабочего инструмента

Помимо указанного выше в рамках разрабатываемой вариационной математической мо-

дели был принят еще ряд допущений, основными как и в случае реализации вариационного под-

хода применительно к прокатке сложных профилей [3], являются следующие:

• скорости продольного

течения металла вдоль оси

для всех трех участков, исходя из

условия сохранения сплошности эквивалентны, то есть:

xxIIIxIIxI

VVVV

; (1)

• скорости перемещения прокатываемой составляющей в последнем сечении зоны пла-

стического формоизменения

VV равна окружной скорости верхнего рабочего валка

V ;

• утяжкой металла в щелевой полости по ширине, то есть поперечной деформацией по

оси

в зоне I вследствие ее малого значения пренебрегаем;

• текущие значение сопротивления сдвигу металла, а также коэффициенты пластическо-

го трения на контактных поверхностях верхнего рабочего валка всем объеме очага деформации

являются величинами постоянными и равными их усредненным значениям

K и

μ , соответ-

ственно.

С учетом характера принятых допущений и по аналогии с методиками работ [1–3] мощ-

ности внутренних сил для каждого из рассматриваемых зон очага деформации (см. рис. 1) могут

быть определены как:

∫∫ ∫

IcвсI

dxdydzHKN

; (2)

∫∫ ∫

−

IIcвсII

dxdydzHKN

; (3)

∫∫ ∫

c п

IIIcвсIII

dxdydzHKN

, (4)

где z,

- продольная, высотная и поперечная геометрические координаты принадлежащие

вертикальной плоскости симметрии всего участка одной щелевой полости (см. рис. 1), при этом

начало геометрической координаты

имеет место в плоскости выхода металла из валков;

()

hhh

+= - средняя толщина прокатываемого металла в очаге деформации;

1з

h - конечная толщина металла затекшего в щелевую полость;

пп

t,b

- ширина щелевых полостей и шаг их размещения на рабочем инструменте;

112

Обработка материалов давлением № 1 (20), 2009

H,H,H

- показатели интенсивности деформации сдвига на соответствующих уча-

стках, определяемых в строгом соответствии с методиками работ [2–3].

По аналогии с процессом прокатки тавровых профилей в ребровых калибрах [3] были

получены аналитические описания для определения и остальных составляющих суммарной

мощности всех сил сопротивления деформации, а именно:

- мощности взаимодействия участков

III,II,I

с внешней средой:

()

dydzVVKN

зп

yIcввI

∫∫

; (5)

dydzVVKN

zII

yIIcввII

∫∫

−

; (6)

()

dydzVVKN

hbt

zIII

yIIIcввIII

пп

∫∫

−

; (7)

- мощности взаимодействия участков

dxdyVVKN

yIIIyIIcIIIcII

∫∫

−

−=

; (8)

- мощность внешних сопротивлений, то есть сил внешнего контактного трения скольже-

ния на контактных поверхностях участка

()

∫∫

+−μ=

zIIIвxcIII

dxdzVVVKN

2 ; (9)

- мощность сил внешнего контактного трения скольжения на контактной поверхности

участка

и верхнего рабочего валка:

()

∫∫

+−μ=

zIIвxcII

dxdzVVVKN

2 , (10)

где

zyx

V,V,V - скорости течения металла вдоль соответствующих геометрических координат;

V - окружная скорость вращения рабочих валков.

С учетом (1)-(10) функцию полной мощности всех сопротивлений деформации можно

представить в виде:

IIIIIIIIcIIввIIIввIIввIвсIIIвсIIвсI

NNNNNNNNNN

ττ−Σ

+++= . (11)

При этом последующие решение осуществляют путем аналитического описания полей

скоростей и деформации с последующим определением варьируемых параметров, соответст-

вующих минимуму полной мощности

N или его приведенного значения

()

вc

VKNN

ΣΣ

= [3].

Следует отметить, что рассмотренное выше решение в его аналитическом виде является

весьма громоздким и требует принятия целого ряда дополнительных допущений, отрицательно

сказывающихся на степени достоверности предоставляемых результатов. В свете изложенного

представляет интерес реализации численного рекуррентного подхода, основанного на конечно-

разностном анализе мощностей всех сопротивлений деформации в рамках каждого выделенного

элементарного объема металла в зоне его пластического формоизменения. Используемые в этом

случае расчетные схемы интегрального очага деформации и выделенного

-го элементарного

объема представлены на рис. 2, при этом в качестве основных допущений использовались сле-

дующие предположения:

• пластическое течение металла в продольном направлении, то есть вдоль оси

во всех

трех зонах подчиняется гипотезе плоских сечений [4, 5], аналогичной гипотезе подчиняется и

течение металла в зоне

в поперечном направлении (вдоль оси

) и в зоне

в вертикальном

направлении (вдоль оси

);

113

Обработка материалов давлением № 1 (20), 2009

а б

Рис. 2. Расчетная схема интегрального очага деформации (а) и его выделенного

элементарного объема (б) при прокатке с затеканием в продольные пазы рабочего инструмента

• аналитическое описание текущего о длине деформации значения толщины прокаты-

ваемого металла

h соответствует степенной зависимости вида:

()

(

)

101

Lxhhhh −+= ; (12)

• аналитическое описание текущих по длине очага деформации значений коэффициентов

внешнего трения на контактных поверхностях верхнего рабочего валка

μ и прокатываемого

металла

μ соответствует степенным зависимостям вида:

(

)

101

μ=μ

Lx ;

(

)

202

μ=μ

Lx , (13)

где

μ ,

μ - опорные значения коэффициентов внешнего пластического трения на соответст-

вующих контактных поверхностях, определяемые их шероховатостями, температурой, скоро-

стью относительного скольжения и целым рядом других факторов [7, 8];

1μ

a ,

2μ

a - степенные показатели характеризующие реальную форму эпюры изменения

рассматриваемых коэффициентов;

• сопротивление сдвигу прокатываемого металла

k , коэффициенты внешнего пластиче-

ского трения

μ ,

μ и геометрические параметры

h ,

зx

h изменялись вдоль очага деформа-

ции по довольно сложным законам в рамках

-го выделенного элементарного объема изменяют-

ся линейно.

Используя в качестве аналитического описания текущего по длине очага деформации

значения толщины прокатываемого металла степенной зависимости (12) определим значения

данной толщины для начального

1xj

и конечного

2xj

граничных сечений каждого отдельного

i -го элементарного объема очага деформации (см. рис. 2):

(

)

(

)

()

,Lxhhhh

;Lxhhhh

gjxj

21012

11011

−+=

(14)

где

x ,

x - геометрические координаты начального и конечного граничных сечений выде-

ленного i -го элементарного объема, определяемые с учетом принятой схемы разбиения

(см. рис. 2) как:

krLx =Δ ;

(

)

−

Δ= jkrxx

;

(

)

jkrxxxx

jjj

−

. (15)

114

Обработка материалов давлением № 1 (20), 2009

Приняв в дальнейшем в качестве варьируемого параметра результирующие значе-

ние вытяжки прокатываемого металла

определяемое как соотношение площадей попе-

речных сечений в исходном

thF

= и в результирующем

0111 пзп

bhthF +

состояниях

и предположив, что текущие по длине очага деформации значение вытяжки

λ распреде-

ляется в соответствии с текущим значением толщины

h , определим значения вытяжки

1xj

λ и

2xj

λ , а вместе с этим и значение площадей начального

1xj

F и конечного

2xj

F гра-

ничных сечений выделенного i -го элементарного объема:

()

⎥

⎦

⎤

⎢

⎣

⎡

+−λ

⎟

⎠

⎞

⎜

⎝

⎛

λ=λ 11

;

()

⎥

⎦

⎤

⎢

⎣

⎡

+−λ

⎟

⎠

⎞

⎜

⎝

⎛

λ=λ 11

; (16)

10101 xjпxjxj

thFF

=λ= ;

20202 xjпxjxj

thFF

. (17)

С учетом известных текущих значений вытяжек

1xj

2xj

и площадей

1xj

F ,

2xj

могут быть определены и соответствующие значения скоростей продольного (вдоль оси

) течения металла

)(xIj)(xj

2121

)(xIIIj)(xIIj

2121

, а также текущие значение

толщины прокатываемого металла, находящейся в продольных пазах калиброванного

валка

1зxj

2зxj

(см. рис. 2):

1111

xjxj

VV ;

1212

xjxj

VV ; (18)

(

)

0111 ппxjxjзxj

bthFh

−

= ;

(

)

0222 ппxjxjзxj

bthFh

−

, (19)

где

V - скорость перемещения прокатываемого металла в сечении на выходе из рабочих

валков, соответствующая в силу принятых допущений окружной скорости вращения

верхнего валка и нижнего валков

V .

Усреднив расчетные согласно (18) значения скоростей

1xj

V и

2xj

V время прохож-

дения металлом каждого отдельного выделенного

i -го элементарного объема определим

как:

(

)

xjxjxj

VVxt

. (20)

Аналогично, то есть исходя из чисто геометрических и кинематических соотноше-

ний, а также закона сохранения объемов могут быть определены и другие характеристики

деформированного состояния прокатываемого металла, имеющие место в рамках каждого

отдельного

i -го элементарного объема (см. рис. 2).

В частности, приращение объема прокатываемого металла, находящейся в полости

гравированного валка, то есть в рамках зоны

определяется как:

(

)

xbhhW

пзxjзxjjI

−

012

, (21)

откуда скорость его пластического течения в заданной зоне соответствует:

(

)

(

)

xjзxjзxjxjпjIjIy

thhtxbWV

120

−

Δ= . (22)

Аналогично может быть определено и уменьшение объема металла в зоне

обу-

словленное его обжатием с толщины

1xj

h до толщины

2xj

h :

(

)

(

)

021 ппxjxjjIII

btxhhW

−

Δ , (23)

при этом объем металла деформируемого в продольном направлении, то есть вдоль оси

соответствует:

(

)

(

)

02211 ппxjxjxjxjjIIIx

btxhhW

−

=Δ

, (24)

а в поперечном направлении, то есть по оси

jIIIxjIIIjIIIz

WWW

−

, (25)

115

Обработка материалов давлением № 1 (20), 2009

откуда скорость пластического течения

zjIII

в сечении 4-7 может быть определена как:

(

)

[

]

jxxjxjjIIIzzjIII

txhhWV

− 21)74(

2 . (26)

И, наконец, среднее значение скорости пластического течения прокатываемого ме-

талла вдоль оси

для второй зоны

jIIyc

V исходя из разности приращения объемов

jII

WΔ определим как:

(

)

(

)

0пjIIIjIjIIyc

bxWWV

−

. (27)

По аналогии с кинематическими параметрами в конечно-разностном виде для каж-

дого выделенного i -го элементарного объема могут быть определены и показатели сте-

пени логарифмической деформации.

На основе реализации численного рекуррентного подхода определяются значения

составляющих полной мощности всех сопротивлений деформации (1-10):

∑

IjsвсI

HKN

; (28)

∑

IIjsвсII

HKN

; (29)

∑

IIIjsвсIII

HKN

; (30)

∑

jzI

jyIcввI

VVKN

; (31)

∑

jzII

jyIIcввII

VVKN

; (32)

∑

jzIII

jyIIIcввIII

VVKN

; (33)

∑

−

−=

jyIIIjyIIcIIIcII

VVKN

; (34)

()

∑

+−μ=

jzIIIвjxcIII

VVVKN

2 ; (35)

()

∑

+−μ=

jzIIвjxcII

VVVKN

2 . (36)

Суммарную мощность всех сопротивлений деформации определяли по формуле

(11). В целом, полученные аналитические зависимости (11)-(36) составили полный алго-

ритм по автоматизированному прогнозированию глубины затекания прокатываемого ме-

талла в пазы гравированного валка в процессе прокатки листов с односторонним оребре-

нием.

В ходе реализации предложенного решения варьировался параметр вытяжки

с целью нахождения минимума значения суммарной мощности формоизменения

N .

В качестве примера была рассмотрена задача со следующими исходными данными: ис-

ходная толщина заготовки 7

=h мм, конечная толщина 4

h мм, период паза 20

t мм,

ширина паза 5

b мм, радиусы валков 200

R мм, прокатываемый материал медь М

Результаты данных исследований представлены на рис. 3.

116

Обработка материалов давлением № 1 (20), 2009

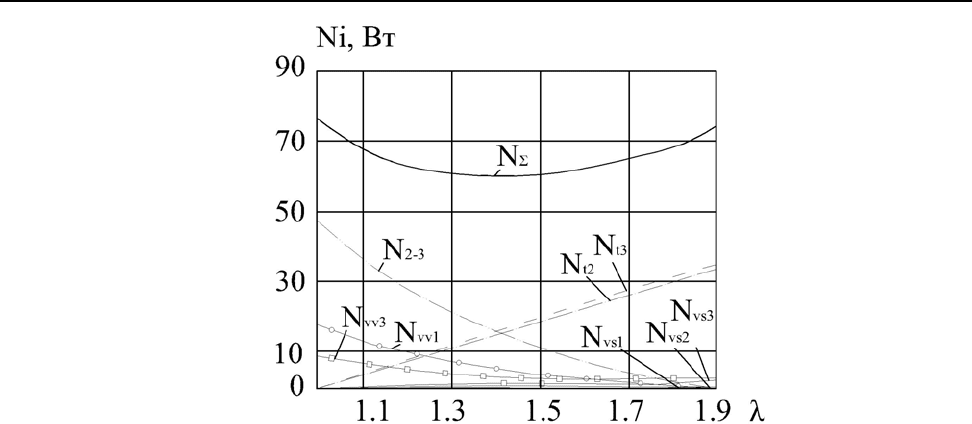
Рис. 3. Расчетные распределения зависимости составляющих полной мощности

формоизменения N

от продольной вытяжки прокатываемого металла

ВЫВОДЫ

Анализируя полученные результаты следует отметить, что суммарная мощность процес-

са не имеет ярко выраженного минимума. Минимальные значения наблюдаются в промежутке

вытяжек от 1,3 до 1,5. Таким образом с точки зрения минимальных затрат энергии формоизме-

нения основная часть металла будет стремится к вытяжке не заполняя пазы валка, что может

привести к возникновению

брака в готовом изделии. Также следует отметить, что на суммарную

мощность в большей степени влияют мощности взаимодействия участков

, а также

мощности сил внешнего контактного трения скольжения на контактных поверхностях участков

II и

, причем в случае роста мощностей

III

с одновременным снижением величины

IIIcII

−

происходит смещение минимальной мощности процесса в сторону уменьшения сум-

марной вытяжки и, как следствие, увеличение глубины заполнения пазов

ЛИТЕРАТУРА

1. Михеенко Д. Ю. Автоматизированный расчет энергосиловых параметров процесса прокатки биметал-

лической композиции с механической связью / Д. Ю. Михеенко // Удосконалення процесів і обладнання обробки тис-

ком у металургії і машинобудуванні: зб. наук. пр. – Краматорськ : ДДМА, 2004. – С. 481–484.

2. Тарновский И. Я. Теория обработки металлов давлением (Вариационные методы расчета усилий и де-

формаций) / И

. Я. Тарновский [ и др.]. – М. : Металлургия, 1963. – 672 с.

3. Тарновский И. Я. Элементы теории прокатки сложных профилей / И. Я. Тарновский, А. Н. Скороходов,

Б. М. Илюкович. – М. : Металлургия, 1972. – 352 с.

4. Прокатное производство: учебник для вузов / П. И. Полухин, Н. М. Федосов, А. А. Королев,

Ю. М. Матвеев. – 3-е изд. – М. : Металлургия, 1982. – 696 с.

5. Машины и агрегаты металлургических заводов. В 3 т. Т. 3. Машины и агрегаты для производства и от-

делки проката : учебник для вузов / А. И. Целиков [и др.]. – М. : Металлургия, 1981. – 376 с.

6. Королев А. А. Конструкция и расчет машин и механизмов прокатных станов / А. А. Королев. – М. : Ме-

таллургия, 1969. – 424 с.

7. Грудев А. П.

Внешнее трение при прокатке / А. П. Грудев. – М. : Металлургия, 1973. – 285 с.

8. Чертавских А. К. Трение и технологическая смазка при обработке металлов давлением / А. К. Чертав-

ских, В. К. Белосевич. – М. : Металлургия, 1968. – 362 с.

Сатонин А. В. – д-р техн. наук, проф. ДГМА;

Михеенко Д. Ю – канд. техн. наук ДГМА;

Иванов А. А. – аспирант ДГМА.

ДГМА - Донбасская государственная машиностроительная академия, г. Краматорск.

E-mail: amm@dgma.donetsk.ua

117

Обработка материалов давлением № 1 (20), 2009

УДК 678.029:678.053:678.027.2

Сатонин А. В.

Грибков Э. П.

Емченко Е. А.

Селедцов А. С.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ ВАЛЬЦЕВАНИЯ

И КАЛАНДРОВАНИЯ РЕЗИНОТЕХНИЧЕСКИХ ОТХОДОВ

Одной из наиболее эффективных технологий по окончательному измельчению

различного рода резинотехнических отходов, являются процессы вальцевания, а по обес-

печению возможности их вторичного использования – процессы каландрования [1, 2, 3].

При этом с точки зрения разработки математических моделей данных технологических

процессов и оценки степени их достоверности наиболее актуальным являются сопостав-

ление результатов теоретических и экспериментальных исследований при одновременном

уточнении исходных предпосылок и использовании достаточно строгих численных мето-

дов расчета.

Как следует из результатов анализа вопроса в области теоретического анализа

процессов вальцевания резинотехнических фрагментов и последующего каландрования

резиновой крошки, одним из наиболее широко используемых методов расчета являются

зависимость по определению межвалковой силы распора Рябинина и Лукача, основанная

на законах чисто упругой деформации [3, 4] и зависимость Майзеля, предполагающая,

что резиновая смесь деформируется только пластически [3, 5]. Вместе с тем, учитывая

специфику физико-механических свойств обрабатываемых материалов, механизм форми-

рования напряженно-деформированного состояния в этом случае является более слож-

ным, объединяющим в себя и упругое, и пластическое формоизменение резинотехниче-

ских фрагментов (рис. 1). В частности, в сечениях очага деформации на входе в рабочие

валки имеет место зона упругого сжатия протяженностью

упо

, необходимость учета ко-

торой обусловлена относительно малым значением модуля упругости деформируемого

материала, а также относительно высокими значениями радиусов рабочих валков

, RR

и исходной толщины

h . Вся зона упругого сжатия

упо

L в свою очередь, может быть под-

разделена на зоны свободного и стесненного сжатия, имеющие протяженности

1óïî

2упо

, соответственно (см. рис. 1). При этом в зоне свободного сжатия отдельные фраг-

менты находятся в дискретном состоянии, т.е. не контактируя друг с другом, в то время,

как в зоне стесненного сжатия данный контакт имеет место, и как следствие, имеет место

наличие нормальных осевых напряжений

С целью определения энергосиловых, кинематических и физико-механических ха-

рактеристик при реализации процесса вальцевания и каландрования была создана мате-

матическая модель, основанная на разбиении очага деформации на множество элементар-

ных объемов и анализа напряженно-деформированного состояния резинотехнической

смеси.

Одним из основных допущений, принятых в рамках данной математической модели было

допущение о том, что пластическая деформация является плоской и установившейся во

времени, при этом границы всех зон и упругого, и пластического формоизменения парал-

лельны плоскости осей вращения рабочих валков.

С целью определения текущих значений нормальных контактных р

и нормальных

осевых

напряжений рассматривалась по аналогии с традиционными схемами процесса

прокатки [6], основанные на разбиении очага деформации.

118

Обработка материалов давлением № 1 (20), 2009

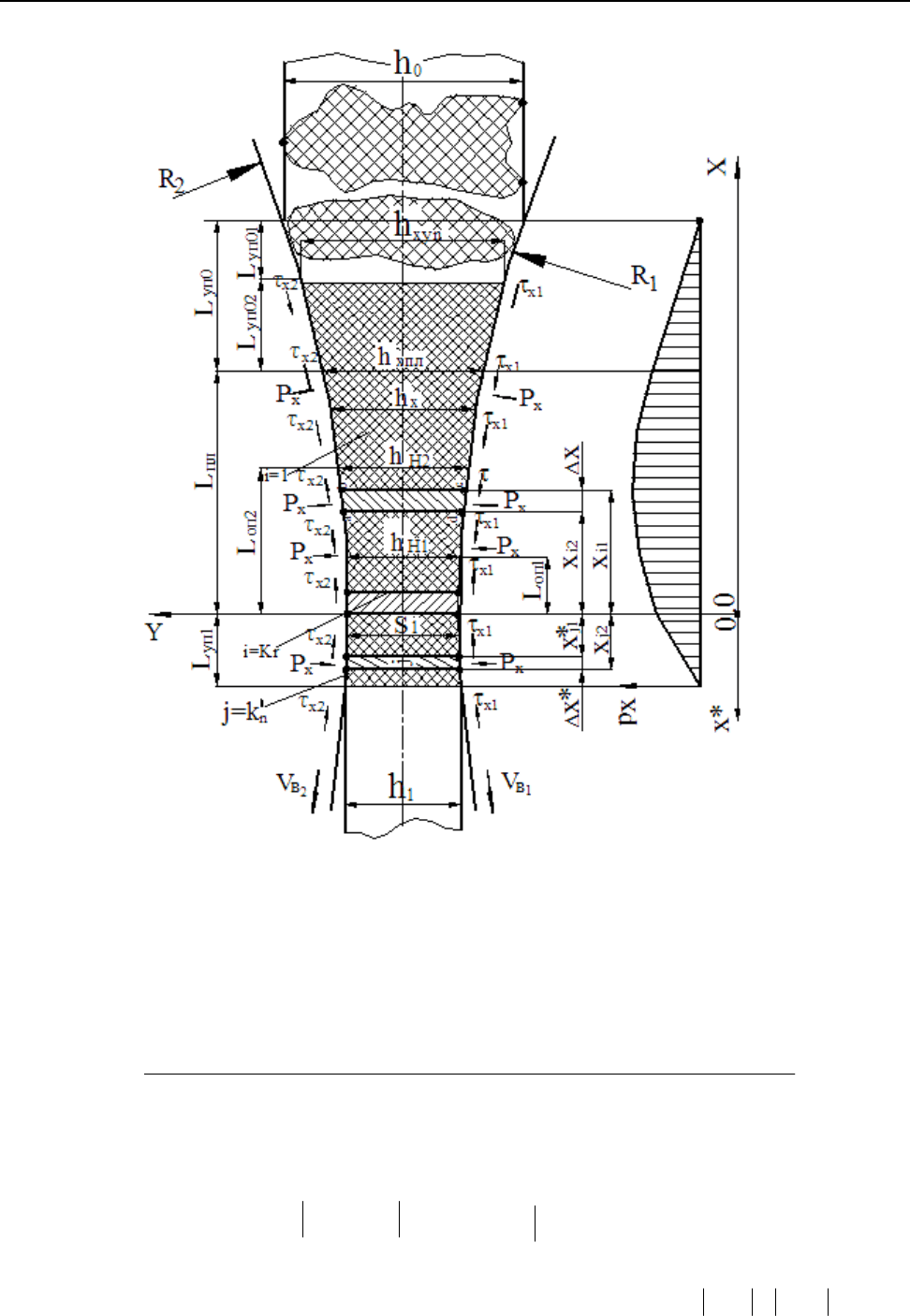
Рис. 1. Расчетная схема интегрального очага деформации применительно

к численному математическому моделированию напряженно-деформированного состояния

резинотехнических отходов при реализации процессов вальцевания и каландрования

Расчет нормальных и контактных напряжений в зоне стесненного упругого сжатия

производили по формулам:

)2/(]/)([

02022 мxiмxixi

hhhEp

−

= ; (1)

xffhh

xffhhphhhhE

ixixxiмxi

ixixxixixixixiмxixiм

Δ+−+−

Δ+

−

)()1/1(

])()[(2/)/1(

222112

121121111022

. (2)

В качестве критерия определения границы зоны стесненного упругого сжатия являет-

ся выполнение условия пластичности:

,44

xyi

xixi

iiii

≥+

⎟

⎠

⎞

⎜

⎝

⎛

−

τσ

(3)

где усредненное по высоте очага деформации значение напряжений

xyi

согласно результа-

там целого ряда исследований [7, 8] может быть определено как

()

22212 ixixxyi

τττ

+= .

По мере определения границы зоны пластического формоизменения её последующий

расчет, как и в случае зоны стесненного упругого сжатия, производили на основе численного

119