Новожилова М.В., Коюда П.М. Моделювання економічної динаміки
Подождите немного. Документ загружается.


91
випадки:
1.
Характеристичні числа
λ
1
,
λ
2
є дійсними числами,
λ
1
≠
λ
2
.
Тоді загальний розв’язок системи (2.45) у матричному вигляді набуває
вигляду:
Х(t)= С
1
X
1
+ С
2
X
2
, де еP=Х ,еP=Х
t
2
t
1
2
2
1
1
λ
λ
, (2.51)
де
Т1
2
1
1
1
)р,р(Р = – деякий власний вектор, що відповідає
λ
1
;
Т2
2
2
1
2
)р,р(Р = –
власний вектор, що відповідає довільним постійним
λ
2
, С
1
, С
2
.
2.
Характеристичні числа
λ
1
,
λ
2
…,
λ
n
є дійсними числами,
λ
1
=
λ
2
=
λ
.
Тоді корені
Х(t)= С
1
X
+ С
2
t X , де X=P
t
e
λ
(2.52)
також є коренями однорідної системи рівнянь (2.45).
3.
Характеристичні числа
λ
1
,
λ
2
є комплексно-спряженими числами:
λ
1.2
=
α
± i
β
.
Тоді загальний розв’язок однорідної системи диференціальних рівнянь (2.45)
має пару дійсних розв’язків, яку містять функції вигляду:
t
e
α
(С
1
cos (
β
t) + С
2
sin (
β
t)). (2.53)
Приклад 2.6. У результаті економічного аналізу встановлено, що поведінка
динамічної системи залежить від двох змінних
x
1
(t), x
2
(t) і описується системою
лінійних диференціальних рівнянь:
⎪
⎩
⎪
⎨
⎧
−+−=
−−=
,2xx
dt
dx
,2x2x
dt
dx
21
2
21
1
(2.54)
Необхідно:
1. дати характеристику системи (2.54);
2. знайти загальний розв’язок системи.
Розв’язання
1. Система (2.54) – це лінійна неоднорідна система двох диференціальних
рівнянь першого порядку з постійними коефіцієнтами. Крім того, ця динамічна
система автономна (час у явному вигляді в правій частині рівнянь системи
відсутній).
Tr A = 2, det A =
−
1 (див. зауваження 2.4).
2.1. Визначимо частинний розв’язок
)x,x(
*
2
*
1
(стаціонарну точку, точку
рівноваги) неоднорідної системи (2.54).
Прирівнявши похідні до нуля, одержимо систему:
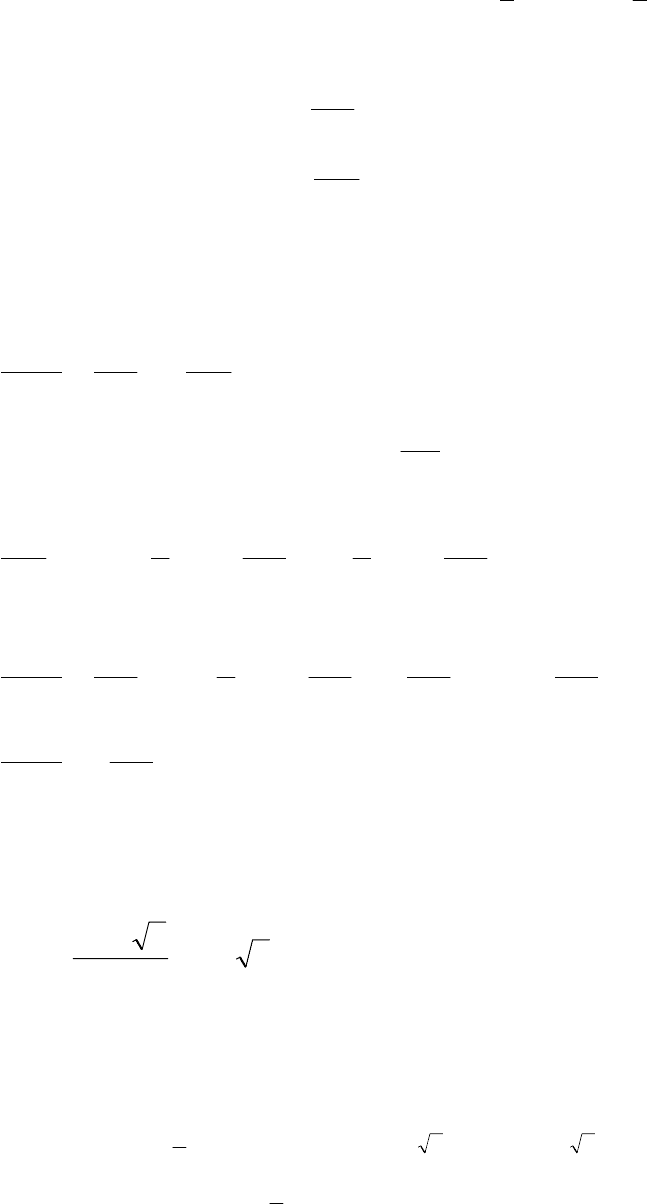
92
⎩
⎨
⎧
−+−=
−−=
,2xx0
,2x2x0
21
21
⇒
⎩
⎨
⎧
=−++−
+
=
,02x2x2
,2x2x
22
21
⇒
⎩
⎨
⎧
=
=
.0x
,2x
2
1
Отже, частинний розв’язок системи (2.50) має вигляд:
)x,x(
*
2
*
1
=(2, 0).
2.2. Визначимо загальний розв’язок
(
1
x
(t,C
1
,C
2
),
2
x
(t,C
1
,C
2
)) відповідної
однорідної системи диференціальних рівнянь:
⎪
⎩
⎪
⎨
⎧
+−=
−=
,xx
dt
dx
,x2x
dt
dx
21
2
21
1
(2.55)
Розглянемо два підходи.
2.2.1. Побудуємо відповідне диференціальне рівняння другого порядку.
З першого рівняння системи одержимо:
dt
dx
2
dt
dx
d
t
xd
21
2
1
2
−= .
Виразимо функцію
)(5,0
1
12
d
t
dx
xx −= з першого рівняння системи (2.55),
підставивши це рівняння в друге рівняння однорідної системи, і одержимо:
).
d
t
dx
x(
2
1
)
d
t
dx
x(
2
1
x
d
t
dx
1
1
1
11
2
−−=−+−=
Отже, диференціальне рівняння другого порядку має вигляд:
,
dt
dx
2x
dt
dx
))
dt
dx
x(
2
1
(2
dt
dx
d
t
xd
1
1
11
1
1
2
1
2
++=−−−=
.0x
dt
dx
3
d
t
xd
1
1
2
1
2
=+−
Характеристичне рівняння має вигляд:
012
2
=−−
λ
λ
.
21
2
222
2,1
±=
±
=
λ
.
Характеристичні числа
λ
1
,
λ
2
є дійсними числами і не дорівнюють одне
одному. Тоді загальний розв’язок однорідного диференціального рівняння, що
розглядається, має вигляд (формула 2.37):
t)21(
2
t)21(
1211
eCeC )C,C(t,x
−+
+= . (2.56)
Знайдемо функцію
).C,C(t,x
212
З першого рівняння системи (2.56)
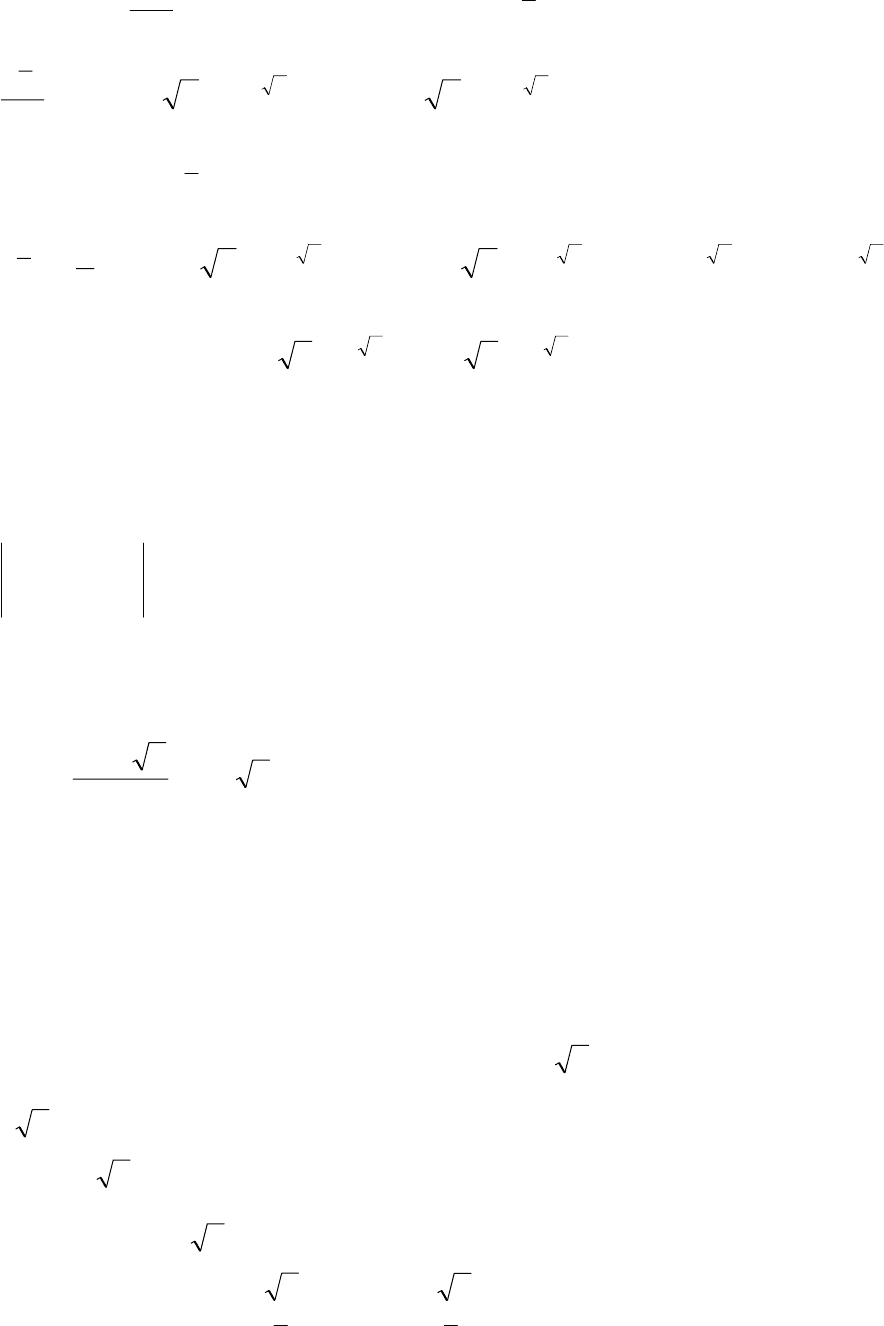
93
)
d
t
dx
x(5.0x
1
12
−= . Диференціюючи функцію )C,C(t,x
211
, одержимо:
t)21(
2
t)21(
1
1
e)21(Ce)21(C
dt
xd
−+
−++=
.
Отже, функція
)C,C(t,x
212
має вигляд:
)eCeCe)21(Ce)21(C(
2
1
x
t)21(
2
t)21(
1
t)21(
2
t)21(
12
−+−+
−−−++=
=
)e2Ce2C(5.0
t)21(
2
t)21(
1
−+
− . (2.57)
2.2.2. Визначимо розв’язок системи диференціальних рівнянь (2.57)
безпосередньо. Складемо характеристичне рівняння системи
|
А
−
λ
E|=0.
0
11
21
=
−−
−−
λ
λ
.
Отримуємо характеристичне рівняння (порівняйте з попереднім підходом!)
012
2
=−−
λ
λ
.
21
2
222
2,1
±=
±
=
λ
.
Для визначення власних векторів
Т1
2
1
1
1
)р,р(Р =
,
Т2
2
2
1
2
)р,р(Р =
побудуємо
систему лінійних однорідних алгебраїчних рівнянь:
⎪
⎩
⎪
⎨
⎧
==−+−
=−−
.2,1i,0р)1(р1
,0р2р)1(
i
2i
i
1
i
2
i
1i
λ
λ
(2.58)
Підставимо у систему (2.58) значення
21
1
+=
λ
, тобто
⎪
⎩
⎪
⎨
⎧
=+−
=−
.0р2р
,0р2р2
1
2
1
1
1
2
1
1
Отже,
Т1
)2,1(Р
µ
= , де
µ
− довільне дійсне число.
Для значення
21
2
−=
λ
Т2
)2,1(Р −=
ν
, де
ν
− довільне дійсне число.
Таким чином, функції
)C,C(t,x
211
, )C,C(t,x
212
мають вигляд (порівняйте з
(2.56), (2.57)):
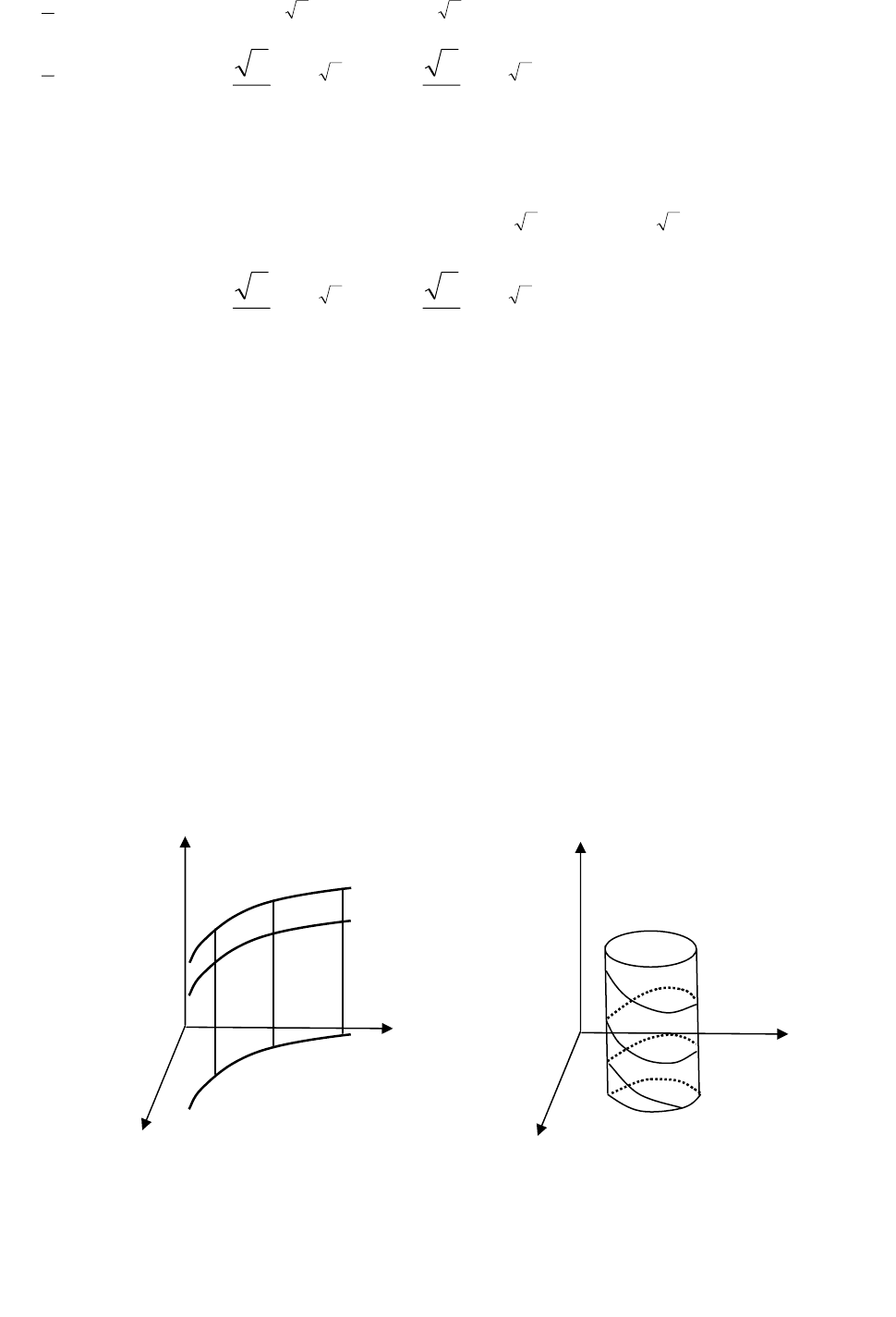
94
t)21(
2
t)21(
1211
eCeC )C,C(t,x
−+
+=
νµ
.
t)21(
2
t)21(
1212
e
2
2
Ce
2
2
C )C,C(t,x
−+
−= .
Отже, загальний розв’язок неоднорідної системи (2.51) лінійних
диференціальних рівнянь першого порядку має вигляд:
,2eCeC )C,C(t,х
t)21(
2
t)21(
1211
++=
−+
(2.59)
t)21(
2
t)21(
1212
e
2
2
Ce
2
2
C )C,C(t,x
−+
−= .
2.3.2. Фазова площина, фазовий портрет
Аналогічно п. 2.1.3 загальний розв’язок системи (2.45) – це сім’я
тривимірних інтегральних кривих у просторі
Ох
1
х
2
t (рис. 2.7).
Інше геометричне тлумачення можна одержати, якщо відносити систему
(2.45) не до осей
х
1
, х
2
, t тривимірного простору Ох
1
х
2
t, а до осей х
1
, х
2
площини
Ох
1
х
2
, вважаючи t параметром. У цьому випадку система (2.45) визначає криву,
рівняння якої можна одержати, виключивши з рівнянь системи параметр
t.
Площина
Ох
1
х
2
, яку ведено до розгляду, має назву фазова площина. Крива
на фазовій площині є
фазовою траєкторією, частина фазової площини, яка
заповнена фазовими траєкторіями називається
фазовим портретом системи
(2.45), функції х
1
(
t), х
2
(
t) – фазовими змінними.
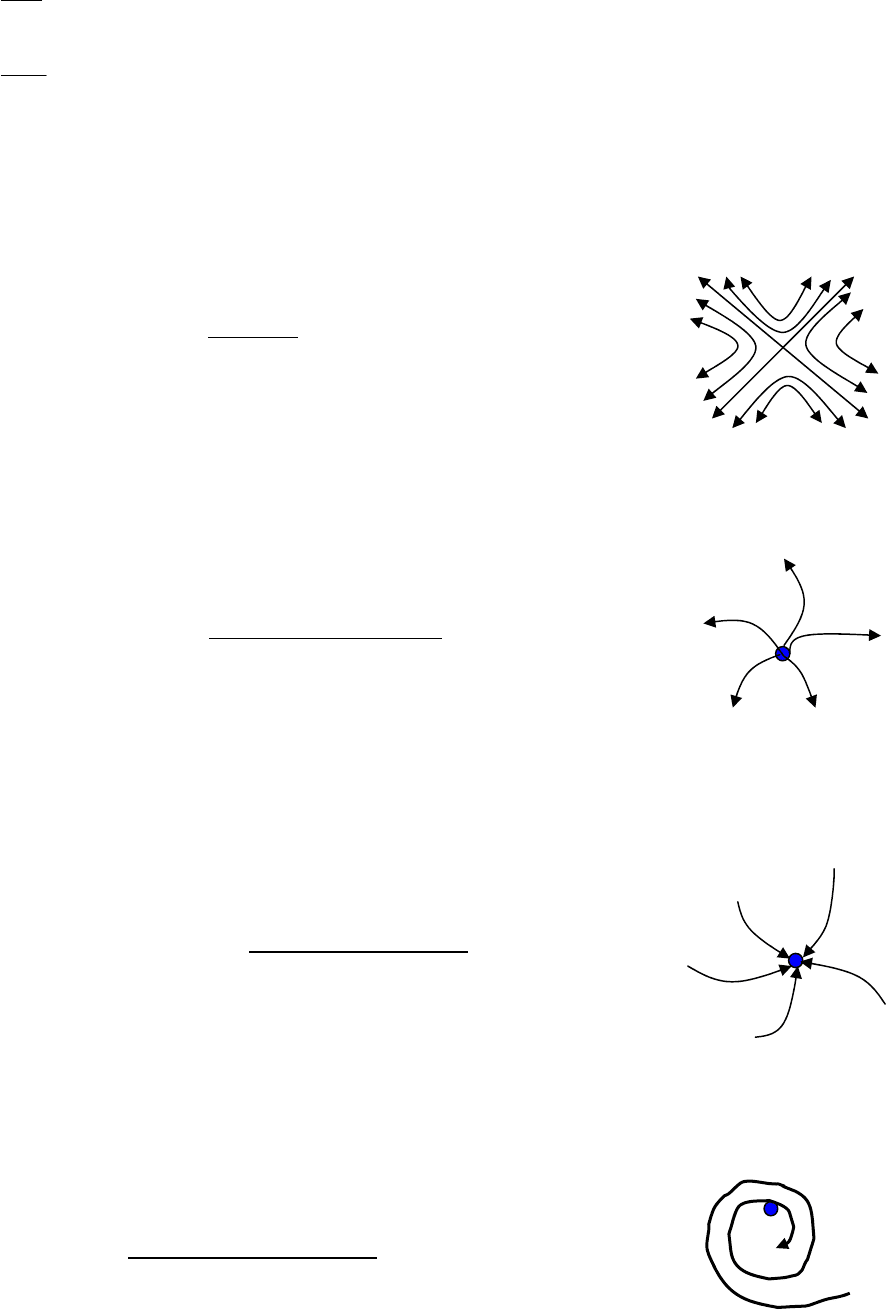
а) б)
Рис. 2.8. Поведінка розв’язків системи диференціальних рівнянь
у просторі Ох
1
х
2
t і на фазовій площині Ох
1
х
2
:
а) випадок монотонної поведінки системи;
б) випадок наявності періодичного розв’язку
x
1
x
2
t
x
1
x
2
t
O
O

95
Відзначимо, що така інтерпретація істотно відрізняється від геометричної
інтерпретації, описаної вище (див. визначення інтегральної кривої п. 2.1.3), її
можна назвати кінематичною, так як в цій інтерпретації відповідно до кожного
розв’язку ставиться рух точки вздовж кривої, а не крива в просторі.
Системи вигляду (2.42), (2.45) використовуються для опису еволюційних
процесів. Точка фазового простору визначає стан системи у визначений
момент часу. Прикладений до цієї точки вектор з координатами )
dt
dx
,
dt
dx
(
21
задає швидкість зміни стану. Точка, в якій цей вектор перетвориться на нуль
)0
dt
dx
dt
dx
(
21
== , називається положенням рівноваги, особливою точкою
(у нашому поданні ще й частковим розв’язком) системи (2.42).
Можна сказати, що перше рівняння в формулі (2.45) задає горизонтальну
складову швидкості руху точки у фазовій площині, а друге рівняння
−
вертикальну складову. Зрозуміло, що, якщо в деякій точці фазової площини
dx
1
/dt > 0, то функція x
1
(t) зростає, і розв’язок системи (2.45) рухається від цієї
точки вправо, а якщо
dx
1
/dt<0, то вліво. Аналогічно, якщо dх
2
/dt>0 (<0), то
точка рухається вгору (вниз).
Порівняємо геометричну інтерпретацію системи (2.45) у просторі Ох
1
х
2
t з
інтерпретацією на фазовій площині Ох
1
х
2
:
а) на кожну траєкторію фазової площини проектується сукупність
інтегральних кривих у просторі Ох
1
х
2
t. Ці криві виходять одна з одної заміною t
на t
−
C (рис. 2.8.а).
б) якщо точка (а, b) є станом рівноваги системи Р(а, b)=0; Q(a, b) = 0, то
інтегральна крива є прямою, яка рівнобіжна осі t. Ця пряма проектується на
площину (х, у) у єдину точку (а, b).
в) якщо система має періодичний розв’язок з періодом
α
, то в просторі
Ох
1
х
2
t відповідна інтегральна крива являє собою спіраль з кроком
α
. Ця
спіраль проектується на фазову площину в замкнуту криву (рис. 2.8.б).
При проекції спіралі тривимірної інтегральної кривої на площину
Ох
1
t або
Ох
2
t одержимо синусоїдальну криву, що показує динаміку змінної х
1
(t) або
х
2
(t).
2.3.3. Типи фазових портретів. Класифікація точок рівноваги
Розглянемо динамічну систему, що задається системою лінійних
диференціальних рівнянь (2.45)
96
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+=
+=
,xaxa
dt
dx
,xaxa
dt
dx
222121
2
212111
1
,
Нехай
1
λ
і
2
λ
– корені характеристичного рівняння виду (2.45) коефіцієнтів
системи.
1. Якщо
1
λ
і
2
λ
дійсні (
1
21
R, ∈
λλ
), то:
1.1. Якщо
1
λ
і
2
λ
різних знаків, то фазовий
портрет називається
сідлом (рис. 2.9). Дві пари
траєкторій проходять через стаціонарну точку, а
інші виглядають так, як горизонталі на карті
місцевості, котра є гірським перевалом. Саме
такий тип фазового портрету системи (2.56)
прикладу 2.5. Рис. 2.9. Сідло
1.2. Якщо
1
λ
> 0 і
2
λ
> 0 , то фазовий
портрет називається
нестійким вузлом . Кожна
фазова траєкторія примикає до особливої точки і
з часом розбігається (рис 2.10). Саме таким є
тип фазового портрету системи (2.54)
прикладу 2.6.
Рис.2.10. Нестійкий вузол
1.3. Якщо
1
λ
< 0 і
2
λ
< 0 , то фазовий
портрет називається
стійким вузлом. Усі
траєкторії проходять через стаціонарну точку і з
часом до неї збігаються (рис. 2.11).
Рис.2.11. Стійкий вузол
2. Якщо
1
λ
і
2
λ
комплексно-спряжені:
λ
1.2
=
α
± i
β
(див. зауваження 2.3), то
2.1. Якщо
α
< 0, то фазовий портрет
називається
стійким фокусом. Траєкторії
асимптотично наближаються до особливої точки,
навиваючись на неї у вигляді спіралей
(рис. 2.12).
Рис.2.12. Стійкий фокус

97
2.2. Якщо
α
> 0 (дійсна частина
додатна), то фазовий портрет називається
нестійким фокусом (рис. 2.13).
Рис.2.13. Нестійкий
фокус
2.3. Якщо
α
=0, тобто характеристичні
числа
λ
1.2
= ± i
β
мають тільки уявну частину, то
фазовий портрет називається
граничним циклом
(рис. 2.14).
Рис.2.14. Граничний цикл
Класифікація типів поведінки фазових кривих в околі особливої точки була
здійснена великим французьким математиком і філософом Анрі Пуанкаре
(1854—1912), який ввів також поняття
граничного циклу, що відіграє
найважливішу роль у різних додатках теорії диференціальних рівнянь.
Приклад 2.7. Побудувати фазовий портрет системи (2.54) (приклад 2.6.).
Розв’язання
Загальний розв’язок
(x(t), y(t)) неоднорідної системи (2.56) має вигляд (2.59):
,2eCeC )C,C(t,х
t)21(
2
t)21(
1211
++=
−+
t)21(
2
t)21(
1212
e
2
2
Ce
2
2
C )C,C(t,x
−+
−=
.
Розглянемо фазову площину
Оху. Координати точки рівноваги системи
(2.54) на фазовій площині (рис. 2.15) є
(2,0).
Динаміку системи визначає загальний розв’язок ))C,C(t,х, )C,C(t,х(
212211
однорідної системи (2.49):
)t()t(
) ,,(
eCeCCCtx
21
2
21
1211
−
+
+
=
,
t)21(
2
t)21(
1212
e
2
2
Ce
2
2
C )C,C(t,x
−+
−= .
Згідно з наведеною класифікацією – це
сідло.
Оберемо для побудови траєкторії чотири різних набори констант
(C
1
,C
2
),
наприклад,
(C
1
=2, С
2
=2), (C
1
=2, С
2
= – 2), (C
1
=–2, С
2
=2), (C
1
=–1, С
2
=–1).
Кожен з наборів C
1
,C
2
визначає фазову траєкторію. Для подання характеру
фазового портрету досить чотирьох наборів.
Для кожного з наборів констант
C
1
, C
2
будемо змінювати час t від 0 з кроком
0.05 і розраховувати значення
)t(x),t(x
21
для кожного набору констант. Дані
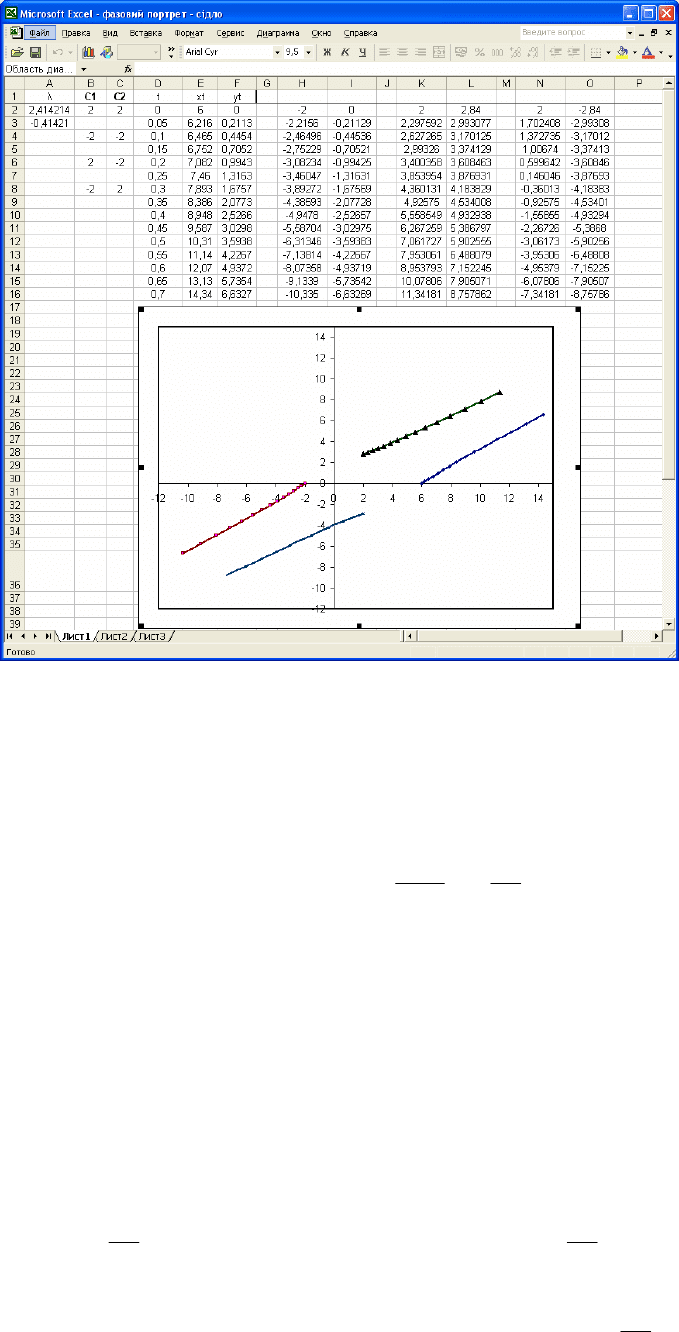
98
точки нанесемо на графік (рис. 2.15) з урахуванням положення точки рівноваги.
Рис. 2.15. Побудова фазового портрету системи (2.56) за допомогою
програмного середовища Еxcel
Приклад 2.8.
Побудувати фазовий портрет однорідного диференціального
рівняння другого порядку вигляду:
03y
dt
dy
4
d
t
yd
2
2
=++ .
Характеристичне рівняння має вигляд:
034
2
=
+
+
λ
λ
.
Корені даного характеристичного рівняння є такими:
}.3,1{
2,1
−−=
λ
Отже,
фазовий портрет є
стійким вузлом.
Загальний розв’язок диференціального рівняння має вигляд:
t3
2
t
121
eCeC )C,C(t,y
−
−
−= . (2.60)
Похідна
dt
dy
загального розв’язку є функцією
t3
2
t
1
eC3eC
dt
dy
−−
−−= .
У даному випадку фазовими змінними є функції
),
dt
dy
(у, тобто горизонтальна
99
координатна вісь фазової площини – це вісь значень функції y (2.60),
вертикальна вісь містить значення похідної
dt
dy
.
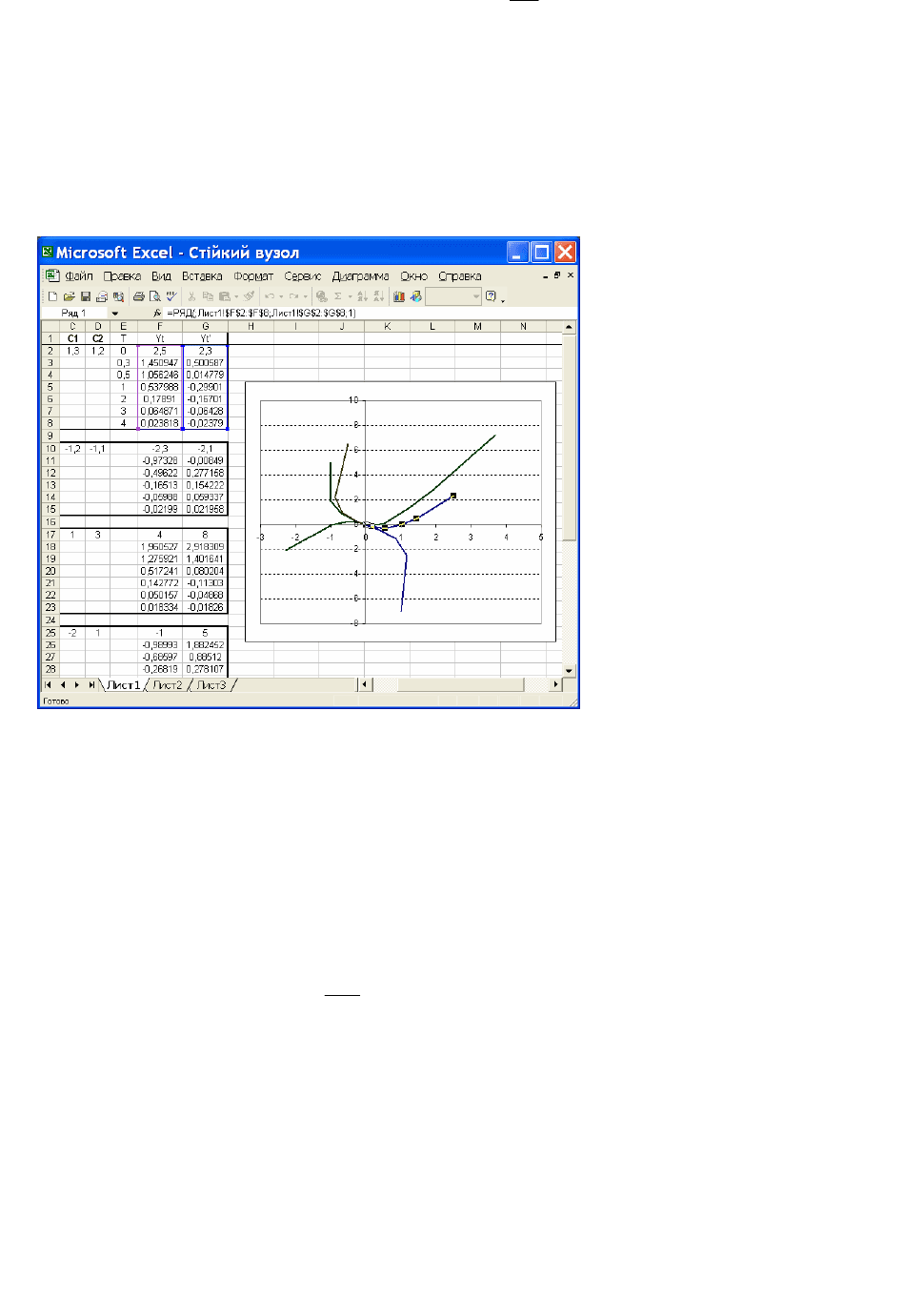
Для побудови фазового портрету фіксуємо значення постійних
С
1
і С
2
(для
першої фазової траєкторії
С
1
=1,3, С
2
=1,2 і змінюємо t в певному інтервалі (у
даному прикладі
]
4,0
[
t
∈ ). Цю операцію повторюємо для інших фіксованих
значень
С
1
і С
2
(рис. 2.16).
Рис. 2.16. Побудова в Excel фазового портрету ″стійкий вузол″
2.3.4. Аналіз стійкості розв’язків системи диференціальних рівнянь.
Атрактори динамічних систем
Розглянемо неавтономну систему диференціальних рівнянь:
)х,х,t(f
dt
dх
21i
i
= , i=1,2. (2.61)
Нехай x
i
=x
i
(t), i=1, 2, − розв’язок системи, який відповідає початковій умові
x
i
(t
0
)=x
i0
.
Визначення 1 (Стійкість за Ляпуновим). Розв’язок системи x
i
=x
i
(t), i=1,2 є
стійким за Ляпуновим, якщо для будь-якого дійсного числа
ε
> 0 існує дійсне
число
)
(
ε
δ
> 0, таке, що система нерівностей
δ
<− |yx|
ii 00
припускає
100
ε
<− )t(y)t(x
ii
для всіх t
≥
t
0
.
При цьому )t(у
i
− розв’язок, який визначається початковими умовами
.y)t(у
0i0i
=
Це означає, що незначна зміна початкових умов не спричинить значної
зміни розв’язку.
Визначення 2 (Нестійкість). Якщо для деякого дійсного числа
ε
> 0 такого
дійсного числа
)
(
ε
δ
не існує, то розв’язок x
i
=x
i
(t), i=1,2 є нестійким.
Визначення 3 (Асимптотична стійкість за Ляпуновим). Стійкий розв’язок
системи x
i
=x
i
(t), i=1,2 є асимтотично стійким, якщо можна вказати таке число r,
що з нерівності
r|yx|
0i0i
<−
випливає
0)t(y)t(xlim
ii
t
<
−
∞→
, i=1,2.
Асимптотично стабільна точка рівноваги називається
атрактором,
нестабільна точка рівноваги називається репелером.
Отже, стійкий вузол, стійкий фокус, граничний цикл є атракторами,
нестійкий вузол, нестійкий фокус, сідло
− репелерами.
2.3.5. Контрольні питання
1. Дайте характеристику лінійних диференціальних рівнянь другого
порядку.
2.
Чому дорівнює загальний розв’язок лінійного неоднорідного
диференціального рівняння другого порядку?
3.
Для чого застосовується характеристичне рівняння?
4.
Які випадки розв’язків характеристичного рівняння можуть мати місце?
5.
Дайте геометричну інтерпретацію комплексних чисел.
6.
Як знайти частковий розв’язок y* неоднорідного лінійного
диференціального рівняння з постійними коефіцієнтами?
7.
Скільки початкових умов має задача Коші для диференціальних рівнянь
другого порядку і які?
8.
Покажіть еквівалентність системи двох диференціальних рівнянь
першого порядку та диференціального рівняння другого порядку.
9.
Як визначається положення рівноваги системи диференціальних рівнянь.
10.
Дайте визначення фазової площини, фазової траєкторії та фазового
