Новожилова М.В., Коюда П.М. Моделювання економічної динаміки
Подождите немного. Документ загружается.


21
Розділ 2. Математичний апарат економічної динаміки
2.1. Диференціальні рівняння
2.1.1. Диференціальні рівняння першого порядку та їх застосування у
моделюванні економічних систем
Нагадаємо основні положення теорії диференціальних рівнянь, які
вивчались у курсі вищої математики [26,27,29] і стануть у пригоді надалі.
Загальний вигляд диференціального рівняння першого порядку є таким:
0)
dx
dy
y,F(x, = , (2.1)
де
x
– незалежна змінна, y – невідома функція,
dx
dy
–
похідна першого
порядку невідомої функції
y.
Якщо це рівняння можна розв'язати відносно y, тобто записати у вигляді:
y)f(t,
dx
dy
= , (2.2)
то говорять, що рівняння записане в нормальній формі (або у формі Коші).
Порядок диференціального рівняння визначається найвищим порядком
похідної невідомої функції, яка входить до рівняння.
Зауваження 2.1. У даному посібнику викладаються інструментальні засоби
дослідження поведінки економічних динамічних систем, тому далі, не
втрачаючи загальності, в якості незалежної змінної прийматимемо час
t, тобто
х=t і рівняння (2.2) набуде вигляду:
y)f(t,
dt
dy
= . (2.3)
Далі вважатимемо записи
d
t
dy
та у' еквівалентними.
Зауваження 2.2. В даному посібнику в якості математичної моделі
динамічних економічних систем розглядаються тільки звичайні диференціальні
рівняння, тобто шукана функція (або функції, якщо розглядається система
диференціальних рівнянь) залежить тільки від однієї незалежної змінної
t.
Загальним розв’язком диференціального рівняння першого порядку (2.1) в
області визначення
D функції f(t,y) є функція вигляду:
y =
ϕ
(t, C), (2.4)
де
C – довільна постійна.
Диференціальне рівняння має нескінченно багато розв’язків. Щоб з цієї

22
безлічі виділити якийсь конкретний розв’язок, потрібно визначити довільну
постійну
С, для чого необхідно вказати додаткову умову. Найчастіше така
умова задається у вигляді початкової умови
у (t
0
)= t
0
. (2.5)
Задача про знаходження розв’язків диференціального рівняння (2.1), що
задовольняють початковій умові (2.4), називається задачею Коші.
Як правило, задача Коші має єдиний розв’язок, який називається частинним
розв’язком рівняння (2.3). Умовою, що гарантує як існування розв’язку задачі
Коші для рівняння
у'=f(t,у), так і його єдиність у деякому околі початкової
точки
(t
0
, у
0
) є диференційованість функції f(t, у) у цьому околі. Однак можливі
випадки, коли задача має нескінченно багато розв’язків або взагалі не має
розв’язків.
Відзначимо, що в деяких випадках процес розв’язання диференціального
рівняння визначає розв’язок як неявну функцію, тобто як співвідношення
вигляду
Ф(t,y,С)=0, (2.6)
яке називається загальним інтегралом диференціального рівняння.
Відзначимо також, що процес розв’язання диференціального рівняння
прийнято називати інтегруванням цього рівняння.
Одним з найбільш простих, але досить важливих з погляду економічних
додатків типів диференціальних рівнянь першого порядку є рівняння зі
змінними, що діляться:
d
t
dy
=p(t)g(y), (2.7)
де
р(t) і g(y) − неперервні функції.
Для розв’язання цього рівняння необхідно поділити в ньому змінні, тобто
переписати рівняння в такий спосіб:
)( yg
dy
=p(t)dt (2.8)
у припущенні, що g(y)
≠
0. Тепер ліва частина рівняння містить тільки змінну y,
а права − тільки змінну t. Інтегруючи обидві частини рівняння (2.8), одержимо:
∫
)( yg
dy
=
∫
p(t)dt.
Останню рівність запишемо у видгляді наступного співвідношення:
G(y)=P(t)+C,
де
G(y) − будь-яка первісна для 1/g(y), а Р(t) − первісна для р(t). Таким
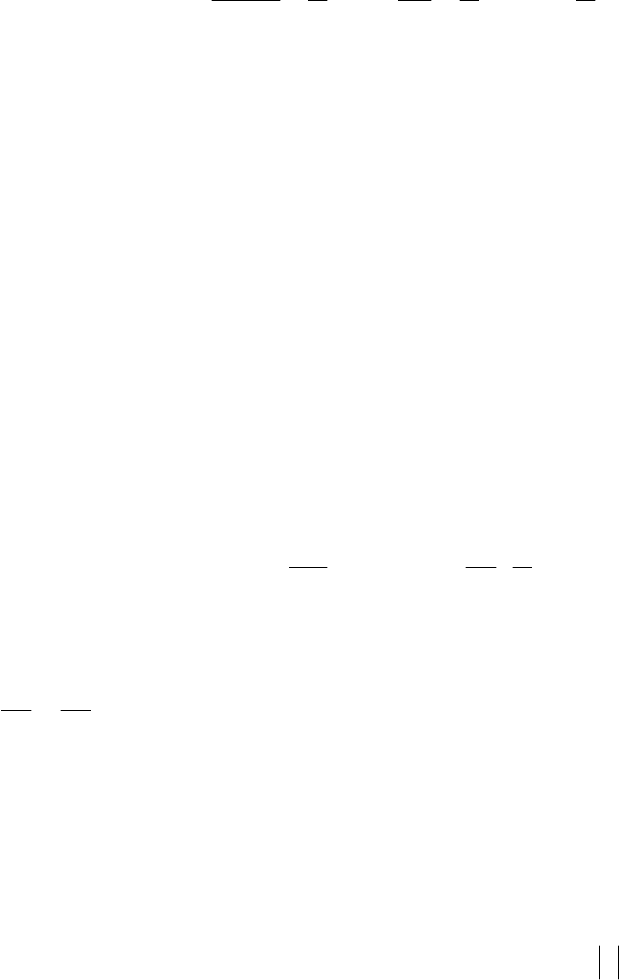
23
чином, знайдено загальний інтеграл рівняння (2.7).
Приклад 2.1. Нагадаємо, що еластичністю функції y=f(x) щодо змінної x
називають границю відношення відносного збільшення
y до відносного
збільшення змінної
x при ∆x
→
0
y
y
x
)x(f
y
x
x
y
y
x
y/x
x/y
limlim
x
x
′
=
′
=
∆
∆
=
∆
∆
→∆→∆ 00
. (2.9)
Цю границю позначають через
E
x
(y).
Величину
E
x
(y) при заданому значенні x називають також показником, або
коефіцієнтом еластичності. Еластичністю функції у відносно x є наближений
процентний приріст функції (підвищення або зниження), що відповідає
збільшенню незалежної змінної на 1%.
Еластичність функції застосовується під час аналізу попиту й споживання.
Наприклад, еластичність попиту
y щодо ціни х (або доходу х) – коефіцієнт, що
показує приблизно, на скільки відсотків зміниться попит (обсяг споживання)
при зміні ціни (або доходу) на 1%. Якщо |
E
x
(y) | > 1, то попит вважають
еластичним, якщо |
E
x
(y) | = 1 – нейтральним, якщо | E
x
(y) | < 1 – нееластичним
щодо ціни.
Отже,
задача є такою: знайти функцію, що має постійну еластичність k.
За умовою задачі маємо
,k
y
xy
=
′
тобто
k
y
x
dx
dy
=⋅
. (2.10)
Звідси, при природному припущенні, що
х ≠ 0, одержимо:
k
x
dx
y
dy
⋅=
.
Інтегруючи обидві частини отриманої рівності, знайдемо:
ln |
у| = k ln|x| + С.
Не втрачаючи загальності, подамо цю рівність у вигляді:
ln |
у| = k ln|x| + lnС або ln |у| = lnС
k
x.
Потенціюючи останнє співвідношення, одержимо вигляд функції, що має
постійну еластичність, яка дорівнює
k:
у=С х
k
.
Приклад 2.2. Швидкість знецінювання устаткування внаслідок його зносу
пропорційна в кожен даний момент часу його фактичній вартості. Початкова
вартість –
А
0
. Визначити, коли вартість устаткування знеціниться втричі.

24
Розв’язання.
Нехай А
t
− вартість устаткування в деякий момент часу t, t
шукане
– час, коли
вартість устаткування знеціниться втричі. Зміна вартості (знецінювання)
подається у вигляді різниці
(А
0
−
А
t
). Швидкість знецінювання
dt
d
(А
0
−
А
t
)
пропорційна фактичній вартості в даний момент
А
t
. Одержуємо задачу Коші
dt
d
(А
0
−
А
t
)=k А
t
,
(2.11)
А
t
|
t=0
= А
0
. (2.12)
Процес розв’язання рівняння (2.11) має вигляд:
−
dt
d
А
t
=k А
t
,
∫∫
−= kdt
A
dA
t
t
,
ln| А
t
|=
−
kt+ln|C|,
А
t
= C e
-kt
.
Для визначення довільної постійної
С використовуємо початкову умову
(2.12)
:
А
0
= C e
-k0
⇒ C =А
0
,
А
t
= А
0
e
-kt
. (2.13)
За умовою задачі
шукане
t
0
A
A
=3,
отже,
e
kt
=3 ⇒ t
шукане
= (ln3)/k.
Приклад 2.3. Нехай у(t )– кількість продукції, що випускається за час t; р –
ціна продукції. Сума інвестицій
І(t) пропорційна доходові ру(t)– з коефіцієнтом
пропорційності
m (m=const, 0<m<1). Збільшення швидкості випуску продукції
пропорційне збільшенню інвестицій з коефіцієнтом пропорційності
η
.
Знайти кількість продукції, що випускається галуззю за час
t, якщо в
початковий момент часу
t=t
0
, y=y
0
.
Розв’язання. За умовою задачі I(t)=m py(t), тому основним рівнянням є
диференціальне рівняння
)(tIy
d
t
d
η
=
або
.)(
η
tmpyy
d
t
d
=
Позначимо
k=mp
η
. Тоді попереднє рівняння набуде вигляду:

25
.kyy
d
t
d
=
(2.13)
Рівняння (2.13) – це диференціальне рівняння першого порядку зі змінними,
що діляться. Загальний розв’язок рівняння (2.13) має вигляд:
y=Ce
kt
.
Врахуємо, що
00
ytt
y
==
,
,
0
0
kt
Cey =
0
0
kt
eyC
−
= .
Звідси кількість продукції, що випускається галуззю за час t за даної
початкової умови
.
)
0
0
( ttk
eyy
−
=
Одним із важливих окремих випадків диференціальних рівнянь зі змінними,
що діляться, є так звані
автономні рівняння. Це рівняння вигляду:
d
t
dy
=g(y). (2.14)
Такі рівняння часто зустрічаються в різних питаннях економічної динаміки.
Відсутність часу (незалежної змінної) у правій частині рівняння (2.14) можна
трактувати як незмінність законів, за якими розвивається економічна система в
розглянутий проміжок часу.
Якщо y* − корінь рівняння g(y) = 0 (тобто похідна
dt
dy
шуканої функції
дорівнює нулю), то у=y*(=const) є розв’язком рівняння (2.14). Такий розв’язок
називається
стаціонарним (стаціонарна точка).
Економіко-математичні моделі, що базуються на диференціальних
рівняннях, називаються
моделями зростання з неперервним часом.
Відзначимо, що існують також дискретні аналоги цих моделей, що будуть
розглянуті нижче.
2.1.2. Геометричний зміст розв’язків диференціального рівняння
Загальний розв’язок (2.4) y =
ϕ
(t,C) рівняння (2.3) визначає на площині y0t
сім’ю кривих, що залежить від параметра С. Ці криві називаються
інтегральними.
Приклад 2.4. Розглянемо геометричну інтерпретацію загального розв’язку
у=С х
k
задачі прикладу 2.1. Ряд 1 на рис.2.1. відповідає значенню довільної
26
постійної С=1, ряд 2 – значенню С=2, ряд 3 – значенню С=3.
Візьмемо деяку точку (t
0
, y
0
) з області визначення D функції f(t,y). Нехай
у =
ϕ
(t) − інтегральна крива, що проходить через цю точку (тобто y
0
=
ϕ
(х
0
)). З
рівняння (2.3) випливає, що
dt
d
ϕ
(t
0
)= f (t
0
, y
0
).
Таким чином, кутовий коефіцієнт дотичної до інтегральної кривої у точці
(t
0
, y
0
), дорівнює (при t = t
0
) числу f(t
0
, y
0
).
Точки, через які не проходить жодна інтегральна крива або проходить
більше ніж одна інтегральна крива, називаються
особливими точками даного
диференціального рівняння.
Із співвідношення (2.4) за допомогою вибору константи С можна одержати
рівняння будь-якої інтегральної кривої, тобто можна одержати будь-який
частковий розв’язок. Таким чином, сім’я інтегральних кривих рівняння (2.10)
на рис. 2.1. складається з трьох часткових розв’язків.
0
50
100
150
200
250
300
350
400
1234567891011
Ряд1
Ряд2
Ряд3
Рис. 2.1. Сім’я інтегральних кривих рівняння (2.10) – функції з
еластичністю E
x
(y)= 2
2.1.3. Лінійні диференціальні рівняння першого порядку
Диференціальне рівняння називається лінійним, якщо воно є рівнянням
першого ступеню щодо шуканої функції y і її похідної
dt
dy
. Загальний вигляд
лінійного рівняння першого порядку такий:
dt
dy
+
P(t)y=Q(t). (2.15)

27
Якщо права частина рівняння має вигляд Q(t) = 0, то рівняння (2.15)
називається лінійним однорідним, у противному випадку воно називається
неоднорідним.
Будемо далі розглядати окремий випадок рівняння (2.15) –рівняння з
постійними коефіцієнтами вигляду:
dt
dy
+ аy=В, (2.16)
де а, В – деякі постійні.
Однорідне диференціальне рівняння, яке відповідає рівнянню (2.16), має
вигляд:
dt
dy
+ аy=0.
(2.17)
Теорема 1. Загальний розв’язок лінійного неоднорідного диференціального
рівняння (2.16) y(t) − це сума часткового розв’язку y* цього рівняння і
загального розв’язку
y(t,C) відповідного йому лінійного однорідного
диференційного рівняння (2.17):
y(t)= y* + y(t,C).
Відмітимо, що теорема 1 є вірною незалежно від порядку лінійного
неоднорідного диференціального рівняння.
Розв’язок однорідного лінійного рівняння (2.17) не вимагає спеціального
розгляду, оскільки рівняння (2.17) одночасно є рівнянням зі змінними, що
розділяються (див. п. 2.1.1.).
Отже, загальний розв’язок однорідного рівняння (2.17) має вигляд:
y (t, C)=C
at
e
−
. (2.18)
Частковий розв’язок y* рівняння (2.17) визначається за допомогою варіації
довільної постійної. Будемо шукати розв’язок y* рівняння (2.16) у вигляді
y*=K,
(2.19)
де K − деяка невідома постійна.
Підставимо значення (2.19) у рівняння (2.16), враховуючи, що
dt
*dy
=0
. Тоді
аK =В, таким чином y* = K =
a
B
.
Отже, загальний розв'язок лінійного неоднорідного диференційного
рівняння (2.16) у(t) = y* +
y
(t, C) буде таким:

28
у(t)=
a
B
+ C
at
e
−
. (2.20)
2.1.4. Найпростіша модель рівноваги
Рівновага
− це такий стан об'єкта, в якому об’єкт знаходиться за відсутності
зовнішніх впливів. Задачі економічної динаміки включають як опис процесів
виходу до стану рівноваги, так і визначення процесів трансформації самого
цього стану під впливом зовнішніх сил.
Розглянемо просту економічну систему в стані рівноваги та опишемо
динаміку такої системи
за допомогою диференційного рівняння.
Диференціальне рівняння пов'язує зміну показника (нехай наша система
описується одним показником
y(t), або просто y) зі швидкістю його руху
dt
dy
.
Нехай швидкість зміни показника
y пропорційна величині його відхилення
від рівноважного значення
y
e
. Отже, чим далі показник відхилився від
рівноважного значення, тим швидше він прагне повернутися до положення
рівноваги. Якщо в рівнянні присутня тільки перша похідна
y за часом, а сам
зв'язок лінійний, то воно є лінійним неоднорідним диференціальним рівняння
першого порядку з постійними коефіцієнтами. Нехай воно має такий вигляд:
у' = k(y - y
e
), (2.21)
де
k − коефіцієнт пропорційності.
У цьому рівнянні
ky
e
− вільний член; без нього рівняння y=ky є однорідним і
його загальним розв’язком є сім’я функцій
y = Сe
kt
. Вихідне неоднорідне
рівняння (2.21) має
частковий розв’язок y = y
e
(характеризує величину y у
стані рівноваги), а
загальний його розв’язок є сума часткового розв’язку
неоднорідного рівняння (2.21) і загального розв’язка відповідного однорідного
рівняння, тобто рівняння вигляду:
y = y
e
+Се
kt
. (2.22)
Довільну постійну С можна визначити, застосовуючи початкову умову
вигляду
y
|t=0
= y(0). Отже, з початкової умови одержимо:
С=y(0) − y
e
, і y(t) = y
e
+(y(0) - y
e
)e
kt
.
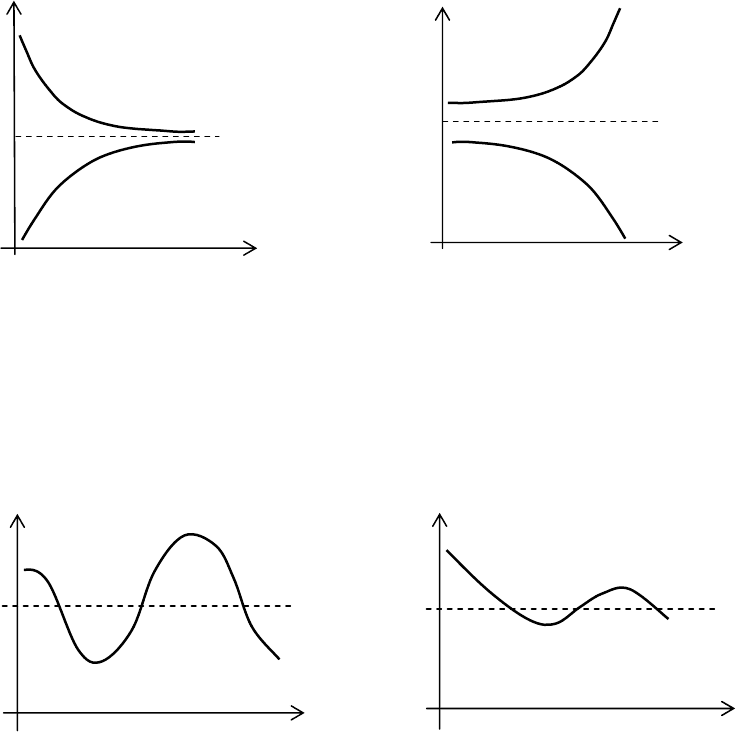
Якщо k < 0, то е
kt
→ 0 при k→
∝
. Рівновага стійка, тобто при відхиленні
величини
y(t) від значення y
e
, процес у часі знову збігається до значення
рівноваги (рис 2.2).
При
k > 0 величина e
kt
→
∝
і відповідно ряд значень y(t) розбігається (якщо
початковий стан не збігається зі станом рівноваги). Поведінку системи при
k > 0 проілюстровано на рис. 2.3.
29
Рис.2.2. Збіжність Рис.2.3. Монотонна розбіжність
до рівноважного стану процесу
Поведінка динамічних систем може також описуватися, наприклад,
графіками рис. 2.4 − 2.5.
Рис.2.4. Коливальна розбіжність Рис.2.5. Коливальна збіжність
2.1.5. Контрольні питання
1. Запишіть диференціальне рівняння в нормальній формі (формі Коші).
2.
Дайте характеристику диференціальних рівнянь зі змінними, що
розділяються.
3.
Що таке еластичність функції?
4.
Що таке автономні рівняння?
5.
Подайте геометричний зміст розв’язків диференціального рівняння.
6.
Дайте характеристику лінійних диференціальних рівнянь першого
порядку.
7.
Як знайти частковий розв’язок лінійного неоднорідного
диференціального рівняння?
8.
Як знайти загальний розв’язок лінійного однорідного диференціального
рівняння?
9.
Як знайти загальний розв’язок лінійного неоднорідного
t
у
1
(
0
)
y
e
y
t
y
y
2
(0)
y
e
y
2
(0)
t
y
y
2
(0)
y
e
y
2
(0)
t
y
у
1
(
0
)
y
e
30
диференціального рівняння?
10.
Дайте геометричну та математичну інтерпретацію точки рівноваги.
2.1.6. Завдання для самостійної роботи
1.Використовуючи програмне середовище Excel (або інше програмне
середовище), побудувати програму розв’язання лінійного диференціального
рівняння першого порядку
)y,х(f
dx
dy
= , де xey)х(f
x
−+= 2, з початковою
умовою
25,0
)
0
(
y = на інтервалі [0, 1] методами Ейлера та Рунге-Кутта [30],
ітераційні формули яких подано нижче. Крок
h=0,01.
Метод Ейлера
khxx
),y,x(fhyy
k
kkkk
⋅+=
⋅+=
+
0
1
Метод Рунге-Кутта
).,(
),
2
,
2
(
),
2
,
2
(
),,(
,
6
)22(
34
23
12
1
43211
hmyhxfm
h
my
h
xfm
h
my
h
xfm
yxfm
h
mmmmyy
kk
kk
kk
kk
kk
++=
++=
++=
=
⋅++++=
+
Результат подати у вигляді таблиці, в якій містяться значення функції, отримані методом Ейлера та
методом Рунге-Кутта. Порівняти отримані результати графічно.
На рис. 2.6. наведено приклад виконання даного завдання студентом третього курсу факультету
Економіки та менеджменту Харківського державного технічного університету будівництва та архітектури
(ХДТУБА) І. Кононенко. Програму написано у програмному середовищі
Delphi (рис.2.6).
