North, Gerald R., Erukhimova Tatiana L. Atmospheric Thermodynamics: Elementary Physics and Chemistry

Подождите немного. Документ загружается.

8.5 Equilibrium constant 207

As the reaction proceeds the products of this reaction (C and D) become sufﬁciently

dense in number that they will begin to react and form A and B through the reverse

reaction:

C + D → A + B. (8.51)

When eventually the rate of the forward reaction (8.50) is the same as the rate of

the reverse reaction (8.51), the system is in chemical equilibrium. We can combine

(8.50) and (8.51) and write

A + B

 C + D. (8.52)

If we were trying to ﬁnd the rate for which the reaction (8.52) proceeds from the

point of view of the individual gas molecules, we would say the rate of increase of

the concentration of C is given by

[C] = k

[A][B] − k

[C][D]

[D]

=−

[A]

=−

[B] (8.53)

where k

and k

are the reaction rate coefﬁcients for forward and reverse reactions

respectively. The equation simply states that the rate of buildup of C is the sum of

the rates of reactive collisions of A and B minus the reverse process in which

C and D react. The ﬁrst term must be proportional to the respective number

densities and similarly for the second (loss) term. Since for every creation of a

C molecule there must be a B molecule, these rates of formation must be equal

to each other and equal to the negative of the rates of formation of the A and B

molecules.

In equilibrium the rates of change of the species are zero. This means

[C] = 0 equilibrium (8.54)

K =

[C][D]

[A][B]

. (8.55)

The constant K is called the equilibrium constant for the reaction. If K is known,

we can determine the ratios of concentrations of the product and reactant gases in

equilibrium.

208 Thermochemistry

For the case of a general reaction

a A + b B → c C + d D, (8.56)

the equilibrium constant is (as derived in physical chemistry texts):

K =

[C]

[D]

[A]

[B]

(8.57)

The rule can be generalized to cases where more than two species are on each side

of the equation.

It is seen from (8.57) that when the inverse reaction rate is very small, which

means that products dominate over reactants, K is large. Small K means there will

be a relatively large concentration of the reactant species.

The equilibrium constant depends on collision dynamics and in principle

should have a strong temperature dependence, since the intermolecular relative

velocity will be an important factor in the rearrangements. To ﬁnd the temperature

dependence of the equilibrium constant, let us write the reaction rate coefﬁcients

for the forward and reverse reactions (8.52). Using the Arrhenius equation (8.59)

the reaction rate coefﬁcient for the forward reaction, k

,is

(T ) = A

exp



−E

act

∗



. (8.58)

The reaction rate coefﬁcient for the reverse reaction, k

,is

(T ) = A

exp



−E

act

+ H

◦

∗



. (8.59)

The equilibrium constant

K(T ) =

∝ exp



−

◦

∗



(8.60)

Hence, knowing the standard enthalpy associated with a reaction provides

information about the equilibrium concentrations of the species.

Example 8.9 Consider the recombination of OH and O:

OH + O → O

+ H. (8.61)

Write the expression for the equilibrium constant. By using formula (8.60) ﬁnd out

whether the products will dominate over reactants at high or low temperatures.

8.5 Equilibrium constant 209

Answer: In order for the reaction to proceed, an OH molecule has to bump into an

O atom in the same tiny volume. The rate of growth term must be proportional to

[OH][O]. The equilibrium constant is

K =

][H]

[OH][O]

. (8.62)

To ﬁnd the temperature at which the forward reaction will be favored we need to

ﬁnd the standard enthalpy:



◦

= H

◦

) + H

◦

(H) − H

◦

(OH) − H

◦

(O)

= (0 + 217.97 − 38.96 − 249.17) kJ mol

−1

=−70.2 kJ mol

−1

. (8.63)

Since 

◦

is negative, from (8.60) we have that the equilibrium constant K is

larger with lower temperature. This explains why the products of reaction (8.61)

will dominate over reactants at the lower temperatures.



The next step is to ﬁnd the connection between the equilibrium constant and

the Gibbs energy. The equilibrium of the chemical reaction implies that at a given

temperature there exist partial pressures of the gases involved in the reaction with

which the rate of the forward reaction is equal to the rate of the reverse reaction. Let

us express the equilibrium constant in terms of partial pressures of each constituent.

Using the Ideal Gas Law for the molar concentrations we obtain:

K =

∗

T )

∗

T )

∗

T )

∗

T )

∗

T )



, (8.64)

where the p

are partial pressures and  = (a +b) −(c +d ). We can rewrite (8.64)

in the form:

K = K

∗

T )



, (8.65)

where

[equilibrium constant for ideal gases]. (8.66)

is used as an equilibrium constant for chemical reactions involving species in

the gaseous state.

For a reversible transformation at constant temperature the change of Gibbs

energy is (see (4.97))

dG = V dp. (8.67)

210 Thermochemistry

For 1 mol of ideal gas

G =

∗

dp. (8.68)

(Note that the molar Gibbs energy

G is also called the chemical potential.) By

integrating this equation from the standard pressure level of 1 atm to some arbitrary

pressure level p holding T constant we obtain

G − G

◦

= R

∗

T ln p, (8.69)

where p is in atm. In this formula

G is the Gibbs energy at pressure p and temperature

T and

◦

is the Gibbs energy at 1 atm and temperature T .

Using (8.69) we can write the change of Gibbs energy for the general chemical

reaction



G =[cG(C) + dG(D)]−[aG(A) + bG(B)] (8.70)

in the form



G =[c

◦

(D) − aG

◦

(A) − bG

◦

(B)]

+ cR

∗

T ln p

+ dR

∗

T ln p

− aR

∗

T ln p

− bR

∗

T ln p

= G

◦

+ R

∗

T ln

)

. (8.71)

The argument of the logarithmic function in the last formula is the equilibrium

constant K

(see (8.66)). Therefore,



G = G

◦

+ R

∗

T ln K

. (8.72)

At equilibrium 

G = 0, and the change of Gibbs energy at a pressure of 1 atm and

arbitrary temperature T , 

◦

, is related to the equilibrium constant at pressure p

and temperature T , K

, by the simple relation:



◦

=−R

∗

T ln K

. (8.73)

The equation (8.73) tells us that if 

◦

is positive, K

should be less than unity,

which means that at equilibrium the concentrations of the reactants will exceed

those of the products. If, on the other hand, 

◦

is negative and, moreover, is

large, then K

is large and the products will dominatein the equilibrium.

8.6 Solutions 211

For standard conditions at a pressure of 1 atm and a temperature of 25

◦

Cwe

obtain, in joules,

G

◦

=−R

∗

× T

× ln K

=−2478.9 × ln K

(8.74)

The change in Gibbs energy G is especially useful because it simultaneously

takes into account both the First and Second Laws of Thermodynamics. It does so

in such a way that if the temperature and pressure are held constant (and they often

are in atmospheric problems) we have a function which can be applied much more

broadly.

Example 8.10 Consider the reaction of recombination of NO

and O

+ O

 NO

+ O

. (8.75)

Do the reactants or products dominate for the forward reaction at 1 atm and 25

◦

Answer: We have to ﬁnd the change of the Gibbs energy for this reaction.



◦

= (115.9 + 0 − 51.3 − 163.2) kJ mol

−1

=−98.6 kJ mol

−1

. (8.76)

From (8.74) we obtain K

= 1.9 ×10

. With such a large value of K

the products

will dominate for the forward reaction at equilibrium.



8.6 Solutions

Chemistry refresher A solution is a homogeneous mixture of several components.

Consider a two-component solution. One component has a mole fraction η

(the ratio

of the number of moles of a component to the total number of moles), and the other

component has mole fraction η. The component with a greater mole fraction, let it be

, is called the solvent. The solvent determines the state of matter of the solution

(gas, liquid or solid). The component with the smaller mole fraction, η, is called the

solute. In Chapter 5 we considered a cloud droplet as an example of a solution with

water as a solvent and the salt as a solute. A solution of a salt in a solvent such as

water is saturated when the rates of dissolving and crystallization are equal. In this

case there could be some substance in the crystalline form present in the composite

system. For example, there might be a salt crystal inside a cloud droplet. The amount

of dissolved material (solute) in the saturated solution is called its solubility, which

might depend strongly on temperature and weakly on pressure. We are interested in

the effect of the dissolved solute on the vapor pressure of the solvent.

Raoult’s Law Consider a solution that is in chemical equilibrium. The vapor

pressure of each component of the solution is approximately

212 Thermochemistry

= p

pure

(8.77)

where p

pure

is the vapor pressure of a pure ith component and η

is the mole fraction of

an ith component of the solution. The solution is called ideal when both solvent and

solute obey Raoult’s Law. Raoult’s Law applies when the components of the solution

are present in high concentrations. We used Raoult’s Law when we considered the

equilibrium vapor pressure over a droplet containing dissolved electrolytes.

For solutions at low concentrations the vapor pressure of the solute obeys Henry’s

Law. According to Henry’s Law, the vapor pressure of a solute, p, is a product of the

mole fraction of the solute, η, and an empirical tabulated constant, K

, expressed in

units of pressure:

p = K

η. (8.78)

Generally, the value of K

increases with increasing temperature. Thus, at the same

pressure the mole fraction of a solute decreases with increasing temperature.

When the atmospheric pressure decreases, the partial pressure of a gas decreases,

and the molar solubility of a gas decreases. For example, high in the mountains the

atmospheric pressure is low; as a result the solubility of oxygen in human blood

decreases, which can cause respiration problems. At the opposite end, the higher the

pressure, the higher the solubility of gases. You might say the gas is “squeezed” into

the solution.

Example 8.11 Calculate the molar solubility of nitrogen dissolved in1lofwater

at 25

◦

C and atmospheric pressure of 1 atm. Henry’s Law constant for nitrogen at

◦

C is 8.68 × 10

Pa. The percentage by volume of N

in dry air is 78.1.

Answer: The partial pressure of N

at 1 atm is p

= 0.781 × 1 atm = 7.91 ×

Pa. From Henry’s Law η

= p

= (7.91 × 10

Pa)/(8.68 × 10

Pa) =

9.1 × 10

−6

. The mole fraction of nitrogen η

= ν

/(ν

+ ν

) ≈ ν

/ν

since ν

 ν

. The number of moles of H

Oin1lis(1000/18) mol. Then,

= (9.1 × 10

−6

× 1000/18) mol = 5.05 × 10

−4

mol. The molar solubility of

nitrogen is 5.05 × 10

−4

mol l

−1

. 

Example 8.12 Calculate the molar solubility of CO

in moles per liter dissolved

in water at 25

◦

C and CO

pressure of 2.4 atm (pressure used to carbonate soda).

Henry’s Law constant for CO

at 25

◦

C is 1.67 × 10

Pa.

Answer: 2.4 atm = 2.43 × 10

Pa. The mole fraction of CO

according to Henry’s

Law is η

= p

= (2.43 × 10

Pa)/(1.67 × 10

Pa). Since there is

(1000/18) mol of H

O in 1 l, the molar solubility of CO

is (2.43 × 10

Pa ×

1000/18 mol l

−1

)/(1.67 ×10

Pa) = 8.1 ×10

−2

mol l

−1

. When one opens a bottle

of soda, the pressure decreases; as a result the solubility of CO

decreases, and the

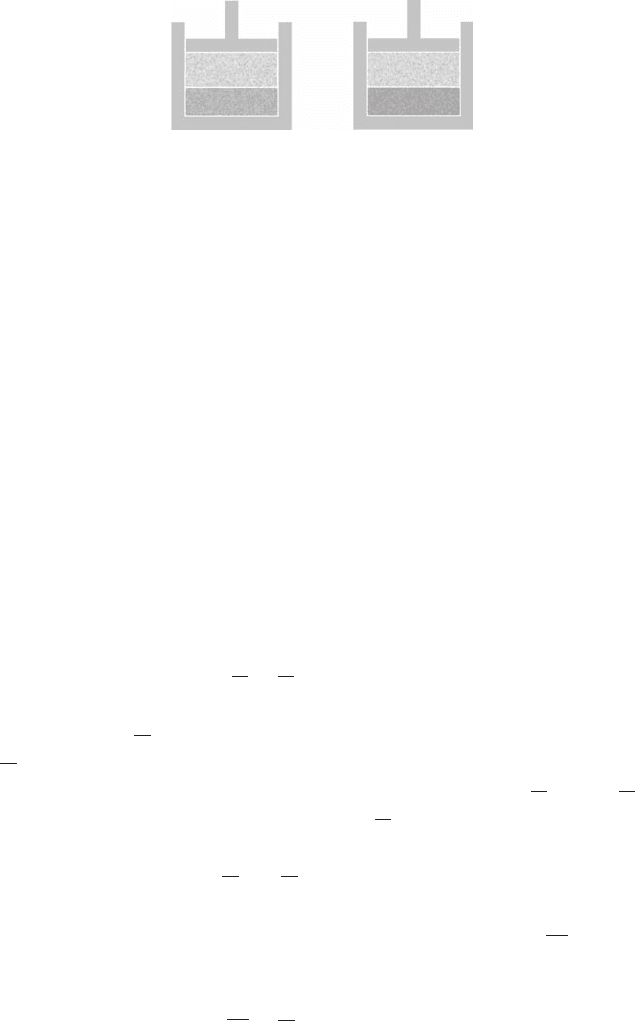
8.6 Solutions 213

(a)

(b)

pure solvent solution

vaporvapor

Figure 8.7 Notation. (a) Pure solvent in equilibrium with its vapor at pressure e

(b) Solution in equilibrium with the solvent’s vapor at pressure e



bubbles of CO

emerge from the solution. At higher temperature the solubility of

decreases since Henry’s constant increases (soda from a fridge sparkles less

than soda held at room temperature).



8.6.1 Molar Gibbs energy of an ideal solution

In this section we will ﬁnd out how the Gibbs energy of a pure solvent changes when

a small amount of solute is added. We will consider liquids that are at equilibrium

with their vapors. This means that the Gibbs energy of the vapor is equal to the

Gibbs energy of the liquid. Let us denote the equilibrium vapor pressure over a

pure solvent as e

, and the equilibrium vapor pressure over the solution as e



(see

Figure 8.7). From (8.69) the molar Gibbs energy (the Gibbs energy per mole) of

vapor at pressure e

G = G

◦

+ R

∗

T ln e

(8.79)

where e

is in atm, G is the molar Gibbs energy

at pressure p and temperature T

and

◦

is the molar Gibbs energy at 1 atm and temperature T . Since at equilibrium

the molar Gibbs energy of a liquid is equal to that of the vapor,

vapor

= G

liquid

the Gibbs energy of a pure solvent, denoted as

,is

= G

◦

+ R

∗

T ln e

. (8.80)

When a solute is added, the molar Gibbs energy of the solvent,



, which is at

equilibrium with its vapor at pressure e



,is



= G

◦

+ R

∗

T ln e



. (8.81)

The molar Gibbs energy is often called the chemical potential.

214 Thermochemistry

Subtracting (8.80) from (8.81), we obtain the difference between the molar Gibbs

energy of the solvent in the solution and the pure solvent:



− G

= R

∗

T ln



. (8.82)

From Raoult’s Law, e



= η

, where η

is the mole fraction of solvent (e.g.

water) in the solution. Then,



− G

= R

∗

T ln η

. (8.83)

We will consider a dilute solution, when the mole fraction of the solute, η , is much

smaller than that of the solvent, η  η

. Since η + η

= 1, we rewrite (8.83)as



− G

= R

∗

T ln (1 − η). (8.84)

Taking into account that for η  1, the logarithmic function can be written as

ln(1 −η) ≈−η, we obtain

− G



= R

∗

T η. (8.85)

We will use (8.85) in the next section to ﬁnd the temperature at which the solution

boils and freezes.

8.6.2 The elevation of the boiling point and the lowering of the freezing point

of a solution

When some solute is dissolved in a pure solvent, the boiling and freezing points of

the solution are not the same as for the pure solvent. We will show that the change

is proportional to the amount of solute. We will consider nonvolatile solutes (for

example, a salt). In this case the vapor of the solute is a pure gas.

Example 8.13 Show that the addition of a dissolved solute in a solution will elevate

the boiling point compared to the boiling point of pure solvent.

Answer: The boiling point is the temperature at which the saturated vapor pressure

of a liquid is the same as the atmospheric pressure. We consider two cases.

Case 1: equilibrium between a pure solvent and its vapor (see Figure 8.8a). The

pure solvent boils at temperature T

. The vapor pressure is 1 atm. At equilibrium,

the molar Gibbs energies of the pure solvent, denoted below as

, and its vapor,

denoted as

, are equal to each other:

, p) = G

, p). (8.86)

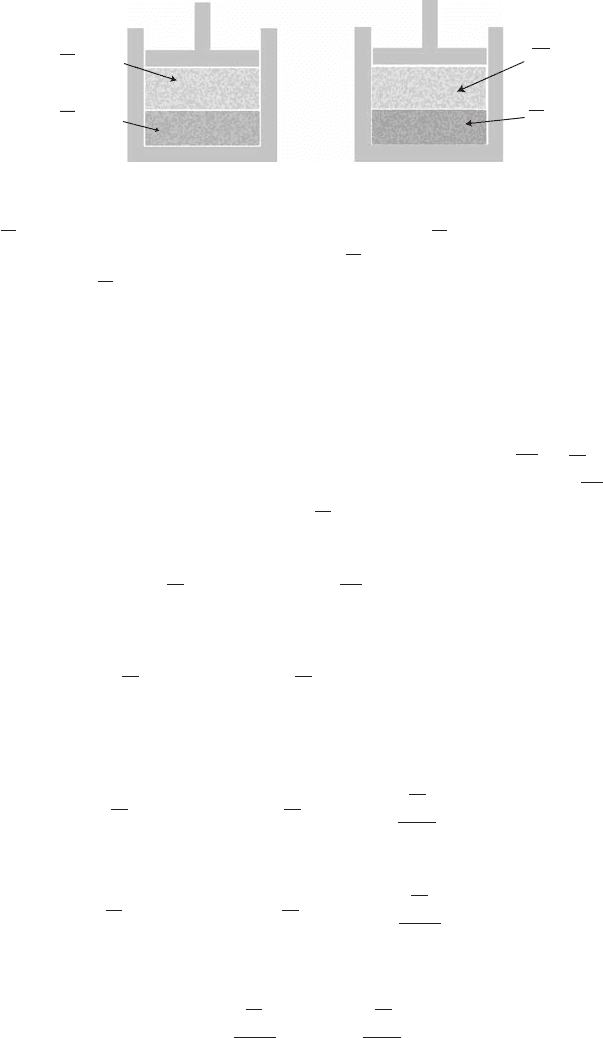
8.6 Solutions 215

pure solvent

vapor

(a)

(b)

(T, p)

G⬘(T, p)

solution

, p)

Figure 8.8 Notation. (a) Molar Gibbs energy for the vapor over the pure solvent,

, p), and molar Gibbs energy for the pure solvent, G

, p). (b) Molar Gibbs

energy of solvent vapor over the solution,

(T , p), and molar Gibbs energy of

the solvent,



(T , p).

Case 2: there is an amount η of nonvolatile solute in the solvent. The solution is

at equilibrium with the solvent’s vapor (see Figure 8.8b). The vapor pressure at the

boiling point is 1 atm, the same as in case 1, but the boiling point differs. Assume

that the solution boils at a temperature T = T

+ T where T  T

. From

(8.85) the molar Gibbs energy of the solvent in the solution is



= G

− R

∗

T η.

At equilibrium, the molar Gibbs energy of the solvent in the solution,



, is equal

to the molar Gibbs energy of the vapor,

+ T , p) = G



+ T , p) (8.87)

+ T , p) = G

+ T , p) − R

∗

T η. (8.88)

Since T  T

we can expand both sides of (8.88) in Taylor’s series retaining

only the linear term:

+ T , p) = G

, p) +

∂

∂T



,p)

T , (8.89)

+ T , p) = G

, p) +

∂

∂T



,p)

T . (8.90)

Substituting these expansions in (8.88) and taking into account (8.86), we obtain

∗

η =



∂

∂T



,p)

−

∂

∂T



,p)



T . (8.91)

Here we also replaced T η by T

η since η has a small value proportional to T .

216 Thermochemistry

As shown in Section 4.8, the temperature derivative of the Gibbs energy at a

constant pressure is minus the entropy. So,

∂

∂T



,p)

=−s

(8.92)

and

∂

∂T



,p)

=−s

(8.93)

where

is the entropy of 1 mol of the solvent and s

is the entropy of 1 mol of

the solvent’s vapor. Then, from (8.91) we obtain

∗

η = (s

− s

)T (8.94)

and

T =

∗

− s

. (8.95)

Multiplying and dividing the right-hand side of the last equation by T

and taking

into account that (

− s

is the amount of heat required to evaporate 1 mol of

the solvent at the boiling point, in other words (

− s

= 

vap

◦

, we obtain

the ﬁnal formula for the elevation of the boiling point T :

T =

∗



vap

◦

(8.96)

Since T is positive, the boiling point of the solution is higher than that of the pure

solvent. The change in the boiling point is proportional to the amount of solute

η.



Example 8.14 What is the change in the boiling temperature of 1 l of water with

15 g of NaCl dissolved in it?

Answer: The molecular weight of NaCl is 58.44 g mol

−1

. Substituting in (8.96) η =

(15/58.44)/(1000/18), R

∗

= 8.31 J K

−1

mol

−1

, T

= 373 K, 

vap

◦

= 40.656

kJ mol

−1

, we obtain T = 0.13 K. 

Example 8.15 Calculate the change in the freezing point of the solution.

Answer: We assume that only pure solvent is frozen, while the solute remains in

the solution. Then the calculation of the freezing point of the solution is similar to

the calculation of the boiling point except we have fusion instead of vaporization.



fus

◦

is the heat released when 1 mol of the solvent is frozen at a temperature T

;