North, Gerald R., Erukhimova Tatiana L. Atmospheric Thermodynamics: Elementary Physics and Chemistry
Подождите немного. Документ загружается.


Notation and abbreviations 217
this heat is negative. Substituting
fus
H
◦
in (8.96), we find that the freezing point
of a solution is lower than that of the pure solvent. The difference T is:
T =−
R
∗
T
2
0
η
|
fus
H
◦
|
. (8.97)
The decrease in the freezing point is proportional to the amount of solute.
Example 8.16 What is the change in the freezing temperature of 1 l of water with
15 g of NaCl dissolved in it?
Answer: |
fus
H
◦
| for water is 6.008 kJ mol
−1
, T
0
=273 K, η =(15/58.44)/
(1000/18), R
∗
= 8.31 J K
−1
mol
−1
. According to (8.97) the change in freezing
temperature T =−0.48 K.
Notes
There are excellent books on physical chemistry, for example Atkins (1994).
The book by Houston (2001) gives a readable account of the kinetic theory of
gases and reaction kinetics. The book by Hobbs (2000) on physical chemistry for
the atmospheric sciences is at about the same level as this book and it delves
much more into the subject of reactions in the atmosphere. A more thorough
discussion of chemical equilibrium is contained in Denbigh (1981). The book on
atmospheric physics and chemistry by Seinfeld and Pandis (1998) is the most
comprehensive. Books on the more general subject of atmospheric chemistry
include those by Brimblecombe (1986) and Warneck (1999). A comprehensive
book on the chemistry of the middle atmosphere is by Brasseur and Solomon (2005).
Finlayson-Pitts and Pitts (2000) cover both the upper and lower atmosphere and
include many useful tables.
Notation and abbreviations for Chapter 8
c speed of light in vacuum (m s
−1
)
G
◦
change in Gibbs energy per mole, at standard conditions
(kJ mol
−1
)
H
◦
change in enthalpy per mole, at standard conditions (kJ mol
−1
)
E
act
activation energy (J)
E energy (J)
η mixing ratio
f frequency of electromagnetic wave (Hz)
F energy flux (J m
−2
s
−1
)
F
λ
(z) flux of electromagnetic energy at wavelength λ, elevation z
(J m
−2
s
−1
m
−1
)

218 Thermochemistry
g, l, aq gaseous, liquid, aqueous phase
h Planck’s constant (J s)
H
◦
standard enthalpy (kJ mol
−1
)
J photodissociation coefficient (s
−1
)
k reaction coefficient
K, K
p
equilibrium constant
K
H
Henry’s Law constant
λ wavelength of an electromagnetic wave (m)
n
0
number density of photons (photons m
−3
)
N (z) concentration of absorbers at level z (molecules m
−3
)
R
∗
universal gas constant (J mol
−1
K
−1
)
σ (λ) absorption cross-section (m
2
)
t
c
lifetime (s)
t
1/2
half life (s)
τ optical depth (dimensionless)
zenith angle
v
∗
threshold velocity to exceed an activation barrier (m s
−1
)
[X ] concentration of X (molecules cm
−3
)
[X ]
0
concentration of X at t = 0
Problems
8.1 Compute the standard enthalpy of reaction for the following reactions:
CO + O
2
→ CO
2
+ O
O + O
3
→ 2O
2
.
Are these reactions exothermic or endothermic?
8.2 Calculate the standard Gibbs energy for the reaction:
NO
3
+ H
2
O → HNO
3
+ OH.
Can this reaction proceed spontaneously?
8.3 Consider the reaction
2NO → N
2
+ O
2
.
Determine whether high or low temperatures are favorable for the forward and reverse
reactions. (Hint: Use formula (8.60).)
8.4 The reaction of HNO
3
dissociation is
HNO
3
+ hf → OH +NO
2
.
By examination of the standard enthalpy find out what photon energy is required for
this reaction to proceed (use Table 8.1).

Problems 219
8.5 Calculate the equilibrium constant at 298 K for the reaction
NO + O
3
→ NO
2
+ O
2
.
Are the reactants or products favored for this reaction at equilibrium at 298 K? Do you
need to raise or lower the temperature to have more products at the equilibrium?
8.6 Find the expression for the equilibrium constant for the reaction
A + B AB,
in terms of reaction coefficients, if the coefficient for the forward reaction is k
1
, and
the coefficient for the reverse reaction is k
2
.
8.7 Estimate the molar solubility of oxygen in water at 25
◦
C and 1 atm. Henry’s constant
for oxygen is 4.4 × 10
9
Pa. The percentage by volume of O
2
in dry air is 20.95%.
8.8 Estimate by how much the amount of nitrogen in a diver’s blood will change when
the diver is rising from a depth of 80 m. An adult human male has an average blood
volume of about 5 l. Use Henry’s Law constant for nitrogen at 25
◦
C, K
H
= 8.68 ×10
9
Pa. (Fast rising, i.e., a rapid decrease in pressure and thus nitrogen solubility, can cause
the formation of nitrogen bubbles in the bloodstream which often leads to death.)
8.9 Show that the difference between the vapor pressure of a solution at a given temperature
T and the vapor pressure of a pure solvent at the same temperature is
p =−
R
∗
T η
v
v
− v
where η is a mole fraction of a nonvolatile solute, v is the volume of 1 mol of a solvent,
v
v
is the volume of 1 mol of vapor. Hint: Suggest that the solution is in equilibrium with
the vapor at pressure e
= e
s
+ p where e
s
is the equilibrium vapor pressure for the
pure solvent and p is small. The fact that p is small allows you to expand the Gibbs
energy in Taylor’s series and retain only the linear term (similar to the calculation of
the boiling point of a solution).

9
The thermodynamic equation
In this chapter we derive two of the fundamental equations of atmospheric science,
the equation of continuity and the thermodynamic equation. The equation of
continuity expresses the conservation of mass in the form of a partial differential
equation, the form needed to implement it in numerical simulations or forecasts.
The thermodynamic equation expresses the combined First and Second Laws of
Thermodynamics into a similar form. But before we come to these important
formulas we need some experience with scalar and vector fields. Much of the chapter
is concerned with elementary vector analysis which should have been covered in
the prerequisite calculus course. Hence, some students can skip over the review
sections, but we advise all students to refresh their memories. All this machinery is
to prepare for the next step in an education in atmospheric sciences: dynamics.
Vector refresher A three-dimensional vector, denoted in boldface, a,isa
mathematical object which has both length and direction. In two-space it can be
represented by an arrow as in Figure 9.1. It takes three numbers to represent a
3-vector, two angles and a length, (θ, φ; |a|). Alternatively, it can be represented by its
three components along the three Cartesian coordinate axes, (a
x
, a
y
, a
z
). Note that the
vector is an abstract object in space independent of the choice of coordinate system,
but the three numbers needed to specify it may individually depend on the coordinate
system chosen by the analyst to describe the vector. For example, it is conventional in
meteorology to set up a Cartesian coordinate system with the origin at a point on the
Earth’s surface, the x-axis increasing in the eastward direction and the y-axis
increasing in the northward direction.
Multiplication by a scalar Let α be a scalar, i.e., a number which is independent of
our choice of coordinate system, a be a vector. Then multiplication of a vector by a
scalar is written as b = αa. The direction of b is the same as that of a and the length is
|α||a|. In other words the two angles designating the direction of b and a are the
220

The thermodynamic equation 221
a
a
x
a
y
Figure 9.1 The vector a in two dimensions.
same, but the length is stretched. If α is negative, the direction of the vector is
reversed. In the case of Cartesian component representation, all three components are
multiplied by α : (αa
x
, αa
y
, αa
z
).
Adding vectors The sum of two vectors is a vector c = a + b whose components
are defined by adding the Cartesian components of the addends:
(c
x
, c
y
, c
z
) = (a
x
+ b
x
, a
y
+ b
y
, a
z
+ b
z
). (9.1)
Clearly a + b = b + a. The sum of the two vectors can also be understood
geometrically by joining the tail of one vector to the head of the other and the line
joining the first tail to the second head is the vector sum.
Cartesian unit vectors A unit vector is a vector which has unit length. It is very
convenient and common to use unit vectors which point along the three Cartesian
axes:
i = (1, 0, 0) (9.2)
j = (0, 1, 0) (9.3)
k = (0, 0, 1). (9.4)
This notation allows us to expand a vector into its Cartesian components
a = a
x
i + a
y
j + a
z
k, or alternatively (a
x
, a
y
, a
z
). (9.5)
The length of a is given by
|a|=
a
2
x
+ a
2
y
+ a
2
z
. (9.6)
Note that the length of a vector is independent of the coordinate system chosen.
Wind in meteorology is usually denoted by v = ui+vj+wk. Thus a wind blowing
to the east is ui;ifu > 0 it is called a westerly. A wind blowing to the north is
vj;
if
v > 0 it is called southerly. Rising air (a vertical wind) is denoted wk. Note that
the components are referred to a Cartesian coordinate system whose origin is at the
surface of the Earth at a fixed location. Wind speed is given by
√
u
2
+ v
2
+ w
2
.
Example 9.1 Find the length of the vector a = 2i + 3j − 4k.
Answer: |a|=
2
2
+ 3
2
+ (−4)
2
=
√
29.

222 The thermodynamic equation
Example 9.2 Find the sum of the vectors a = 2i + 3j − 4k, b =−4i + 3j + 2k.
Answer: a + b =−2i + 6j − 2k.
It is sometimes useful to use a curvilinear coordinate system such as cylindrical
coordinates to describe phenomena in the atmosphere. We use the unit vectors
pointing along the cylindrical coordinate directions (dependent on the point):
ˆ
r,
ˆ
n
θ
,
ˆ
k. A vector a can be written as:
a = a
r
ˆ
r + a
θ
ˆ
n
θ
+ a
z
ˆ
k. (9.7)
Example 9.3 Apurely cyclonic wind blows counterclockwise (northern hemisphere)
about a center of action. At a distance r from the center the wind can be denoted as
v
θ
(r, θ)
ˆ
n
θ
.
Example 9.4 A point on a rotating disk with axis at the disk’s center has velocity
rω
ˆ
n
θ
, where ω is angular velocity in rad s
−1
and r is the axis of rotation.
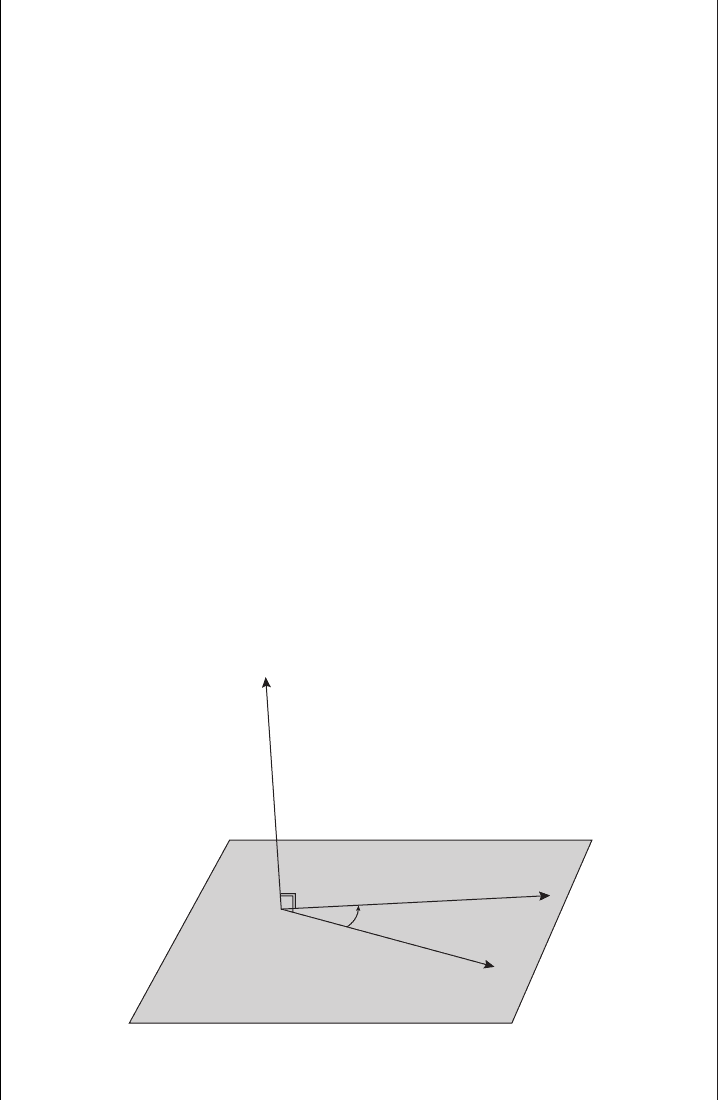
Vector refresher: dot product The dot or scalar product of two vectors results in a
scalar. Even though the components of the two vectors forming the scalar product
depend on the choice of coordinate system, the scalar product does not:
a · b =|a||b|cos(θ
a,b
) (9.8)
where θ
a,b
is the angle between the two vectors as shown in Figure 9.2. Note that
since cos θ
a,b
is an even function of its argument, the order of the vectors in the
product makes no difference: a · b = b · a.
An alternative way to define the dot product a · b is
a · b = a
x
b
x
+ a
y
b
y
+ a
z
b
z
. (9.9)
It can be shown that the two definitions are equivalent. Using the second definition,
b
a
θ
a,b
Figure 9.2 Illustration of the vectors a and b in a dot product.
The thermodynamic equation 223
we can show that c · (a + b) = c ·a + c · b.
It is also clear that i · i = 1, i ·j = 0, etc.
Example 9.5 Find a · b where a = 2i + 3j − 4k, b =−4i + 3j +2k.
Answer: a · b = (2) × (−4) + 3 × 3 + (−4) × (2) =−7.
Example 9.6 What is the angle between a and b?
Answer: cos θ = a · b/|a||b|=−7/ 29; arccos
(
−7/ 29
)
= 1.815.
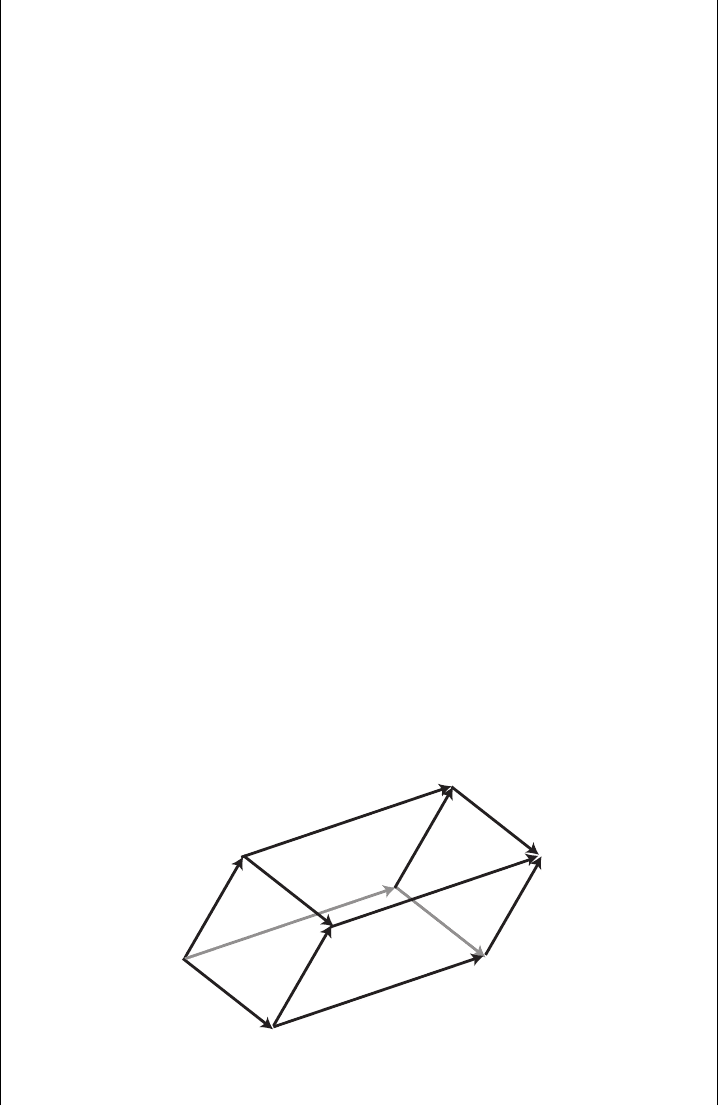
Cross product The vector or cross product is indicated by the notation
c = a × b. (9.10)
The vector c is perpendicular to the plane defined by a and b (see Figure 9.3). The
right hand rule is used to determine its direction (point the right index finger along
the first vector in the product, then sweep it toward the second vector’s direction; the
thumb points in the direction of the vector product). Its length is given by
|c|=|a||b|sin(θ
a,b
). (9.11)
By the right hand rule we see:
a × b =−b ×a. (9.12)
A useful form for the cross product a × b is
c
b
a
θ
a,b
Figure 9.3 Illustration of the vectors c = a × b in a cross product. c is
perpendicular to the plane formed by a and b.
224 The thermodynamic equation
a × b =
ijk
a
x
a
y
a
z
b
x
b
y
b
z
. (9.13)
Math refresher: 3 × 3 determinant Recall that it can be expanded along any row
or column. In the representation of the cross product:
ijk
a
x
a
y
a
z
b
x
b
y
b
z
= i(a
y
b
z
− a
z
b
y
) − j(a
x
b
z
− a
z
b
x
) + k(a
x
b
y
− a
y
b
x
).
Recall the alternating signs of the unit vectors as one expands along the top row. Note
that if two rows (vectors) of a determinant are proportional, the determinant vanishes.
This is simply the statement that sin(θ
a,b
) = 0.
Vector refresher: the box product This is defined by:
a · (b ×c) = c · (a × b) = b · (c × a). (9.14)
A useful form for the box product is
c ·(a × b) =
c
x
c
y
c
z
a
x
a
y
a
z
b
x
b
y
b
z
. (9.15)
The three vectors a, b and c form a rectangular parallelepiped. The box product is the
volume of that geometrical figure. The rules of determinants can be useful here. For
example, cyclic permutation of the rows leads to an equivalent determinant.
Interchanging adjacent rows flips the sign. It is useful to know that the three vectors
a
b
c
Figure 9.4 Sketch of the parallelepiped formed by the vectors a, b and c. The
magnitude of the box product a · b × c is the volume of the parallelepiped.
9.1 Scalar and vector fields 225
of a box product can be identified as the three edges of a solid parallelepiped. The box
product is the volume of the parallelepiped (see Figure 9.4). Note that
k · (i × j) = 1. (9.16)
9.1 Scalar and vector fields
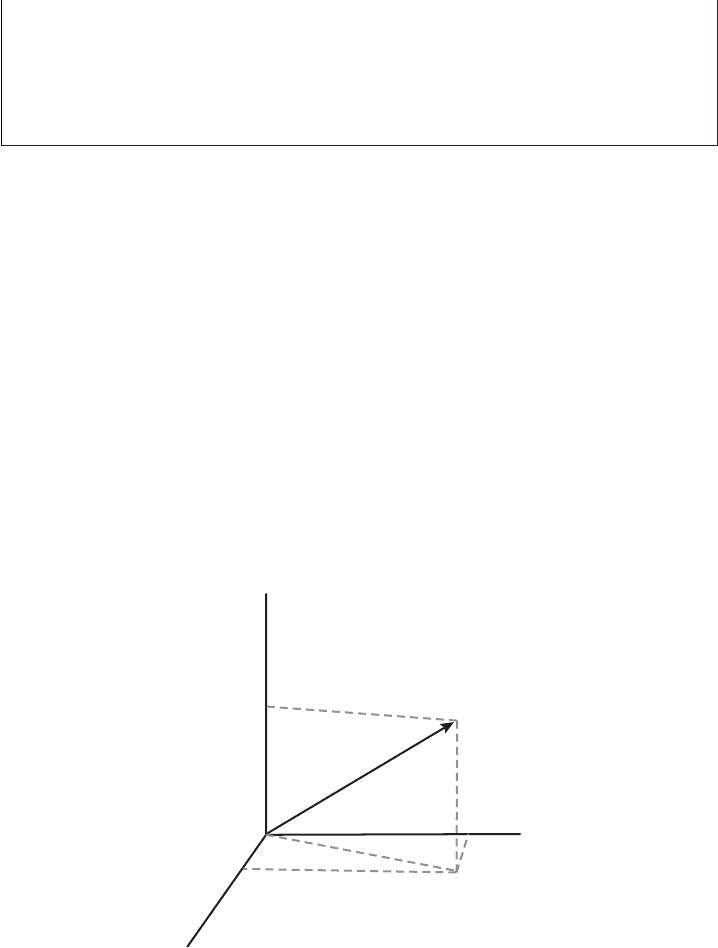
A scalar field is a function defined on the three-dimensional space coordinates and
possibly along the time axis. An example is the temperature field T (x, y, z; t) ≡
T (r, t), where the position vector r is defined by
r ≡ x i + y j + z k (9.17)
and i, j, k are unit vectors pointing along the x, y and z axes (see Figure 9.5). A
small increment in r is denoted as
1
dr = dx i + dy j + dz k. (9.18)
y
x
z
r
x
y
z
Figure 9.5 Schematic diagram of a position vector r whose components are x, y and z.
1
Here we replace the small values x, δx, etc., with infinitesimals dx, etc., with the approximate sign ≈replaced
by the equality sign =. This means that in this notation second-order quantities such as (dx)
2
are neglected (set
to zero) when additive to first-order terms. While this operational shortcut might cause some to cringe, it should
not disturb the flow of our story.

226 The thermodynamic equation
x
y
z
r
d
r
r +dr
Figure 9.6 Schematic diagram of a position vector r and an increment of it dr.
Consider the estimation of the temperature field at the point r + dr (Figure 9.6),
given that we know its value at the point r, namely T (r):
T (r + dr) = T (x + dx, y + dy, z + dz).
We may use the first two terms of the Taylor expansion:
T (x + dx, y + dy, z + dz) = T (x, y, z) +
∂T
∂x
dx +
∂T
∂y
dy +
∂T
∂z
dz. (9.19)
We can also write this as a dot product:
T (r + dr) = T (r) + dr ·∇T (r). (9.20)
After substituting dT = T (r + dr) − T (r), we obtain
dT = dr ·∇T [differential of a scalar field]. (9.21)
The vector ∇T (r) is called the gradient of T. We will use the modern notation ∇T
to denote the gradient (in some older texts it is denoted grad T).
∇T =
∂T
∂x
i +
∂T
∂y
j +
∂T
∂z
k
[gradient of a scalar field]. (9.22)
The gradient is a vector field. At each point in space r it has an associated length
and direction.
