North, Gerald R., Erukhimova Tatiana L. Atmospheric Thermodynamics: Elementary Physics and Chemistry
Подождите немного. Документ загружается.

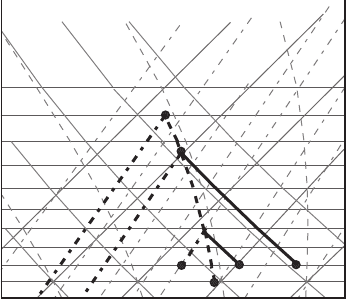
7.3 Chart exercises 177
mb
C
D
B
A
L
1000
900
800
700
600
–10 10 20 C0
2.0 3.0 5.0 10.0 g/kg
Figure 7.12 Diagram for Exercise 10.
draw a moist adiabat starting from L back to the 1000 hPa level. Read the abscissa,
which yields 9
◦
C. With further uplifting, the parcel follows the moist adiabat to
the top of the mountain at the 600 hPa level (point B). At this point the parcel
has saturation mixing ratio equal to 1.6 g kg
−1
. Now we can find the amount of
water condensed out during the ascent to the top of the mountain. It is equal to the
difference between mixing ratios at points A and B, 5 g kg
−1
− 1.6 g kg
−1
=3.4
gkg
−1
. We know that 80% of this moisture, which is 2.7 g kg
−1
, is precipitated
out. Therefore, there is 3.4 g kg
−1
− 2.7 g kg
−1
= 0.7gkg
−1
of liquid water at the
top of the mountain. When descending on the other side of the mountain, the air
parcel follows the moist adiabat again since it is saturated. When descending, the
parcel warms and expands, so water evaporates. Eventually, at some level, all the
liquid water evaporates, the parcel is no longer saturated and its further descent is
along a dry adiabat. How can we can find this “threshold” pressure level when the
parcel reaches its new saturation mixing ratio corresponding to the evaporation of
all liquid water? We know that at the top of the mountain there is 1.6 g of liquid
water per kilogram of dry air. We also know that after the precipitation there is
still 0.7 g of liquid water per kilogram of dry air. Hence, the new saturation mixing
ratio, when all liquid water evaporates, is 1.6 g kg
−1
+0.7 g kg
−1
=2.3 g kg
−1
.
The parcel intersects the line with 2.3 g kg
−1
saturation mixing ratio at the 660 hPa
level (point C). This is the “threshold” pressure level because thereafter the parcel
becomes unsaturated and follows its dry adiabat to the 950 hPa level (point D).
The parcel’s new temperature at point D is 17
◦
C, which is 7
◦
C warmer than in the
beginning. During dry adiabatic descent the mixing ratio is constant, so at point D
the parcel has the same mixing ratio as at point C, which is 2.3 g kg
−1
. The saturation
mixing ratio at point D is 12.6 g kg
−1
. Therefore, the relative humidity of the air
178 Thermodynamic charts
on the other side of the mountain is 18% (compare with 62% at the beginning).
The potential temperature at point D is 294 K (compare with 287 K at point A). The
wet-bulb temperature is again 9
◦
C; it is conserved during the process.
7.4 Stability problem: example sounding
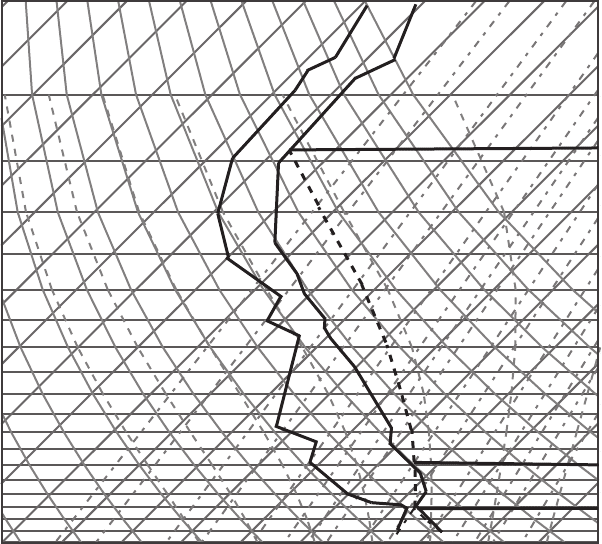
Figure 7.13 shows a typical sounding. In this example the air near the surface
is unsaturated since the dew point is less than the air temperature. When lifted,
the air follows a dry adiabat until it reaches the LCL as depicted in the graph.
Further uplifting is along a moist adiabat (indicated by the dashed line). The first
intersection of this moist adiabat with the sounding curve occurs at the level of free
convection (LFC on the graph). If a parcel is lifted to a height lower than the LFC,
it returns toward the surface because it experiences negative buoyancy since it is
1000
900
800
700
600
500
400
300
200
100
mb
LCL
LFC
LNB
AIR TEMPERATURE
DEW POINT
A
0.1 0.2 0.6 1.0 2.0 3.0 5.0 10.0 20.0 40.0 g/kg
–40 –30 –20 –10 0 10 3020 40 C
Figure 7.13 Illustration of a hypothetical sounding. Solid curves correspond to air
temperature and dew point sounding, the dashed curve shows the actual path of a
parcel lifting from the surface.
7.4 Stability problem: example sounding 179
always cooler than the environment along its path. If, however, the parcel reaches
the LFC, it becomes warmer than its surroundings. So, the LFC is the level where
the parcel becomes positively buoyant. The positive buoyancy carries the parcel up
to the level of neutral buoyancy (LNB), where the parcel’s path intersects with the
(measured) temperature sounding.
In Chapter 6 we discussed stability criteria for an unsaturated parcel. Let us apply
these to different layers of the sounding. By layer we mean a thin slab of air along
the sounding across which there is an approximately constant lapse rate. Consider
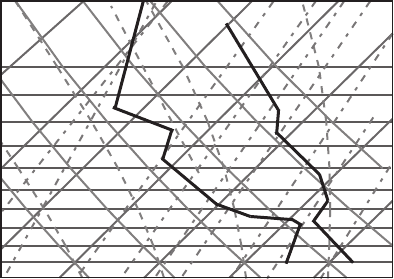
the stability of layers depicted on Figure 7.13 (Figure 7.14 enlarges the part of the
chart we are interested in).
Layer AB is stable since its lapse rate is less than the dry adiabatic lapse rate.
Layer BC is a layer exhibiting a slight inversion. An inversion occurs in a layer
when the temperature increases with height – such a layer is obviously stable. The
layer CD is also stable, its lapse rate being less than the dry adiabatic lapse rate.
The layer DE is neutral; it is parallel to the dry adiabat, so temperature decreases
at the same rate as with a dry adiabatic process.
Now consider the case when the temperature decreases with height at a rate less
than the dry adiabatic lapse rate but greater than the moist adiabatic lapse rate,
d
>>
m
(for example, layer AB). An air parcel in layer AB is negatively
buoyant if lifted a short distance but could become positively buoyant if an
imposed vertical motion is strong enough to bring this parcel to its level of
free convection (LFC). For example, the air might be pushed up a mountainside
or lifted by mechanically induced overturning (turbulence). Such a situation is
called conditional instability. The layer is stable when air is unsaturated, but could
become unstable with externally imposed vertical motion. We can test the layer for
mb
A
B
C
D
E
1000
900
800
700
600
010–10 3020 C
2.0 3.0 5.0 10.0 20.0 g/kg
Figure 7.14 The enlarged area of interest of the sounding shown in Figure 7.13.

180 Thermodynamic charts
conditional instability by calculating the vertical gradient of saturation equivalent
potential temperature dθ
s
/dz, rather than by calculating the lapse rate. In the case of
conditional instability dθ
s
/dz < 0. Indeed, one can see from the graph (Figure 7.14)
that θ
s
(A) >θ
s
(B). If =
m
(A and B are on the same moist adiabat), then θ
s
(A)
= θ
s
(B), and dθ
s
/dz = 0.
To summarize, if the temperature in the particular layer decreases at a rate greater
than the dry adiabatic lapse rate, this layer is unstable in any case for both saturated
and unsaturated parcels. If the temperature decreases at a rate less than the moist
adiabatic lapse rate, this layer is absolutely stable; the saturation equivalent potential
temperature increases with height in this case. The formulas below list the stability
criteria:
>
d
or
dθ
dz
< 0 absolutely unstable, (7.14)
d
> >
m
or
dθ
s
dz
< 0 conditionally unstable, (7.15)
<
m
or
dθ
s
dz
> 0 absolutely stable. (7.16)
There is another type of instability called potential instability. Potential instability
occurs when the layer is lifted as a whole, for example by convection associated
with a moving front or with a flow passing over a mountain. When moving, the
saturation conditions and, consequently, paths are different for the bottom and
top of the layer, which can change the initial temperature gradient. Consider the
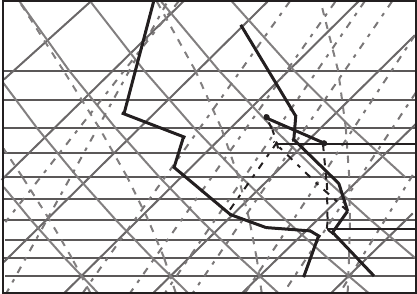
inverted layer BC on the same sounding (Figure 7.15). The reason we chose an
inversion layer is that the effect we want to demonstrate is more pronounced in this
case. Imagine that an uplifting flow moves this layer as a whole 200 hPa higher.
What happens? The bottom of the layer (point B) is almost saturated initially.
Therefore, when lifted, it quickly reaches its LCL (labeled as LCL
B
on the graph)
and follows a moist adiabat thereafter (point B
1
). The situation at the top of the
layer (point C) is different. At the beginning, air at the top of the layer has a low
relative humidity, its dew point is far to the left of its temperature. When uplifted,
the air at point C reaches its LCL (labeled LCL
C
on the graph) and then follows
a moist adiabat (point C
1
). Now consider the lapse rate of the B
1
C
1
layer. It is
larger than the dry adiabatic lapse rate. So, the absolutely stable layer BC becomes
unstable when uplifted. This is the case of potential instability. The criterion
for this instability is a negative gradient of the equivalent potential temperature
in the layer, dθ
e
/dz < 0. Indeed, the equivalent potential temperature remains
constant during the lifting everywhere: both above and below the LCL. When the
air reaches the LCL, the equivalent potential temperature becomes equal to the
saturation equivalent potential temperature, θ
e
= θ
s
. After that, from the criterion
7.5 Convective available potential energy (CAPE) 181
mb
B1
A
B
C
D
C1
LCL_
B
LCL_
C
1000
900
800
700
600
2.0 3.0 5.0 10.0 20.0 g/kg
–10 0 20 3010 C
Figure 7.15 Illustration of potential instability. The stable layer BC becomes
unstable after uplifting.
for conditional instability (7.15) we obtain dθ
e
/dz < 0 for potential instability. One
can see from Figure 7.15 that θ
e
(B)>θ
e
(C). This is a common occurrence in the
southeastern USA as warm moist air is advected from the south, overriding drier
air advected from the west. If lifting occurs, such a configuration can lead to severe
weather conditions.
7.5 Convective available potential energy (CAPE)
In previous sections we analyzed the stability of the displacement of a small parcel
in terms of temperature lapse rate. In this section we will continue to analyze
stability, but in terms of energy. We have already shown that when there is a positive
area in the closed loop between environmental and adiabatic curves on a T –ln p
diagram or, in other words, if a parcel (after a nudge) is positively buoyant, the
parcel’s kinetic energy increases. Consider a parcel being initially unsaturated in
a conditionally unstable atmosphere. We denote the parcel’s initial location by A
in the example of a temperature sounding shown in Figure 7.13. When lifted, the
parcel first follows a dry adiabat until it reaches the LCL. With further lifting, it
follows a moist adiabat. If the upward motion is strong enough to bring the parcel
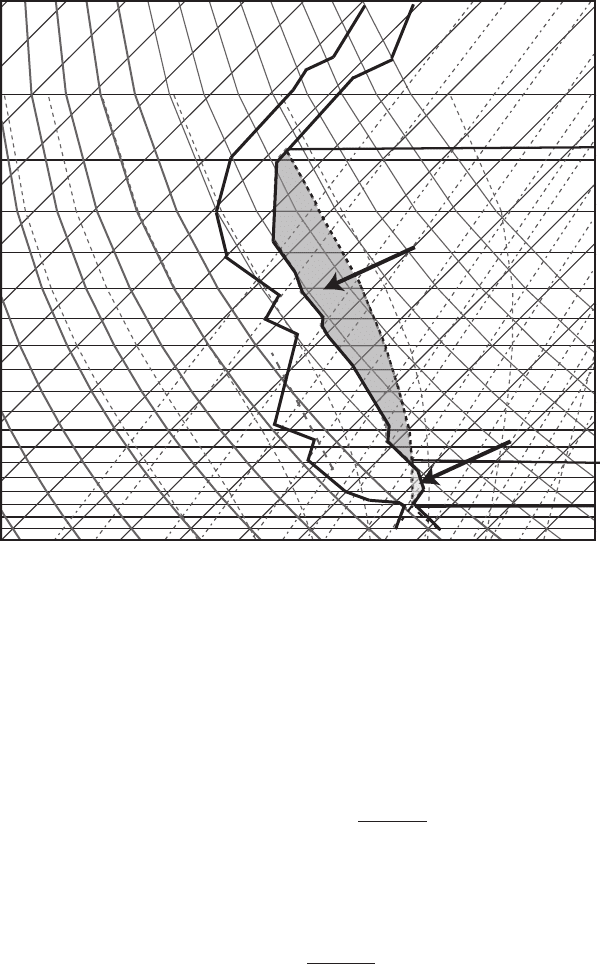
to its LFC, the parcel becomes positively buoyant. Figure 7.16 shows the same
sounding as Figure 7.13. The positive area (shaded dark on Figure 7.16) between
the parcel’s path and the sounding bounded by the LFC and the LNB is called
the convective available potential energy (CAPE). CAPE represents the maximum
kinetic energy that a positively buoyant parcel can acquire by ascending without
exchanging momentum (eddy friction), heat and moisture with its environment.
182 Thermodynamic charts
mb
LCL
LFC
LNB
AIR TEMPERATURE
DEW POINT
CAPE
CIN
1000
900
800
700
600
500
400
300
200
100
0.1 0.2 0.6 1.0 2.0 3.0 5.0 10.0 20.0 40.0 g/kg
–40 –30 –20 –10 0 10 3020 40 C
Figure 7.16 The same sounding as in Figure 7.13. Dark and light gray areas
represent convective available potential energy (CAPE) and convective inhibition
energy (CIN) correspondingly.
We can calculate the ideal change of kinetic energy per unit mass due to positive
buoyancy by integrating (7.5) from LFC to LNB. The amount of kinetic energy
released in this situation is
CAPE =
K =
z
LNB
z
LFC
g
T
a
− T
e
T
e
dz. (7.17)
CAPE is a useful measure of thunderstorm severity, since it allows us to estimate
the value of maximum possible vertical velocity. Indeed, if a parcel has zero vertical
velocity at the LFC, then from (7.17)
w
max
=
√
2CAPE. (7.18)
In this consideration we have neglected the effect of water condensation, which
reduces buoyancy slightly. Values of CAPE greater than 1000 J kg
−1
imply the
possibility of strong convection. Even if the final vertical velocity is less than the
maximum value, the energy is still dissipated in turbulence within the cloud.
7.5 Convective available potential energy (CAPE) 183
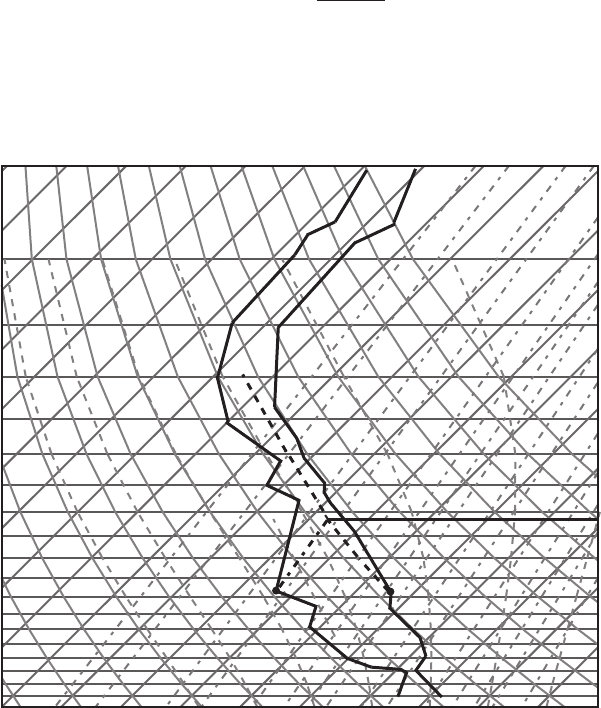
Let us return now to Figure 7.13. Before the parcel starting at point A reaches
its LFC, it has to overcome a potential energy barrier between the LCL and the
LFC, where a parcel is cooler than its environment and negative buoyancy tends
to return the parcel toward the surface. This negative area between the parcel’s
path and environment bounded by the LCL and the LFC is called the convective
inhibition energy (CIN). It is shown as the light gray area in Figure 7.16. CIN
controls whether convection actually occurs. It is a measure of how much energy
is required to overcome the negative buoyancy and allow convection. To find CIN
we have to integrate (7.5) from the LCL to the LFC, namely
CIN =
z
LFC
z
LCL
g
T
a
− T
e
T
e
dz. (7.19)
If the CIN is greater than 100 J kg
−1
, a significant source of lifting is needed to bring
the parcel to its LFC in order to create favorable conditions for deep convection.
mb
LCL
B
AIR TEMPERATURE
DEW POINT
A
1000
900
800
700
600
500
400
300
200
100
0.1 0.2 0.6 1.0 2.0 3.0 5.0 10.0 20.0 40.0 g/kg
–40 –30 –20 –10 0 10 3020 40 C
Figure 7.17 The same sounding as in Figure 7.13. For a parcel originating at point
B, CAPE is zero.

184 Thermodynamic charts
1000
900
800
700
600
500
400
300
200
100
mb
AIR TEMPERATURE
DEW POINT
0.1 0.2 0.6 1.0 2.0 3.0 5.0 10.0 20.0 40.0 g/kg
–40 –30 –20 –10
010 3020 40
C
Figure 7.18 Illustration of a hypothetical sounding.
If we, for example, are interested in the CAPE of an air parcel starting at point B
rather than at point A on the same sounding diagram (Figure 7.17), then the CAPE
is zero. The path of the parcel starting at point B is shown by a dashed line on
Figure 7.17. This parcel is always cooler than its local environment. It is important
to note that the value of CAPE depends on the initial parcel location.
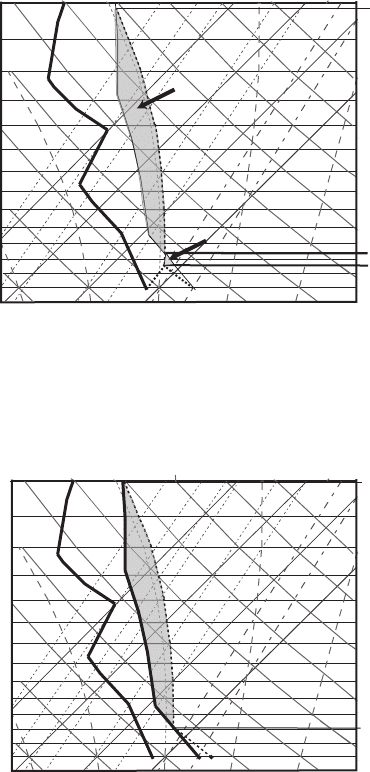
Consider the sounding shown in Figure 7.18. A parcel starting from the surface
will experience negative buoyancy. The area corresponding to the CIN is shown
in light gray in Figure 7.19, which simply enlarges the part of Figure 7.18 we are
interested in. The area shaded in darker gray corresponds to the CAPE. To become
positively buoyant, a parcel started from the surface (point A on the graph) has
to overcome this “light gray” area. Imagine now that we expect the surface to be
warmed in the next couple of hours. Then, instead of point A, the parcel starts from
point A
1
(Figure 7.20). It does not experience negative buoyancy any longer; its LFC
coincides with its LCL, and these are excellent conditions for severe thunderstorm
activity. If, on the contrary, we expect the surface to be cooled (Figure 7.21, point
7.5 Convective available potential energy (CAPE) 185
mb
LCL
LFC
LNB
A
CAPE
CIN
1000
900
800
700
600
500
400
5.0 10.0 20.0 40.0 g/kg
010 3020 40 C
Figure 7.19 The same sounding as in Figure 7.18. CAPE and CIN for the parcel
started from the surface (pointA) are shown in dark and light gray correspondingly.
1000
900
800
700
600
500
400
mb
LCL
LNB
AA1
CAPE
5.0 10.0 20.0 40.0 g/kg
010 3020 40 C
Figure 7.20 The same sounding as in Figure 7.18. Illustration of a hypothetical
surface warming. For the parcel originating at point A
1
, there is no CIN.
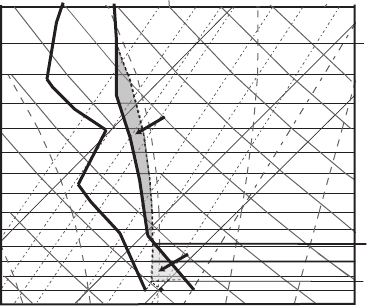
A
2
), then the situation is reversed. CIN becomes larger, and CAPE is smaller than
the previous situation. This means that the conditions for a thunderstorm are no
longer favorable.
Fortunately for the forecaster, the values of many of the parameters discussed
above (CAPE, CIN, etc.) are printed right on the skew T charts that are published at
many sites on the internet. Hence, no tedious computations of areas are necessary
by the user.
186 Thermodynamic charts
mb
LCL
LNB
A
LFC
A2
CAPE
CIN
1000
900
800
700
600
500
400
010 403020 C
5.0 10.0 20.0 40.0 g/kg
Figure 7.21 The same sounding as in Figure 7.18. Illustration of a hypothetical
surface cooling. For the parcel originated from point A
2
, CAPE decreases, but CIN
increases in comparison with the parcel started from A.
Notation and abbreviations for Chapter 7
CAPE convective available potential energy (J kg
−1
)
CIN convective inhibition energy (J kg
−1
)
F, F/
M force, per unit mass (N kg
−1
)
h, u specific enthalpy, internal energy (J kg
−1
)
K kinetic energy (J)
L
evap
latent heat of evaporation (J kg
−1
)
R gas constant (J K
−1
kg
−1
)
ρ
a
parcel density for adiabatic change (kg m
−3
)
ρ
e
environmental density (kg m
−3
)
V
a
, V
e
volumes of a parcel along an adiabat and of the environment (m
3
)
w, w
s
mixing ratio, saturated (g water vapor per kg dry air)
X , Y abscissa, ordinate
Problems
7.1 Refer to the sounding in Figure 7.22.
(a) Estimate the mixing ratio at the surface.
(b) Estimate the saturation mixing ratio at the surface. What is the relative humidity at
the surface?
(c) What is the dew point?
(d) What is the pressure level at the LCL?
(e) What is the wet-bulb temperature at the surface?
(f) Is CIN > 0?
