Невзоров В.Н., Сугак Е.В. Надежность машин и оборудования. Часть 1
Подождите немного. Документ загружается.


141
Ñóùåñòâåííûì ïðåèìóùåñòâîì ýêñïîíåíöèàëüíîãî çàêîíà ÿâëÿåòñÿ òàêæå âîçìîæ-
íîñòü ðàçëîæåíèÿ ôóíêöèè (4.14) èëè (4.15) â ðÿä è àïïðîêñèìàöèè ïðè lt = t/t
0
£
0,1 ëèíåéíîé çàâèñèìîñòüþ âèäà
()
( ) ( )
Pt t
t t
t
t
t
= - + - + » - = -1
2 3
1 1
2 3
0
l
l l
l
! !
...
, (4.16)
êîòîðàÿ ÷àñòî èñïîëüçóåòñÿ ïðè ïðèáëèæåííûõ ðàñ÷åòàõ ïàðàìåòðîâ íàäåæíîñòè.
Âàæíûì ñâîéñòâîì ýêñïîíåíöèàëüíîé ìîäåëè íàäåæíîñòè ÿâëÿåòñÿ òî, ÷òî âåðîÿò-
íîñòü áåçîòêàçíîé ðàáîòû è âåðîÿòíîñòü îòêàçà â èíòåðâàëå âðåìåíè (t,t+Dt) (ò.å.
P(t,t+Dt) è Q(t,t+Dt) = 1–P(t,t+Dt)) çàâèñÿò òîëüêî îò äëèíû ýòîãî èíòåðâàëà Dt è íå
çàâèñÿò îò ïðåäøåñòâóþùåãî âðåìåíè t. Ýòî ñâîéñòâî â çíà÷èòåëüíîé ñòåïåíè îãðàíè-
÷èâàåò âîçìîæíîñòè èñïîëüçîâàíèÿ ýòîé ìîäåëè - îíà ìîæåò ïðèìåíÿòüñÿ òîëüêî â
ñëó÷àÿõ, êîãäà íåîáðàòèìûå èçìåíåíèÿ (ñòàðåíèå) îáúåêòîâ íåñóùåñòâåííû è îòêàçû
ñâÿçàíû òîëüêî ñî ñëó÷àéíûìè âîçäåéñòâèÿìè.
Ýêñïîíåíöèàëüíîå ðàñïðåäåëåíèå ìîæíî îáîáùèòü ðàñïðåäåëåíèåì
Âåéáóëëà â âèäå
P(t) = exp(–lt
a
). (4.17)
 îòëè÷èå îò ýêñïîíåíöèàëüíîãî ðàñïðåäåëåíèå Âåéáóëëà çàäàåòñÿ
äâóìÿ ïàðàìåòðàìè. Ïàðàìåòð l îïðåäåëÿåò ìàñøòàá êðèâîé ðàñïðåäåëå-
íèÿ (ïðè åãî èçìåíåíèè êðèâàÿ ñæèìàåòñÿ èëè ðàñòÿãèâàåòñÿ). Ïðè çíà÷å-
íèè ïàðàìåòðà ôîðìû a<1 ìîäåëü Âåéáóëëà ïîçâîëÿåò îïèñûâàòü ïðèðà-
áîòî÷íûå îòêàçû, îáóñëîâëåííûå ñêðûòûìè äåôåêòàìè, ïðè a=1 - âíåçàï-
íûå îòêàçû â ïåðèîä íîðìàëüíîé ýêñïëóàòàöèè, ïðè 1<a<2 - îòêàçû áûñò-
ðîñòàðåþùèõ îáúåêòîâ, ó êîòîðûõ ïî÷òè íåò ñêðûòûõ äåôåêòîâ, ïðè a>2 -
èçíîñîâûå îòêàçû. Êðîìå òîãî, ïðè a=2 (ðàñïðåäåëåíèå Ðåëåÿ) ìîäåëü
îïèñûâàåò ôóíêöèîíèðîâàíèå îáúåêòà, ñîñòîÿùåãî èç íåñêîëüêèõ ïîñëåäî-
âàòåëüíî ñîåäèíåííûõ äóáëèðîâàííûõ ýëåìåíòîâ (ñì.ãë.5). Îáû÷íî çíà÷å-
íèå a ëåæèò â èíòåðâàëå îò 1 äî 2 [11,16].
Ãàììà-ðàñïðåäåëåíèå
()
( )
( )
Pt t tdt
t
= -
-
ò
l
a
l
a
a
G
1
0
exp (4.18)
èñïîëüçóåòñÿ äëÿ îïðåäåëåíèÿ ìîìåíòà îòêàçà ñ íîìåðîì a ïðè èñïûòàíè-
ÿõ ñ çàìåíîé ýëåìåíòîâ (åñëè íàðàáîòêà ïîä÷èíÿåòñÿ ýêñïîíåíöèàëüíîìó
çàêîíó), à òàêæå äëÿ îïðåäåëåíèÿ îáùåãî ñðîêà ñëóæáû ãðóïïû îáúåêòîâ
ïðè èñïûòàíèÿõ áåç çàìåíû (òàêæå åñëè íàðàáîòêà êàæäîãî èç íèõ ïîä÷è-
íÿåòñÿ ýêñïîíåíöèàëüíîìó çàêîíó) è â íåêîòîðûõ äðóãèõ ñëó÷àÿõ [14].
Îäíèì èç ñàìûõ ïîïóëÿðíûõ â òåîðèè íàäåæíîñòè ÿâëÿåòñÿ íîðìàëü-
íîå ðàñïðåäåëåíèå
() ()
( )
Pt Ft
t
dt
t
= - = - -
-
é
ë
ê
ê
ù
û
ú
ú
-¥
ò
1 1
1
2
2
2
2
s p
m
s
exp . (4.19)
Ôóíäàìåíòàëüíîå çíà÷åíèå íîðìàëüíîãî ðàñïðåäåëåíèÿ ñâÿçàíî ñ öåí-
òðàëüíîé ïðåäåëüíîé òåîðåìîé òåîðèè âåðîÿòíîñòåé (ñì.ãë.2), ñîãëàñíî êî-
òîðîé ðàñïðåäåëåíèå ñóììû ëþáûõ ñëó÷àéíûõ âåëè÷èí â ïðåäåëå ñòðåìèò-
ñÿ ê íîðìàëüíîìó. Íîðìàëüíîå ðàñïðåäåëåíèå ÷àùå âñåãî èñïîëüçóåòñÿ
äëÿ îïèñàíèÿ ïîñòåïåííûõ èçíîñîâûõ îòêàçîâ, îíî îáðàçóåòñÿ, êîãäà íà
ñëó÷àéíóþ âåëè÷èíó äåéñòâóåò áîëüøîå êîëè÷åñòâî ðàâíîïðàâíûõ ôàêòî-

142
ðîâ [14,16]. Åãî íåäîñòàòêîì â íåêîòîðûõ ñëó÷àÿõ ìîæåò îêàçàòüñÿ íàëè÷èå
îáëàñòè îòðèöàòåëüíûõ çíà÷åíèé àðãóìåíòà, ÷òî äëÿ îïèñàíèÿ íàðàáîòêè
íà îòêàç íå èìååò ñìûñëà. Ñ öåëüþ óñòðàíåíèÿ ýòîãî íåäîñòàòêà ìîæíî
âîñïîëüçîâàòüñÿ óñå÷åííûì íîðìàëüíûì ðàñïðåäåëåíèåì
() ()
( )
Pt Ft
c
t
dt
t
= - = - -
-
é
ë
ê
ê
ù
û
ú
ú
ò
1 1
2
2
2
2
0
s p
m
s
exp (4.20)
èëè ëîãàðèôìè÷åñêè íîðìàëüíûì ðàñïðåäåëåíèåì
() ()
( )
Pt Ft
t
t
dt
t
= - = -
-
é
ë
ê
ê
ù
û
ú
ú
ò
1
1
2
1
2
2
2
0
s p
m
s
exp
ln
. (4.21)
Ëîãàðèôìè÷åñêè íîðìàëüíîå ðàñ-
ïðåäåëåíèå ìîæåò òàêæå èñïîëüçî-
âàòüñÿ äëÿ îïèñàíèÿ äîëãîâå÷íîñòè
ìåòàëëîâ, èçíîñîâûõ îòêàçîâ ìàòå-
ðèàëîâ, ñòàðåíèÿ ýëåêòðîííîé àïïà-
ðàòóðû, ïðîöåññîâ âîññòàíîâëåíèÿ
íåêîòîðûõ îáúåêòîâ è ò.ä. [14,16].
Ïðè îïèñàíèè íàäåæíîñòè èñ-
ïîëüçóþòñÿ òàêæå ìîäåëè, îáúåäè-
íÿþùèå íåñêîëüêî ðàñïðåäåëåíèé.
Íàïðèìåð, åñëè îòêàçû îáúåêòà ïðî-
èñõîäÿò ïîä äåéñòâèåì äâóõ íåçàâèñèìûõ ôàêòîðîâ, ïðèâîäÿùèõ ê îòêàçàì
ïî ýêñïîíåíöèàëüíîìó è íîðìàëüíîìó çàêîíàì, òî ðåçóëüòèðóþùàÿ ìîäåëü
áóäåò ïðåäñòàâëÿòü ñîáîé êîìïîçèöèþ (ïðîèçâåäåíèå) ýòèõ ðàñïðåäåëåíèé:
() ( )
Pt t
t
= - -
-
æ
è
ç
ö
ø
÷
é
ë
ê
ù
û
ú
exp l
m
s
1Ô . (4.22)
Äëÿ òîãî ÷òîáû ïîëó÷èòü òåîðåòè÷åñêîå ðàñïðåäåëåíèå, áëèçêîå ê ýêñ-
ïåðèìåíòàëüíîìó, èíîãäà ïëîòíîñòü ðàñïðåäåëåíèÿ íàðàáîòêè äî îòêàçà
èëè ìåæäó îòêàçàìè óäîáíî ïðåäñòàâèòü â âèäå ñóììû (ñìåñè) íåñêîëüêèõ
ðàñïðåäåëåíèé (ñì.ðàçä.2.2) [11]
() ()
ft cft
ii
i
n
=
=
å
1
, (4.23)
ãäå f
i
(t) - i-å òåîðåòè÷åñêîå ðàñïðåäåëåíèå; c
i
- âåñîâîé êîýôôèöèåíò i-ãî ðàñïðåäåëå-
íèÿ (î÷åâèäíî
c
i
i
n
=
å
=
1
1
).
Íàïðèìåð, äëÿ ñóììû (ñóïåðïîçèöèè) äâóõ ýêñïîíåíöèàëüíûõ ðàñïðåäåëåíèé
f(t) = c
1
l
1
exp(–l
1
t) + c
2
l
2
exp(–l
2
t). (4.24)
Ïðè ýòîì âåðîÿòíîñòü áåçîòêàçíîé ðàáîòû, èíòåíñèâíîñòü îòêàçîâ è ñðåäíÿÿ íàðàáîòêà
()
( ) ( )
()
(
)
(
)
( ) ( )
Ptc tc t t
c tc t
c tc t
T
ññ
c
= - + - =
-
+
-
- + -
= +
1 1 2 2
11 1 22 2
1 1 2 2
1
1
2
2
exp exp
exp exp
exp exp
ð
l l l
l
l
l
l
l l l l
, ,
. (4.25)
Ïðè ìàëûõ t çíà÷åíèÿ exp(–l
1
t) è exp(–l
2
t) ìàëû è l(t)»c
1
l
1
+c
2
l
2
. Åñëè, íàïðè-
ìåð, l
2
>l
1
, òî ïðè t®¥ â ôîðìóëàõ (4.24) è (4.25) ÷ëåíû, ñîäåðæàùèå exp(–l
2
t), ìà-
ëû è l(t)®l
1
(ðèñ.4.3).
l
l
1
t
c
1
l
1
+c
2
l
2
Ðèñ.4.3. Ãðàôèê èçìåíåíèÿ èíòåíñèâíîñòè
îòêàçîâ äëÿ ñóììû äâóõ ýêñïîíåíöèàëüíûõ
ðàñïðåäåëåíèé (
l
2
>
l
1
)
143
4.2. Вероятностные модели отказов элементов
Âûáîð àäåêâàòíîé âåðîÿòíîñòíîé ìîäåëè íàäåæíîñòè ýëåìåíòîâ âîç-
ìîæåí íà îñíîâàíèè àíàëèçà ôèçè÷åñêèõ ïðîöåññîâ, ïðîèñõîäÿùèõ â îáú-
åêòå ïðè åãî ýêñïëóàòàöèè. Ïîýòîìó, õîòÿ âòîðîé ýòàï îïðåäåëåíèÿ ïîêà-
çàòåëåé íàäåæíîñòè (îöåíêà ïàðàìåòðîâ ìîäåëè) ïðåäóñìàòðèâàåò ïðîâåð-
êó àäåêâàòíîñòè ìîäåëè ïî ýêñïåðèìåíòàëüíûì äàííûì, êðèòåðèè ñîãëàñèÿ
íå âñåãäà ïîçâîëÿþò îäíîçíà÷íî âûáðàòü ìîäåëü.  ðÿäå ñëó÷àåâ äëÿ ýòî-
ãî, ïðåæäå âñåãî, íåîáõîäèìî ó÷èòûâàòü ôèçè÷åñêóþ ïðèðîäó îòêàçîâ è
õàðàêòåð òå÷åíèÿ ôèçè÷åñêèõ ïðîöåññîâ.
Äëÿ îöåíêè íàäåæíîñòè ðàçëè÷íûõ ïî íàçíà÷åíèþ ýëåìåíòîâ ìîãóò
áûòü ðàññìîòðåíû ìîäåëè îòêàçîâ äâóõ îñíîâíûõ òèïîâ: "íàãðóçêà - ïðî÷-
íîñòü" (ïðî÷íîñòíàÿ íàäåæíîñòü) è "ïàðàìåòð - ïîëå äîïóñêà" (ïàðà-
ìåòðè÷åñêàÿ íàäåæíîñòü).  îáîèõ ñëó÷àÿõ ýëåìåíò ñ÷èòàåòñÿ ðàáîòî-
ñïîñîáíûì, ïîêà åãî îñíîâíûå õàðàêòåðèñòèêè (îïðåäåëÿþùèå ïàðàìåòðû)
â ïðîöåññå ýêñïëóàòàöèè íå äîñòèãíóò ïðåäåëüíûõ çíà÷åíèé (ãðàíèö ðàáî-
÷åé îáëàñòè) è ìåæäó ìîäåëÿìè ýòèõ äâóõ âèäîâ èìåþòñÿ òîëüêî ìåòîäî-
ëîãè÷åñêèå ðàçëè÷èÿ [10]. Îäíàêî åñëè â ïåðâîì ñëó÷àå èìåþò ìåñòî â îñ-
íîâíîì âíåçàïíûå îòêàçû (ïðàêòè÷åñêè ìãíîâåííîå íàðóøåíèå ðàáîòîñïî-
ñîáíîñòè), òî âî âòîðîì - â îñíîâíîì ïîñòåïåííûå (äîñòàòî÷íî ïëàâíîå
"ñïîëçàíèå" ïàðàìåòðîâ ê ãðàíèöå äîïóñòèìûõ çíà÷åíèé).
4.2.1. Прочностная надежность (модель внезапных отказов)
Ïðî÷íîñòü - ñâîéñòâî ìàòåðèàëà ýëåìåíòà ñîïðîòèâëÿòüñÿ ðàçðóøåíèþ
èëè èçìåíåíèþ ôîðìû è ñâîéñòâ ïîä äåéñòâèåì âíåøíèõ èëè âíóòðåííèõ
íàãðóçîê ðàçëè÷íîé ôèçè÷åñêîé ïðèðîäû è ñîõðàíÿòü â çàäàííûõ ïðåäåëàõ
çíà÷åíèÿ âñåõ õàðàêòåðèñòèê [17,18]. Ïàðàìåòðàìè ïðî÷íîñòè ÿâëÿþòñÿ
ïðåäåëû ïðî÷íîñòè (ìåõàíè÷åñêîé, ýëåêòðè÷åñêîé, òåïëîâîé è ò.ä.), ïðåäå-
ëû òåêó÷åñòè, ïîëçó÷åñòè, âûíîñëèâîñòè è äðóãèå õàðàêòåðèñòèêè ìàòå-
ðèàëîâ. Îòêàçû ïî ïàðàìåòðàì ïðî÷íîñòè ìîãóò áûòü ñâÿçàíû ñ ðàçðóøå-
íèåì ýëåìåíòà, íåäîïóñòèìûìè äåôîðìàöèÿìè èëè ðåçêèì èçìåíåíèåì ìå-
õàíè÷åñêèõ, ýëåêòðè÷åñêèõ, òåïëîâûõ è äðóãèõ ñâîéñòâ ìàòåðèàëà âñëåä-
ñòâèå äåôåêòîâ ìàòåðèàëà èëè â ðåçóëüòàòå îäíîêðàòíûõ èëè ìíîãîêðàò-
íûõ ñòàòè÷åñêèõ èëè äèíàìè÷åñêèõ ïåðåãðóçîê [19].
Íàäåæíîñòü ïî ïàðàìåòðàì ïðî÷íîñòè (ïðî÷íîñòíàÿ íàäåæíîñòü)
- ñâîéñòâî ýëåìåíòà ñîõðàíÿòü ðàáîòîñïîñîáíîå ñîñòîÿíèå ïîä âîçäåéñòâè-
åì âíåøíèõ íàãðóçîê. Ïîêàçàòåëÿìè íàäåæíîñòè ïî ïàðàìåòðàì ïðî÷íîñòè
ìîãóò áûòü ñðåäíÿÿ íàðàáîòêà äî îòêàçà èëè âåðîÿòíîñòü áåçîòêàçíîé ðà-
áîòû ýëåìåíòà. Ïîêàçàòåëè ïðî÷íîñòíîé íàäåæíîñòè îïðåäåëÿþòñÿ â çàâè-
ñèìîñòè îò ïðèíÿòûõ êðèòåðèåâ ïðåäåëüíîãî ñîñòîÿíèÿ. Êðèòåðèÿìè ïðå-
äåëüíîãî ñîñòîÿíèÿ ïî ïàðàìåòðàì ïðî÷íîñòè ìîãóò áûòü îïðåäåëåííîå
÷èñëî öèêëîâ íàãðóæåíèÿ èëè íàêîïëåíèå îïðåäåëåííîé âåëè÷èíû îñòà-
òî÷íûõ èçìåíåíèé ïàðàìåòðîâ, äðóãèå õàðàêòåðèñòèêè ýëåìåíòà.
 îáùåì ñëó÷àå îòêàç ýëåìåíòà ïî ïàðàìåòðàì ïðî÷íîñòè âîçíèêàåò
òîãäà, êîãäà óðîâåíü âíåøíèõ âîçäåéñòâèé (ìåõàíè÷åñêèõ, òåïëîâûõ, ýëåê-
òðè÷åñêèõ è ò.ä.) ïðåâûñèò çàïàñ åãî ïðî÷íîñòè. Ïðè ýòîì âíåçàïíûå îò-
êàçû ÿâëÿþòñÿ ñëåäñòâèåì òîãî, ÷òî îòäåëüíûå ýëåìåíòû èìåþò çàïàñ
144
ïðî÷íîñòè íèæå äîïóñòèìîãî è íå ìîãóò ïðîòèâîñòîÿòü ñëó÷àéíûì âñïëå-
ñêàì íàãðóçîê, âîçíèêàþùèì â ðåàëüíûõ óñëîâèÿõ ýêñïëóàòàöèè. Ïîñòå-
ïåííûå îòêàçû ïðîèñõîäÿò â ðåçóëüòàòå óìåíüøåíèÿ ïðî÷íîñòè ýëåìåíòà
(ìåõàíè÷åñêîé, òåïëîâîé, ýëåêòðè÷åñêîé è ò.ä.) âñëåäñòâèå åñòåñòâåííûõ
ïðîöåññîâ ñòàðåíèÿ èëè èçíîñà ìàòåðèàëîâ.
Îöåíêà íàäåæíîñòè ýëåìåíòîâ òåõíè÷åñêèõ ñèñòåì ñ ó÷åòîì õàðàêòå-
ðèñòèê è îñîáåííîñòåé âíåøíèõ íàãðóçîê è çàïàñà ïðî÷íîñòè è èõ èçìåíå-
íèÿ âî âðåìåíè äîëæíà îòðàæàòü ôèçè÷åñêóþ ñóùíîñòü ïðîöåññîâ è ÿâëå-
íèé, ïðîèñõîäÿùèõ â ýëåìåíòå, è òðåáóåò ãîðàçäî ìåíüøåãî ïî ñðàâíåíèþ
ñî ñòàòèñòè÷åñêèìè ìåòîäàìè îáúåìà âû÷èñëåíèé. Êðîìå òîãî, ïðè òàêîì
ïîäõîäå ïîÿâëÿåòñÿ ãîðàçäî áîëüøå âîçìîæíîñòåé ó÷åòà ñâîéñòâ ýëåìåí-
òîâ, íàãðóçîê è óñëîâèé ðàáîòû, â òîì ÷èñëå ïðè êðàéíå äîïóñòèìûõ ïðå-
äåëüíûõ çíà÷åíèÿõ. Íåñìîòðÿ íà î÷åâèäíûå ïðåèìóùåñòâà òàêîãî ïîäõîäà,
â íàñòîÿùåå âðåìÿ ðàñ÷åò ïðî÷íîñòè ýëåìåíòîâ ÷àñòî ïðîâîäèòñÿ ïî óï-
ðîùåííûì ìåòîäèêàì, èíîãäà ÷èñòî èíòóèòèâíî.
Ïîÿâëåíèå âíåçàïíûõ îòêàçîâ è èçìåíåíèå õàðàêòåðèñòèê ýëåìåíòîâ
òåõíè÷åñêèõ ñèñòåì âñåãäà îáóñëîâëåíî îïðåäåëåííûìè ôèçè÷åñêèìè ïðè-
÷èíàìè. Íàïðèìåð, ðàçðûâ òðîñà èëè ìåõàíè÷åñêîå ðàçðóøåíèå äåòàëè ÿâ-
ëÿþòñÿ ñëåäñòâèåì ïðåâûøåíèÿ ïðèëîæåííîé ê íèì íàãðóçêè äîïóñòèìîé
ïðî÷íîñòè, ýëåìåíòû ðàäèîýëåêòðîííîé àïïàðàòóðû ìîãóò ïîòåðÿòü ðàáî-
òîñïîñîáíîñòü âñëåäñòâèå ïåðåãðóçêè (êîðîòêîãî çàìûêàíèÿ, ïîðûâà öåïè,
ðåçêîå èçìåíåíèå ïàðàìåòðîâ ýëåìåíòà è ò.ä.). Ïîýòîìó ïðè ïðîåêòèðîâà-
íèè è èçãîòîâëåíèè òåõíè÷åñêèõ óñòðîéñòâ âñåãäà ñòðåìÿòñÿ îáåñïå÷èòü
äîñòàòî÷íûé çàïàñ ðàáîòîñïîñîáíîñòè (ðàçíîñòü ìåæäó äîïóñòèìîé äëÿ
äàííîãî ýëåìåíòà ïðî÷íîñòüþ è ïðèëîæåííîé ê íåìó íàãðóçêîé) èëè êî-
ýôôèöèåíò çàïàñà ïðî÷íîñòè (îòíîøåíèå ýòèõ âåëè÷èí).
Íàãðóçêè, êîòîðûå èñïûòûâàþò ýëåìåíòû ðàçëè÷íûõ òåõíè÷åñêèõ ñèñ-
òåì, ìîæíî ðàçäåëèòü íà âíåøíèå è âíóòðåííèå [17]. Âíåøíèå íàãðóçêè
âîçíèêàþò âíå ñàìîãî ýëåìåíòà íåçàâèñèìî îò åãî ôóíêöèîíèðîâàíèÿ è
îïðåäåëÿþòñÿ óñëîâèÿìè ðàáîòû (ìåõàíè÷åñêèìè, êëèìàòè÷åñêèìè, ðàäèà-
öèîííûìè, àêóñòè÷åñêèìè è ò.ä.). Âíóòðåííèå íàãðóçêè âîçíèêàþò â ñà-
ìîì ýëåìåíòå è ñâÿçàíû ñ îøèáêàìè ïðè êîíñòðóèðîâàíèè, ïðîèçâîäñòâå è
ýêñïëóàòàöèè (ëîêàëüíûå íàïðÿæåíèÿ, ïåðåãðåâû, óõîäû ïàðàìåòðîâ, ôè-
çèêî-õèìè÷åñêèå èçìåíåíèÿ â ñòðóêòóðå ýëåìåíòà è ò.ä.). Âíóòðåííèå íà-
ãðóçêè çàâèñÿò êàê îò îñîáåííîñòåé ñòðîåíèÿ è ýêñïëóàòàöèè òåõíè÷åñêèõ
îáúåêòîâ, òàê è îò ïàðàìåòðîâ âíåøíèõ íàãðóçîê. Ñëåäóåò îòìåòèòü, ÷òî
ïðèíàäëåæíîñòü êîíêðåòíûõ óñëîâèé ðàáîòû ýëåìåíòà ê âíåøíèì èëè
âíóòðåííèì íàãðóçêàì îïðåäåëÿåòñÿ ïîñòàíîâêîé çàäà÷è èññëåäîâàíèÿ: íà-
ïðèìåð, èçìåíåíèå òåìïåðàòóðû îêðóæàþùåé ñðåäû - âíåøíÿÿ íàãðóçêà, à
ìåñòíûé ïåðåãðåâ èç-çà îøèáîê â êîíñòðóêöèè - âíóòðåííÿÿ, ìåõàíè÷åñêèå
óñèëèÿ, âîçíèêàþùèå ïðè âçàèìîäåéñòâèè ýëåìåíòîâ ñèñòåìû, äëÿ ñèñòå-
ìû â öåëîì ÿâëÿþòñÿ âíóòðåííèìè íàãðóçêàìè, à äëÿ îòäåëüíîãî ýëåìåíòà
ñèñòåìû - âíåøíèìè è ò.ä.
 ðåàëüíûõ óñëîâèÿõ ïðè èçãîòîâëåíèè è ýêñïëóàòàöèè ïðàêòè÷åñêè
âñåãäà íàáëþäàþòñÿ ðàçáðîñû ôàêòè÷åñêèõ çíà÷åíèé ïðî÷íîñòè, âíåøíèõ
è âíóòðåííèõ íàãðóçîê, ïðî÷íîñòü è íàãðóçêè ÿâëÿþòñÿ âåëè÷èíàìè äîñòà-
òî÷íî ñëó÷àéíûìè. Ýòè ðàçáðîñû ñâÿçàíû ñ îñîáåííîñòÿìè ïðîåêòèðîâà-
145
íèÿ, èçãîòîâëåíèÿ è ïðèìåíåíèÿ ýëåìåíòîâ, ñòðîåíèåì è ñòðóêòóðîé êîí-
ñòðóêöèîííûõ ìàòåðèàëîâ, ìíîãèìè äðóãèìè ïðè÷èíàìè.
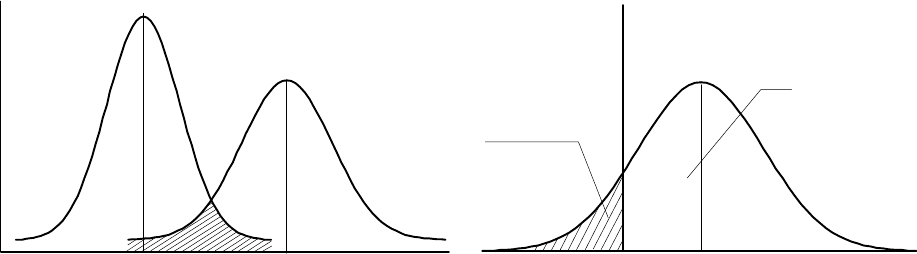
Õàðàêòåðèñòèêè ðàñïðåäåëåíèé ïðî÷íîñòè è íàãðóçêè ìîãóò áûòü ïîëó-
÷åíû àíàëèòè÷åñêèìè èëè ýêñïåðèìåíòàëüíûìè ìåòîäàìè ñ èñïîëüçîâàíè-
åì ìåòîäîâ ìàòåìàòè÷åñêîé ñòàòèñòèêè [20]. Äëÿ íàãëÿäíîñòè êðèâûå
ïëîòíîñòè âåðîÿòíîñòè íàãðóçêè f(S) è ïðî÷íîñòè f(R) óäîáíî ñîâìåñòèòü
íà îäíîì ãðàôèêå (ðèñ.4.4).
Ðàáîòîñïîñîáíîñòü ýëåìåíòà áóäåò îáåñïå÷åíà, åñëè íàãðóçêà íå áóäåò
ïðåâûøàòü íèæíåãî ïðåäåëà äèàïàçîíà ïðî÷íîñòè. Íà ïðàêòèêå ïðè ðàñ÷å-
òàõ ýëåìåíòîâ ðàçëè÷íûõ òåõíè÷åñêèõ ñèñòåì ÷àñòî îãðàíè÷èâàþòñÿ ââå-
äåíèåì êîýôôèöèåíòà çàïàñà ïðî÷íîñòè, êîòîðûé ðàâåí îòíîøåíèþ ìàòå-
ìàòè÷åñêèõ îæèäàíèé (èëè ñðåäíèõ çíà÷åíèé) âåëè÷èí ïðî÷íîñòè è íà-
ãðóçêè: K = M(R)/M(S). Íà ñàìîì äåëå î÷åâèäíî, ÷òî ïðè ñðàâíèòåëüíî
áîëüøîì ðàçáðîñå âîçìîæíûõ çíà÷åíèé âåëè÷èí íàãðóçêè è ïðî÷íîñòè
ñóùåñòâóåò âåðîÿòíîñòü îòêàçà ýëåìåíòà ïî ïàðàìåòðó ïðî÷íîñòè äàæå
ïðè ñðàâíèòåëüíî áîëüøîì çíà÷åíèè êîýôôèöèåíòà çàïàñà ïðî÷íîñòè K.
Ñîñòîÿíèå ýëåìåíòà ïî óñëîâèþ ïðî÷íîñòè ìîæåò ñ÷èòàòüñÿ áåçîòêàç-
íûì, åñëè íàãðóçêà S íå ïðåâûøàåò ïðî÷íîñòè (íåñóùåé ñïîñîáíîñòè)
ýëåìåíòà R (S£R), è òîãäà âåðîÿòíîñòü áåçîòêàçíîé ðàáîòû ýëåìåíòà ïðè
èçâåñòíûõ çàêîíàõ ðàñïðåäåëåíèÿ S è R ðàâíà âåðîÿòíîñòè ýòîãî ñîáûòèÿ:
( ) ( )
P pRS fRdR
i
S
i
= > =
¥
ò
. (4.26)
 îáùåì ñëó÷àå âåðîÿòíîñòü áåçîòêàçíîé ðàáîòû ïðè âñåõ âîçìîæíûõ
çíà÷åíèÿõ íàãðóçêè ìîæåò áûòü îïðåäåëåíà ïî ðàñïðåäåëåíèþ ñëó÷àéíîé
âåëè÷èíû çàïàñà ïðî÷íîñòè L = R–S (ðèñ.4.5), êîòîðàÿ ïðåäñòàâëÿåò ñî-
áîé êîìïîçèöèþ çàêîíîâ ðàñïðåäåëåíèÿ [20]:
( ) ( ) ( )
( ) ( )
PpRS pL fLdL
MRMS
= > = > =
-
¥
ò
0
. (4.27)
Åñëè íàãðóçêà è ïðî÷íîñòü ðàñïðåäåëåíû ïî íîðìàëüíîìó çàêîíó, òî çà-
ïàñ ïðî÷íîñòè (èõ êîìïîçèöèÿ) ðàñïðåäåëåí òàêæå ïî íîðìàëüíîìó çàêîíó
f
(
R
)
f
(
S
)
f
(
R
)
f
(
S
)
M
(
S
)
M
(
R
)
S, R
f
(
L
)
M
(
L
)
L
Q = 1 - P
P
Ðèñ.4.4. Ïëîòíîñòü âåðîÿòíîñòè íàãðóçêè S Ðèñ.4.5. Ïëîòíîñòü âåðîÿòíîñòè
è ïðî÷íîñòè
R
çàïàñà ïðî
÷
íîñòè
L
=
R
–
S
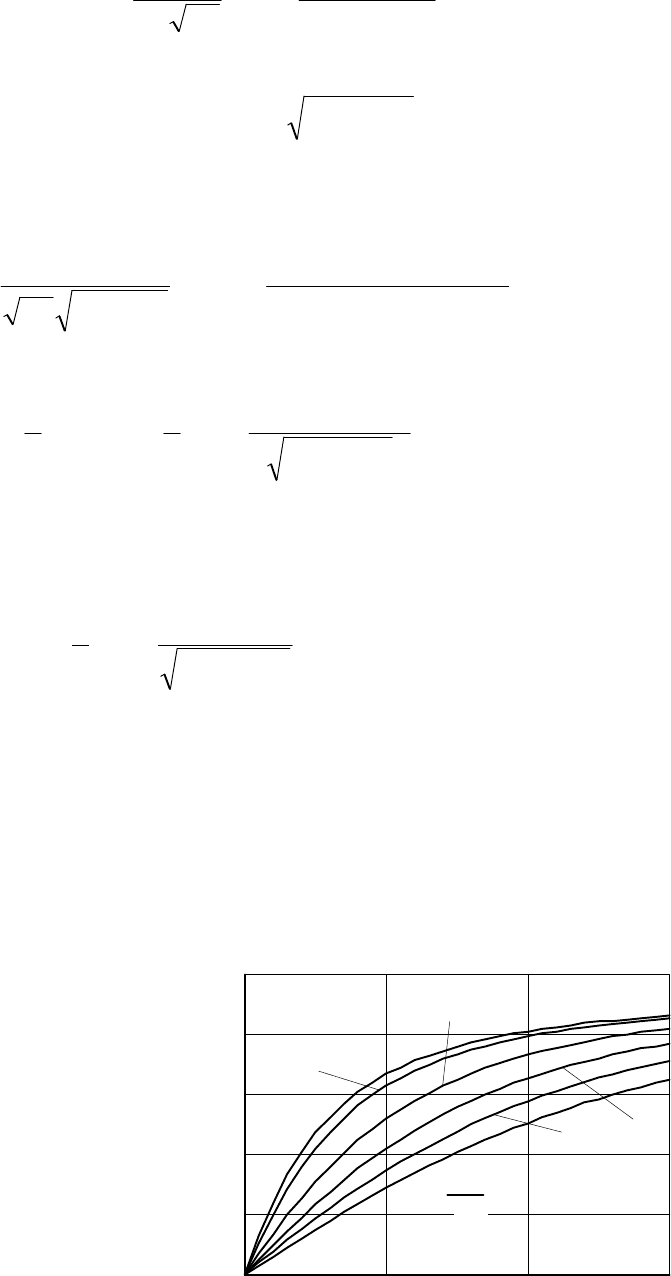
146
( )
( )
( )
fL
LML
L
L
= -
-
é
ë
ê
ê
ù
û
ú
ú
1
2
2
2
2
s p
s
exp (4.28)
ñ ìàòåìàòè÷åñêèì îæèäàíèåì è ñðåäíèì êâàäðàòè÷åñêèì îòêëîíåíèåì
( ) ( ) ( )
ML MR MS
L R S
= - = +, s s s
2 2
, (4.29)
ãäå M(R) è M(S) - ìàòåìàòè÷åñêèå îæèäàíèÿ ïðî÷íîñòè è íàãðóçêè; s
R
è s
S
- èõ ñðåä-
íèå êâàäðàòè÷åñêèå îòêëîíåíèÿ.
Òîãäà âåðîÿòíîñòü áåçîòêàçíîé ðàáîòû îïðåäåëÿåòñÿ ôîðìóëîé
( )
( ) ( )
( )
[
]
( )
PpL
L MR MS
dL
R S
R S
= > =
+
-
- -
+
ì
í
ï
î
ï
ü
ý
ï
þ
ï
¥
ò
0
1
2
2
2 2
2
2 2
0
p s s
s s
exp (4.30)
èëè ñ èñïîëüçîâàíèåì íîðìèðîâàííîé ôóíêöèè Ëàïëàñà Ô(z)
( )
( ) ( )
P Ôz
MR MS
R S
= +
-
+
æ
è
ç
ç
ö
ø
÷
÷
1
2
2 2
=
1
2
+Ô
s s
. (4.31)
Ôîðìóëó ìîæíî çàïèñàòü ÷åðåç êîýôôèöèåíò çàïàñà ïðî÷íîñòè K =
M(R)/M(S) è êîýôôèöèåíòû âàðèàöèè íàãðóçêè v
S
= s
S
/M(S) è ïðî÷-
íîñòè v
R
= s
R
/M(R) [21]:
P
K
Kv v
R S
=
-
+
æ
è
ç
ç
ö
ø
÷
÷
1
2
+ Ô
1
2 2
. (4.32)
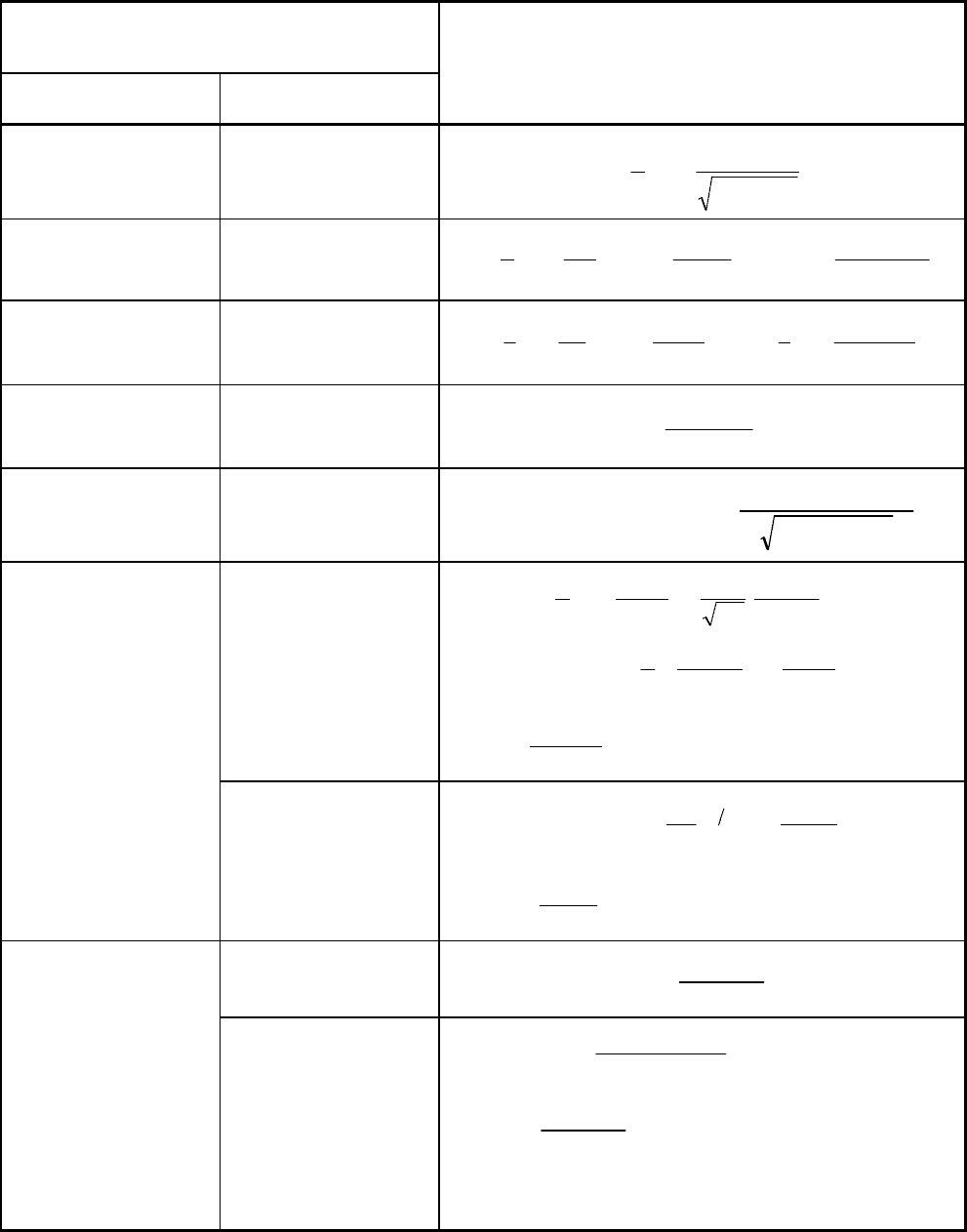
Íà ðèñ.4.6 ïðåäñòàâëåíû ãðàôèêè çàâèñèìîñòè âåðîÿòíîñòè áåç-
îòêàçíîé ðàáîòû ýëåìåíòà ïî ïàðàìåòðàì ïðî÷íîñòè îò çíà÷åíèÿ êîýôôè-
öèåíòà çàïàñà ïðî÷íîñòè ïðè ðàçëè÷íûõ îòíîøåíèÿõ êîýôôèöèåíòîâ âà-
ðèàöèè ðàñïðåäåëåíèé íàãðóçêè è ïðî÷íîñòè.
Ôîðìóëû, àíàëîãè÷íûå ïðèâåäåííûì äëÿ íîðìàëüíûõ çàêîíîâ ðàñïðåäåëåíèÿ, ìîãóò
áûòü ïîëó÷åíû è äëÿ äðóãèõ ñî÷åòàíèé çàêîíîâ ðàñïðåäåëåíèÿ íàãðóçêè è ïðî÷íîñòè. Â
òàáë.4.2 ïðèâåäåíû çàâèñèìîñòè äëÿ ðàñ÷åòà âåðîÿòíîñòè áåçîòêàçíîé ðàáîòû ýëåìåí-
òîâ ïî ïðî÷íîñòè (âåðîÿòíîñòü íåðàçðóøåíèÿ) ïðè ðàçëè÷íûõ ñî÷åòàíèÿõ çàêîíîâ ðàñ-
ïðåäåëåíèÿ ïðî÷íîñòè è íàãðóçêè äëÿ íåêîòîðûõ ïðàêòè÷åñêè çíà÷èìûõ ñëó÷àåâ
[14,16,22].
Äëÿ îáùåãî ñëó÷àÿ ïðè ïðîèçâîëü-
íûõ çàêîíàõ ðàñïðåäåëåíèÿ íàãðóçêè è
ïðî÷íîñòè âåðîÿòíîñòü áåçîòêàçíîé ðà-
áîòû ýëåìåíòà ïî óñëîâèþ ïðî÷íîñòè
îïðåäåëÿåòñÿ ïðèáëèæåííûìè ìåòîäàìè
[20].
Ïðèâåäåííûå ïðîñòåéøèå ìîäåëè
íàäåæíîñòè ïîçâîëÿþò ðàññ÷èòàòü "ñòà-
òè÷åñêóþ" íàäåæíîñòü (âåðîÿòíîñòü áåç-
îòêàçíîé ðàáîòû â äàííûé êîíêðåòíûé
ìîìåíò âðåìåíè) è íå ïîçâîëÿþò ïðî-
ñëåäèòü èçìåíåíèå íàäåæíîñòè âî âðå-
ìåíè. Îäíàêî åñëè èçâåñòíû çàêîíîìåð-
íîñòè èçìåíåíèÿ íàãðóçêè è ïðî÷íîñòè
(ò.å. èçìåíåíèå ïàðàìåòðîâ ðàñïðåäåëå-
íèé), òî â ðàñ÷åòå ìîæíî ó÷åñòü è ôàê-
òîð âðåìåíè.
0,50
0,60
0,70
0,80
0,90
P
1 3
v
S
v
R
= 5
2
4
3
2
1
0,5
n
Ðèñ.4.6. Çàâèñèìîñòü âåðîÿòíîñòè
áåçîòêàçíîé ðàáîòû ýëåìåíòà ïî ïðî÷íîñòè
îò êîýôôèöèåíòà çàïàñà ïðî÷íîñòè (v
R
=0,5)
147
Òàáëèöà 4.2
РАСЧЕТНЫЕ ФОРМУЛЫ ПРОЧНОСТНОЙ НАДЕЖНОСТИ ЭЛЕМЕНТОВ
Çàêîíû ðàñïðåäåëåíèÿ
è ïàðàìåòðû
Ðàñ÷åòíûå ôîðìóëû
ïðî÷íîñòè íàãðóçêè
Íîðìàëüíûé
(R è s
R
2
)
Íîðìàëüíûé
(S è s
S
2
)
P
RS
R S
=
-
+
æ
è
ç
ç
ö
ø
÷
÷
1
2
+Ô
s s
2 2
Ýêñïîíåíöèàëüíûé
(l
S
=1/S)
P Ô
R
R Ô
R
R
SR
S
SR
R
= +
æ
è
ç
ö
ø
÷
- -
æ
è
ç
ö
ø
÷
-
æ
è
ç
ö
ø
÷
1
2 2
2 2 2 2
2
s
ls
l
ls
s
exp
Ýêñïîíåíöèàëüíûé
(l
R
=1/R)
Íîðìàëüíûé
(S è s
S
2
)
P Ô
R
S
S
S
RS
R
RS
S
=
æ
è
ç
ö
ø
÷
- -
æ
è
ç
ö
ø
÷
+
-
æ
è
ç
ö
ø
÷
é
ë
ê
ê
ù
û
ú
ú
1
2 2
1
2
2 2 2 2
2
+ Ô
s
ls
l
ls
s
exp
Ãàììà
(l
S
è a
S
)
P
S
S R
S
=
+
æ
è
ç
ö
ø
÷
l
l l
a
Ëîãàðèôìè÷åñêè-
íîðìàëüíûé
(M[lnR] è s
2
lnR
)
Ëîãàðèôìè÷åñêè-
íîðìàëüíûé
(M[lnS] è s
2
lnS
))
( )
[
]
[
]
P zdz z
M R M S
z
R S
= - =
-
+
¥
ò
j
s s
,
ln ln
ln ln
ãäå
2 2
Âåéáóëëà
(a
R
, b
R
è R)
Íîðìàëüíûé
(S è s
S
2
)
P
RS
a R
y
a R
y
RS
dy
S
R
S
b
R
R
S S
=+
-
æ
è
ç
ö
ø
÷
-
-
æ
è
ç
ö
ø
÷
´
´ - -
-
æ
è
ç
ö
ø
÷
é
ë
ê
ì
í
ï
î
ï
+
-
ù
û
ú
ü
ý
ï
þ
ï
¥
ò
1
2
1
2
1
2
0
2
Ô
s
p
s
s s
exp
ãäå
y
S R
a R
R
=
-
-
Âåéáóëëà
(a
S
, b
S
è S)
P y
a
a
y
RS
a
dy
R
S
b
S
R
S
b
=- - +
-
æ
è
ç
ö
ø
÷
é
ë
ê
ê
ù
û
ú
ú
¥
ò
1
1
0
exp
ãäå
y
SR
a
R
b
R
=
-
æ
è
ç
ö
ø
÷
Ãàììà
(l
R
è a
R
)
Ýêñïîíåíöèàëüíûé
(l
S
=1/S)
P
R
S R
R
=-
+
æ
è
ç
ö
ø
÷
1
l
l l
a
Ãàììà
(l
S
è a
S
)
(
)
( ) ( )
( )
P
R S
R S
z R S
=
+
G
G G
B
a
a
a a
a a,
ãäå
z
S
S R
=
+
l
l l
,
( ) ( )
B
z
p
q
z
pq z z dz, = -
-
-
ò
1
1
0
1
-
íåïîëíàÿ (óñå÷åííàÿ) áåòà-ôóíêöèÿ.
Ïðèìå÷àíèå:  òàáëèöå äëÿ êðàòêîñòè ïðèíÿòû îáîçíà÷åíèÿ R=M(R) è S=M(S).

148
Íàïðèìåð, åñëè â ôîðìóëå (4.30) M(R)=R(t), s
R
=s
R
(t) è M(S)=S(t), s
S
=s
S
(t), òî
()
() ()
() ()
Pt
Rt St
t t
R S
=
-
+
é
ë
ê
ê
ù
û
ú
ú
1
2
+Ô
s s
2 2
(4.33)
è âåðîÿòíîñòü áåçîòêàçíîé ðàáîòû ñòàíîâèòñÿ ôóíêöèåé âðåìåíè. Â ïîäîáíîì âèäå
ìîæíî ïðåäñòàâèòü è ôîðìóëû äëÿ äðóãèõ çàêîíîâ ðàñïðåäåëåíèÿ.
Âåðîÿòíîñòíûå ðàñ÷åòû ïðî÷íîñòè ïîçâîëÿþò ó÷åñòü ñëó÷àéíûé õàðàê-
òåð íàãðóçîê è ñâîéñòâ ýëåìåíòîâ, ïåðåéòè îò îöåíêè ïðî÷íîñòè ïî êîýô-
ôèöèåíòàì çàïàñà ê îöåíêå âåðîÿòíîñòè áåçîòêàçíîé ðàáîòû è ïðîãíîçèðî-
âàíèþ ðåñóðñà [20]. Îäíàêî èñïîëüçîâàíèå âåðîÿòíîñòíûõ êðèòåðèåâ è ïî-
ëó÷åíèå äîïîëíèòåëüíîé èñõîäíîé èíôîðìàöèè î ïðî÷íîñòè è íàãðóçêàõ
çíà÷èòåëüíî óñëîæíÿþò ðàñ÷åò. Ïîýòîìó ïåðåä ïðîâåäåíèåì ðàñ÷åòîâ öå-
ëåñîîáðàçíî îãðàíè÷èòü íîìåíêëàòóðó ýëåìåíòîâ (äåòàëåé, óçëîâ, êîíñò-
ðóêöèé è ò.ä.), äëÿ êîòîðûõ âåðîÿòíîñòíûé ðàñ÷åò íåîáõîäèì. Ê ÷èñëó òà-
êèõ ýëåìåíòîâ ìîæíî îòíåñòè ýëåìåíòû, íàäåæíîñòü êîòîðîé ëèìèòèðóåò
íàäåæíîñòü âñåé ñèñòåìû, ýëåìåíòû ñ íåáîëüøèìè êîýôôèöèåíòàìè çàïà-
ñà ïðî÷íîñòè (çàïàñ ïðî÷íîñòè ìîæíî ñ÷èòàòü äîñòàòî÷íûì, åñëè âûïîë-
íÿåòñÿ óñëîâèå
`
R –
`
S ³ 3(s
R
+s
S
), ïðè ýòîì âåðîÿòíîñòü áåçîòêàçíîé ðà-
áîòû P > 0,999), ýëåìåíòû, èñïûòûâàþùèå íàãðóçêè ñ øèðîêèì äèàïàçî-
íîì çíà÷åíèé, ýëåìåíòû ñ íåñòàáèëüíûìè ñâîéñòâàìè è õàðàêòåðèñòèêàìè
ïðî÷íîñòè (íàïðèìåð, äëÿ êîíñòðóêöèîííûõ ìàòåðèàëîâ êîýôôèöèåíòû âà-
ðèàöèè ïðî÷íîñòè v
R
: äëÿ îáû÷íûõ ñòàëåé è òèòàíîâûõ ñïëàâîâ - 0,02-
0,06, äëÿ óëó÷øåííûõ èëè íîðìàëèçîâàííûõ ñòàëåé - 0,03-0,04, äëÿ ñòàëåé
ñ òåðìè÷åñêè óïðî÷íåííîé ïîâåðõíîñòüþ - 0,05-0,07, äëÿ àëþìèíèåâûõ
ñïëàâîâ - 0,014-0,070, äëÿ îñòàëüíûõ ìàòåðèàëîâ â îòñóòñòâèå ñâåäåíèé -
0,07-0,1, äëÿ äåòàëåé, èçãîòîâëåííûõ ëèòüåì, - â 3-5 ðàç áîëüøå [14,21,23]).
Ïðèìåð 4.1.  êà÷åñòâå ïðèìåðà ðàññìîòðèì ðàñ÷åò ïðî÷íîñòè îäíîé èç äåòàëåé
äâèãàòåëÿ âíóòðåííåãî ñãîðàíèÿ [14]. Ïóñòü íàãðóçêè, êîòîðûå îíà èñïûòûâàåò, âûçû-
âàþò íàïðÿæåíèå, ðàñïðåäåëåííîå ïî íîðìàëüíîìó çàêîíó ñ ìàòåìàòè÷åñêèì îæèäàíè-
åì M(S) =
`
S = 410 ÌÏà è ñðåäíèì êâàäðàòè÷åñêèì îòêëîíåíèåì s
S
= 100 ÌÏà.
Ïðî÷íîñòü (ïðåäåëüíî äîïóñòèìîå íàïðÿæåíèå) ìàòåðèàëà äåòàëè èìååò òàêæå íîð-
ìàëüíîå ðàñïðåäåëåíèå ñ ìàòåìàòè÷åñêèì îæèäàíèåì M(R) =
`
R = 830 ÌÏà è ñðåäíèì
êâàäðàòè÷åñêèì îòêëîíåíèåì s
R
= 70 ÌÏà. Ïðè ðàáîòå äâèãàòåëÿ â óñëîâèÿõ Êðàéíåãî
Ñåâåðà ìàòåìàòè÷åñêîå îæèäàíèå ïðî÷íîñòè íå èçìåíÿåòñÿ, à ñðåäíåå êâàäðàòè÷åñêîå
îòêëîíåíèå óâåëè÷èâàåòñÿ â äâà ðàçà (s¢
R
= 140 ÌÏà).
Î÷åâèäíî, êîýôôèöèåíò çàïàñà ïðî÷íîñòè â îáîèõ ñëó÷àÿõ (äëÿ íîðìàëüíûõ óñëî-
âèé è óñëîâèé Êðàéíåãî Ñåâåðà) áóäåò îäèí è òîò æå: K =
`
R/
`
S = 830/410 = 2,02.
Îäíàêî âåðîÿòíîñòü áåçîòêàçíîé ðàáîòû (ôîðìóëà (4.31)) âî âòîðîì ñëó÷àå áóäåò ñó-
ùåñòâåííî ìåíüøå:
( )
( )
P Ô Q P
P Ô Q P
=
-
+
æ
è
ç
ö
ø
÷
= + = = - =
¢
=
-
+
æ
è
ç
ö
ø
÷
= + =
¢
= -
¢
=
1
2
+ ,
1
2
+ ,
Ô , , , ,
Ô , , , .
830 410
70 100
1
2
344 09997 1 00003
830 410
140 100
1
2
244 09925 1 00075
2 2
2 2
Òàêèì îáðàçîì, äàæå ïðè ñðàâíèòåëüíî áîëüøîì êîýôôèöèåíòå çàïàñà ïðî÷íîñòè
(Ê > 2) ñóùåñòâóåò âåðîÿòíîñòü îòêàçà äåòàëè, ïðè÷åì âî âòîðîì ñëó÷àå âåðîÿòíîñòü
îòêàçà óâåëè÷èâàåòñÿ â 25 ðàç ïî ñðàâíåíèþ ñ ïåðâûì.
Ïðèâåäåííûé ïðèìåð ïîêàçûâàåò íåîáõîäèìîñòü è âàæíîñòü âåðîÿòíîñòíûõ ðàñ÷å-
òîâ ïðî÷íîñòíîé íàäåæíîñòè, îñîáåííî äëÿ îòâåòñòâåííûõ ýëåìåíòîâ è ýëåìåíòîâ, ðà-
áîòàþùèõ â ýêñòðåìàëüíûõ óñëîâèÿõ.
149
4.2.2. Параметрическая надежность (модель постепенных отказов)
 ìîäåëÿõ òèïà "ïàðàìåòð - ïîëå äîïóñêà" (êóìóëÿòèâíûõ ìîäåëÿõ
[24]) ðàññìàòðèâàåòñÿ ðåçóëüòàò äåéñòâèÿ íàãðóçîê â âèäå èçìåíåíèé ôè-
çè÷åñêèõ ïàðàìåòðîâ ýëåìåíòîâ òåõíè÷åñêèõ ñèñòåì. Êàæäûé ýëåìåíò
ìîæíî õàðàêòåðèçîâàòü êàêèì-ëèáî îïðåäåëÿþùèì ïàðàìåòðîì Õ, êîòî-
ðûé ñëóæèò ìåðîé êà÷åñòâà ýòîãî ýëåìåíòà (â îáùåì ñëó÷àå îïðåäåëÿþ-
ùèé ïàðàìåòð ìîæåò áûòü âåêòîðíûì, ò.å. èìåòü íåñêîëüêî ñîñòàâëÿþ-
ùèõ). Ïàðàìåòð Õ ïîä äåéñòâèåì ñëó÷àéíûõ è äåòåðìèíèðîâàííûõ ôàêòî-
ðîâ (ïðîöåññîâ èçíîñà, ñòàðåíèÿ, ðàçðåãóëèðîâàíèÿ è ò.ä.) èçìåíÿåòñÿ â
ïðîöåññå ýêñïëóàòàöèè (èëè õðàíåíèÿ) ýëåìåíòà è â êîíöå êîíöîâ äîñòè-
ãàåò ïðåäåëüíîãî (êðèòè÷åñêîãî) çíà÷åíèÿ, ïîñëå ÷åãî ñîñòîÿíèå ýëåìåíòà
ñ÷èòàåòñÿ íåðàáîòîñïîñîáíûì, ò.å. ïðîèñõîäèò îòêàç. Îáëàñòü èçìåíåíèÿ
ïàðàìåòðà, â ïðåäåëàõ êîòîðîé ñîñòîÿíèå ýëåìåíòà ñ÷èòàåòñÿ ðàáîòîñïî-
ñîáíûì, íàçûâàåòñÿ ðàáî÷åé îáëàñòüþ èëè ïîëåì äîïóñêà.
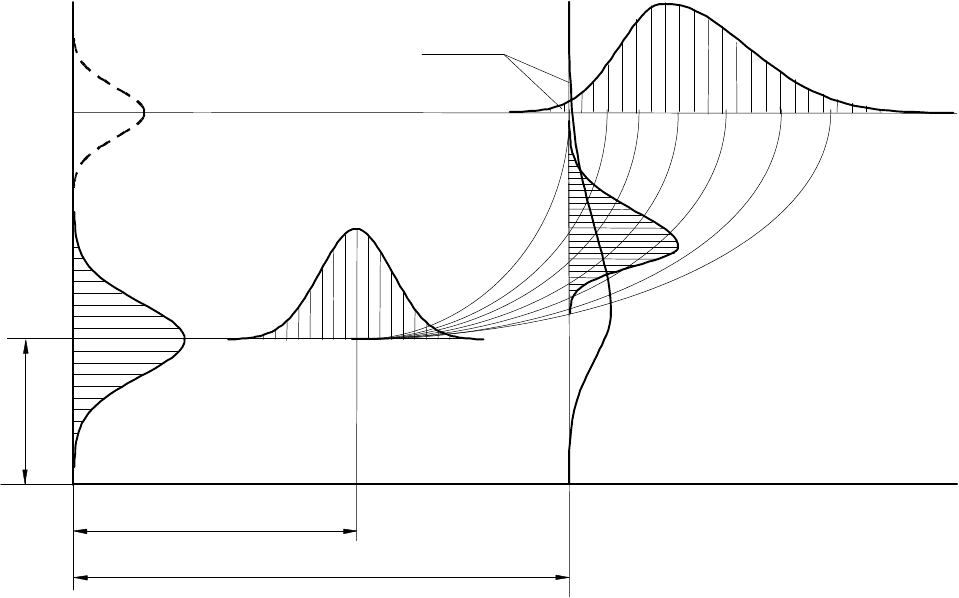
Íà ðèñ.4.7 ïîêàçàíà îáùàÿ ñõåìà âîçíèêíîâåíèÿ ïàðàìåòðè÷åñêîãî îòêàçà, ïðè êî-
òîðîì â ðåçóëüòàòå êàêèõ-ëèáî ïðîöåññîâ (ïîâðåæäåíèÿ, èçíîñà, ñòàðåíèÿ, ðàçðåãóëè-
ðîâàíèÿ è ò.ä.) ïðîèñõîäèò ïîñòåïåííîå èçìåíåíèå îïðåäåëÿþùåãî ïàðàìåòðà Õ. Îòêàç
âîçíèêíåò ïðè äîñòèæåíèè ÷åðåç íåêîòîðûé (â îáùåì ñëó÷àå ñëó÷àéíûé) ïðîìåæóòîê
âðåìåíè ïðåäåëüíî äîïóñòèìîãî ìàêñèìàëüíîãî èëè ìèíèìàëüíîãî çíà÷åíèÿ X
ïð
(äëÿ
îïðåäåëåííîñòè áóäåì ñ÷èòàòü, ÷òî ïàðàìåòð X îãðàíè÷åí ïî çíà÷åíèþ ñâåðõó (X £
X
ïð
= X
max
), õîòÿ îãðàíè÷åíèå ìîæåò áûòü è ñíèçó (X³X
min
, è ñ äâóõ ñòîðîí
(X
min
£X£X
max
)).
Íà ñõåìå ïîêàçàíû îñíîâíûå ýòàïû ôîðìèðîâàíèÿ çàêîíà ðàñïðåäåëåíèÿ âðåìåíè
áåçîòêàçíîé ðàáîòû ýëåìåíòà f(t).  íà÷àëå ýêñïëóàòàöèè èìååò ìåñòî ðàññåèâàíèå íà-
÷àëüíîãî çíà÷åíèÿ îïðåäåëÿþùåãî ïàðàìåòðà f(X
0
) îòíîñèòåëüíî ñâîåãî ìàòåìàòè÷åñêî-
ãî îæèäàíèÿ X
o
, êîòîðîå ìîæåò áûòü ñâÿçàíî ñ íåñòàáèëüíîñòüþ ñâîéñòâ ìàòåðèàëîâ è
òåõíîëîãèè èçãîòîâëåíèÿ ýëåìåíòà, äðóãèìè âíóòðåííèìè è âíåøíèìè ïðè÷èíàìè. Çà-
òåì â ïðîöåññå ýêñïëóàòàöèè ýëåìåíòà îïðåäåëÿþùèé ïàðàìåòð ïîä äåéñòâèåì ïðîèñ-
õîäÿùèõ â íåì ïðîöåññîâ íà÷èíàåò óõóäøàòüñÿ.  îáùåì ñëó÷àå èçìåíåíèå ïàðàìåòðà
t
0
T
X
0
X
ïð
f
(
X
0
)
f
(
t
0
)
f
(
X,t
)
f
(
g
)
f
(
t
)
X
t
1
-P
(
t
)
Ðèñ.4.7. Îáùàÿ ñõåìà ôîðìèðîâàíèÿ ïàðàìåòðè÷åñêîãî îòêàçà [15,25]
150
ìîæåò íà÷àòüñÿ ÷åðåç íåêîòîðûé ïðîìåæóòîê âðåìåíè îò íà÷àëà ýêñïëóàòàöèè t
0
, êî-
òîðûé òàêæå ÿâëÿåòñÿ ñëó÷àéíîé âåëè÷èíîé ñ ðàñïðåäåëåíèåì f(t
0
) îòíîñèòåëüíî ñâî-
åãî ìàòåìàòè÷åñêîãî îæèäàíèÿ, ñâÿçàííûé, íàïðèìåð, ñ ïðîöåññàìè íàêîïëåíèÿ ïîâðå-
æäåíèé. Ñêîðîñòü èçìåíåíèÿ îïðåäåëÿþùåãî ïàðàìåòðà g = dX/dt ïîñëå ïåðèîäà t
0
çàâèñèò îò ïðèðîäû ïðîöåññîâ èçíîñà, ñòàðåíèÿ èëè ðàçðåãóëèðîâàíèÿ è ìíîãèõ äðóãèõ
ïàðàìåòðîâ è â îáùåì ñëó÷àå òàêæå ÿâëÿåòñÿ ñëó÷àéíîé âåëè÷èíîé.  ðåçóëüòàòå âñåõ
ýòèõ ïðîöåññîâ è ÿâëåíèé ïðîèñõîäèò ôîðìèðîâàíèå çàêîíà ðàñïðåäåëåíèÿ f(X,t), îï-
ðåäåëÿþùåãî âåðîÿòíîñòü âûõîäà ïàðàìåòðà X çà ãðàíèöó ïîëÿ äîïóñêà X
ïð
, ò.å. âåðî-
ÿòíîñòü îòêàçà Q(t) = 1 – P(t).
Ðàññìîòðåííàÿ ñõåìà îïèñûâàåò ïðîöåññ âîçíèêíîâåíèÿ ïàðàìåòðè÷åñêèõ îòêàçîâ â
îáùåì âèäå è â êîíêðåòíûõ ñëó÷àÿõ ïðè ÷àñòíûõ çíà÷åíèÿõ õàðàêòåðèñòèê è ïàðàìåò-
ðîâ äîëæíà îòðàæàòü êîíñòðóêòèâíûå îñîáåííîñòè è óñëîâèÿ ýêñïëóàòàöèè êîíêðåòíûõ
ýëåìåíòîâ òåõíè÷åñêèõ ñèñòåì. Íàïðèìåð, äëÿ òèïè÷íîãî ïîñòåïåííîãî ïàðàìåòðè÷å-
ñêîãî îòêàçà õàðàêòåðíî íà÷àëî èçìåíåíèÿ îïðåäåëÿþùåãî ïàðàìåòðà Õ ñðàçó ñ ìîìåí-
òà íà÷àëà ýêñïëóàòàöèè (t
0
= 0). Åñëè ïðè äîñòèæåíèè çíà÷åíèÿ X
ïð
íàáëþäàåòñÿ ðåç-
êîå èçìåíåíèå îïðåäåëÿþùåãî ïàðàìåòðà X(t), òî òàêîé îòêàç áëèçîê ê îòêàçó ôóíê-
öèîíèðîâàíèÿ. Åñëè æå äëÿ âîçíèêíîâåíèÿ îòêàçà îñíîâíóþ ðîëü èãðàåò çàðîæäåíèå
ïðîöåññà (ò.å. ôóíêöèÿ ðàñïðåäåëåíèÿ f(t
0
)), à çàòåì ïðîöåññ ïðîòåêàåò ñ áîëüøîé èí-
òåíñèâíîñòüþ, òî òàêàÿ ìîäåëü áëèçêà ê ìîäåëè âíåçàïíîãî îòêàçà.
Ðàçáðîñ íà÷àëüíîãî çíà÷åíèÿ îïðåäåëÿþùåãî ïàðàìåòðà f(X
0
) ñëåäóåò ó÷èòûâàòü
ïðè ðàñ÷åòàõ íàäåæíîñòè íåêîòîðîé ñîâîêóïíîñòè ýëåìåíòîâ (íàïðèìåð, ïàðòèè äåòà-
ëåé). Äëÿ îäíîãî æå êîíêðåòíîãî ýëåìåíòà çíà÷åíèå X
0
ÿâëÿåòñÿ êîíêðåòíîé íåñëó÷àé-
íîé âåëè÷èíîé. Åñëè æå ðàññìàòðèâàåòñÿ ïîâåäåíèå ýëåìåíòà â ðàçëè÷íûõ ñëó÷àéíûõ
ðåæèìàõ ðàáîòû ïîä âîçäåéñòâèåì ñëó÷àéíûõ âíåøíèõ ôàêòîðîâ, òî è â ñëó÷àå îäíîãî
ýëåìåíòà ïàðàìåòð X
0
ñëåäóåò ðàññìàòðèâàòü êàê ñëó÷àéíóþ âåëè÷èíó.
Ñêîðîñòü èçìåíåíèÿ îïðåäåëÿþùåãî ïàðàìåòðà g = dX/dt ìîæåò áûòü
îïðåäåëåíà ýêñïåðèìåíòàëüíî èëè íà îñíîâàíèè àíàëèçà ìîäåëåé ôèçèêî-
õèìè÷åñêèõ ïðîöåññîâ, ïðîèñõîäÿùèõ â ýëåìåíòå ïðè ýêñïëóàòàöèè.
Ïðîöåññ èçìåíåíèÿ îïðåäåëÿþùåãî ïàðàìåòðà ýëåìåíòà ìîæíî, êàê
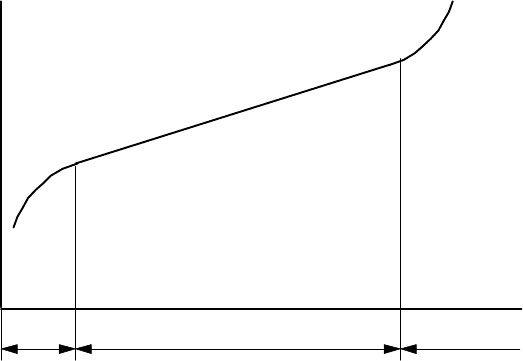
ïðàâèëî, ðàçäåëèòü íà òðè ïåðèîäà (ðèñ.4.8) [9]. Â ïåðâîì ïåðèîäå ïðîèñ-
õîäèò ïðèðàáîòêà ýëåìåíòà, ïîä äåéñòâèåì âíåøíèõ âîçäåéñòâèé è âíóò-
ðåííèõ ïðîöåññîâ ïðîèñõîäèò åãî ïðèñïîñîáëåíèå ê êîíêðåòíûì óñëîâèÿì
ýêñïëóàòàöèè, è ñêîðîñòü èçìåíåíèÿ ïàðàìåòðîâ îáû÷íî äîâîëüíî âåëèêà.
Ê êîíöó ïåðèîäà ïðèðàáîòêè ñêîðîñòü, êàê ïðèâèëî, óìåíüøàåòñÿ è íà
ïðîòÿæåíèè äîñòàòî÷íî ïðîäîëæèòåëüíîãî âòîðîãî (îñíîâíîãî) ïåðèîäà
îñòàåòñÿ ïðèìåðíî ïîñòîÿííîé. Â ïðîöåññå ýêñïëóàòàöèè â ýëåìåíòå ïðî-
èñõîäÿò ðàçëè÷íûå íåîáðàòèìûå ïðîöåññû è íàñòóïàåò ïîñëåäíèé, òðåòèé,
ïåðèîä (èçíîñà è ñòàðåíèÿ), â òå÷åíèå êîòîðîãî ñêîðîñòü èçìåíåíèÿ ïàðà-
ìåòðà X ñòðåìèòåëüíî ðàñòåò è â êîíöå ïåðèîäà ïðîèñõîäèò îòêàç èëè
ýëåìåíò ñíèìàåòñÿ ñ ýêñïëóà-
òàöèè.
Ïåðèîä ïðèðàáîòêè îáû÷-
íî ñîñòàâëÿåò íåñêîëüêî ïðî-
öåíòîâ îò îáùåãî âðåìåíè
ýêñïëóàòàöèè. Êðîìå òîãî,
èíîãäà ïðèðàáîòêà îñóùåñòâ-
ëÿåòñÿ íà çàâîäå-
èçãîòîâèòåëå. Ñ äðóãîé ñòî-
ðîíû, îáû÷íî ýëåìåíòû ïðî-
åêòèðóþòñÿ è èçãîòàâëèâàþò-
ñÿ ñ ðàñ÷åòîì òîëüêî íà âòî-
ðîé (îñíîâíîé) ïåðèîä, è èõ
ýêñïëóàòàöèÿ â òðåòüåì ïå-
1 2 3
t
X
Ðèñ.4.8. Èçìåíåíèå ïàðàìåòðà ýëåìåíòà
â ïðîöåññå ýêñïëóàòàöèè
