Nakahara M. Geometry, Topology and Physics
Подождите немного. Документ загружается.


In (14.18b), 2n∂
z
σ acts like a gauge potential . We also define covariant
derivatives with respect to ¯z,
∇
¯z
(n)
= g
¯zz
∇
(n)
z
, ∇
(n)
¯z
= g
¯zz
∇
z
(n)
. (14.19)
The curvature two-form of K and the scalar curvature associated with the
Christoffel symbols are
= R
z
zz¯z
dz ∧ d¯z =−∂
¯z
(2∂
z
σ)dz ∧ d¯z
=−2∂
z
∂
¯z
σ dz ∧ d¯z (14.20a)
= g
¯zz
Ric
¯zz
+ g
z ¯z
Ric
z ¯z
=−8e
−2σ
∂
z
∂
¯z
σ. (14.20b)
Exercise 14.1. Verify that
∇
z
(n)
= 2e
−2σ
∂
¯z
∇
(n)
z
= e
−2nσ
∂
z
e
2nσ
(14.21a)
∇
¯z
(n)
= 2e
−2(n+1)σ
∂
z
e
2nσ
∇
(n)
¯z
= ∂
¯z
. (14.21b)
∇
z
(n)
and ∇
(n)
z
are mutual adjoints with respect to a properly defined inner
product. Let T , U ∈
n
. We require that the inner product be invariant under a
holomorphic change of the coordinate z → w.Since
g
z ¯z
→|dw/dz|
−2
g
z ¯z
d
2
z
√
g → d
2
w
√
g
¯
T → (
dw/dz)
n
¯
TU→ (dw/dz)
n
U.
We find the combination
(T , U) ≡
d
2
z
√
g(g
z ¯z
)
n
¯
TU (14.22)
is invariant under holomorphic coordinate transformations. Take T ∈
n
and
U ∈
n+1
.Wefindthat
(U, ∇
z
(n)
T ) =
d
2
z e
2σ
2
−n−1
e
2(n+1)σ
¯
U 2e
−2σ
∂
¯z
T
=−2
−n
d
2
zT∂
¯z
[e
(2n+1)σ
¯
U] (partial integration)
=−2
−n
d
2
zTe
(2n+1)σ
[∂
z
U + (2n + 1)(∂
z
σ)U]
=−
d
2
z
√
g(g
z ¯z
)
n
[∇
(n+1)
z
U]
¯
T = (−∇
(n+1)
z
U, T ).
This shows that
(∇
z
(n)
)
†
=−∇
(n+1)
z
. (14.23a)

Exercise 14.2. Show that
(∇
(n)
z
)
†
=−∇
z
(n−1)
.(14.23b)
We define two kinds of Laplacian
±
(n)
:
n
→
n±1
→
n
by
+
(n)
≡−∇
(n+1)
z
∇
z
(n)
=−2e
−2σ
[∂
z
∂
¯z
+ 2n(∂
z
σ)∂
¯z
] (14.24a)
−
(n)
≡−∇
z
(n−1)
∇
(n)
z
=−2e
−2σ
[∂
z
∂
¯z
+ 2n(∂
z
σ)∂
¯z
+ 2n(∂
z
∂
¯z
σ)]. (14.24b)
Then it follows that
+
(n)
−
−
(n)
= 4ne
−2σ
(∂
z
∂
¯z
σ) =−
1
2
n . (14.25)
This shows, in particular, that
+
(0)
=
−
(0)
(≡
(0)
). (14.26)
14.1.4 The Riemann–Roch theorem
Here we derive a version of the Riemann–Roch theorem from the Atiyah–Singer
index theorem following D’Hoker and Phong (1988).
Theorem 14.1. (Riemann–Roch theorem)Let
g
be a Riemann surface of genus
g. Then the index of the operator ∇
(n)
z
is
dim
ker ∇
(n)
z
− dim ker ∇
z
(n−1)
= (2n − 1)(g − 1). (14.27)
Proof. We use the heat kernel to evaluate the index. We first note that ker ∇
(n)
z
=
ker
−
(n)
and ker ∇
z
(n−1)
= ker
+
(n−1)
(see (14.24)). The heat kernel
+
n
of
+
(n)
satisfies
∂
∂t
+
+
(n)
+
n
(z,w;t) =
∂
∂t
+ − V
n
+
n
(z,w;t) = 0
where ≡−2∂
z
∂
¯z
is the flat-space Laplacian and
V
n
≡ −
+
(n)
= (1 −e
−2σ
) + 4ne
−2σ
∂
z
σ∂
¯z
.
The Laplacian also defines a heat kernel by
∂
∂t
+
K (z,w;t) = 0
which is easily solved to yield
K (z,w;t) =
1
4πt
e
−|z−w|
2
/2t
.

The perturbative computation and iteration yield
+
n
(z, z
;t) = K (z, z
;t)
+
t
0
ds
dw K (z,w;t − s)V
n
(w)
+
n
(w, z
;s)
= K (z, z
;t) +
ds
dw K (z,w;t − s)V
n
(w)K (w, z
;s)
+
ds
ds
dv
dw K (z,v;t − s)V
n
(v)
× K (v, w;s − s
)V
n
(w)K (w, z
;s
)
+···.
We are particularly interested in
+
n
(z, z;t), t being small,
+
n
(z, z;t) =
1
4πt
+
t
0
ds
dw K (z,w;t − s)V
n
(w)K (w, z;s) + (t).
(14.28)
If we take a coordinate system in which σ = 0atz,wehave
σ(w) 0 + ∂
z
σ(w − z) + ∂
¯z
σ( ¯w −¯z)
+
1
2
[∂
2
z
σ(w − z)
2
+ ∂
2
¯z
σ( ¯w −¯z)
2
+ 2∂
z
∂
¯z
σ |w − z|
2
]+···.
Due to rotational symmetry in two-dimensional space, only those terms with
one z-derivative and one ¯z-derivative survive in the integral in (14.28). Terms
proportional to ∂
z
σ∂
¯z
σ cancel between the second and third terms in the
expansion and we are left with terms proportional to ∂
z
∂
¯z
σ .Nowwehaveto
evaluate
t
0
ds
d
2
w K (z,w;t − s)
×[2∂
z
∂
¯z
σ |¯w −¯z|
2
w
+ 4n( ¯w −¯z)∂
z
∂
¯z
σ∂
¯w
]K (w, z;s).
From the identities
d
2
w K (z,w;t − s)|w − z|
2
w
K (w, z;s)
=
1
16π
2
s
2
(t − s)
d
2
w|w|
2
exp
−
t
2s(t − s)
|w|
2
−
1
32π
2
s
3
(t − s)
d
2
w|w|
4
exp
−
t
2s(t − s)
|w|
2
=
(t − s)(2s − t)
2πt
3
and
d
2
w K (z,w;t − s)(¯z −¯w)∂
¯w
K (w, z;s)
=
1
32π
2
s
2
(t − s)
d
2
w exp
−
t
2s(t − s)
|w|
2
=
t − s
4πt
2
we find that
+
n
(z, z;t) =
1
4πt
+
1 +3n
12π
σ +
(t). (14.29a)
We also have the diagonal part of the heat kernel
−
n
for
−
(n)
,
−
n
(z, z;t) =
1
4πt
+
1 −3n
12π
σ +
(t). (14.29b)
From (14.29) and (14.20b), we obtain
ind ∇
(n)
z
=
d
2
z
1 −3n
12π
−
1 +3(n − 1)
12π
σ =
1 −2n
8π
d
2
x
=−
2n − 1
2
χ(
g
) = (2n − 1)(g − 1)
where
χ =
1
4π
d
2
x = 2 − 2g
is the Euler characteristic of
g
.
14.2 Quantum theory of bosonic strings
Now we are ready to introduce Polyakov’s formulation of bosonic strings, which
is based on the path integral over geometries. Since the string action contains an
enormous symmetry, we have to pay special attention to counting independent
geometries once and only once. This is achieved by the Faddeev–Popov trick.
Our argument will be restricted to the simplest case, namely closed orientable
bosonic strings; the theory is defined on Riemann surfaces.
14.2.1 Vacuum amplitude of Polyakov strings
According to the general prescription of the path integral formalism, the partition
function (vacuum-to-vacuum amplitude) of the string theory is given by
Z =
∞
g=0
Z
g
=
∞
g=0
X γ e
−S[X,γ ]
(14.30)
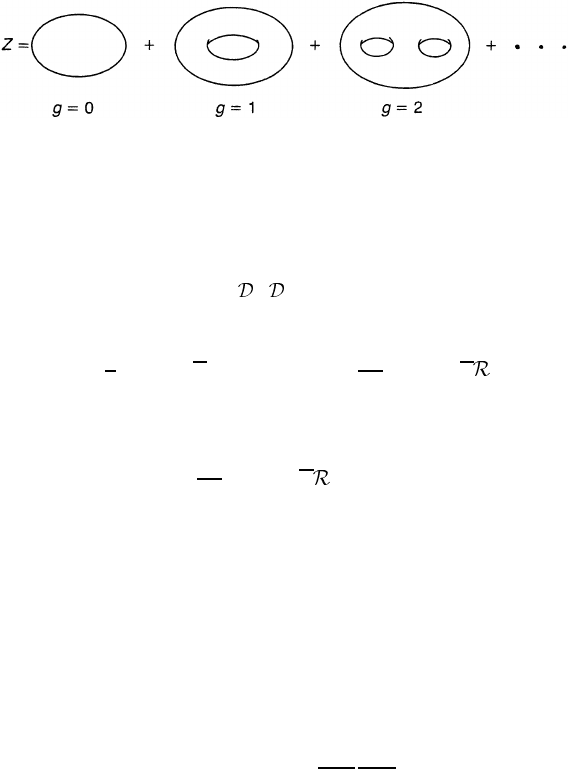
Figure 14.1. The total vacuum amplitude is given by summing over g-loop amplitudes.
see figure 14.1. To avoid confusion, we denote the genus by g and the metric by
γ . The sum over genera amounts to the sum over the topologies. Z
g
is the g-loop
amplitude and is obtained by integrating over all metrics γ and all embeddings X.
As we shall see later, the measure
X γ is not well defined and we need some
modifications. The string action S[X,γ] is taken to be
S[X,γ]≡
1
2
d
2
ξ
√
γγ
αβ
∂
α
X
µ
∂
β
X
µ
+
λ
4π
d
2
ξ
√
γ . (14.31)
The first term is the Polyakov action. The second term is proportional to the Euler
characteristic
χ =
1
4π
d
2
ξ
√
γ = 2 − 2g
and serves as the string coupling constant; the amplitude of a loop with genus g is
suppressed by the factor e
−2λg
. Since this term is a topological invariant, it does
not affect the dynamics of the string. We are interested in Riemann surfaces of a
fixed genus g and drop this term. The first term of the action has the following
symmetries (section 7.11):
(A) Diff(
g
), the group of diffeomorphisms f :
g
→
g
.Letξ
α
→ ξ
α
(ξ) be
the coordinate expression for f . The new metric is the pullback of the old
one whose coordinate component expression is
γ
αβ
→ f
∗
γ
αβ
=
∂ξ
γ
∂ξ
α
∂ξ
δ
∂ξ
β
γ
γδ
. (14.32)
The embedding also gets transformed as
X
µ
→ f
∗
X
µ
= X
µ
f. (14.33)
The invariance of the classical action takes the form
S[X,γ]=S[ f
∗
X, f
∗
γ ]. (14.34)
(B) Weyl(
g
), the group of two-dimensional Weyl rescalings
γ
αβ
→ˆγ
αβ
≡ e
φ
γ
αβ
(14.35)

Figure 14.2. An element of ×
g
is obtained by the action of Diff(
g
) ∗Weyl(
g
) on
an element (X,γ) in the gauge slice.
where φ ∈ (
g
). The conformal invariance of S takes the form
S[X,γ]=S[X, ˆγ ]. (14.36)
The symmetries (A) and (B) must be preserved under quantization, otherwise
the theory has anomalies.
According to the standard Faddeev–Popov formalism, the degrees of
freedom corresponding to these symmetries have to be omitted when we define
Z
g
. For example, the string geometry specified by the pairs (X
1
,γ
1
) and
(X
2
,γ
2
) should not be counted independently if they are related by an element of
Diff(
g
). Similarly, (X,γ) and (X, e
φ
γ) should not be counted as independent
configurations. Unless special attention is paid, we would count the same
configurations infinitely many times, which leads to disastrous divergences. It
turns out that the space of all the geometries (X,γ) can be separated into
equivalence classes (the gauge slice), any two points of which cannot be
connected by these symmetries, see figure 14.2.
To be more mathematical, let
be the space of all the embeddings X :
g
→
D
and let
g
be the space of all the metrics defined on
g
.Naively,
the path integral is defined over
×
g
. Because of the symmetries (A) and
(B), however, the integral should be restricted to the quotient space (
×
g
)/G
where G = Diff(
g
) ∗ Weyl(
g
) is the gauge group.
3
The action of ( f, e
φ
) on
(X,γ) ∈
×
g
is
( f, e
φ
)(X,γ)= ( f
∗
X, e
φ
f
∗
γ). (14.37)
The quotient
g
/G is called the moduli space of
g
and is denoted by
Mod(
g
). We are also interested in the subgroup Diff
0
(
g
) of Diff(
g
),which
3
Here ∗ denotes the semi-direct product. Note that Diff(
g
) ∩ Weyl(
g
) =∅. We shall come back
to this point later.
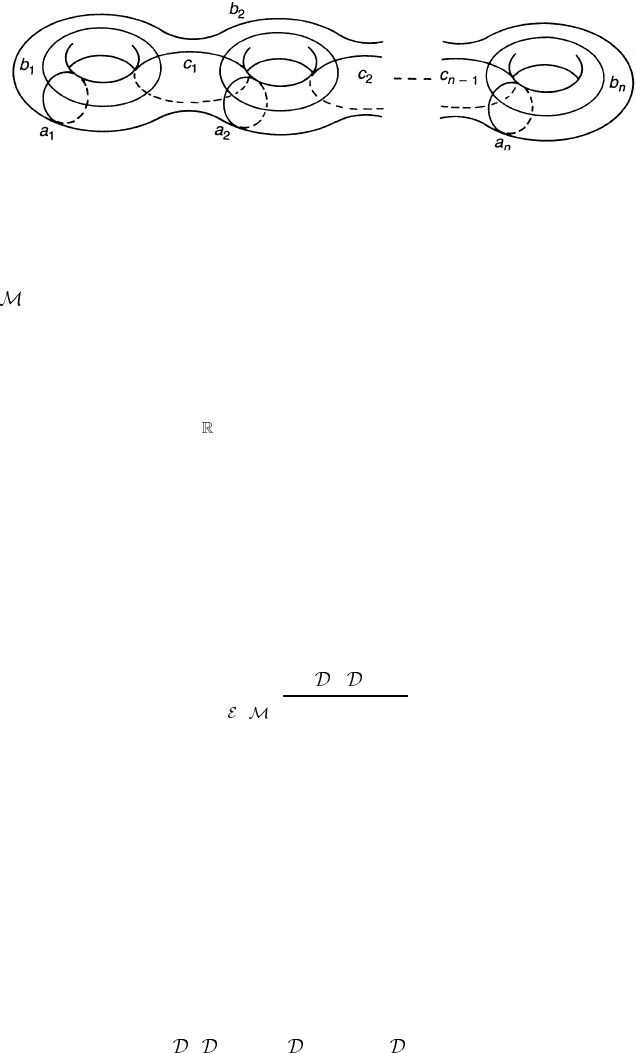
Figure 14.3. The mapping class group (MCG) is generated by Dehn twists around a
i
, b
i
and c
i
(1 ≤ i ≤ g).
is a connected component of the identity map. The quotient space Teich(
g
) ≡
g
/Diff
0
(
g
) ∗ Wey l (
g
) is called the Te i ch m ¨uller space of
g
. The general
theory of Riemann surfaces shows that Teich(
g
) is a finite-dimensional universal
covering space of Mod(
g
). Explicitly, we have
dim
Teich(
g
) =
0 g = 0
2 g = 1
6g − 6 g ≥ 2.
(14.38)
The group Diff(
g
)/Diff
0
(
g
) is known as the modular group (MG) or the
mapping class group (MCG). The MCG is generated by the Dehn twists defined
in example 8.2. For the torus with genus g, the MCG is generated by 3g −1Dehn
twists around a
i
, b
i
and c
i
in figure 14.3. Unfortunately, these 3g −1Dehntwists
are not the minimal set of the generators. The general form of MCG for g ≥ 2is
not well understood.
From these arguments, the meaningful partition function turns out to be
Z
g
≡
×
g
X γ
V (Diff ∗ Wey l)
e
−S[X,γ ]
(14.39)
where V (Diff ∗ Weyl) is the (infinite) volume of the space of Diff(
g
)∗Weyl(
g
)
and takes care of the infinite overcounting of the same geometry. The order (the
number of elements) of MCG is denoted by |MCG|. Clearly,
V (Diff ∗ Wey l) =|MCG|V (Diff
0
∗ Weyl). (14.40)
14.2.2 Measures of integration
We have to define a sensible measure to carry out the integration (14.39) so that
the physical degrees of freedom and the gauge degrees of freedom are separated.
This separation of degrees of freedom requires the Jacobian,
γ X → J ( physical)( gauge). (14.41)

To find this Jacobian, we note that the Jacobian on a manifold M agrees with that
on TM. To see this, let x
µ
(y
µ
) be a coordinate of a chart U (V ) of M such that
U ∩ V =∅. The Jacobian of the coordinate change is J = det(∂y
µ
/∂x
ν
).Take
V ∈ T
p
M. In components, we have V = u
µ
∂/∂x
µ
= v
µ
∂/∂y
µ
,where
v
µ
= u
ν
(∂y
µ
/∂x
ν
). (14.42)
{u
µ
} and {v
µ
} are fibre coordinates of T
p
M. The Jacobian
ˆ
J associated with this
coordinate change is
ˆ
J = det(∂v
µ
/∂u
ν
) = det(∂y
µ
/∂x
ν
) = J. (14.43)
This shows that the Jacobian at p ∈ M is the same as that on T
p
M. The Jacobian
ˆ
J depends on p but not on the vector itself, since J depends only on p.
Example 14.2. Let (x, y) and (r,θ)be coordinates of
2
,wherex = r cos θ and
y = r sin θ . The Jacobian of the coordinate change is
J = det
∂(x, y)
∂(r,θ)
= r.
Let us take
V = v
x
∂/∂x + v
y
∂/∂y = v
r
∂/∂r + v
θ
∂/∂θ ∈ T
p
R
2
.
(v
x
,v
y
) and (v
r
,v
θ
) serve as fibre coordinates of T
p
2
.Since
v
x
= v
r
∂x /∂r + v
θ
∂x /∂θ v
y
= v
r
∂y/∂r + v
θ
∂y/∂θ
the associated Jacobian
ˆ
J is easily calculated to be
ˆ
J = det[∂(v
x
,v
y
)/∂(v
r
,v
θ
)]=
∂x /∂r ∂ x/∂θ
∂y/∂r ∂y/∂θ
= J.
Let us derive this Jacobian in an indirect but suggestive way. We normalize
themeasured
2
v as
4
1 =
d
2
v exp(−
1
2
v
2
) =
dv
x
dv
y
exp[−
1
2
(v
2
x
+ v
2
y
)].
We also have v
2
2
= v
2
r
+ r
2
v
2
θ
. Noting that the Jacobian is independent of v
r
and v
θ
,wehave
1 = J
dv
r
dv
θ
exp[−
1
2
(v
2
r
+r
2
v
2
θ
)]=Jr
−1
4
This normalization of the measure differs by a constant factor from the conventional one.
from which we find J = r . We use this procedure to find the functional measure
of string theory.
5
This analysis enables us to write
δγ δ X = J δ(physical) δ(gauge) (14.44)
where δγ (δX) is a small variation of the metric γ (the embedding X)andis
regarded as an element of T
γ
(
g
)(T
X
). The meaning of the RHS becomes
clear in a moment.
Consider the diffeomorphism generated by an infinitesimal vector field δv
on
g
.Sinceδv is infinitesimal, it belongs to Diff
0
(
g
) rather than the full group
Diff(
g
). The changes of the metric and the embedding under δv are (see (7.120))
δ
D
γ
αβ
= (
δv
γ)
αβ
=∇
α
δv
β
+∇
β
δv
α
δ
D
X = δv
α
∂
α
X. (14.45)
The changes of γ and X under an infinitesimal Weyl rescaling e
δφ
are
δ
W
γ
αβ
= δφγ
αβ
δ
W
X = 0. (14.46)
These changes belong to unphysical (gauge) degrees of freedom. In general, a
small change of metric is given by
δγ
αβ
= δ
W
γ
αβ
+ δ
D
γ
αβ
+ (physical change)
= δφγ
αβ
+∇
α
δv
β
+∇
β
δv
α
+ δt
i
∂
∂t
i
γ
αβ
(t) (14.47)
where the last term is called the Te ic hm ¨uller deformation of the metric, which
can neither be described by a diffeomorphism nor by a Weyl rescaling. As
mentioned before, {i } is a finite set, 1 ≤ i ≤ n = dim
Teich(
g
).Itis
convenient for later purposes to separate δγ into a traceless part and a part with a
non-zero trace. We write
δγ
αβ
= δ
¯
φγ
αβ
+ (P
1
δv)
αβ
+ δt
i
T
iαβ
(t) (14.48)
where T
iαβ
is the traceless part of the Teichm¨uller deformation,
T
iαβ
≡
∂γ
αβ
∂t
i
−
1
2
γ
αβ
γ
γδ
∂γ
γδ
∂t
i
. (14.49)
The operator P
1
is defined by
(P
1
δv)
αβ
≡∇
α
δv
β
+∇
β
δv
α
− γ
αβ
(∇
γ
δv
γ
) (14.50)
and picks up the traceless part of δ
D
γ
αβ
while δ
¯
φ is defined by
δ
¯
φ = δφ +
∇
γ
δv
γ
+ trace part of δt
∂γ
∂t
(14.51)
5
It should be kept in mind that we introduce the tangent space only to obtain the Jacobian. The
tangent space itself has no physical relevance.

where we do not need the explicit form in the parentheses.
As for the embeddings, we consider the quotient
/Diff(
g
). An arbitrary
embedding X is obtained by the action of Diff(
g
) on some
˜
X ∈ /Diff(
g
).
Then a small change of the embedding is expressed as
δ X = δv
α
∂
α
˜
X + δ
˜
X (14.52)
where the first term represents the change of X generated by δv while the second
is not associated with diffeomorphisms. Now the measure should look like
δγ δ X = J d
n
t δv δφ δ
˜
X . (14.53)
To define the measure, we need to specify a metric on the tangent space, see
example 14.2. We restrict ourselves to the so called ultralocal metric which is
quadratic and depends on γ
αβ
but not on ∂γ
αβ
. Define a metric for symmetric
second-rank tensors by
δh
2
γ
=
d
2
ξ
√
γ(G
αβγ δ
+ uγ
αβ
γ
γδ
)δh
αβ
δh
γδ
(14.54a)
where u > 0 is an arbitrary constant and
G
αβγ δ
≡ γ
αγ
γ
βδ
+ γ
αδ
γ
βγ
− γ
αβ
γ
γδ
. (14.55)
It is readily verified that G is the projection operator to the traceless part
(tr G
αβγ δ
δh
γδ
= γ
αβ
G
αβγ δ
δh
γδ
= 0) while uγ
αβ
γ
γδ
is that to the trace part.
In a finite-dimensional manifold, a metric defines a natural volume element. In
the present case, however, the measure cannot be defined explicitly and we have
to define it implicitly in terms of the Gaussian integral (see example 14.2),
δh exp(−
1
2
||δh||
2
γ
) = 1. (14.56a)
Similarly, the metrics for a scalar δφ, a vector δv and a map δ X
µ
are defined by
δφ
2
γ
=
d
2
ξ
√
γδφ
2
(14.54b)
δv
2
γ
=
d
2
ξ
√
γγ
αβ
δv
α
δv
β
(14.54c)
δX
2
γ
=
d
2
ξ
√
γδX
µ
δ X
µ
. (14.54d)
With these metrics, the measures are defined by
δφ exp(−
1
2
||δφ||
2
γ
) = 1 (14.56b)
δv exp(−
1
2
||δv||
2
γ
) = 1 (14.56c)
δ X exp(−
1
2
||δ X ||
2
γ
) = 1. (14.56d)
