Nakahara M. Geometry, Topology and Physics
Подождите немного. Документ загружается.


The periodic boundary condition forces us to take the set of loops in
M, which we will denote as L(M), as the configuration space of the bosonic
coordinates. To apply the saddle point method to the evaluation of the path
integral, we have to find the set
of the extrema of the action, namely the
solutions of the classical Euler–Lagrange equations
−g
λµ
(x )
D ˙x
µ
Dt
+
1
2
R
µνλρ
ψ
µ
ψ
ν
˙x
ρ
= 0 (12.176)
Dψ
µ
Dt
=
dψ
µ
dt
+˙x
λ
µ
λν
ψ
ν
= 0. (12.177)
It is instructive to outline the derivation of these equations since the anti-
commutativity of Grassmann numbers and the symmetries of the Riemann tensor
are fully utilized. The Euler–Lagrange equation for ψ
µ
is
0 =
∂ L
∂ψ
ρ
−
d
dt
∂ L
∂
˙
ψ
ρ
=
1
2
g
ρν
Dψ
ν
Dt
−
1
2
g
κν
ψ
κ
˙x
λ
ν
λρ
+
1
2
d
dt
g
ρν
ψ
ν
=
1
2
g
ρν
Dψ
ν
Dt
− g
κν
˙x
λ
ν
λρ
ψ
κ
+
∂
λ
g
ρν
˙x
λ
ψ
ν
+ g
ρν
˙
ψ
ν
.
By multiplying both sides by g
µρ
and summing over ρ,wehave
0 =
Dψ
µ
Dt
− g
µρ
g
κν
˙x
λ
ν
λρ
ψ
κ
+ g
µρ
∂
λ
g
ρν
˙x
λ
ψ
ν
+
˙
ψ
µ
=
Dψ
µ
Dt
+
˙
ψ
µ
+˙x
λ
g
µρ
∂
λ
g
ρν
− g
µρ
g
νκ
κ
λρ
ψ
ν
= 2
Dψ
µ
Dt
which proves (12.177). Here, use has been made of the identity
g
µρ
[(∂
λ
g
ρν
) −
1
2
(∂
λ
g
νρ
+ ∂
ρ
g
νλ
− ∂
ν
g
λρ
)]
= g
µρ 1
2
∂
λ
g
ρν
+ ∂
ν
g
λρ
− ∂
ρ
g
νλ
=
µ
νλ
in the square brackets in the second line above.
Let us prove the equation of motion for x
µ
next. We find
∂ L
∂x
µ
−
d
dt
∂ L
∂ ˙x
µ
=
1
2
(∂
µ
g
αβ
) ˙x
α
˙x
β
+
1
2
(∂
µ
g
αβ
)ψ
α
Dψ
β
Dt
+
1
2
g
αβ
ψ
α
˙x
λ
∂
µ
β
λκ
ψ
κ
−
d
dt
g
µν
˙x
ν
+
1
2
g
αβ
ψ
α
β
µκ
ψ
κ
=−[g
µν
¨x
ν
+
1
2
(∂
λ
g
µν
+ ∂
ν
g
µλ
− ∂
µ
g
νλ
) ˙x
ν
˙x
λ
]
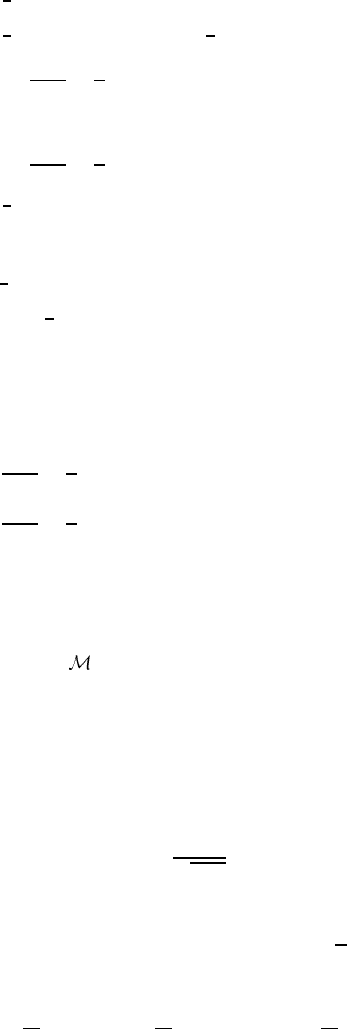
+
1
2
[g
αβ
∂
µ
β
λκ
− ∂
λ
g
αβ
β
µκ
− g
αβ
∂
λ
β
µκ
]ψ
α
ψ
κ
˙x
λ
+
1
2
g
αβ
˙x
λ
α
λγ
ψ
γ
β
µκ
ψ
κ
+
1
2
g
αβ
ψ
α
β
µκ
˙x
λ
κ
λν
ψ
ν
=−g
µν
D ˙x
ν
Dt
+
1
2
[g
αβ
∂
µ
β
λκ
− g
αβ
∂
λ
β
µκ
− ∂
λ
g
αβ
β
µκ
+ g
γβ
γ
λα
β
µκ
+ g
αβ
β
µγ
γ
λκ
]ψ
α
ψ
κ
˙x
λ
=−g
µν
D ˙x
ν
Dt
+
1
2
(∂
µ
β
λκ
− ∂
λ
β
µκ
+
β
µκ
γ
λκ
)ψ
α
ψ
κ
˙x
λ
+
1
2
(g
γβ
γ
λα
− ∂
λ
g
αβ
)
β
µκ
ψ
α
ψ
κ
˙x
λ
.
The last term of the last line of this equation is written as
[g
γβ
1
2
g
γν
(∂
λ
g
να
+ ∂
α
g
νλ
− ∂
ν
g
λα
) − ∂
λ
g
αβ
]
β
µν
ψ
α
ψ
κ
˙x
λ
=−
1
2
(∂
λ
g
αβ
+ ∂
β
g
λα
− ∂
α
g
λβ
)
β
µν
ψ
α
ψ
κ
˙x
λ
=−
αλβ
β
µκ
ψ
α
ψ
κ
˙x
λ
=−g
αβ
β
λβ
β
µκ
ψ
α
ψ
κ
˙x
λ
from which we obtain
0 =−g
µν
D ˙x
ν
Dt
+
1
2
(∂
µ
β
λκ
− ∂
λ
β
µκ
+
β
µγ
γ
λκ
−
β
λγ
γ
µκ
)ψ
α
ψ
κ
˙x
λ
=−g
µν
D ˙x
ν
Dt
+
1
2
R
ακµλ
ψ
α
ψ
κ
˙x
λ
.
Equation (12.176) follows by renaming dummy indices.
Let us come back to the study of the solutions of the equations of motion
(12.176) and (12.177). Clearly, the pair x = constant and ψ = constant is one of
solutions. Therefore, x
p
: t → p ∈ M is always contained in the solutions, which
may be written as M ⊂
. Equation (12.176) reduces to the geodesic equation
when ψ = 0 but not necessarily so in general. When the fundamental group
π
1
(M) is non-trivial, there exist non-contractible geodesics in general. Their
contributions to the path integral, however, vanish exponentially as exp(−c/β)
as β ↓ 0 and, hence, are negligible.
Before we proceed to the proof of the index theorem, we need to explain the
saddle point method. Let us start with a simple example. Consider the integral
Z =
∞
−∞
dx
√
2π
¯
h
e
− f (x )/
¯
h
.
The function f (x) is assumed to have only one minimum at x = x
0
and that
f (x ) →∞as x →±∞. Let us consider the asymmptotic expansion of the
integral Z when the limit
¯
h → 0 is taken. Put x = x
0
+
√
¯
hy and expand f (x) at
x
0
.Taking f
(x
0
) = 0 into account, we obtain the expansion
f (x ) = f (x
0
) +
1
2!
¯
hy
2
f
(x
0
) +
1
3!
¯
h
3/2
y
3
f
(3)
(x
0
) +
1
4!
¯
h
2
y
4
f
(4)
(x
0
) +···.
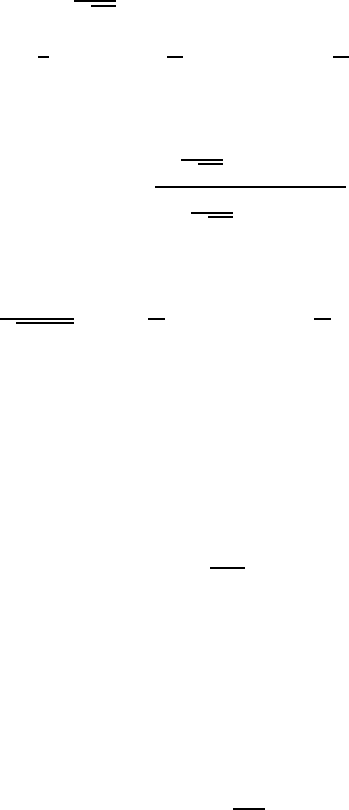
If this expansion is substituted into Z,wehave
Z = e
− f (x
0
)/
¯
h
∞
−∞
dy
√
2π
× exp
−
1
2
y
2
f
(x
0
) −
1
3!
¯
h
1/2
y
3
f
(3)
(x
0
) +
1
4!
¯
hy
4
f
(4)
(x
0
) +···
.
Let us define the moment of y by
y
n
=
dy
√
2π
y
n
e
−y
2
f
(x
0
)/2
dy
√
2π
e
−y
2
f
(x
0
)/2
.
Then we finally obtain the expansion of Z as
Z =
e
− f (x
0
)/
¯
h
f
(x
0
)
2
exp
−
1
3!
¯
h
1/2
y
3
f
(3)
(x
0
) −
1
4!
¯
hy
4
f
(4)
(x
0
) ···
3
.
One might think that one will get terms of order O(
¯
h
1/2
) if ···is expanded.
However, this is not the case since y
3
=0 and one has ··· = 1 + O(
¯
h) in
reality. In the proof of the following index theorem, the parameter
¯
h is replaced
by β. The index is, however, independent of β and we conclude that terms of
order O(β) vanish and, hence, we need to take only the extrema of the action and
the second-order fluctuations thereof into account.
Exercise 12.11. Use the previous expansion to prove the Staring formula
n!
√
2πne
−n
n
n
(12.178)
for n ) 1.
Let us come back to SUSYQM. We take the second-order fluctuation around
the solutions of the classical equations of motion in evaluating Z . The principal
contribution to the path integral comes from the solution x = x
0
and ψ = ψ
0
.We
employ the Riemann normal coordinate based at x = x
0
to make our life easier.
This is to take a coordinate system in which the metric tensor satisfies conditions
7
g
µν
(x
0
) = δ
µν
∂
∂x
λ
g
µν
(x
0
) = 0.
Thus, we have g ≡ det g = 1. We define the fluctuations in this coordinate system
as
x
µ
(t) = x
µ
0
+ ξ
µ
(t)
ψ
µ
(t) = ψ
µ
0
+ η
µ
(t).
7
Of course, this choice does not imply that the Riemann tensor vanishes in general.
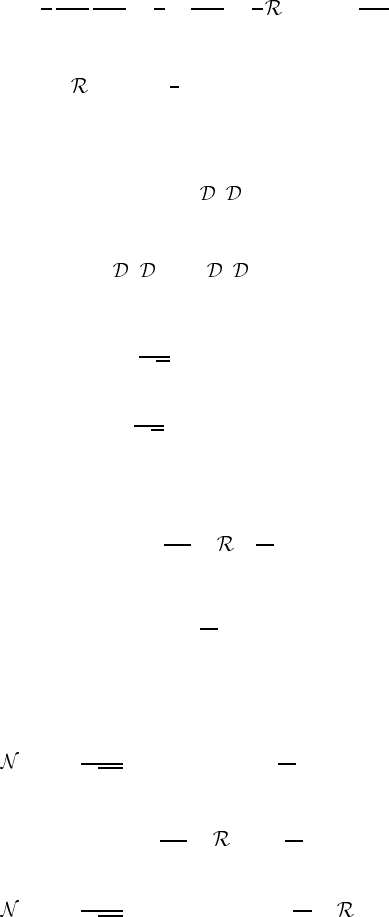
Note here that dx
µ
= dξ
µ
, dψ
µ
= dη
µ
. The second-order expansion of the
action is now written as
S
2
=
β
0
dt
1
2
dξ
µ
dt
dξ
µ
dt
+
1
2
η
µ
dη
µ
dt
+
1
2
˜
µν
(x
0
)ξ
µ
dξ
ν
dt
(12.179)
wherewehaveput
˜
µν
(x
0
) =
1
2
R
µνρσ
(x
0
)ψ
ρ
0
ψ
σ
0
.
Needless to say, the zeroth-order action S
0
= S(x
0
,ψ
0
) vanishes identically.
Let us evaluate the index
ind Q =
ξ ηe
−S
2
(12.180)
using the second-order action S
2
. Here we have taken the translational invariance
of the path integral measure
x ψ = ξ η. Taking the periodic boundary
condition of ξ,η into account, their Fourier expansions are given by
ξ
µ
=
1
√
β
∞
n=−∞
ξ
µ
n
e
2πint/β
η
µ
=
1
√
β
∞
n=−∞
η
µ
n
e
2πint/β
.
The fluctuation operator for ξ in S
2
is
−δ
µν
d
2
dt
2
+
˜
µν
d
dt
while that for η is
δ
µν
d
dt
.
We have to consider the zero modes ξ
µ
0
and η
µ
0
,forwhichn = 0, separately in
the following Gaussian integrals.
8
Taking these into account, we write
ind Q =
d
µ=1
dξ
µ
0
√
2π
dη
µ
0
Det
PBC
δ
µν
d
dt
1/2
×
Det
PBC
−δ
µν
d
2
dt
2
+
˜
µν
(x
0
)
d
dt
−1/2
=
d
µ=1
dξ
µ
0
√
2π
dη
µ
0
Det
PBC
−δ
µν
d
dt
+
˜
µν
(x
0
)
−1/2
(12.181)
8
The integrations over ξ
0
and η
0
are equivalent with those over x
0
and ψ
0
.

where indicates that the zero modes are omitted while is the normalization
factor, which takes care of the ambiguities associated with the ordering of
Grassmann numbers. Let us evaluate this factor now.
Since ind Q is independent of β, we put β = 1 for simplicity. We also
simplify our calculation by choosing the metric to be g
µν
= δ
µν
. Then the
fermion and boson parts separate completely. The fermionic part is evaluated,
by noting H
fermion
= 0, to yield
Tr γ
2n+1
=
PBC
ψe
−
1
2
1
0
ψ·
˙
ψ dt
=
f
Det
PBC
(δ
µν
∂
t
)
1/2
dψ
1
0
···dψ
2n
0
,
where ψ
µ
0
is the zero mode. The determinant is evaluated as follows. First, note
that the argument in section 1.5 shows that the determinant is, in fact,
Det
PBC
(
∂
t
+ ω
)
= lim
ε→0
Det
(
(1 − εω)∂
t
+ ω
)
where we have introduced the harmonic oscillator frequency ω, which will be set
to zero at the end of the calculation. The ‘partition function’ is
tr(−1)
F
e
−β H
= 2sinh(βω/2)
= e
βω/2
Det
PBC
(
(1 −εω)∂
t
+ ω
)
. (12.182)
Therefore, the determinant in the limit ω → 0is
Det
PBC
(
∂
t
)
= lim
ω→0
e
−βω/2
2sinh(βω/2) = 1. (12.183)
Thus, we finally obtained
Tr γ
2n+1
=
f
dψ
1
0
...dψ
2n
0
. (12.184)
We insert
γ
2n+1
= i
n
γ
1
0
...γ
2n
0
= (2i)
n
ψ
1
0
...ψ
2n
0
further in the trace. Since Tr γ
2
2n+1
= Tr I = 2
n
, we obtain
Tr γ
2
2n+1
= 2
n
=
f
dψ
1
0
...dψ
2n
0
(2i)
n
ψ
1
0
...ψ
2n
0
=
f
(−2i)
n
which leads to
f
= i
n
.
Next, we evaluate the normalization factor
b
of the boson part. If we employ
imaginary time in (1.101) to obtain x, 1|x, 0=(2π)
−1/2
,wehave
x
µ
e
−
1
2
1
0
˙x
µ 2
=
b
1
Det
1/2
(−δ
µν
∂
2
t
)
2n
µ=1
dx
µ
√
2π
= (2π)
−n
2n
µ=1
dx
µ
.
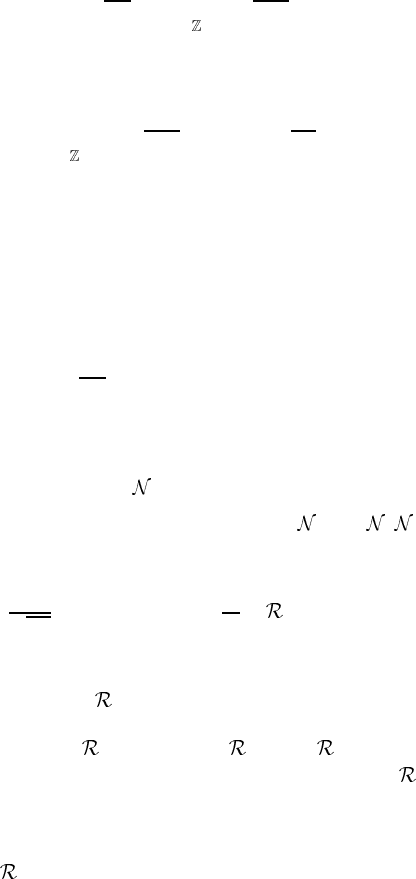
The determinant is evaluated using the ζ -function regularization as in section 1.4.
The eigenvalue of −d
2
/dt
2
with the periodic boundary condition is λ
n
=
(
2nπ/β
)
2
and then
Det
PBC
−
d
2
dt
2
=
n∈ ,n=0
2πn
β
2
.
The spectral ζ -function is
ζ
−d
2
/dt
2
(s) =
∞
n∈ ,n=0
2nπ
β
2
−s
= 2
β
2π
2s
ζ(2s)
from which we find
ζ
−d
2
/dt
2
(0) = 4log(β/2π)e
2s log(β/2π)
ζ(2s) + 4e
2s log(β/2π)
ζ
(2s)|
s=0
= 4[log(β/2π)ζ(0) + ζ
(0)]=−2logβ.
Therefore, the determinant is
Det
PBC
−
d
2
dt
2
= exp[−ζ
−d
2
/dt
2
(0)]=β
2
. (12.185)
By putting β = 1, we find Det
PBC
−d
2
/dt
2
= 1. Thus, we have obtained the
normalization factor
b
= 1.
Putting these results together, we have shown that
=
f b
= i
n
.
Accordingly, the index is expressed as
ind Q = i
n
d
µ=1
dξ
µ
0
√
2π
dη
µ
0
Det
PBC
−δ
µν
d
dt
+
˜
µν
(x
0
)
−1/2
. (12.186)
Let us evaluate the functional determinant in (12.186). Since the Fermi
variables are contained only in
˜
µν
(x
0
) and this is Grassmann-even, we pretend
this part is a commuting number for the time being. The anti-symmetry of the
Riemann tensor implies that
˜
µν
(x
0
) satisfies
˜
µν
=−
˜
νµ
. Therefore, it is
possible, in an even-dimensional manifold M, to block-diagonalize
˜
µν
in the
form
˜
µν
=
0 y
1
−y
1
0
.
.
.
0 y
n
−y
n
0
. (12.187)
Let us concentrate on the first block. The operator
−δ
µν
d
dt
+
˜
µν
(x
0
)
is real and, hence, the eigenvalues are made of complex conjugate pairs. Let us
express the determinant of this block in terms of the product of these complex
eigenvalues. We find
det
−
d
dt
y
1
−y
1
−
d
dt
= Det
d
2
dt
2
+ y
2
1
=
n=0
y
2
1
− (2πn/β)
2
=
n≥1
2πn
β
2
n≥1
1 −
y
1
β
2πn
2
2
=
sin β y
1
/2
y
1
/2
2
. (12.188)
Now the index is expressed as
ind Q = i
n
2n
µ=1
dξ
µ
0
√
2π
dη
µ
0
n
j =1
y
j
/2
sin β y
j
/2
. (12.189)
The product with respect to j is written as
1
β
d/2
det
β
˜
/2
sin β
˜
/2
1/2
.
Note that any Taylor expansion with respect to
˜
terminates at finite order since
˜
p
= 0for p > d/2.
We have evaluated the contributions of the second-order fluctuations around
a particular pair x
0
,ψ
0
so far. Now we need to take the contributions coming
from all the solutions to the classical equations of motion into account. We have
noted before that the set
of the solutions of the equations of motion contains
the constant solution (x
0
,ψ
0
) as a subset and that the contributions from non-
constant solutions are exponentially small as β ↓ 0. Therefore, we neglect all
periodic solutions except for constant solutions. If we note the expansion
x
µ
= x
µ
0
+
1
√
β
ξ
µ
0
+···
we find that the integral over x
0
is equivalent with that over ξ
0
/
√
β, namely
dx
µ
0
= dξ
µ
0
/
√
β. This argument is also applied to the Grassmannian zero mode
and we find dψ
µ
0
=
√
βdη
µ
0
. In summary, the index is now written as
ind Q = i
n
2n
µ=1
dx
µ
0
√
2π
dψ
µ
0
1
β
d/2
det
β
˜
/2
sin β
˜
/2
1/2
. (12.190)
We make the following change of variables to erase the apparent β-dependence
of the index,
ψ
µ
0
=
χ
µ
0
√
2πβ
, dψ
µ
0
=
2πβ dχ
µ
0
.
Substituting
β
˜
µν
=
1
2π
1
2
µνρσ
χ
ρ
0
χ
σ
0
into the integrand, we obtain
ind Q = i
n
2n
µ=1
dx
µ
0
dχ
µ
0
det
1
2
1
2π
1
2
µνρσ
(x
0
)χ
ρ
0
χ
σ
0
sin
1
2
1
2π
1
2
µνρσ
(x
0
)χ
ρ
0
χ
σ
0
1/2
. (12.191)
This is the Atiyah–Singer index theorem for the Dirac operator.
Let us rewrite the previous theorem in a more familiar form. Note that only
terms of order 2n in χ in the integrand yield non-vanishing contributions upon
integration over
dχ
µ
0
. Note also that
dx
µ
0
is just an ordinary volume element.
Then define the curvature two-form
µν
=
1
2
R
µνρσ
dx
ρ
∧ dx
σ
. (12.192)
Then note that
/ sin is even in and, hence, the integral is non-vanishing
only when n is even, that is only when d is a multiple of four. If this is the case,
the factor i
n
takes only ±1 and we can formally replace the integrand as
i
n
sin
→
sinh
.
The reader should verify the first few terms. Then the index is now written in the
well-known form as
ind Q =
M
det
1
2
1
2π
sinh
1
2
1
2π
1/2
.
We, moreover, define the
ˆ
A-genus. Since
is anti-symmetric, it can be block-

diagonalized as
1
2π
µν
=
0 x
1
−x
1
0
.
.
.
0 x
n
−x
n
0
.
Then define the
ˆ
A-genus of M by
ˆ
A(M) =
n
j =1
x
j
/2
sinh x
j
/2
(12.193)
where the RHS is defined by its formal expansion with respect to x
j
.
In summary, we have proved the Atiyah–Singer index theorem in the
simplest setting (the spin complex).
Theorem 12.6. (Index theorem for a spin complex) The index of a Dirac
operator defined in M is
ind Q =
M
ˆ
A(M). (12.194)
Problems
12.1 In the text, we dealt only with compact manifolds. The extension of the AS
index theorem to non-compact manifolds is the Callias–Bott–Seely index theorem
(Callias 1978, Bott and Seely 1978). Here we consider the simplest case studied
by Hirayama (1983). Consider a pair of operators
L ≡
1
i
d
dx
− iW (x ) L
†
≡
1
i
d
dx
+ iW (x )
where W (+∞) = µ and W (−∞) = λ.
(a) Show that Spec
L
†
L = Spec
LL
†
, where the prime indicates that the zero
eigenvalues are omitted.
(b) Show that
J (z) ≡ tr
z
L
†
L + z
−
z
LL
†
+ z
=
1
2
µ
(µ
2
+ z)
1/2
−
λ
(λ
2
+ z)
1/2
.

13
ANOMALIES IN GAUGE FIELD THEORIES
In particle physics, symmetry principles are some of the most important
concepts in model building. Symmetries play crucial roles for the theory to be
renormalizable and unitary. The Lagrangian must be chosen so that it fulfils
the observed symmetry. Note, however, that the symmetry of the Lagrangian is
classical. There is no warranty that symmetry of the Lagrangian may be elevated
to a quantum symmetry, i.e., the symmetry of the effective action. If the classical
symmetry of the Lagrangian cannot be maintained in the process of quantization,
the theory is said to have an anomaly. There are many types of anomaly: the chiral
anomaly, gauge anomaly, gravitational anomaly, supersymmetry anomaly and so
on. Each adjective refers to the symmetry under consideration. In the present
chapter we look at the geometrical and topological structures of the anomalies
appearing in gauge theories.
We follow closely Alvarez-Gaum´e (1986), Alvarez-Gaum´e and Ginsparg
(1985) and Sumitani (1985). See Rennie (1990) and Bartlmann (1996) for a
complete analysis of the subject. Mickelsson (1989) and Nash (1991) have a
section on anomalies from a more mathematical point of view.
13.1 Introduction
Before we introduce topological and geometrical methods to anomalies, we give
a brief survey of the subject here. Let ψ be a massless Dirac field in four-
dimensional space interacting with an external gauge field
µ
= A
µ
α
T
α
,where
{T
α
} is the set of anti-Hermitian generators of the gauge group G which is
compact and semisimple (SU(N), for example). The theory is described by the
Lagrangian
= i
¯
ψγ
µ
(∂
µ
−
µ
)ψ. (13.1)
The Lagrangian is invariant under the usual (local) gauge transformation
ψ(x) → g
−1
ψ(x)
µ
(x ) → g
−1
[
µ
(x ) + ∂
µ
]g. (13.2)
It also has a global symmetry,
ψ(x) → e
iγ
5
α
ψ(x)
¯
ψ(x ) →
¯
ψ(x )e
iγ
5
α
(13.3)
