Nakahara M. Geometry, Topology and Physics
Подождите немного. Документ загружается.

Let P(S
4
, SU(2)) be the instanton bundle. Expression (12.88) reads as
ν
+
− ν
−
=
S
4
ch
2
( ) =
−1
8π
2
S
4
tr
2
. (12.90)
The RHS represents the instanton number k ∈ π
3
(SU(2)) = . Note that k > 0
if
=∗ while k < 0if =−∗ . It can be shown that ν
−
= 0(ν
+
= 0)
if k > 0(k < 0), see Jackiw and Rebbi (1977). For example, let
be self-dual.
Suppose ψ
−
∈ ker D
†
= ker DD
†
. From (12.80), we find that
DD
†
ψ
−
=[(∂
µ
+
µ
)
2
+ 2i ¯σ
µν
µν
]ψ
−
= 0
where ¯σ
µν
≡ (1/4i)(α
µ
¯α
ν
−α
ν
¯σ
µ
). It is easily verified that ¯σ
µν
is anti-self-dual
( ¯σ
µν
=−∗¯σ
νµ
) and hence ¯σ
µν
µν
= 0. Since (∂
µ
+
µ
)
2
is a positive-definite
operator, it has no normalizable bound states. This verifies that ker D
†
=∅.
12.7 The heat kernel and generalized ζ -functions
As we mentioned in section 12.2, there are several methods of proving the AS
index theorem. The heat kernel is relatively accessible to physicists and it also
has many applications to other problems in physics. The generalized ζ -function
is related to the heat kernel and also has relevance in physics.
12.7.1 The heat kernel and index theorem
Let E be a complex vector bundle over an m-dimensional compact manifold M.
Let : (M, E) → (M, E) be an elliptic operator with eigenvectors |n such
that
|n=λ
n
|n. (12.91)
We denote the set of eigenvalues of by Spec . We assume that is non-
negative, i.e. all the eigenvalues are non-negative. Suppose there are n
0
modes
|0, i , 1 ≤ i ≤ n
0
with vanishing eigenvalue. In other words,
dim ker = n
0
. (12.92)
These modes are called the zero modes.Definetheheat kernel h(t) by
h(t) ≡ e
−t
. (12.93)
It is convenient to represent h(t) in the coordinate basis as
h(x , y;t) ≡x|h(t)|y=x|
n
e
−t
|nn|y
=
n
e
−tλ
n
x |nn|y. (12.94)

12.7 THE HEAT KERNEL AND GENERALIZED ζ -FUNCTIONS 473
Multiple eigenstates should be counted as many times as they appear. We assume
x |n is orthonormal:
n|xx|mdx = δ
mn
. The convergence of (12.93) for
t > 0 is guaranteed since is non-negative. Taking the limit t →∞,wehave
lim
t→∞
h(x , y;t) =
n
0
i=1
x |0, i 0, i|y (12.95)
where the summation is over the zero modes |0, i only. Thus, h = e
−t
tends to
be the projection operator onto the space of zero modes as
e
−t
t→∞
−→
n
0
i=1
|0, i 0, i|. (12.96)
Define
˜
h(t) ≡
h(x , x;t) dx =
n
e
−tλ
n
. (12.97)
Then it follows from (12.95) that
n
0
= lim
t→∞
˜
h(t). (12.98)
It is easy to verify that h satisfies the heat equation,
∂
∂t
+
x
h(x , y;t) = 0. (12.99)
If is the conventional Laplacian, (12.99) reduces to the ordinary heat equation.
The initial condition is
h(x , y;0) =
n
x |nn|y=δ(x − y) (12.100)
where the last equality follows from the completeness of the eigenvectors.
Exercise 12.4. Let u(x , t) be a solution of (12.99) such that u(x, 0) = u(x).Show
that
u(x , t) =
h(x , y;t)u(y) dy. (12.101)
[Hint: First verify that (12.101) satisfies the initial condition, next that it is a
solution of the heat equation.]
It is known that the solution of (12.99) has an asymptotic expansion for
t → ε given by
h(x , x;ε) =
i
a
i
(x )ε
i
(12.102)
see Gilkey (1984). Similarly, h(t) has an expansion
˜
h() ≡
i
a
i
ε
i
(12.103)
where a
i
=
a
i
(x )dx.
Let E and F be complex vector bundles over M and D : (M, E) →
(M, F) be an elliptic operator. We define two Laplacians
E
≡ D
†
D : (M, E) → (M, E) (12.104a)
F
≡ DD
†
: (M, F) → (M, F). (12.104b)
It is important to note that they have the same non-vanishing eigenvalues
including the degeneracy. To see this, let
E
|λ=λ|λ. Then there is a vector
D|λ∈(M, F) such that
F
(D|λ) = DD
†
D|λ=D
E
|λ=λ(D|λ).
Note that D|λ = 0sinceker
E
= ker D.Conversely,if|µ) ∈ (M, F)
satisfies
F
|µ) = µ|µ),thenD
†
|µ) ∈ (M, E) is an eigenvector of
E
with
the same eigenvalue µ. Thus, we have found the symmetry
3
Spec
E
= Spec
F
(12.105)
where the prime denotes that the zero eigenmodes are omitted.
Define two heat kernels h
E
and h
F
by
h
E
(x , y, t) =
e
−λ
n
x |nn|y (12.106a)
h
F
(x , y, t) =
e
−µ
m
x |m)(m|y. (12.106b)
We have
lim
t→∞
˜
h
E
(t) = dim ker
E
= dim ker D (12.107a)
lim
t→∞
˜
h
F
(t) = dim ker
F
= dim ker D
†
. (12.107b)
What is more interesting is the index of D.SincekerD = ker
E
and ker D
†
=
ker
F
,wehave
ind D = dim ker D − dim ker D
†
= dim ker
E
− dim ker
F
= lim
t→∞
[
˜
h
E
(t) −
˜
h
F
(t)]=
˜
h
E
(t) −
˜
h
F
(t). (12.108)
The final equality follows since the t-dependent part of
˜
h
E
(t) −
˜
h
F
(t) cancels out
by the symmetry (12.105). We expand
˜
h
E
(t) and
˜
h
F
(t) as
˜
h
E
(t) =
a
E
i
t
i
˜
h
F
(t) =
a
F
i
t
i
.
3
This is a kind of ‘supersymmetry’, see section 12.10.

12.7 THE HEAT KERNEL AND GENERALIZED ζ -FUNCTIONS 475
Picking up t-independent terms, we have
ind D = a
E
0
− a
F
0
=
dx [a
E
0
(x ) − a
F
0
(x )]dx (12.109)
where a
E,F
0
(x ) are defined in (12.102).
In general, a
E,F
0
(x ) are local invariants written in terms of curvature two-
forms. In section 13.2, we use the heat kernel to prove the index theorem
ind D = ν
+
− ν
−
=
M
ch( )|
vol
for the twisted spin complex over a manifold with
ˆ
A(TM) = 1.
Exercise 12.5. Let D, D
†
,
E
and
F
be as before. Show that
I (s) ≡ tr
s
E
+ s
−
s
F
+ s
Re s > 0 (12.110)
is independent of s. Show also that I (s) = ind D.
12.7.2 Spectral ζ -functions
Let E and F be vector bundles over M. Define a new function
ζ
E
(x , y;s) ≡
x |nn|yλ
−s
n
Re s > 0 (12.111)
where
E
|n=λ
n
|n and the prime denotes the omission of the zero modes
(λ
n
= 0). A function ζ
F
(x , y;s) may similarly be defined for
F
. The functions
h
E
and ζ
E
are related by the Mellin transformation. To see this, we recall the
definition of the -function,
(s) ≡
∞
0
t
s−1
e
−t
dt = λ
s
∞
0
t
s−1
e
−λt
dt
where λ is taken to be strictly positive. From this we find
(s)ζ (x , y;s) =
n
∞
0
t
s−1
e
−λ
n
t
x |nn|ydt
=
∞
0
t
s−1
h(x , y;t) −
i
x |0, i 0, i|y
dt. (12.112)
We also note that
ζ
(s) ≡
M
ζ(x, x;s) dx =
n
λ
−s
n
(12.113)
is the spectral ζ -function defined in (1.158).
Exercise 12.6. Verify that
−s
f (x) =
ζ(x, y;s) f (y) dy (12.114)
where the general power of an operator may be defined in the sense of an
eigenvalue, namely we put
−s
|n=λ
−s
n
|n.Res is assumed to be sufficiently
large so that (12.114) is well defined. [Hint: Use the completeness of the
eigenvectors.]
Example 12.7. The following example is taken from Kulkarni (1975). Let M =
S
1
={e
iθ
} and E = F = a trivial line bundle over S
1
(a cylinder). Take an
operator ≡−∂
2
/∂θ
2
. From the eigenvalue equation,
−
∂
2
e
inθ
∂θ
2
= n
2
e
inθ
n ∈
we find that
λ
n
= n
2
θ|n=(2π)
−1/2
e
inθ
.
The heat kernel is
h(θ
1
,θ
2
;t) =
e
−n
2
t
θ
1
|nn|θ
2
=
1
2π
1 +
e
−n
2
t
e
in(θ
1
−θ
2
)
(12.115)
while
ζ(θ
1
,θ
2
;s) =
n
−2s
θ
1
|nn|θ
2
=
1
2π
n
−2s
e
in(θ
1
−θ
2
)
. (12.116)
We easily verify that
˜
h(t) = 1 +
e
−n
2
t
satisfies
1 +2
∞
1
e
−x
2
t
dx <
˜
h(t)<1 +2
∞
0
e
−x
2
t
dx.
We then find from these inequalities that
+∞
−∞
e
−x
2
t
dx − 1 <
˜
h(t)<
+∞
−∞
e
−x
2
t
dx + 1
or by putting the value
e
−x
2
t
dx =
√
πt
−1/2

we find
√
π t
−1/2
− 1 <
˜
h(t)<
√
πt
−1/2
+ 1.
This shows that
lim
t→0
+
˜
h(t) ∼
√
πt
−1/2
. (12.117)
In general, the asymptotic series starts with t
−dim M/2
.
12.8 The Atiyah–Patodi–Singer index theorem
So far we have been concerned with index theorems defined on a compact
manifold without a boundary. In practical situations in physics, we often need
to find an index of an operator defined over a base space M with a boundary.
The extensions of the AS index theorem to these cases are discussed here. Our
argument is restricted to the spin bundle over M since this is the only situation we
shall be concerned with in chapter 13.
12.8.1 η-invariant and spectral flow
Let i
/
∇ be a Hermitian Dirac operator defined on an odd-dimensional manifold M,
dim M = 2l + 1. Since i
/
∇ is Hermitian, the eigenvalues λ
k
are real. We define
the η-invariant of i
/
∇ by the spectral asymmetry of i
/
∇,
η ≡
λ
k
>0
1 −
λ
k
<0
1. (12.118)
This is not well defined and requires a proper regularization. For example, we
may define η by lim
s→0
η(s) where
η(s) ≡
k
sgn(λ
k
)|λ
k
|
−2s
Re s > 0. (12.119)
It can be shown that, under proper boundary conditions, η(s) has no pole at s = 0.
Exercise 12.7. Use the Mellin transformation
1
2
s + 1
2
a
−(s+1)/2
=
∞
0
dxx
s
e
−ax
2
a > 0
to verify that
η(s) =
2
(
1
2
(s + 1))
∞
0
dxx
s
tr i
/
∇e
−x
2
(i
/
∇)
2
. (12.120)
Suppose a Dirac field is interacting with an external gauge potential
t
, t ∈
[0, 1]. The Dirac operator i
/
∇(
t
) has a t-dependent eigenvalue problem. If
an eigenvalue of i
/
∇(
t
) crosses zero, the η-invariant jumps by ±2. This jump
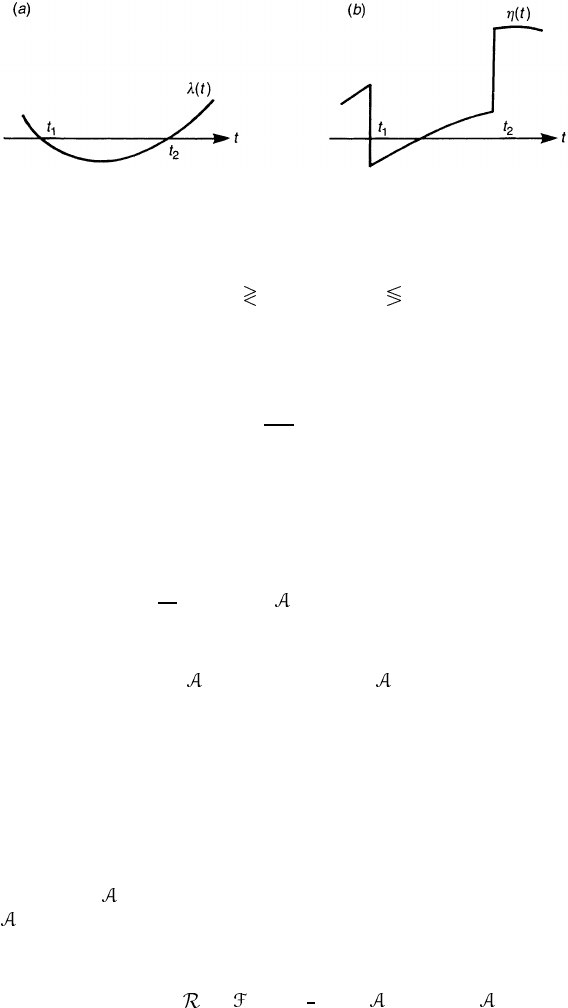
Figure 12.1. Whenever an eigenvalue λ crosses zero (a),theη-invariant jumps by ±2 (b).
The sign depends on the way in which λ crosses zero.
denotes the spectral flow from λ 0 modes to λ 0 modes; if η jumps by
+2 (−2), there is a flow of a state from λ<0toλ>0(λ>0toλ<0), see
figure 12.1. In addition to the discontinuous change associated with the spectral
flow, i
/
∇ also has a continuous variation η
c
.Wehave
η(t = 1) − η(t = 0) =
1
0
dt
dη
c
dt
+ 2 × (spectral flow). (12.121)
12.8.2 The Atiyah–Patodi–Singer (APS) index theorem
Let us consider a (2l + 2)-dimensional Dirac operator
i
ˆ
D
2l+2
= iσ
1
∂
∂t
+ σ
2
⊗ i
/
∇(
t
) =
0 D
D
†
0
(12.122a)
where
D = i∂
t
−
/
∇(
t
) D
†
= i∂
t
+
/
∇(
t
). (12.122b)
[Remark: The positions of D and D
†
are reversed since
γ
2l+3
=
−1 0
0 1
for our choice of γ -matrices; cf (12.79).]
Theorem 12.3. (Atiyah–Patodi–Singer theorem)LetM be an odd-dimensional
manifold and i
/
∇(
t
) a Dirac operator on M interacting with an external gauge
field
t
. Then,
ind D = dim ker D − dim ker D
†
=
M×I
ˆ
A(
)ch( )|
vol
−
1
2
[η(i
/
∇(
1
)) − η(i
/
∇(
0
))].
(12.123)
The general argument shows that the continuous part η
c
of the η-invariant
satisfies
1
0
dt
dη
c
dt
= 2
M×I
ˆ
A(
)ch( )|
vol
. (12.124)
Then the RHS of (12.123) is simply the spectral flow
−
1
2
[η(t = 1) − η(t = 0)]+
1
2
1
0
dt
dη
c
dt
=−spectral flow.
Thus, we find another expression for the APS index theorem,
ind i
ˆ
D
2l+2
=−spectral flow. (12.125)
The proof of the APS index theorem in its most general form is found in Atiyah et
al (1975a, b, 1976). The physicists’ proof is found in Alvarez-Gaum´e et al (1985).
We use the APS index theorem to study the odd-dimensional parity anomaly in
section 13.6.
Example 12.8. To see why the spectral flow appears in the index theorem, we
consider an example taken from Atiyah (1985). Let M = S
1
and θ be its
coordinate. Consider a Hermitian operator
i∇
t
≡ i
∂
∂θ
− it
= i∂
θ
+ tt∈ . (12.126)
The term −it is thought of as a U(1) gauge potential. The eigenvector and the
eigenvalue of i∇
t
are
ψ
n,t
(θ) =
1
√
2π
e
−inθ
(n ∈ )λ
n
(t) = n + t.
Since Spec i∇
t
= Spec i∇
t+1
, the family of operators i∇
t
is periodic in t with the
period 1, see figure 12.2. This periodicity manifests itself in the gauge equivalence
of i∇
t
and i∇
t+1
:
i∇
t+1
= e
iθ
i∇
t
e
−iθ
.
There is precisely unit spectral flow from λ<0toλ>0att = 0 while t changes
from −ε to 1 − ε, ε being a small positive number. From i∇
t
, we construct a
two-dimensional Dirac operator
i
/
D
2
≡ iσ
1
⊗
∂
∂t
+ σ
2
⊗ i∇
t
=
0 D
D
†
0
(12.127a)
where
D ≡ i∂
t
+ ∂
θ
− itD
†
≡ i∂
t
− ∂
θ
+ it.(12.127b)
These operators act on functions which satisfy the boundary conditions
φ(θ + 2π, t) = φ(θ,t)φ(θ,t + 1) = e
iθ
φ(θ,t). (12.128)
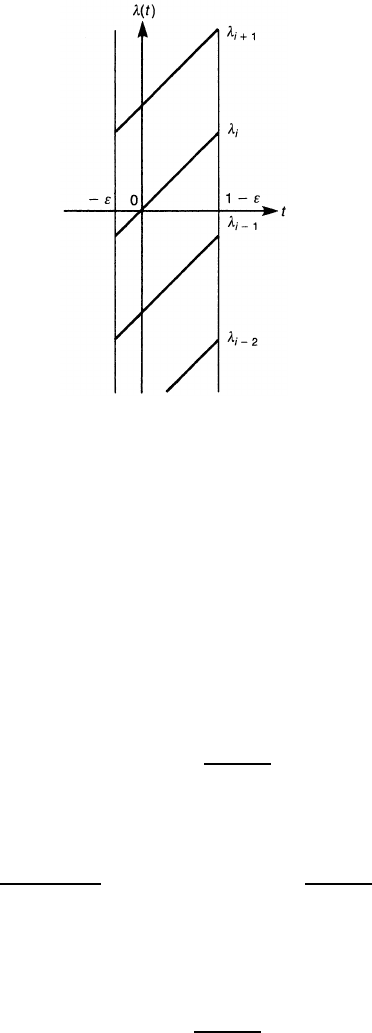
Figure 12.2. Time evolution of the eigenvalues of i∇
t
.Speci∇
t
has period 1. The ith
eigenvalue crosses zero at t = 0 and, hence, there is a unit spectral flow.
Let φ
0
∈ ker D
†
. We have a Fourier expansion
φ
0
(θ, t) =
a
n
(t)e
−inθ
.
It follows from D
†
φ
0
= 0that
a
n
(t) + (n + t)a
n
(t) = 0
which is easily solved to yield
a
n
(t) = c
n
exp
−
(n + t)
2
2
.
The boundary conditions (12.128) require that
n
c
n
exp
−
(n + t + 1)
2
2
e
−inθ
=
n
c
n
exp
−
(n + t)
2
2
e
−i(n−1)θ
from which we find that c
n
is independent of n. Thus, ker D
†
is one dimensional
and is spanned by the theta function,
φ
0
(θ, t) =
exp
−
(n + t)
2
2
− inθ
. (12.129)

Suppose
˜
φ
0
(θ, t) ∈ ker D. If we put
˜
φ
0
(θ, t) =
b
n
(t)e
−inθ
, b
n
(t) satisfies
b
n
(t) − (n + t)b
n
(t) = 0.
The solution of this equation is
b
n
(t) = b
n
(0) exp
(n + t)
2
2
and, hence,
˜
φ
0
cannot be normalized. This shows that
ind D = dim ker D − dim ker D
†
=−1
which agrees with −(spectral flow).
12.9 Supersymmetric quantum mechanics
We present, in the next section, the physicists’ proof of the index theorem in
its simplest setting. The proof is heavily based on path integral formulation of
supersymmetric quantum mechanics (SUSYQM), which will be outlined in the
present section.
We have studied the path integral quantization of bosons and fermions.
If these particles are combined together, there appears a new symmetry called
supersymmetry. We will introduce a special class of SUSYQM later, which
turns out to be crucial in the proof of an index theorem.
This and the next sections may be read separately from the previous sections.
The necessary tools are supplied to make these sections self-contained. Our
exposition follows Alvarez (1995) and Nakahara (1998). Original references are
Alvarez-Gaum´e L (1983) and Friedan and Windey (1984, 1985).
12.9.1 Clifford algebra and fermions
We restrict ourselves to a particle moving in
3
to start with. More general
settings will be studied later. Let {ψ
i
}={ψ
1
,ψ
2
,ψ
3
} be real Grassmann
variables, where i = 1, 2, 3 labels the coordinate index. They satisfy the algebra
{ψ
i
,ψ
j
}=0
Let us consider the Lagrangian
L =
i
2
ψ
i
˙
ψ
i
−
i
2
ijk
B
i
ψ
j
ψ
k
(12.130)
where B
i
is a real number. The canonical conjugate momentum for ψ
i
is
π
i
≡
∂ L
∂
˙
ψ
i
=−
i
2
ψ
i
.
