Nakahara M. Geometry, Topology and Physics
Подождите немного. Документ загружается.


13.4 The Wess–Zumino consistency conditions
13.4.1 The Becchi–Rouet–Stora operator and the Faddeev–Popov ghost
Let W [
] be the effective action of the Weyl fermion in the complex
representation r of the gauge group G.
3
In the previous section, we observed that
the change of W [
] under an infinitesimal gauge transformation δ
v
=− v is
given by
δ
v
W [ ]=−
(
µ
v)
α
δ
δ
µ
α
W [ ]=
v
α
µ
j
µ
α
. (13.58)
Following Stora (1984) and Zumino (1985) we introduce the BRS operator
and the Faddeev–Popov ghost ω.Let
m
(G) be the set of maps from S
m
to G.
4
In addition to the ordinary exterior derivative d, we introduce another exterior
derivative
on
m
(G) which we call the Becchi–Rouet–Stora (BRS) operator.
In general,
is defined on an infinite-dimensional space but we may also consider
the restriction of
to a finite-dimensional compact subspace of
m
(G),suchas
S
n
, parametrized by λ
α
.Then may be written as ≡ dλ
α
∂/∂λ
α
. We require
that d and
be anti-derivatives,
d
2
=
2
= d + d = 0. (13.59)
If we define ≡ d +
, is clearly nilpotent,
2
= d
2
+ d + d +
2
= 0. (13.60)
Under the action of g = g(x ,λ
α
), transforms as
→ A ≡ g
−1
( + d)g. (13.61)
Note that
is independent of λ while A depends on λ through g.Definethe
Faddeev–Popov (FP) ghost by
ω ≡ g
−1
g. (13.62)
The actions of
on A and ω are found to be
A = [g
−1
( + d)g]=−g
−1
g A − g
−1
g + g
−1
(dg)
=−ω A − ( A− g
−1
dg)ω − g
−1
d( g)
=−ω A − Aω − dω ≡−
A
ω (13.63a)
ω =−g
−1
gg
−1
g =−ω
2
. (13.63b)
3
We drop the representation index r to simplify the expression.
4
The set
m
(G) should not be confused with
m
(M),thesetofm-forms on M. The distinction
should be clear from the context.

It is easy to verify that
is nilpotent on A and ω and, hence, on any polynomial
of A and ω as it should be; see exercise 13.1. Define the field strength of A by
F ≡ d A + A
2
= g
−1
g. (13.64)
We also define
≡ g
−1
( + )g = A + g
−1
g = A + ω (13.65a)
≡ +
2
= g
−1
g = F (13.65b)
where (13.65b) follows since
= d +
2
= +
2
(note that = 0). It
is found from theorem 10.1 that
is an Ehresmann connection on the principal
bundle and
its associated curvature two-form.
The existence of a non-Abelian anomaly implies that W [A] does not vanish
under the action of the BRS operator
(ω roughly corresponds to v; see (13.39)
and (13.63a)),
W [A]=G[ω, A]. (13.66)
Since W [A] is independent of ω,
acts through A only. Before we write down
the Wess–Zumino consistency condition for the non-Abelian anomaly, we stop
here and consider the physical meaning of the BRS operator and the FP ghost.
Exercise 13.1. Verify from (13.63) that the actions of
on A and ω are nilpotent,
2
A = 0
2
ω = 0. (13.67)
13.4.2 The BRS operator, FP ghost and moduli space
To find the physical meaning of
and ω, we need to examine the topology of
the gauge fields (Atiyah and Jones 1978, Singer 1985, Sumitani 1985). Let
be the space of all gauge potential configurations on S
m
. For definiteness, we
take m = 4 but the generalization to arbitrary m is obvious. The topology
of
is trivial since, for any gauge potential configurations
1
and
2
,the
combination t
1
+ (1 − t)
2
(0 ≤ t ≤ 1) is again a gauge potential on S
4
.
Note, however, that
does not describe the physical configuration space of the
gauge theory. We have to identify those field configurations which are connected
by G-gauge transformations. Let
be the space of all gauge transformations on
S
4
( =
4
(G) in our previous notation). Then the physical configuration space
must be identified with
/ , called the moduli space of the gauge theory. We
have seen in section 10.5 that the gauge field configuration on S
4
is classified by
the transition function g : S
3
→ G, S
3
being the equator of S
4
. In the present
case,
/ is classified by the transition function on the equator S
3
→ G and,
hence,
/
3
(G). (13.68)
Thus, each connected component of
/ is labelled by the instanton number k.
This component is denoted by
4
k
(G).
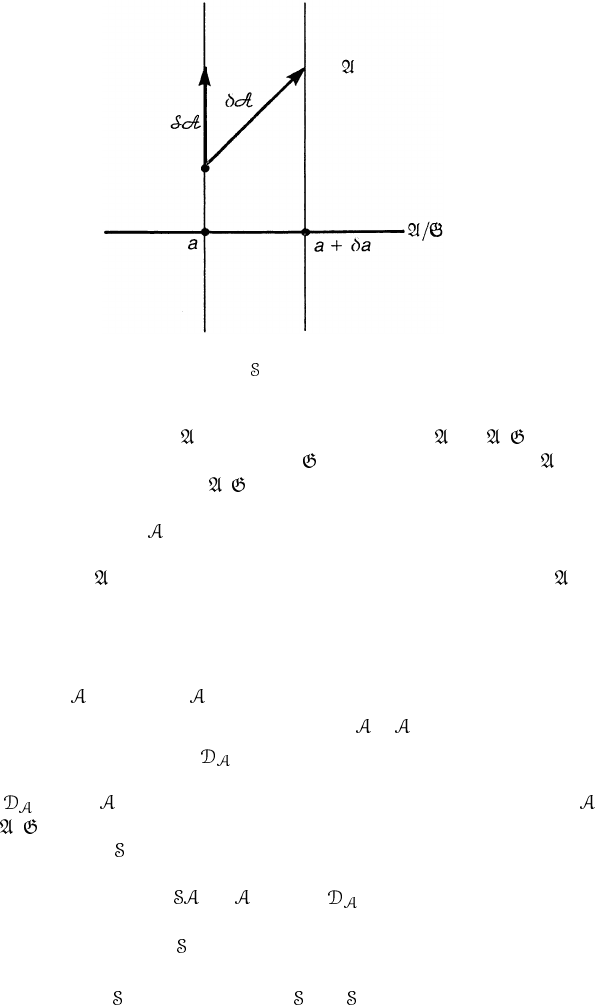
Figure 13.1. The BRS operator is the restriction of δ along the fibre.
We note that the space has a natural projection π : → / and can
be made into a fibre bundle whose fibre is
, see figure 13.1. Let a ∈ be a
representative of the class [a]∈
/ and let
(x ) = g
−1
(x )(a(x) + d)g(x ) (13.69)
be an element of
in [a]. We denote the exterior derivative operator in by
δ,whichisafunctional variation and should not be confused with the usual
derivative d; see Leinaas and Olaussen (1982). If δ is applied on (13.69), we
find that
δ
=−g
−1
δg + g
−1
δag − g
−1
aδg − g
−1
d (δg)
= g
−1
δag − d (g
−1
δg) − g
−1
δg − g
−1
δg
= g
−1
δag − (g
−1
δg) (13.70)
where
= d +[ , ]. The first term of (13.70) represents the derivative of
along / while the second represents that along the fibre; see figure 13.1. The
BRS transformation
is obtained by restricting the variation δ along the fibre,
≡ δ |
fibre
=− ω (13.71a)
where the FP ghost ω is g
−1
g ≡ g
−1
δg
fibre
. We also find that
ω = δω|
fibre
=−g
−1
gg
−1
g =−ω
2
(13.71b)
which reproduces (13.63a).
13.4.3 The Wess–Zumino conditions
Exercise 13.1 shows that
is nilpotent on any polynomial f of and ω,
2
f (ω, A) = 0. (13.72)
The nilpotency is required by the interpretation of
as an exterior derivative
operator. In particular, we should have
G[ω, A]=
2
W [A]=0. (13.73)
This condition is called the Wess–Zumino consistency condition (WZ
condition) and can be used to determine the non-Abelian anomaly (Wess and
Zumino 1971, Stora 1984, Zumino 1985, Zumino et al 1984). If the anomaly G is
mathematically well defined, G should satisfy the WZ condition. This condition
is so strong that once the first term of G[ω, A] is given, the anomaly is completely
pinned down.
13.4.4 Descent equations and solutions of WZ conditions
Stora (1984) and Zumino (1985) constructed the solution of WZ conditions as
follows. The Abelian anomaly in (2l + 2)-dimensional space is given by
ch
l+1
(F) =
1
(l + 1)!
tr
iF
2π
l+1
(13.74)
where F = d A + A
2
, A = g
−1
( + d)g as before. Let Q
2l+1
( A, F) be the
Chern–Simons form of ch
l+1
(F),
ch
l+1
(F) = dQ
2l+1
( A, F). (13.75)
Since the algebraic structure of the triplet (,
, ) is exactly the same as that of
(d, A, F),wealsohave
ch
l+1
( ) = Q
2l+1
( , ) = Q
2l+1
( A + ω, F) (13.76)
where we have noted that
= A + ω and = F. If we expand Q
2l+1
( , ) =
Q
2l+1
( A+ ω, F) in powers of ω,wehave
Q
2l+1
( , ) = Q
0
2l+1
( A, F) + Q
1
2l
(ω, A, F) + Q
2
2l−1
(ω, A, F)
+···+Q
2l+1
0
(ω, A, F) (13.77)
where Q
s
r
is sth order in ω and r + s = 2l + 1.
We now note that ch
l+1
( ) = ch
l+1
(F) since = F = g
−1
g.Intermsof
the Chern–Simons forms, this can be expressed as
Q
2l+1
( , ) = dQ
2l+1
( A, F). (13.78)

Substituting (13.77) into (13.78), we have
(d +
)[Q
0
2l+1
( A, F) + Q
1
2l
(ω, A, F)
+···+Q
2l+1
0
(ω, A, F)]=dQ
0
2l+1
( A, F). (13.79)
If we collect terms of the same order in ω,wehavethe‘descent equations’
Q
0
2l+1
( A, F) + dQ
1
2l
(ω, A, F) = 0 (13.80a)
Q
1
2l
(ω, A, F) + dQ
2
2l−1
(ω, A, F) = 0 (13.80b)
.
.
.
Q
2l
1
(ω, A, F) + dQ
2l+1
0
(ω, A, F) = 0 (13.80c)
Q
2l+1
0
(ω, A, F) = 0. (13.80d)
Note here that
increases the degree of ω by one, see (13.63). Let us look at the
2l-form Q
1
2l
(ω, A, F). If we put
G[ω, A, F]≡
M
Q
1
2l
(ω, A, F) (13.81)
G[ω, A, F] satisfies the WZ condition,
G[ω, A, F]=
M
Q
1
2l
(ω, A, F) =−
M
dQ
2
2l−1
(ω, A, F)
=−
∂ M
Q
2
2l−1
(ω, A, F) = 0
wherewehaveassumedthatM has no boundary and use has been made
of (13.80b). This shows that once Q
1
2l
(ω, A, F) is obtained, the anomaly
G[ω, A, F] is easily found.
Proposition 13.1. Q
1
2l
defined here is given by
Q
1
2l
(ω, , ) =
i
2π
l+1
1
(l − 1)!
1
0
δt (1 − t) str[ωd(
l−1
t
)]. (13.82)
[Note: In the proof, we tentatively drop the normalization factor (i/2π)
l+1
to
simplify the expressions. This factor will be recovered at the very end.]
Proof. We start with (11.105),
Q
2l+1
( + ω, ) =
1
l!
1
0
δt tr[( + ω)
ˆ
l
t
]
where
ˆ
t
≡ t + (t
2
− t)( + ω)
2
=
t
+ (t
2
− t){ ,ω}+(t
2
− t)ω
2
t
≡ d (t ) + (t )
2
.
If we substitute
ˆ
t
into Q
2l+1
and collect terms of first order in ω,wehave:
1
l!
1
0
δt tr[ω
l
t
+ (t
2
− t)( [ ,ω]
l−1
t
+
t
[ ,ω]
l−2
t
+···+
l−1
t
[ ,ω])]
=
1
l!
δt str[ω
l
t
+ (t
2
− t) (
l−1
t
[ ,ω]]
+
l−2
t
[ ,ω]
t
+···)]
=
1
l!
δt str[ω
l
t
+ (t
2
− t)l [ ,v]
l−1
t
]
=
1
l!
δt str[ω
l
t
+l(t
2
− t)([ , ]ω
l−1
t
+ ω[ ,
l−1
t
])]
=
1
l!
δt str[ω{
l
t
+l(t − 1)(t[ , ]
l−1
t
− [
t
,
l−1
t
])}]
where str is the symmetrized trace defined by (11.8). Now we use
t
l−1
t
≡ d
l−1
t
+[
t
,
l−1
t
]=0
∂
t
∂t
= d
+ t[ , ]
to change the final line of the previous equation to
1
l!
δt str
ω
l
t
+l(t − 1)
∂
t
∂t
− d
l−1
t
+ d
l−1
t
=
1
l!
δt str
ω
l
t
+l(1 −t)d(
l−1
t
) + (t − 1)
∂
l
t
∂t
.
Integrating by parts, we find that
Q
1
2l
(ω, , ) =
1
(l − 1)!
δt (1 − t) str[ωd(
l−1
t
)].
If we recover the normalization, we finally have
Q
1
2l
(ω, , ) =
i
2π
l+1
1
(l − 1)!
1
0
δt (1 − t) str[ωd(
l−1
t
)].

For m = 2l = 2andm = 4, we have
Q
1
2
(ω, A, F) =
i
2π
2
tr(ωd A) (13.83a)
Q
1
4
(ω, A, F) =
1
6
i
2π
3
str(ωd( Ad A +
1
2
A
3
)). (13.83b)
These results are also verified by direct computations. Up to the normalization
factor, (13.83b) yields the non-Abelian anomaly in four-dimensional space; see
(13.56).
Sumitani (1984) pointed out that the approach to the non-Abelian anomalies
here is ad hoc and does not clarify the following points:
(1) The WZ condition (13.73) does not fix the normalization of the anomaly and,
moreover, the uniqueness of the solution is far from trivial.
(2) It is not clear why we should start from the Abelian anomaly in (m + 2)-
dimensional space.
To answer these questions we need to develop a more elaborate index
theorem called the family index theorem; see Atiyah and Singer (1984), Singer
(1985) and Sumitani (1984, 1985). In the next section, we outline the physicists’
approach to this problem, closely following the work of Alvarez-Gaum´eand
Ginsparg (1984).
13.5 Abelian anomalies versus non-Abelian anomalies
Let us consider an m-dimensional Euclidean space (m = 2l)whichis
compactified to S
m
=
m
∪{∞}and let G be a semisimple gauge group which
is simply connected (like SU(N) for which π
1
(SU(N)) is trivial). Consider a
one-parameter family of gauge transformations g(θ, x )(0 ≤ θ ≤ 2π) such that
g(0, x) = g(2π, x) = e. (13.84)
Without loss of generality, we may normalize g so that g(θ, x
0
) = e at a point
x
0
∈ S
m
.Themapg : S
1
×S
m
→ G is classified according to the homotopy class
π
m+1
(G). To see this we define the smash product X ∧ Y of topological spaces
X and Y by the direct product X × Y with X ∨ Y ≡ (x
0
× X) ∪ (X × y
0
) shrunk
to a point. From figure 13.2, we easily find that S
1
∧ S
m
= S
m
∧ S
1
= S
m+1
.
5
Repeated applications of this yield
S
m
∧ S
n
= S
m+n
. (13.85)
In the case which interests us, the conditions (13.84) make the direct product
S
1
× S
m
look topologically like S
1
∧ S
m
= S
m+1
. Thus, g is regarded as a map
5
The readers may convince themselves by explicitly drawing S
1
∧ S
1
= S
2
.
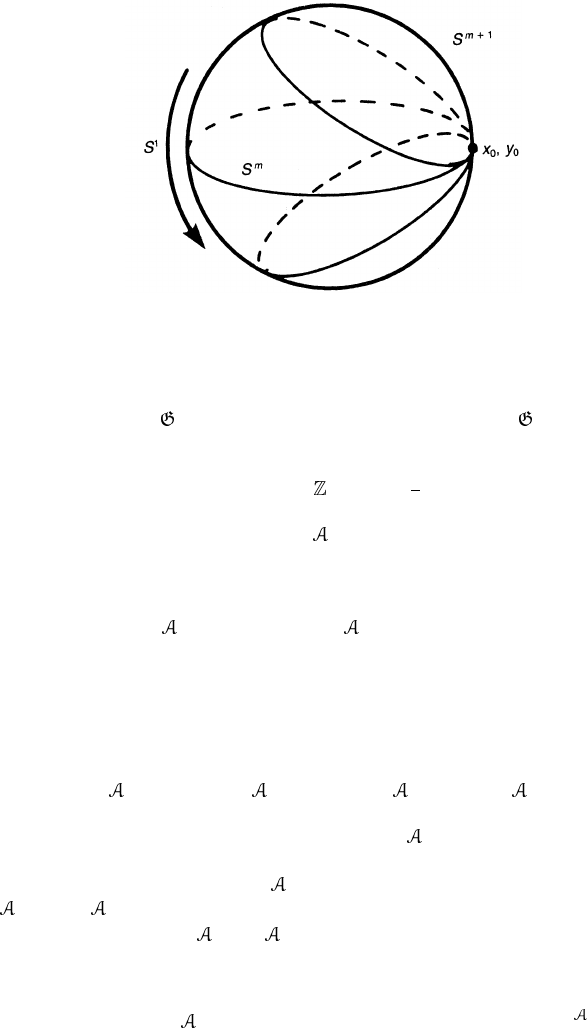
Figure 13.2. The smash product S
1
∧ S
m
S
m+1
.
from S
m+1
to G and is classified by π
m+1
(G). Since we have a one-parameter
family in the space
=
m
(G),wealsohaveπ
m+1
(G) = π
1
( ). In practice,
we take G = SU(N) for which we have
π
m+1
(SU(N)) = N ≥
1
2
m + 1. (13.86)
Now we take a ‘reference’ gauge field
in the zero instanton sector
m
0
(G) for
which we may assume, without loss of generality, that the Dirac operator (13.49)
has no zero modes. Consider a one-parameter family of gauge potentials
g(θ)
(x ) ≡ g
−1
(θ, x )( (x ) + d)g(θ, x ) (13.87)
where θ parametrizes S
1
. In section 13.3, we observed that |det i
ˆ
D| is gauge
invariant (see (13.47)) and only the phase of det i
ˆ
D maygainananomalous
variation under a gauge transformation. This, in particular, implies that det i
ˆ
D
does not vanish for any θ. We write
exp{−W
r
[
g(θ)
]} = det i
ˆ
D(
g(θ)
) =[det i
/
∇( )]
1/2
exp[iw( ,θ)] (13.88)
where i
/
∇ is the Dirac operator (13.49) and exp[iw(
,θ)] is the anomalous phase
associated with the gauge transformation (13.87). Next we consider a two-
parameter family of gauge fields
t,θ
(0 ≤ t ≤ 1) which interpolates between
= 0and
g(θ)
,
t,θ
≡ t
g(θ)
(0 ≤ t ≤ 1). (13.89)
The parameter space specified by (t,θ)is considered to be a two-dimensional unit
disc D
2
with polar coordinates (t,θ). On the boundary of the disc, ∂ D
2
= S
1
,
the modulus of det i
ˆ
D(
1,θ
) is a non-vanishing constant. The phase e
iw( ,θ)
now
defines a map S
1
(=∂ D
2
) → S
1
(=U(1)); see figure 13.3. As we move around
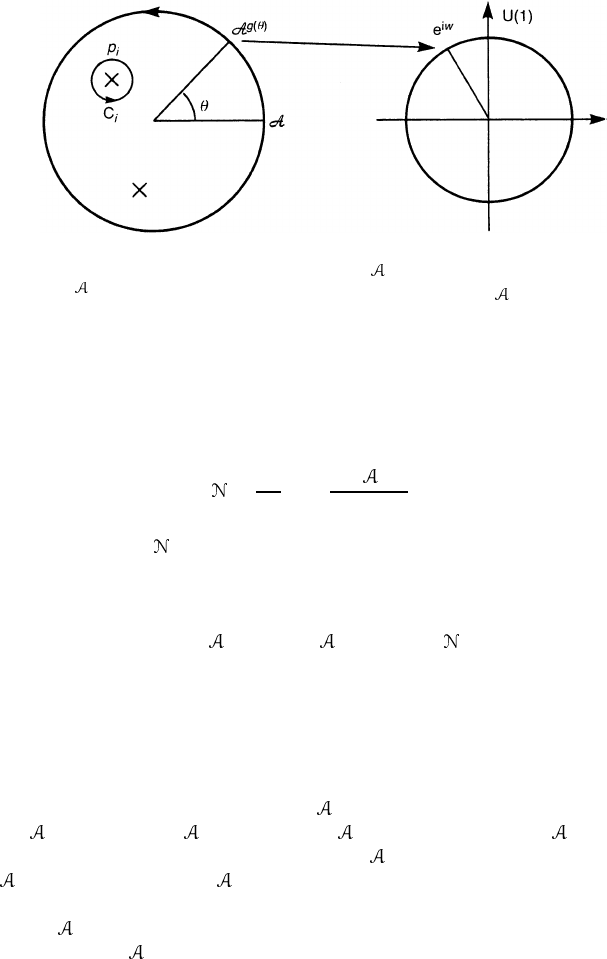
Figure 13.3. The phase of the effective action W [
g(θ)
] defines a map S
1
→ U(1) by
θ → e
iw( ,θ)
. On the disc, there are points {p
i
} at which det i
ˆ
D(
t,θ
) vanishes. The
winding number of the map S
1
→ U(1) is obtained by summing a winding number along
C
i
.
the boundary of the disc, the phase winds around the unit circle. The winding
number of this map is an integer
=
1
2π
2π
0
∂w( ,θ)
∂θ
dθ. (13.90)
We find below that
is derived from the Abelian anomaly in (m +2) dimensions.
Exercise 13.2. Show that
W [
g(2π)
]−W [
g(0)
]=−2πi . (13.91)
Since g(2π) = g(0), (13.91) may be regarded as a Berry phase.
13.5.1 m dimensions versus m + 2dimensions
We recall that our reference gauge field
supports no zero modes of the operator
i
ˆ
D(
).Since|det i
ˆ
D(
g(θ)
)|=|det i
ˆ
D( )| = 0, the operator i
ˆ
D(
g(θ)
) does
not admit zero modes either. Of course, i
ˆ
D(
t,θ
) may have zero modes since
t,θ
is not obtained from by a gauge transformation in general. Suppose it
has a zero mode at p
i
= (t
i
,θ
i
). We assume they are isolated points. Since
det i
ˆ
D(
t,θ
) is a regularized product of eigenvalues, it vanishes at p
i
.The
phase of det i
ˆ
D(
t,θ
) may be homotopically non-trivial only around these points.
Moreover, the winding number at p
i
is determined by the eigenvalue which
vanishes at p
i
. For example, if λ
n
(t,θ)vanishes at p
i
it should be of the form
λ
n
(t,θ) = f (t,θ)e
iw
i
(t,θ)
(13.92)
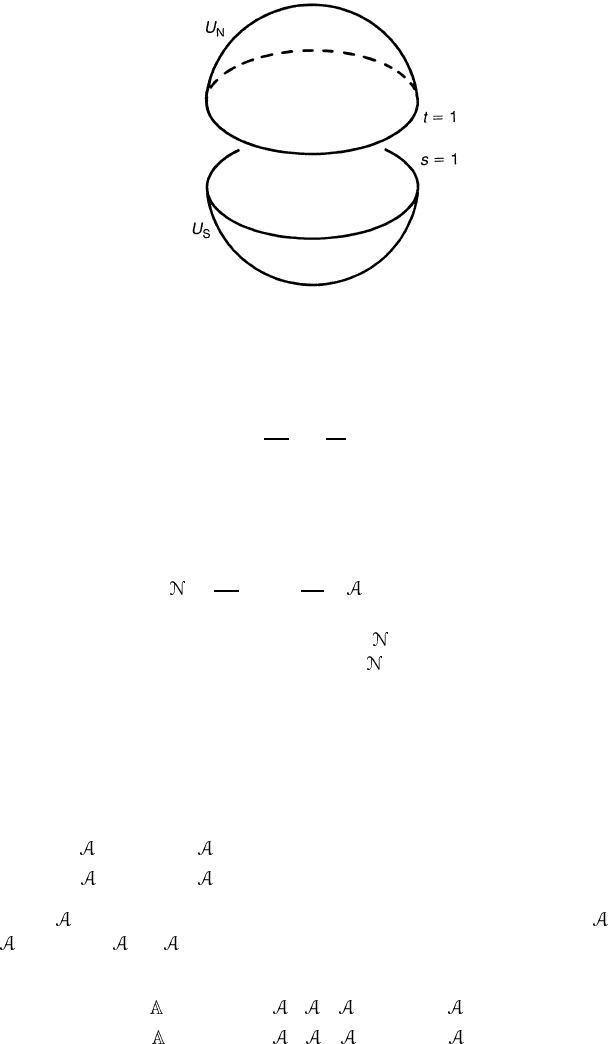
Figure 13.4.
where f (t
i
,θ
i
) = 0. The winding number at p
i
is
m
i
=
1
2π
C
i
d
ds
w
i
(t,θ)ds (13.93)
where C
i
is a small contour surrounding p
i
, see figure 13.3. Continuously
deforming the loop S
1
= ∂ D
2
into a sum of small circles C
i
enclosing p
i
,we
find that the total winding number is
=
1
2π
S
1
dθ
∂
∂θ
w(
,θ) =
m
i
. (13.94)
Now we show that the winding number
is related to the index theorem
in (m + 2)-dimensional space (m = 2l):
= ind i
/
∇
m+2
where i
/
∇
m+2
is
the Dirac operator on S
2
× S
m
defined later. Let us consider a gauge theory
defined on D
2
× S
m
whose coordinates are (t,θ,x ). To avoid the boundary term,
we add another piece, D
2
× S
m
, with coordinates (s,θ,x ), to form a manifold
S
2
×S
m
without a boundary; see figure 13.4. We call the patch (t,θ)the northern
hemisphere U
N
and (s,θ) the southern hemisphere U
S
. On the equator S
1
of S
2
,
we have t = s = 1. We choose the following local gauge potentials
N
(t,θ,x) =
t,θ
+ g
−1
d
θ
g (t,θ)∈ U
N
(13.95a)
S
(s,θ,x ) = (s,θ) ∈ U
S
(13.95b)
where
is the reference gauge field introduced previously. To elevate
N
=
Nµ
dx
µ
and
S
=
Sµ
dx
µ
to the globally defined connection on the G bundle
over S
2
× S
m
we define the (m + 2)-dimensional gauge potentials
N
(t,θ,x ) = (
t
,
θ
,
µ
) = (0, 0,
Nµ
) (13.96a)
S
(s,θ,x ) = (
s
,
θ
,
µ
) = (0, 0,
Sµ
). (13.96b)
