Nakahara M. Geometry, Topology and Physics

Подождите немного. Документ загружается.

called the chiral symmetry. The chiral current j

derived from this symmetry is

≡

ψγ

ψ. (13.4)

In general, whether the symmetry of a Lagrangian is retained under quantization

is not a trivial question. In fact, it has been shown that the chiral symmetry of

is destroyed at the quantum level. Adler (1969) and Bell and Jackiw (1969) have

shown by computing the triangle diagram with an external axial current and two

external vector currents that the naive conservation law ∂

= 0 is violated,

∂

16π



κλµν

κλ µν

4π





κλµν

∂



∂

µ ν

λ µ ν



(13.5)

where tr is a trace over the group indices. The current j

which appears in (13.5)

has no group index, and, hence, (13.5) is called the Abelian anomaly.

It is interesting to study the behaviour of a current which carries the group

index. Consider a Weyl fermion ψ which couples with an external gauge

ﬁeld. The non-Abelian gauge current of the theory also satisﬁes an anomalous

conservation law which deﬁnes the non-Abelian anomaly. The action is given

≡ ψ

†

∇)

(I ± γ

). (13.6)

The Lagrangian has the gauge symmetry

→ g

−1

(

+ ∂

)g ψ → g

−1

ψ. (13.7)

The corresponding non-Abelian current is

µα

≡ ψ

†

ψ. (13.8)

It has been shown by Bardeen (1969) and Gross and Jackiw (1972) that, up to the

one-loop level, the current is not conserved,

(

)

24π



∂



κλµν



∂

µ ν

λ µ ν



. (13.9)

At ﬁrst sight, the RHSs of (13.5) and (13.9) look very similar. However, the

difference between the normalization and the numerical factors of

and

have

a deep topological origin. We shall see later that the Abelian anomaly in (2l + 2)

dimensions and the non-Abelian anomaly in 2l dimensions are closely related but

in an unexpected manner.

13.2 Abelian anomalies

Henceforth, we work in an even-dimensional manifold M (dim M = m = 2l)

with a Euclidean signature. Four-dimensional results will readily be obtained by

putting m = 4. We assume our system is non-chiral, namely, the gauge ﬁeld

couples to the right and the left components in the same way. Our convention is

µ†

= γ

{γ

,γ

}=2δ

µν

m+1

= (i)

...γ

m+1†

= γ

m+1

(γ

m+1

)

=+I.

The Lie group generators {T

} satisfy

†

=−T

, T

]= f

αβ

tr(T

) =−

αβ

13.2.1 Fujikawa’s method

Among several methods of deriving anomalies, Fujikawa’s way (Fujikawa 1979,

1980, 1986) reveals the topological and geometrical nature of the problem most

directly. This method is equivalent to the heat kernel proof of the relevant index

theorem.

Let ψ be a massless Dirac ﬁeld interacting with an external non-Abelian

gauge ﬁeld

. The effective action W [ ] is given by

−W [ ]



ψ e

−



ψi

∇ψ

(13.10)

where i

∇=iγ

∇

= iγ

(∂

+ ω

), with ω

µαβ



αβ

being the

spin connection of the background space. We compactify the space in such a

way that the geometry (the spin connection) plays no role. For example, this

can be achieved by compactifying

to S

∪{∞}, for which the Dirac

genus

A(TM) is trivial; see example 12.5. If this is the case, the spin connection

is irrelevant and may be dropped from i

∇. The classical action



ψi

∇ψ is

invariant with respect to the chiral rotation,

ψ → e

iγ

m+1

ψ →

ψe

iγ

m+1

. (13.11)

We expand ψ and

ψ as

ψ =



ψ =



†

(13.12)

where a

and

are anti-commuting Grassmann variables,

, a

}=0 {

}=0 {a

}=0

and ψ

is an eigenvector of the Dirac operator

∇ψ

= λ

. (13.13)

Since i

∇ is Hermitian, λ

is real. Since M is compact, ψ

can be normalized as

ψ

|ψ

=



dxψ

†

(x )ψ

(x ) = δ

Now the path integrals over ψ and

ψ are replaced by those over a

and

Consider an inﬁnitesimal chiral transformation,

ψ(x) → ψ(x) + iα(x)γ

m+1

ψ(x) (13.14a)

ψ(x ) →

ψ(x ) + i

ψ(x )α(x)γ

m+1

. (13.14b)

As usual, we take α = α(x) to be x-dependent. Under this change, the classical

action transforms as



ψi

∇ψ →



dx (

ψ + i

ψαγ

m+1

∇(ψ + iαγ

m+1

ψ)



ψi

∇ψ + i



dx [α

ψγ

m+1

∇ψ +

ψi

∇(αγ

m+1

ψ)]



ψi

∇ψ −



dx [α

ψγ

m+1

(∂

)ψ

ψγ

(∂

)(αγ

m+1

ψ)]



ψi

∇ψ +



dx α(x)∂

m+1

(x ) (13.15)

where we have used the anti-commutation relations {γ

,γ

m+1

}=0and

m+1

(x ) ≡

ψ(x)γ

m+1

ψ(x) (13.16)

is the chiral current. This is the higher-dimensional analogue of j

deﬁned

previously. If (13.15) were the only change caused by (13.14), naive application

of the Ward–Takahashi relation would imply the conservation of the axial current

∂

m+1

= 0. In quantum theory, however, we have an additional change, namely

the change of the path integral measure. Deﬁne the chiral-rotated ﬁelds by



= ψ + iαγ

m+1

ψ =





(13.17a)



ψ + i

ψαγ

m+1





†

. (13.17b)

Now the measure changes as





→







. (13.18)

From the orthonormality of {ψ

},weﬁndthat



=ψ

|ψ



=ψ

|(1 +iαγ

m+1

)ψ



ψ

|(1 + iαγ

m+1

)ψ

a

≡



(13.19a)

where

=ψ

|(1 +iαγ

m+1

)ψ

=δ

+ iαψ

|γ

m+1

. (13.20)

The measure in terms of the new variables is





=[det C

]

−1



= exp(−tr ln C

)



= exp[−tr ln(I + iαψ

|γ

m+1

)]



≈ exp(−tr iαψ

|γ

m+1

)



= exp



− iα



ψ

|γ

m+1







(13.21)

where the inverse of the determinant appears since a

and a



are Grassmann

variables, see Berezin (1966).

As for

→



,wehave





ψ

|(1 +iαγ

m+1

)|ψ

=



.(13.19b)

The Jacobian for the change

→



agrees with (13.21). Thus, the measure

transforms under the chiral rotation (13.17) as



→





exp



− 2i



dx α(x)



†

(x )γ

m+1

(x )



(13.22)

Now the effective action has two expressions:

−W [ ]





exp



−



ψi

∇ψ









exp



−



ψi

∇ψ −



dx α(x)∂

m+1

(x )

− 2i



dx α(x) A(x)



(13.23)

where

A(x) ≡



†

(x )γ

m+1

(x ). (13.24)

Since α(x) is arbitrary, we have

∂

m+1

(x ) =−2i A(x ). (13.25)

See section 1.5. For example, we have



a da =



ca d(ca) = 1, c ∈ and a being a real

Grassmann number. This shows that d(ca) = da/c.

Thus, naive conservation of an axial current does not hold in quantum theory.

This non-conservation of the current j

m+1

is called the Abelian anomaly (or

chiral anomaly or axial anomaly).

How is this related to the topology? Let us look at the Jacobian (13.22)

and assume that α(x) is independent of x.

The integral in (13.22) is not well

deﬁned and must be regularized. We introduce the Gaussian cut-off (heat kernel

regularization) as



dx A(x) =





†

(x )γ

m+1

(x ) exp[−(λ

/M)

M→∞



ψ

|γ

m+1

exp[−(i

∇/M)

]|ψ

|

M→∞

. (13.26)

In (13.26), 1/M

corresponds to the ‘time’ parameter t in the previous chapter

and M →∞implies t → ε.Let|ψ

 be an eigenstate of i

∇ with non-vanishing

eigenvalue λ

. Among the eigenstates, there exists a state |ψ



≡ γ

m+1

|ψ with

eigenvalue −λ

∇|ψ



= i

∇γ

m+1

|ψ

=−γ

m+1

∇|ψ



=−λ

m+1

|ψ

=−λ

|ψ



where use has been made of the anti-commutation relation {γ

m+1

, i

∇}= 0. Since

∇ is a Hermitian operator, eigenvectors which belong to different eigenvalues are

orthogonal, hence ψ

|ψ



=ψ

|γ

m+1

|ψ

=0. This shows that

ψ

|γ

m+1

exp[−(i

∇/M)

]|ψ

=ψ

|γ

m+1

|ψ

exp[−(λ

/M)

]=0.

Thus, the contribution to the RHS of (13.26) comes only from the zero-energy

modes. Let |0, i  be the zero-energy modes of i

∇, (1 ≤ i ≤ n

).Theyare

not in an irreducible representation of the spin algebra and should be classiﬁed

according to the eigenvalue of γ

m+1

. We write

m+1

|0, i 

=±|0, i 

. (13.27)

Then, (13.26) becomes



dx A(x) =



ψ

|γ

m+1

exp[−(i

∇/M)

]|ψ

|

M→∞



0, i |0, i

−



−

0, i |0, i

−

= ν

− ν

−

= ind i

∇

(13.28)

where ν

(ν

−

) is the number of zero-energy modes with positive (negative)

chirality (ν

+ ν

−

= n

)andi

∇

is deﬁned by

∇=



∇

−

∇



∇

−

= (i

∇

)

†

We are looking at the zero-momentum Ward–Takahashi relation.

The Atiyah–Singer index theorem now comes into the problem.

To show that (13.28), indeed, represents an integral of the relevant Chern

character, we ﬁrst note that

∇)

=−γ

∇

=−{δ

µν

[γ

,γ

]}

[{∇

, ∇

µν

]

=−∇

∇

−

[γ

,γ

]

µν

(13.29)

where use has been made of the relation [∇

, ∇

µν

.Then

A(x) =



ψ

|xx|γ

m+1

exp[(∇

[γ

,γ

]

µν

)/M

]|ψ

|

M→∞

. (13.30)

Let us take m = 4 for deﬁniteness. We introduce the plane wave basis as

x |ψ

=



(2π)

x |kk|ψ

.

Then (13.30) becomes

A(x) =



(2π)



(2π)



ψ



k



|x

× γ

m+1

exp[(∇

[γ

,γ

]

µν

)/M

]x |kk|ψ





M→∞

y→x



(2π)

tr γ

m+1

exp[(−k

[γ

,γ

]

µν

)/M

]

M→∞

(13.31)

where use has been made of the completeness property



k|ψ

ψ



=(2π)

(k − k



In (13.31), we have replaced ∇

by the symbol −k

since the residual terms

containing

do not survive in the limit M →∞. If we put

≡ k

/M,

(13.31) becomes

A(x) = tr[γ

exp(

[γ

,γ

]

µν

)]M



(2π)

exp(−

We expand the ﬁrst exponential and use

tr γ

= tr γ

= 0trγ

=−4

κλµν



k exp(−

) = π

to obtain

A(x) =



{[γ

,γ

]

µν

}



16π

−1

32π

tr 

κλµν

κλ

(x )

µν

(x ). (13.32)

Note that the higher-order terms in the expansion of the exponential vanish in the

limit M →∞. The anomalous conservation law (13.25) now becomes

∂

16π

tr 

κλµν

κλ µν

4π

tr[

κλµν

∂

(

∂

µ ν

λ µ ν

)]. (13.33)

This is regarded as a local version of the AS index theorem. Let us write (13.33)

in terms of the ﬁeld strength

µν

∧ dx

. We easily verify that

− ν

−



dx ∂

m+1



( ). (13.34)

This is the index theorem for a twisted spinor complex with trivial background

geometry (

A(TM) = 1).

For dim M = m = 2l, we have the following identity:

− ν

−



dx ∂

m+1



( ) =





2π



. (13.35)

13.3 Non-Abelian anomalies

In the last section we considered the chiral current which is a gauge singlet (no

gauge indices). Now we turn to the study of the gauge current j

where α is the

gauge index. Here we consider a chiral theory in which the gauge ﬁeld

couples

only to the left-handed Weyl fermion ψ. Suppose ψ transforms in a complex

representation r of the gauge group G. For example, suppose ψ belongs to a 3 of

SU(3). The effective action W

[ ] is given by

−W

[ ]



ψ exp



−



ψi

∇



(13.36)

where

∇

= iγ

(∂

)

+ ±

(1 ± γ

m+1

). (13.37)

The gauge current is

= i

ψγ

α +

ψ. (13.38)

Let v = v

be an inﬁnitesimal gauge transformation parameter, g = 1 − v

under which we have

→ (1 + v)(

+ d)(1 −v) =

−

v (13.39)

where

v ≡ ∂

v +[

,v] is the covariant derivative for a ﬁeld in the adjoint

representation. The effective action transforms as

[ ]→W

[ − v]

= W

[ ]−



dx tr



[ ]



= W

[ ]−



dx tr(∂

+ f

αβγ

)

δ A

[ ]

= W

[ ]+



dx tr



[ ]



. (13.40)

Since

δ A

[ ]=i

ψγ

(1 + γ

m+1

)ψ =j



we obtain

[ − v]−W

[ ]=



dx tr(v

j



). (13.41)

We are naively tempted to regard (13.36) as det(i

∇) =





, λ

being the

‘eigenvalue’ of i

∇. A subtlety arises here: i

∇

maps sections of S

⊗ E to those

of S

−

⊗ E,whereE is the vector bundle associated with the G bundle and S

are spin bundles with chirality ±. Accordingly, the equation i

∇

ψ = λψ is

meaningless. To avoid this difﬁculty, we formally introduce a Dirac spinor ψ and

deﬁne

−W

[ ]



ψ exp



−



ψi

Dψ



(13.42)

where i

D is deﬁned by

D ≡ iγ

(∂

+ i

µ +

) =



∂

−

∇



(13.43)

where we have diagonalized γ

m+1

. In (13.43), the gauge ﬁeld couples only

to the positive chirality ﬁeld. Now the eigenvalue problem i

Dψ

= λ

is well

deﬁned. Note that i

D is not Hermitian and λ

is a complex number in general.

Moreover, we need to introduce right and left eigenfunctions separately by

Dψ

= λ

(13.44a)

†

←

D) = λ

†

. (13.44b)

Since



†

dx = 0fori = j , we may choose an orthonormal basis,



†

dx = δ

. (13.45)

It should be noted that the eigenvalue λ

is not gauge invariant. This follows from

the observation that

g(i

))g

−1

= giγ

[∂

+ g

−1

(

+ ∂

−1

= i

D( ) − i

∂gg

−1

+ i

∂gg

−1

= i

D( ). (13.46)

If the equality were to hold in (13.46), g

−1

would satisfy i

−1

when i

D( )ψ

= λ

. Then Spec i

D( ) would be gauge invariant.

Although individual eigenvalues are not gauge invariant, the absolute value of the

product of eigenvalues of i

D is gauge invariant. In fact,

det(i

D) det((i

†

) = det(i

D(i

†

)

= det



∂

−

)(i

∂

) 0

0 (i

∇

)(i

∇

−

)



= det(i

∂

−

∂

) det(i

∇

−

) (13.47)

where i

∂

= (i

∂

−

)

†

and i

∇

−

= (i

∇

)

†

. This is simply the Dirac determinant

(up to an irrelevant factor det(i

∂

−

∂

)),

[det(i

∇)]

= det



∇

−

∇

−



=[det(i

∇

−

)]

(13.48)

where i

∇ is given by

∇=



∇

−

∇



. (13.49)

The Dirac determinant is gauge invariant, hence so is |det(i

D)|. It then follows

that Re W

[ ] is gauge invariant since

exp(−W

[ ]) exp(−W

[ ]) = det(i

D) det((i

†

) ∝ det(i

∇

−

)

is gauge invariant. Therefore, only the imaginary part of W

[ ], that is the phase

of det(i

D), may gain an anomalous variation under gauge transformations.

The anomaly may be computed by evaluating the Jacobian as before. The

functional measure is taken to be



. We consider an inﬁnitesimal gauge

transformation,

→ − vψ→ ψ + vψ

ψ →

ψ −

−

v (13.50)

where the gauge transformation rotates the positive chirality parts only. The

Jacobian factor is



dx tr v(x)



(n|x γ

m+1

x |n (13.51)

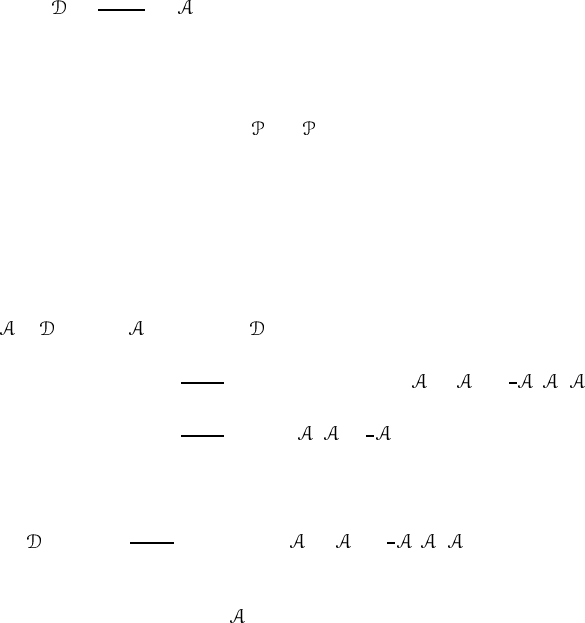
where x |n=ψ

(x ) and (n|x =χ

†

(x ) (note that (n| is not the Hermitian

conjugate of |n). This integral is ill deﬁned and must be regularized. As before,

we employ the Gaussian regulator,



dx lim

M→∞

x→y

tr v(x)



(n|yγ

m+1

x |e

−(i

|n



dx lim

M→∞

x→y

tr v(x)γ

m+1

−(i

)

δ(x − y) (13.52)

where use has been made of the completeness relation



|n(n|=I. (13.53)

It follows from (13.41) and (13.52) that



dx v



δ A

[ ]





dx lim

M→∞

x→y

tr[vγ

m+1

−(i

)

δ(x − y)].

(13.54)

In the present case W

really changes under (13.50). The trace may be written as

tr[vγ

m+1

−(i

)

]=tr[v(

−

−(i∂

−

i∇

)−(i∇

−

i∂

)/M

]

= tr[v P

(i∂i∇)/M

]−tr[v P

−

(i∇i∂)/M

]. (13.55)

(13.55) can be evaluated in the plane wave basis, which is straightforward but

tedious (see Gross and Jackiw (1972), for example). We derive the non-Abelian

anomaly from a topological viewpoint in the next section. For m = 4, the

anomalous variation is

[ − v]−W

[ ]=



dx v

j



24π



dx tr{v



κλµν

∂

[

∂

µ ν

λ µ ν

]}

24π



tr{vd[

d +

]}. (13.56)

The anomalous divergence of the gauge current is

j



24π

tr{T



κλµν

∂

[

∂

µ ν

λ µ ν

]}. (13.57)

This should be compared with (13.33). There are two differences between these

results: the two-thirds in front of

is replaced by a half and the overall factor is

different.