Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers
Подождите немного. Документ загружается.


6.11 Uniform Convergence, Differentiation, and Integration 211
C =
π
2
12
.
Therefore, by integrating the Fourier series of f (x)=x in (−π, π), we
obtain the Fourier series expansion for the function f (x)=x
2
as
x
2
=4
π
2
12
−
∞
k=1
(−1)
k+1
cos kx
k
2
=
π
2
3
+4
∞
k=1
(−1)
k
k
2
cos kx. (6.11.5)
Obviously,
a
0
2
=
π
2
3
and a
k
=
4(−1)
k
k
2
.
Substituting these results into the Parseval relation (6.5.10) gives
2π
4
9
+16
∞
k=1
1
k
4
=
1
π
π
−π
x
4
dx =
2
5
π
4
.
This leads to another well-known numerical series
∞
k=1
1
k
4
=
π
4
90
. (6.11.6)
Example 6.11.3. (Parseval’s relation for the cosine Fourier series) If
f (x) is continuous with continuous derivatives in 0 ≤ x ≤ π with f
′
(0) =
0=f
′
(π), and its cosine Fourier series
f (x) ∼
1
2
a
0
+
∞
k=1
a
k
cos kx (6.11.7)
converges uniformly in 0 ≤ x ≤ π,andg (x) is p iecewise continuous on
[0,π] with its Fourier cosine series given by
g (x) ∼
1
2
b
0
+
∞
k=1
b
k
cos kx, (6.11.8)
then the following Parseval relation holds
1
π
π
0
f (x) g (x) dx =
1
4
a
0
b
0
+
1
2
∞
k=1
a
k
b
k
. (6.11.9)
It f ollows from the assumptions that term-by-term integration holds. Thus,
π
0
f (x) g (x) dx =
π
0
1
2
a
0
+
∞
k=1
a
k
cos kx
g (x) dx
=
1
2
a
0
π
0
g (x) dx +
∞
k=1
a
k
π
0
g (x)coskx dx
=
π
4
a
0
b
0
+
π
2
∞
k=1
a
k
b
k
.

212 6 Fourier Series and Integrals with Applications
This gives the desired relation (6.11.9). An argument similar to this example
yields the Parseval relation for the Fourier sine series in 0 ≤ x ≤ π
1
π
π
0
f (x) g (x) dx =
1
2
∞
k=1
b
k
β
k
, (6.11.10)
where b
k
and β
k
are the Fourier coefficients involved in the Fourier sine
series of f (x)andg (x) respectively with f
′
(0) = 0 = f
′
(π).
6.12 Double Fourier Series
The theory of Fourier series expansions for functions of two variables is
analogous to that of Fourier series expansions for functions of one variable.
Here we shall present a short description of double Fourier series.
We have seen earlier that, if f (x) is piecewise continuous and periodic
with period 2π, then the Fourier series
f (x) ∼
a
0
2
+
∞
m=1
(a
m
cos mx + b
m
sin mx) ,
converges in the mean to f (x). If f is continuously differentiable, then its
Fourier series converges uniformly.
For the sake of simplicity and convenience, let us consider the func-
tion f (x, y) which is continuously differentiable (a stronger condition than
necessary). Let f (x, y) be periodic with period 2π,thatis,
f (x +2π, y)=f (x, y +2π)=f (x, y) .
Then, if we hold y fixed, we can expand f (x, y) in a uniformly convergent
Fourier series
f (x, y)=
a
0
(y)
2
+
∞
m=1
[a
m
(y)cosmx + b
m
(y)sinmx] (6.12.1)
in which the coefficients are functions of y,namely,
a
m
(y)=
1
π
π
−π
f (x, y)cosmx dx,
b
m
(y)=
1
π
π
−π
f (x, y)sinmx dx.
These coefficients are continuously differentiable in y, and therefore, we can
expand them in uniformly convergent series

6.12 Double Fourier Series 213
a
m
(y)=
a
m0
2
+
∞
n=1
(a
mn
cos ny + b
mn
sin ny) ,
(6.12.2)
b
m
(y)=
c
m0
2
+
∞
n=1
(c
mn
cos ny + d
mn
sin ny) ,
where
a
mn
=
1
π
2
π
−π
π
−π
f (x, y)cosmx cos ny dx dy,
b
mn
=
1
π
2
π
−π
π
−π
f (x, y)cosmx sin ny dx dy,
(6.12.3)
c
mn
=
1
π
2
π
−π
π
−π
f (x, y)sinmx cos ny dx dy,
d
mn
=
1
π
2
π
−π
π
−π
f (x, y)sinmx sin ny dx dy.
Substitution of a
m
and b
m
into equation (6.12.1) yields
f (x, y)=
a
00
4
+
1
2
∞
n=1
(a
0n
cos ny + b
0n
sin ny)
+
1
2
∞
m=1
(a
m0
cos mx + c
m0
sin mx)
+
∞
m=1
∞
n=1
(a
mn
cos mx cos ny + b
mn
cos mx sin ny
+ c
mn
sin mx cos ny + d
mn
sin mx sin ny) . (6.12.4)
This is called the double Fourier series for f (x, y).
(a) When f (−x, y)=f (x, y)andf (x, −y)=f (x, y), all the coefficients
vanish except a
mn
, and the double Fourier series r educes to
f (x, y)=
∞
m=1
∞
n=1
a
mn
cos mx cos ny, (6.12.5)
where
a
mn
=
4
π
2
π
0
π
0
f (x, y)cosmx cos ny dx dy.
(b) When f (−x, y)=f (x, y)andf (x, −y)=−f (x, y), we have

214 6 Fourier Series and Integrals with Applications
f (x, y)=
1
π
2
∞
n=1
b
0n
sin ny +
∞
m=1
∞
n=1
b
mn
cos mx sin ny, (6.12.6)
where
b
mn
=
4
π
2
π
0
π
0
f (x, y)cosmx sin ny dx dy.
(c) When f (−x, y)=−f (x, y)andf (x, −y)=f (x, y), we have
f (x, y)=
1
2
∞
m=1
c
m0
sin mx +
∞
m=1
∞
n=1
c
mn
sin mx cos ny, (6.12.7)
where
c
mn
=
4
π
2
π
0
π
0
f (x, y)sinmx cos ny dx dy.
(d) When f (−x, y)=−f (x, y)andf (x, −y)=−f (x, y), we have
f (x, y)=
∞
m=1
∞
n=1
d
mn
sin mx sin ny, (6.12.8)
where
d
mn
=
4
π
2
π
0
π
0
f (x, y)sinmx sin ny dx dy.
Example 6.12.1. Expand the function f (x , y)=xy into double Fourier se-
ries in the interval −π<x<π, π<y<π.
Since f (−x, y)=−xy = −f (x, y)andf (x, −y)=−xy = −f (x, y), we
find
d
mn
=
4
π
2
π
0
π
0
xy sin mx sin ny dx dy =(−1)
(m+n)
4
mn
.
Thus, the double Fourier series for f in −π<x<π, π<y<πis
f (x, y)=4
∞
m=1
∞
n=1
(−1)
m+n
sin mx sin ny
mn
.
6.13 Fourier Integrals
In earlier sections of this chapter, we have described Fourier series for func-
tions which are periodic with period 2π in the interval (−∞, ∞). However,
functions which are n ot periodic cannot be represented by Fourier series.
6.13 Fourier Integrals 215
In many problems of physical interest, it is desirable to develop an integral
representation for such a fu nction that is analogous to a Fourier series.
We have seen in Section 6.9 that the Fourier series for f (x)inthe
interval [−l,l] is represented by
f (x)=
a
0
2
+
∞
k=1
a
k
cos
kπx
l
+ b
k
sin
kπx
l
, (6.13.1)
where
a
k
=
1
l
l
−l
f (t)cos
kπt
l
dt, k =0, 1, 2,..., (6.13.2)
b
k
=
1
l
l
−l
f (t)sin
kπt
l
dt, k =1, 2, 3,.... (6.13.3)
Substituting (6.13.2) and (6.13.3) into (6.13.1), we have
f (x)=
1
2l
l
−l
f (t) dt +
1
l
∞
k=1
l
−l
f (t)cos
kπt
l
· cos
kπx
l
dt
+
l
−l
f (t)sin
kπt
l
· sin
kπx
l
dt
=
1
2l
l
−l
f (t) dt +
1
l
∞
k=1
l
−l
f (t)cos
kπ
l
(t − x)
dt. (6.13.4)
Suppose that f (x) is absolutely integrable, that is,
∞
−∞
|f (x)|dx
converges. Then,
|a
0
|
2
=
1
2l
l
−l
f (t) dt
≤
1
2l
∞
−∞
|f (t)|dt
which approaches zero as l →∞. Thus, holding x fixed, as l approaches
infinity, equation (6.13.4) becomes
f (x) = lim
l→∞
1
l
∞
k=1
l
−l
f (t)cos
kπ
l
(t − x)
dt.
Now let
α
k
=
kπ
l
,δα=(α
k+1
− α
k
)=
π
l
.
216 6 Fourier Series and Integrals with Applications
Then, the function f (x) can be written as
f (x) = lim
l→∞
∞
k=1
F (α
k
) δα,
where
F (α)=
1
π
l
−l
f (t) cos [α (t − x)] dt.
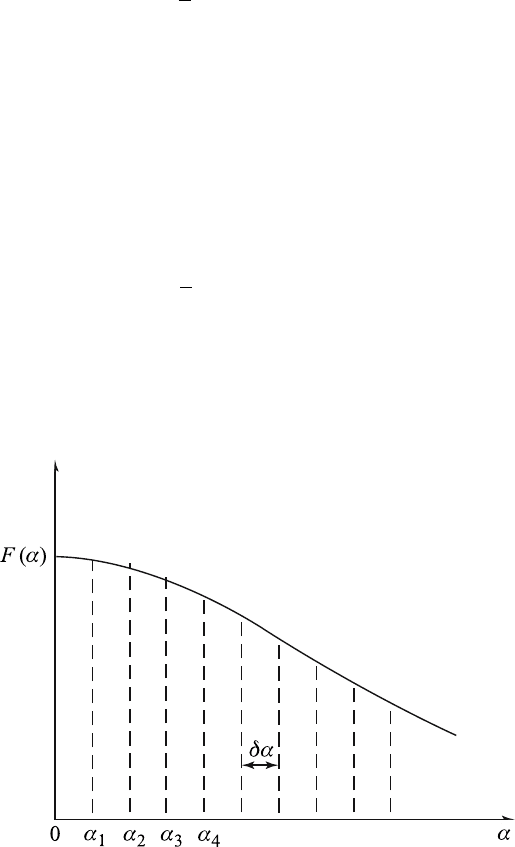
If we plot F (α) against α, we can clearly see that the sum
∞
k=1
F (α
k
) δα
is an approximation to the area under the curve y = F (α) (see Figure
6.13.1). As l →∞and δα → 0 the infinite sum formally approaches the
definite integral. We therefore have
f (x)=
∞
0
1
π
∞
−∞
f (t) cos [α (t − x)] dt
dα (6.13.5)
which is the Fourier integral representation for the function f (x). Its con-
vergence to f (x) is suggested, but by no means established by the preceding
arguments. We shall now prove that this representation is indeed valid if
f (x) satisfies certain conditions.
Figure 6.13.1 Area under the curve F (α).
6.13 Fourier Integrals 217
Lemma 6.13.1. If f is piecewise smooth in the interval [0,b], then for
b>0,
lim
λ→∞
b
0
f (x)
sin λx
x
dx =
π
2
f (0+) .
Proof.
b
0
f (x)
sin λx
x
dx =
b
0
f (0+)
sin λx
x
dx +
b
0
f (x) − f (0+)
x
sin λx dx
= f (0+)
λb
0
sin t
t
dt +
b
0
f (x) − f (0+)
x
sin λx dx.
Since f is piecewise smooth, the integrand of the last integral is bounded
as λ →∞, and thus, by the Riemann–Lebesgue lemma 6.10.1, the last
integral tends to zero as λ →∞. Hence,
lim
λ→∞
b
0
f (x)
sin λx
x
dx =
π
2
f (0+) , (6.13.6)
since
∞
0
sin t
t
dt =
π
2
.
Theorem 6.13.1. (Fourier Integral Theorem) If f is piecewise smooth
in every finite interval, and absolutely integrable on (−∞, ∞), then
1
π
∞
0
∞
−∞
f (t)cosk (t − x) dt
dk =
1
2
[f (x+) + f (x−)] .
Proof. Noting that |cos k (t − x)|≤1 and that by hypothesis
∞
−∞
f (t) dt < ∞,
we see that the integral
∞
−∞
f (t)cosk (t − x) dt
converges independently of k and x. It therefore follows that in the double
integral
I =
λ
0
∞
−∞
f (t)cosk (t − x) dt
dk,
the order of integration may be interchanged. We then have
218 6 Fourier Series and Integrals with Applications
I =
∞
−∞
f (t)
λ
0
cos k (t − x) dk
dt
=
∞
−∞
f (t)
sin λ (t − x)
(t − x)
dt
=
−M
−∞
+
x
−M
+
M
x
+
∞
M
f (t)
sin λ (t − x)
(t − x)
dt.
If we substitute u = t − x,wehave
M
x
f (t)
sin λ (t − x)
(t − x)
dt =
M−x
0
f (u + x)
sin λu
u
du
which is equal to πf (x+) /2 in the limit λ →∞, by Lemma 6.13.1. Simi-
larly, the second integral tends to πf (x−) /2whenλ →∞. If we make M
sufficiently large, the absolute values of the first and the last integrals are
each less than ε/2. Consequently, as λ →∞
∞
0
∞
−∞
f (t)cosk (t − x) dt
dk =
π
2
[f (x+) + f (x−)] . (6.13.7)
If f is continuous at the point x,then
f (x+) = f (x−)=f (x)
so that integral (6.13.7) reduces to the Fourier integral representation for
f as
f (x)=
1
π
∞
0
∞
−∞
f (t)cosk (t − x) dt
dk. (6.13.8)
We may express the Fourier integral representation (6.13.8) in complex
form. In this case, we substitute
cos k (t − x)=cosk (x − t)=
1
2
"
e
ik(x−t)
+ e
−ik(x−t)
#
into equation (6.13.8) and write it as the sum of two integrals
f (x)=
1
2π
∞
0
∞
−∞
f (t) e
ik(x−t)
dt dk +
1
2π
∞
0
∞
−∞
f (t) e
−ik(x−t)
dt dk.
Changing the integration variable from k to −k in the second integral, we
obtain
f (x)=
1
2π
∞
0
∞
−∞
f (t) e
ik(x−t)
dt dk −
−∞
0
∞
−∞
f (t) e
ik(x−t)
dt dk
=
1
2π
∞
0
∞
−∞
f (t) e
ik(x−t)
dt dk +
0
−∞
∞
−∞
f (t) e
ik(x−t)
dt dk
=
1
2π
∞
−∞
∞
−∞
f (t) e
ik(x−t)
dt dk. (6.13.9)
6.13 Fourier Integrals 219
Or, equivalently,
f (x)=
1
√
2π
∞
−∞
e
ikx
dk
1
√
2π
∞
−∞
e
−ikt
f (t) dt
=
1
√
2π
∞
−∞
F (k) e
ikx
dk, (6.13.10)
where
F (k)=
1
√
2π
∞
−∞
e
−ikt
f (t) dt. (6.13.11)
Either (6.13.9) or (6.13.10) with coefficient F (k) is called the complex form
of the Fourier integral representation for f (x).
Now we assume that f (x) is either an even or an odd function. Any
function that is not even or odd can be expressed as a sum of two such
functions. Expanding the cosine function in (6.13.8), we obtain the Fourier
cosine formula
f (x)=f (−x)=
2
π
∞
0
cos kx dk
∞
0
cos kt f (t) dt. (6.13.12)
Similarly, for an odd function, we obtain the Fourier sine formula
f (x)=−f (−x)=
2
π
∞
0
sin kx dk
∞
0
sin kt f (t) dt. (6.13.13)
Example 6.13.1. The rectangular pulse can be expressed as a sum of Heav-
iside functions
f (x)=H (x +1)− H (x − 1) .
Find its Fourier integral representation.
From (6.13.5) we find
f (x)=
1
π
∞
0
1
−1
cos [ k (t − x)] dt
dk
=
1
π
∞
0
cos kx
1
−1
cos kt dt +sinkx
1
−1
sin kt dt
dk
=
2
π
∞
0
sin k
k
cos kx dk.
Example 6.13.2. Find the Fourier cosine integral representation of th e f un c-
tion
f (x)=
⎧
⎨
⎩
1, 0 <x<1,
0,x≥ 1.

220 6 Fourier Series and Integrals with Applications
We have, from (6.13.12),
f (x)=
2
π
∞
0
cos kx dk
1
0
cos kt dt =
2
π
∞
0
sin k
k
cos kx dk,
or,
1=
2
π
∞
0
sin k
k
cos kx dk.
6.14 Exercises
1. Find the Fourier series of the following functions:
(a) f (x)=
⎧
⎨
⎩
x
h
−π<x<0
0 <x<π,
h is a constant
(b) f (x)=
⎧
⎨
⎩
1
x
2
−π<x<0
0 <x<π,
(c) f (x)=x +sinx −π<x<π,
(d) f (x)=1+x −π<x<π,
(e) f (x)=e
x
−π<x<π,
(f) f (x)=1+x + x
2
−π<x<π.
2. Determine the Fourier sine series of the following functions:
(a) f (x)=π − x 0 <x<π,
(b) f (x)=
⎧
⎨
⎩
1
2
0 <x<π/2
π/2 <x<π,
(c) f (x)=x
2
0 <x<π,
(d) f (x)=cosx 0 <x<π,
(e) f (x)=x
3
0 <x<π,
(f) f (x)=e
x
0 <x<π.
